АНАЛИЗ ПРОЧНОСТНЫХ СВОЙСТВ ХАОТИЧЕСКИ АРМИРОВАННОГО КОМПОЗИТА НА ОСНОВЕ МНОГОУРОВНЕВОГО ПОДХОДА
Советова Ю.В.1, Сидоренко Ю.Н.2
1Аспирант; 2Кандидат физ.-мат. наук, доцент, Томский государственный университет
АНАЛИЗ ПРОЧНОСТНЫХ СВОЙСТВ ХАОТИЧЕСКИ АРМИРОВАННОГО КОМПОЗИТА НА ОСНОВЕ МНОГОУРОВНЕВОГО ПОДХОДА
Аннотация
В данной работе решается задача напряженно-деформированного состояния хаотически армированного композита; анализ механического поведения модельного объема материала проведен на основе многоуровневых представлений; прочностные свойства исследованы с использованием кластерного анализа в рамках теории перколяции.
Ключевые слова: многоуровневый подход, кластерный анализ, порог перколяции, соединительный кластер.
Sovetova Y.S.1, Sidorenko Yu.N.2
1Postgraduate student; 2Candidate of physical and mathematical sciences, associate Professor, Tomsk state University
ANALYSIS OF STRENGTH PROPERTIES CHAOTICALLY REINFORCED COMPOSITE BASED ON A LAYERED APPROACH
Abstract
In this work the problem of stress-strain state of chaotically reinforced composite; analysis of the mechanical behavior of the model in the volume of material carried out on the basis of multilevel views; strength properties are investigated with the use of cluster analysis in the framework of the theory of percolation.
Keywords: layered approach, cluster analysis, the threshold of percolation, cluster interconnect.
В настоящее время при производстве самых разных изделий все более широкое применение находят композиционные материалы. Требования к обеспечению надежности и безопасности эксплуатации изделий из композитов обуславливают необходимость учета максимально полной информации о свойствах и особенностях механического поведения композитов как в процессе производства этих материалов, так и при проектировании изделий из них. Cохраняет свою актуальность необходимость развития методов компьютерного моделирования композитов, способных обеспечить максимально полный учет всех факторов и процессов, оказывающих влияние на формирование их механических свойств.
Одной из основных задач вычислительной механики композитов является разработка методов определения эффективных свойств этих материалов. Одним из условий обеспечения корректности вычислительной процедуры определения эффективных свойств материала является требование моделирования его представительного объема. Хаотический характер структуры армирования реальных композитов значительно осложняет выполнение этого требования. Одной из причин осложнений является то, что представительный объем хаотически армированного композита должен включать в себя достаточно большое количество армирующих элементов, что делает крайне проблематичным прямое численное моделирование поведения такого объема вследствие большого объема данных. Другой проблемой является определение критериев выбора размеров объема, обладающего свойством представительности. Для решения данной задачи могут быть предложены различные подходы, в том числе основанные на использовании принципа локальности формирования механических свойств композитов [1].
Одной из наиболее важных механических характеристик любого материала является его прочность. Особенностью этих процессов является то, что они проявляются на разных масштабных уровнях композитов. Для повышения качества результатов численного прогнозирования прочностных свойств композита желательно иметь возможность в процессе моделирования учитывать условия реализации всех подобных процессов для разных масштабных уровней, а также наличие взаимосвязей между процессами, относящихся к разным масштабным уровням.
Одним из возможных способов решения указанных проблем при численном исследовании прочностных свойств хаотически армированных композитов является использование многоуровневых представлений при их моделировании. В данной работе для описания свойств материалов и реализующихся в них процессов используются три масштабных уровня.
Начальным уровнем описания («базовый» уровень - уровень элементарных свойств) является уровень элементарных объемов, полностью принадлежащих одному из компонентов композита. Для оценки прочности таких объемов используется критерий Цая-Ву. Нарушение критерия прочности в элементарном объеме рассматривается как единичный акт повреждения материала компонента композита, результатом которого является снижение упругих свойств данного компонента. Информация о повреждениях элементарных объемов используется при определении упругих свойств компонентов композита уже на следующем масштабном уровне - уровне локальных свойств.
Объектом моделирования на данном уровне являются объемы композита, обладающие свойством локальной представительности, каждый из которых является совокупностью объемов «базового» уровня [2]. На этом уровне материал рассматривается как упругий, структурно-неоднородный, повреждаемый, характеризующийся наличием явных межфазных границ раздела. Учитывая, что локальные свойства зависят от конкретной конфигурации структуры элементов армирования в пределах объема данного масштабного уровня, для получения надежной информации о локальных свойствах композита в целом необходимо рассматривать статистически представительные выборки свойств таких объемов. В рамках развиваемого подхода к оценке прочностных свойств полагается, что процессы накопления повреждений проявляются в снижении модуля упругости компонентов в пределах данного объема. В качестве количественной меры локальной поврежденности каждого компонента материала используется удельная величина поврежденного объема данного компонента в пределах локального объема (параметр повреждаемости). При достижении параметром повреждаемости любого из компонентов заданной предельной величины полагается, что весь локальный объем композита переходит в разрушенное состояние. Данные о разрушении локальных объемов, полученные в процессе моделирования, используются при оценке состояния композита на следующем масштабном уровне — уровне макроскопических свойств.
В качестве объекта моделирования на макроскопическом уровне используется представительный объем хаотически армированного композита. Данный представительный объем рассматривается как квазиоднородная среда, свойства которой является случайными функциями координат. Характеристики каждой точки такой среды определяются по результатам моделирования соответствующего объема «среднего» уровня, расположение которого в пределах представительного объема определяется координатами выбранной точки. При оценке прочности представительного объема композита полагается, что каждая точка среды может находиться в одном из двух состояний: «разрушенное» или «не разрушенное». Вид состояния определяется по результатам моделирования соответствующего данной точке объема «среднего» уровня. Момент перехода всей среды (представительного объема) в разрушенное состояние находится из решения задачи о появлении соединяющего кластера точек среды в «разрушенном» состоянии (задача о перколяции) [3].
В рамках принятого в работе представления о масштабных уровнях композита ключевым является уровень локальных свойств, поскольку именно этот уровень обеспечивает взаимосвязь между процессами, протекающими на нижнем и верхнем уровнях материала. Для моделирования влияния процесса накопления повреждений в элементарных объемах на локальные механические свойства композита предлагается следующая расчетная методика, ориентированная на использование метода конечных элементов и подобных ему вычислительных методов.
Моделируемый локальный объем представляется в виде совокупности микрообъемов. При использовании метода конечных элементов такое представление может быть получено в процессе построения конечно-элементной сетки, при этом каждый микрообъем отождествляется с отдельным конечным элементом.
Математическая модель композита для масштабного уровня локальных свойств строится в предположении справедливости теории малых деформаций. Состояние моделируемого объема при этом описывается системой уравнений, включающей в себя уравнения равновесия ![]() , уравнения Коши
, уравнения Коши 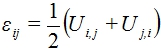 , уравнения состояния
, уравнения состояния ![]() , где
, где ![]() — компоненты тензора деформаций, Ui ,Uj —компоненты вектора перемещений, индекс k обозначает номер компонента композита, П — параметр повреждаемости компонента композита. Для вычисления параметра повреждаемости используется соотношение
— компоненты тензора деформаций, Ui ,Uj —компоненты вектора перемещений, индекс k обозначает номер компонента композита, П — параметр повреждаемости компонента композита. Для вычисления параметра повреждаемости используется соотношение 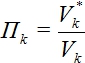 (1), где Vk — объем k-го компонента материала в составе объема, Vk* — «разрушенный» объем k-го компонента. Для оценки состояния каждого из микрообъемов в составе моделируемого объема используется критерий прочности Цая-Ву
(1), где Vk — объем k-го компонента материала в составе объема, Vk* — «разрушенный» объем k-го компонента. Для оценки состояния каждого из микрообъемов в составе моделируемого объема используется критерий прочности Цая-Ву ![]() , где
, где![]() — компоненты тензора напряжений, коэффициенты
— компоненты тензора напряжений, коэффициенты ![]() и
и ![]() вычисляются по значениям пределов прочности компонентов материала при одноосном растяжении и сжатии, а также их сдвиговой прочности. Параметр повреждаемости (1) позволяет для каждого из компонентов рассчитать текущее значение модуля упругости компонента Ek с учетом повреждений, накопленных компонентом
вычисляются по значениям пределов прочности компонентов материала при одноосном растяжении и сжатии, а также их сдвиговой прочности. Параметр повреждаемости (1) позволяет для каждого из компонентов рассчитать текущее значение модуля упругости компонента Ek с учетом повреждений, накопленных компонентом ![]() , где Ek0 — модуль упругости k-го компонента в отсутствие повреждений.
, где Ek0 — модуль упругости k-го компонента в отсутствие повреждений.
Полагается, что для оценки прочности каждого объема уровня локальных свойств применима модель «слабейшего звена», в соответствии с которой объем сохраняет свою несущую способность до тех пор, пока для каждого из его компонентов выполняется условие Пk < Пkmax (3), где Пkmax предельно допустимый удельный объем повреждений в k-м компоненте композита. Нарушение условия (3) рассматривается как признак разрушения объема, и вместе с тем - как признак локального разрушения композита на макроуровне. Вычисленные поля напряжений и деформаций в пределах объема используются для определения локальных свойств композита, в частности локального значения модуля упругости [4]. Данный подход иллюстрируется на примере расчета напряженно-деформированного состояния модельного объема, конечно-элементная модель которого представлена на рис.1.
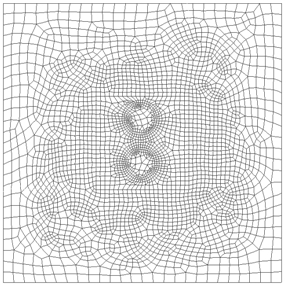
Рис. 1 - Конечно-элементное представление модельного объема композита
На рис. 2 показано развитие кластеров повреждений в процессе возрастания продольной деформации объема. Видно, что зарождение кластеров происходит вблизи боковых границ включений. По мере роста деформации происходит рост кластеров поврежденных объемов, что, в конечном счете, приводит к образованию соединительного кластера, показанного на рис. 2, в.
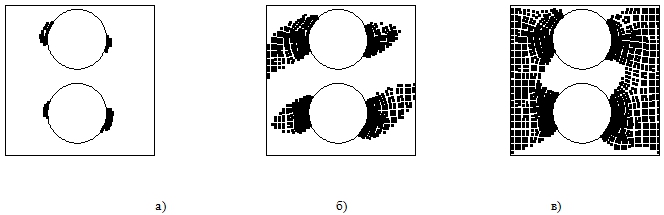
Рис.2 - Развитие кластеров повреждений в модельном объеме композита
Накопление повреждений в объеме сопровождается падением его модуля упругости. На рис. 3 показана зависимость относительного локального модуля упругости El* (El*= , где El - локальный модуль упругости, Ei - модуль упругости более жесткого компонента композита) от продольной деформации объема. По мере возрастания количества поврежденных элементарных объемов, наблюдается снижение локального модуля упругости. Как показывает анализ полученных результатов, к моменту образования соединительного кластера локальный модуль упругости снижается примерно на 25% по отношению к начальному значению.
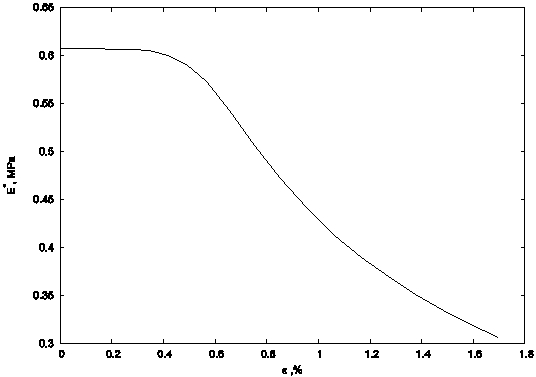
Рис. 3 - Зависимость локального относительного модуля упругости от продольной деформации модельного объема
Таким образом, предложенная расчетная методика позволяет учесть влияние процесса накопления повреждений либо иных процессов, протекающих на низших масштабных уровнях композита, на формирование его эффективных механических свойств.
Литература
- Победря Б.Е. Принципы вычислительной механики композитов // Механика композиционных материалов. – 1996. – №6. – C. 729-746.
- Сидоренко Ю.Н. Прогнозирование механических свойств стохастических композиционных материалов: дис. канд. физ.-мат. наук. - Томск, ТГУ, 2004. – С.142.
- Тарасевич Ю.Ю. Перколяция: теория, приложения, алгоритмы. – М.: Едиториал УРРС, 202. – С.112.
- Лейцин В.Н., Сидоренко Ю.Н. Оценка механических свойств многокомпонентных материалов стохастической структуры // Письма в ЖТФ. – 1999. – Том 25, вып. 12. – С. 89-94.
