АЛГЕБРА ЛОГИКИ В ТЕОРИИ СОБЫТИЙ
АЛГЕБРА ЛОГИКИ В ТЕОРИИ СОБЫТИЙ
Научная статья
Сдвижков О.А. *
Российский государственный университет туризма и сервиса, Пушкино МО, Россия
* Корреспондирующий автор (oasdv[at]yandex.ru)
АннотацияВведено понятие бинарного (булева) события. Рассматриваются события E, задаваемые булевыми функциями E=F (E 1, E 2, …, E n), в которых E 1, E 2, …, E n – булевы события. Доказана теорема о вероятности события заданного такой формулой, на задачах показано применение теоремы. Приведена теорема о структуре таблицы истинности булевой функции E=F (E 1, E 2, …, E n), в которой E 1, E 2, …, E n – булевы события, образующие полную группу событий. Для рассматриваемых событий получен вид формулы полной вероятности, а также получены расчетные формулы для условных вероятностей и формулы Байеса. Приведены задачи на применение полученных формул.
Ключевые слова: вероятность, сумма событий, произведение событий, полная группа событий, булева функция, таблица истинности.
ALGEBRA OF LOGIC IN THEORY OF EVENTS
Research article
Sdvizhkov O.A. *
Russian State University of Tourism and Services, Pushkino, Moscow Oblast, Russia
* Corresponding author (oasdv[at]yandex.ru)
AbstractThe article introduces the concept of the binary (Boolean) event. We consider event E defined by Boolean functions E=F(E1, E2,…,En), in which E1, E2,…,En are Boolean events. A theorem on the probability of an event provided by such a formula is proved, and the application of the theorem is shown on the problems. A theorem on the structure of the truth table of the Boolean function E=F(E 1, E 2,…,En) is given, in which E 1, E 2,…,En are Boolean events that form exhaustive events. For the events under consideration, the form of the formula for the full probability is obtained, as well as the calculated formulas for the conditional probabilities and the Bayes’ formula. The problems on the application of the obtained formulas are given.
Keywords: probability, sum of events, product of events, exhaustive events, Boolean function, truth table.
ВведениеТеория вероятностей [1], [3], [5], в которую входит теория событий, имеет большое прикладное значение [2]. Поэтому рассмотрение вопросов, связанных с теорией событий, несомненно, является актуальным.
Теория событий строится на основе теории множеств [3], задачи на применение алгебры логики в теории множеств рассматриваются в [9, С. 83]. В частности, операциям ∩ и ∪ теории множеств соответствуют операции ∧ и ∨ алгебры логики. Однако алгебра логики в теории событий применяется впервые.
Булевы функции событий
Назовем событие Е бинарным (булевым), если оно является результатом испытания, множество элементарных исходов которого состоит из двух событий Е и . Например, попадание стрелка в мишень – бинарное событие, а выпадение на верхней грани игрального кубика 6 очков – им не является.
Будем рассматривать события, задаваемые булевыми функциями E=F (E 1, E 2, …,
En), в которых E 1, E 2, … E n – булевы события. Например, событие, состоящее в том, что один из двух стрелков попадет в мишень задается булевой функцией:
![]()
![]()
где Е1 – первый стрелок попадет в мишень, Е2 – второй стрелок попадет в мишень.
Также будем предполагать, что события E 1, E 2, …, E n – независимы, в смысле, независимости в совокупности [3, С. 38].
Теорема 1
Пусть событие Е задано булевой функцией E=F (E 1, E 2, …, E n), в которой E 1, E 2, …, E n – независимые булевы события, вероятности которых Р(Е1), Р(Е2), …, Р(Еn). Тогда справедлива формула:
![]() (1)
(1)
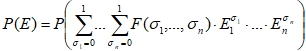 Для любых двух различных булевых наборов (σ1, σ2, …, σn) и (ϑ1, ϑ 2, …, ϑ n) обязательно найдется элемент
Для любых двух различных булевых наборов (σ1, σ2, …, σn) и (ϑ1, ϑ 2, …, ϑ n) обязательно найдется элемент 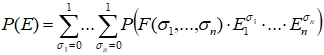 Остается воспользоваться теоремой о вероятности произведении событий и учесть независимость событий Е1, Е2, …, Еn.
Остается воспользоваться теоремой о вероятности произведении событий и учесть независимость событий Е1, Е2, …, Еn.
Задача 1
Событие Е задано функцией ![]() . Найти Р(Е), если Р(Е1) = 0,6, Р(Е2) = 0,9, Р(Е3) = 0,7, применяя:
. Найти Р(Е), если Р(Е1) = 0,6, Р(Е2) = 0,9, Р(Е3) = 0,7, применяя:
А) Таблицу истинности;
В) Преобразования заданной функции.
Решение
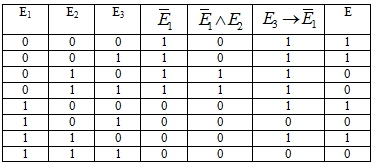
А) Составляется таблица истинности, в которой событие Ei, i=1, 2, 3, имеет значение 1, если оно наступило, и значение 0, в противном случае:![]()
Таблица 1 – Расчеты к задаче 1
Задача 2
Решить задачу 1, если событие Е задано булевой функцией, значения которой (01010111).
Решение
А) Составляется таблица истинности:
Таблица 2 – Входные данные
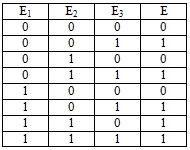
Таблица 3 – Карта Карно к задаче 2
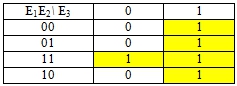
Задача 3
Решить задачу 1, если событие Е задано булевой функцией, значения которой (0001000100010001), р(Е1)=0,6; р(Е2)=0,7; р(Е3)=0,8; р(Е4)=0,9.
Решение
А) Составляется таблица истинности:
Таблица 4 – Входные данные к задаче 3
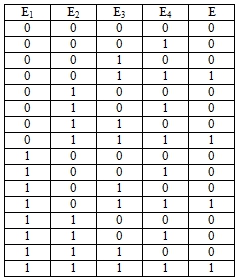
Таблица 5 – Карта Карно к задаче 3
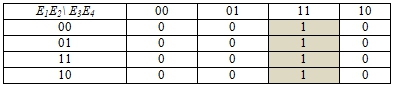
Из блока единичных значений следует Е= Е3Е4, а значит ![]() .
.
Пусть событие Е задано булевой функцией E=F (E 1, E 2, …, E n), в которой E 1, E 2, …, E n, – независимые булевы события, вероятности которых Р(Е1), Р(Е2), …, Р(Еn), и есть такой набор (σ1, σ2, …, σn), для которого F (σ1, σ2, …, σn) = 0, а для всех остальных наборов F=1. Тогда вычислить Р(Е) можно по формуле:
![]()
Например, ![]() , Р(Е1)=0,7, Р(Е2)=0,6, Р(Е3)=0,8. Тогда таблица истинности имеет вид:
, Р(Е1)=0,7, Р(Е2)=0,6, Р(Е3)=0,8. Тогда таблица истинности имеет вид:
Таблица 6 – Расчетная таблица
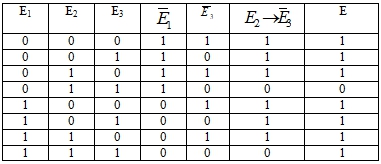
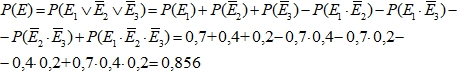 Булева функция события, зависящего от полной группы событий
Булева функция события, зависящего от полной группы событий
Теорема 2
В булевой функции E=F (E 1, E 2, …, E n) события E 1, E 2, …, E n образуют полную группу событий тогда и только тогда, когда F (E 1, E 2, …, E n) =1, если среди значений E 1, E 2, …, E n есть только одна единица.
Доказательство
Если события E 1, E 2, …, E n образуют полную группу событий, то они попарно несовместны и их объединение является достоверным событием. Поэтому одновременно два и более из событий E 1, E 2, …, E n наступить не могут, что и отражает условие F (E 1, E 2, …, E n) =1, если среди значений E 1, E 2, …, E n есть только одна единица.
Теорема 3
Пусть событие Е задано булевой функцией E=F (E 1, E 2, …, E n), в которой события E 1, E 2, …, E n образуют полную группу событий и имеют вероятности p1, p2, …, pn, ![]() . Тогда формула полной вероятности события Е записывается в виде:
. Тогда формула полной вероятности события Е записывается в виде:
Если событие Е задано булевой функцией E=F (E 1, E 2, …, E n), в которой события E 1, E 2, …, E n образуют полную группу событий, то условные вероятности Р(Е| Еi) находятся по формулам:
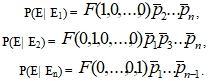 (3)
(3)
Следствие 2
Если событие Е задано булевой функцией E=F (E 1, E 2, …, E n), в которой события E 1, E 2, …, E n образуют полную группу событий, то в формуле Байеса
Р(Еi| Е) = Р(Еi) Р(Е| Еi) /P(Е) вероятности Р(Е| Еi) находятся по формулам (3), а вероятность P(Е) – по формуле (2).
Задача 4
Событие Е задано булевой функцией:
![]()
Проверить, что события Е1, Е2 образуют полную группу событий.
Решение
Составляется таблица истинности:
Таблица 7 – Расчеты к задаче 4
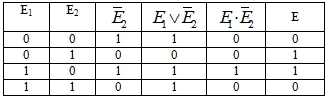
По теореме 2 из таблицы 7 следует, что Е1, Е2 образуют полную группу событий.
Задача 5
Событие Е задано формулой:
Таблица 8 – Расчеты к задаче 5
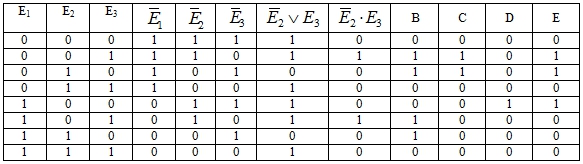
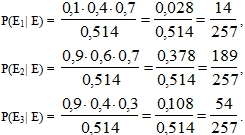
Заключение
Введенные понятия и полученные результаты показывают, что применение алгебры логики в теории событий открывает новые возможности по решению многих задач теории событий.
| Конфликт интересов Не указан | Conflict of Interest None declared |
Список литературы / References
- Венцель Е.С. Теория вероятностей. / Е.С. Венцель – М.: Наука, 1964, – 564 с.
- Венцель Е.С. Прикладные задачи теории вероятностей. / Е.С. Венцель, Л.А. Овчаров – М.: Радио связь, 1983. – 416 с.
- Вуколов Э.А. Сборник задач по математике для втузов. Часть 4 / Вуколов Э.А., Ефимов А.В., Земсков В.Н., Поспелов А.С. Под общ. ред. А.В. Ефимова и А.С. Поспелова. – 3-е изд. перераб. и доп. – М.: Издательство Физико-математической литературы, 2004. – 432 с.
- Гаврилов Г.П. Задачи и упражнения по дискретной математике: Учебное пособие – 3-е изд., перераб. / Г.П. Гаврилов, А.А. Сапоженко – М.: ФИЗМАТЛИТ, 2003. – 416 с.
- Гнеденко Б.В. Курс теории вероятностей. /Б.В. Гнеденко – М.: Физматгиз, 1961, – 406 с.
- Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения. 3-е издание. / Я.М. Ерусалимский – М.: Вузовская книга, 2000. – 280 с.
- Сдвижков О.А. Дискретная математика и математические методы экономики с применением VBA Excel. / О.А. Сдвижков – М.: ДМК Пресс, 2012. – 212 с.
- Супрун В.П. Основы теории булевых функций. / В.П. Супрун – М.: ЛЕНАНД, 2017. – 208 с.
- Тишин В.В. Дискретная математика в примерах и задачах. / В.В. Тишин – СПб. БХВ-Петербург, 2008. – 352 с.
- Яблонский С.В. Введение в дискретную математику: Учебное пособие для вузов / Под ред. В.А. Садовничего. – 4-е изд., стер. – М.: Высш. шк.; 2003. – 384 с.
Список литературы на английском языке / References in English
- Wenzel E.S. Teoriya veroyatnostei [Probability Theory] / E.S. Wenzel – M.: Nauka, 1964, – 564 p. [in Russian]
- Wenzel E.S. Prikladnye zadachi teorii veroyatnostei [Applied Problems of Probability Theory] / E.S. Wenzel, L.A. Ovcharov – M.: Radio Communication, 1983. – 416 p. [in Russian]
- Vukolov Ye.A. Sbornik zadach po matematike dlya vtuzov [Collection of Math Problems for Technical Colleges]. / Vukolov Ye.A., Efimov A.V., Zemskov V.N., Pospelov A.S. // Part 4 / Under the general. ed. of A.V. Efimov and A.S. Pospelov. – 3rd revised. – M.: Publishing House of Physics and Mathematics, 2004. – 432 p. [in Russian]
- Gavrilov G.P. Zadachi i uprazhneniya po diskretnoi matematike: Uchebnoe posobie – 3-e izd., pererab. [Tasks and Exercises in Discrete Mathematics: Textbook – 3rd, revised] / G.P. Gavrilov, A.A. Sapozhenko – M.: FIZMATLIT, 2003. – 416 p. [in Russian]
- Gnedenko B.V. Kurs teorii veroyatnosti [Probability Theory Course] / B.V. Gnedenko – M.: Fizmatgiz, 1961, – 406 p. [in Russian]
- Yerusalimskij Ya.M. Diskretnaya matematika: teoriya, zadachi, prilozheniya. 3-e izdanie. [Discrete Mathematics: Theory, Problems, Applications. 3rd edition] / Ya.M. Yerusalimsky – M.: University Book, 2000. – 280 p. [in Russian]
- Sdvizhkov O.A. Diskretnaya matematika i matematicheskie metody ekonomiki s primeneniem VBAExcel [Discrete Mathematics and Mathematical Methods of Economics using VBAExcel] / O.A. Sdvizhkov – M.: DMK Press, 2012. – 212 p. [in Russian]
- Suprun V.P. Osnovy teorii bulevykh funktsii [Fundamentals of the Theory of Boolean Functions]. / V.P. Suprun – M.: LENAND, 2017. – 208 p. [in Russian]
- Tishin V.V. Diskretnaya matematika v primerakh i zadachakh. [Discrete Mathematics in Examples and Problems] / V.V. Silence – St. Petersburg. BHV-Petersburg, 2008. – 352 p. [in Russian]
- Yablonskii S.V. Vvedenie v diskretnuyu matematiku: Uchebnoe posobie dlya vuzov [Introduction to Discrete Mathematics: Textbook for High Schools] / Ed. by V.A. Sadovnicii. – 4th ed., revised. – M.: Vysshaya Shkola; 2003. – 384 p. [in Russian]
