АКУСТИЧЕСКОЕ ИЗЛУЧЕНИЕ В УПРУГОЙ СРЕДЕ ОТ ВНУТРЕННЕГО ДЕФЕКТА С ИЗЛОМОМ
Беркович В.Н.
ORCID: 0000-0003-0915-7170, Доктор физико-математических наук,
Донской казачий государственный институт пищевых технологий и бизнеса (филиал) «МГУТУ им. К.Г. Разумовского (ПКУ) » в г. Ростове-на-Дону
АКУСТИЧЕСКОЕ ИЗЛУЧЕНИЕ В УПРУГОЙ СРЕДЕ ОТ ВНУТРЕННЕГО ДЕФЕКТА С ИЗЛОМОМ
Аннотация
Рассмотрена математическая модель описания волнового процесса, порождаемого дефектом материала в некоторой неограниченной области, находящейся в состоянии пространственного сдвига. Физический процесс возникновения колебаний изучается на стадии образования дефекта с изломом, появившимся при развитии внутреннего дефекта под воздействием нагрузок и формирующего дефект с изломом. Излучающим предполагается лишь новый дефект, появившийся в результате этого процесса. Проблема состоит в отыскании характеристик возникающей при этом акустической эмиссии (АЭ). Математическая постановка сформулированной проблемы приводит к смешанной краевой задаче математической физики. Последняя, в свою очередь, сводится к эквивалентной системе граничных интегральных уравнений (ГИУ). Установлена разрешимость ГИУ и структура их решений.
Предлагаемая к рассмотрению проблема связана с физико-математическим описанием волновых полей, порождаемых АЭ от дефектов в материалах.
Ключевые слова: неразрушающий контроль, акустическая эмиссия, дефект с изломом, граничное интегральное уравнение.
Berkovich V.N.
ORCID: 0000-0003-0915-7170, PhD in Physics and Mathematics,
Don Cossack State Institute of Food Technology and Business branch of FSBEI of HE «K.G. Razumovsky Moscow State University of technologies and management (the First Cossack University)» in Rostov-on-Don
ACOUSTIC RADIATION IN FLEXIBLE ENVIRONMENT FROM INTERNAL DEFECT WITH FRACTURE
Abstract
A mathematical model describing the wave process generated by a material defect in an unlimited region in the state of spatial displacement is considered. The physical process of the appearance of oscillations is studied at the stage of formation of a defect with a fracture that appeared when an internal defect developed under the influence of loads and formed a defect with a break. Only the new defect that appears as a result of this process is assumed to be radiating. The problem consists in finding the characteristics of acoustic emission (AE) arising in this process. The mathematical formulation of the formulated problem leads to a mixed boundary-value problem of mathematical physics. The latter, in turn, reduces to an equivalent system of boundary integral equations (BIE). The solvability of BIE and the structure of their solutions are established.
The problem proposed for consideration is related to the physical and mathematical description of the wave fields generated by AEs from defects in materials.
Keywords: non-destructive control, acoustic emission, defect with a fracture, boundary integral equation.
Задачи оценки и прогнозирования остаточного ресурса объектов технологического оборудования предприятий задачи приобретают особую актуальность, когда замена старого оборудования более современным требует серьезных материальных затрат, которые для целей производства в ряде случаев могут оказаться неоправданными.
Существующие способы анализа состояний предразрушения в процессе эксплуатации основаны на использовании различных методов неразрушающего контроля, например [1] и др. Одним из эффективных методов оценки стадий предразрушения конструкционных материалов является метод АЭ, детально исследованный и развитый в [2], [3]. Метод обладает уникальными возможностями, так как позволяет выявлять именно растущие, наиболее опасные дефекты. Для оценки параметров этих дефектов необходимо математическое моделирование волновых полей, зависящих от характера, формы и расположения дефектов в материале.
В работе [4] была построена математическая модель волнового поля при АЭ от двух независимо образовавшихся дефектов, выходящих на свободную поверхность тела. В предлагаемом исследовании моделируется фрагмент накопления повреждений, когда внутренний дефект, уже имеющийся в материале, порождает следующий, излучающий сигналы АЭ. В частности, этап ветвления трещины описан в [5]. Моделирование ситуации, изложенной выше, приводит к рассмотрению задачи динамической теории упругости об антиплоских колебаниях массивного тела, содержащего внутренний дефект J в форме ломаной ![]() , состоящей из двух звеньев
, состоящей из двух звеньев ![]() длины
длины ![]() и составляющих с направлением свободной границы Г тела углы
и составляющих с направлением свободной границы Г тела углы ![]() соответственно
соответственно ![]() . При этом массивное тело моделируется упругим полупространством Ω, граница Г которого предполагается свободной от нагрузок, а дефект J – разрезом в форме ломаной
. При этом массивное тело моделируется упругим полупространством Ω, граница Г которого предполагается свободной от нагрузок, а дефект J – разрезом в форме ломаной ![]() с изломом в точке A1. Ближайшая к свободной границе Г точка A0 удалена от нее на расстояние h. Расположение дефекта
с изломом в точке A1. Ближайшая к свободной границе Г точка A0 удалена от нее на расстояние h. Расположение дефекта ![]() в полупространстве показано на Рис.1. Ненулевые когерентные источники гармонических колебаний смещений сдвига равной интенсивности задаются лишь на берегах
в полупространстве показано на Рис.1. Ненулевые когерентные источники гармонических колебаний смещений сдвига равной интенсивности задаются лишь на берегах ![]() разреза, ближайшего к границе в виде
разреза, ближайшего к границе в виде ![]() , на берегах
, на берегах ![]() смещения предполагаются равными нулю, волны смещений убегают на бесконечность, где их амплитуды затухают. При указанных условиях требуется восстановить волновое поле смещений во всей области Ω.
смещения предполагаются равными нулю, волны смещений убегают на бесконечность, где их амплитуды затухают. При указанных условиях требуется восстановить волновое поле смещений во всей области Ω.
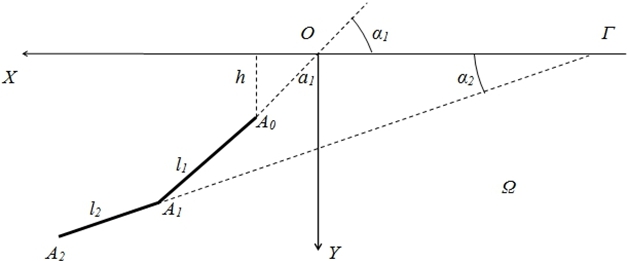
Рис.1 – Внутренний дефект J с изломом в упругом полупространстве Ω
Для решения проблемы рассматривается краевая смешанная задача для дифференциальных уравнений динамической теории упругости [5], [6] в упругом полупространстве Ω со свободной границей Г и разрезами J1,2 конечной длины, формирующими ломаную J. Представление результирующего колебания смещений в виде:
![]() (1)
(1)
позволяет свести поставленную проблему к следующей задаче математической физики для амплитуд смещений ![]() полупространства Ω:
полупространства Ω:
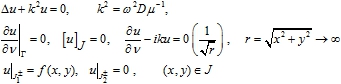 (2)
(2)
где D – плотность материала, μ – модуль сдвига, v – внешняя нормаль к границе, ![]() – скачок функции на ломаном разрезе J. Во второй строке (2) указаны условия распространения волн на бесконечность, где их амплитуды исчезают Во второй строке (2) указаны условия распространения волн на бесконечность, где их амплитуды исчезают (условия излучения) [6]. Решения краевой задачи рассматривается в общем случае, как элементы пространства Соболева
– скачок функции на ломаном разрезе J. Во второй строке (2) указаны условия распространения волн на бесконечность, где их амплитуды исчезают Во второй строке (2) указаны условия распространения волн на бесконечность, где их амплитуды исчезают (условия излучения) [6]. Решения краевой задачи рассматривается в общем случае, как элементы пространства Соболева ![]() [7].
[7].
Метод исследования краевой задачи (2) основан на её сведении с помощью построения функций Грина ![]() для уравнения Гельмгольца (2). При этом функции Грина удовлетворяют первому граничному условию (2). Тогда имеет место представление комплексных амплитуд смещений полупространства в форме криволинейных интегралов по правым берегам разрезов
для уравнения Гельмгольца (2). При этом функции Грина удовлетворяют первому граничному условию (2). Тогда имеет место представление комплексных амплитуд смещений полупространства в форме криволинейных интегралов по правым берегам разрезов ![]() :
:
![]() (3)
(3)
В формуле (3) ![]() – безразмерные скачки напряжений на
– безразмерные скачки напряжений на ![]() соответственно. Искомое поле смещений может быть восстановлено после определения скачков
соответственно. Искомое поле смещений может быть восстановлено после определения скачков ![]() .
.
Помещая точку наблюдения на берега разрезов и переходя к локальным координатам вдоль берегов, приходим к следующей системе ГИУ относительно ![]() :
:
![]() (4)
(4)
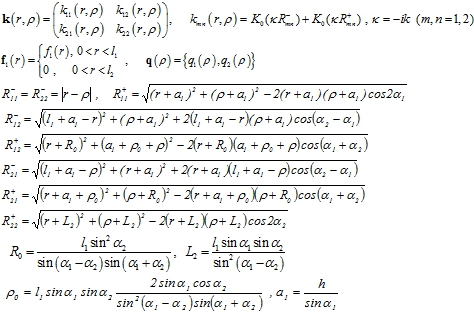
В выражениях (4) учтено, что ![]() вне разрезов,
вне разрезов, ![]() функция Макдональда [8], h – расстояние от точки A0 до свободной границы Г,
функция Макдональда [8], h – расстояние от точки A0 до свободной границы Г, ![]() -расстояние от точки A0 до точки пересечения направления звена дефекта J1 со свободной границей Г, величины
-расстояние от точки A0 до точки пересечения направления звена дефекта J1 со свободной границей Г, величины ![]() связаны с расстояниями от точки излома A1 до свободной границы вдоль направлений звеньев J. Для удобства записи и описания дальнейших результатов введем вектор-функцию
связаны с расстояниями от точки излома A1 до свободной границы вдоль направлений звеньев J. Для удобства записи и описания дальнейших результатов введем вектор-функцию ![]() как продолжение вектор-функции
как продолжение вектор-функции ![]() на весь отрезок
на весь отрезок ![]() . Тогда систему (4) можно преобразовать к виду, аналогично рассмотренному в работе [4]:
. Тогда систему (4) можно преобразовать к виду, аналогично рассмотренному в работе [4]:
![]() (5)
(5)
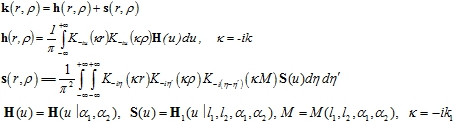
При этом оказывается, что оператор левой части K представим в виде суммы однозначно обратимого оператора H и компактного оператора S, действующих в пространствах ![]() дробной гладкости.
дробной гладкости.
Структура решения (5). детально исследована в [4] и имеет единственное представление:
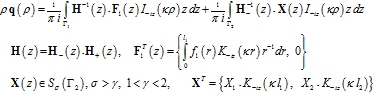 (6)
(6)
При этом контур Г2 лежит выше ![]() -пространство вектор - функций
-пространство вектор - функций ![]() , сходящихся к 0 с весом zσ в некоторой полосе, содержащей
, сходящихся к 0 с весом zσ в некоторой полосе, содержащей ![]() -результат факторизации H(z) относительно
-результат факторизации H(z) относительно ![]() .
.
Доказательство теоремы основано на результатах [9]. Последующая подстановка решения (6) в уравнение (5) приводит к отысканию неизвестных векторов ![]() из некоторой вспомогательной системы интегральных уравнений второго рода с компактным оператором в пространстве функций
из некоторой вспомогательной системы интегральных уравнений второго рода с компактным оператором в пространстве функций ![]() .
.
Компактность оператора системы позволяет представить его в виде суммы конечномерного и достаточно малого в соответствующей норме, что позволяет воспользоваться численными методами для решения системы уравнений с компактным оператором, а, следовательно, и для решения исходной краевой задачи.
Восстановление волнового поля в исследуемой области с дефектом основано на представлении (3) и решении (6) уравнений (5). Для восстановления волнового поля свободной поверхности необходимо. в формулах (3) устремить точку наблюдения (x,y) на границу Г полупространства.
Предлагаемый подход может быть применен при рассмотрении обратных задачи восстановления на основе анализа сигналов АЭ неизвестных физических параметров процесса развития внутренних дефектов внутри массивного упругого тела. Детальный анализ рассмотренной модели позволяет связать теоретические результаты с экспериментальными данными по обработки и анализу регистрируемых на свободной поверхности сигналов АЭ [10]. На основе построения необходимых амплитудно-частотных характеристик смещений точек свободной поверхности для восстановления требуемых параметров можно воспользоваться методами, разработанными в [11], [12] и др., для решения обратных задач динамической теории упругости.
Список литературы / References
- Ермолов И.Н. Акустические методы контроля. Сер. « Неразрушающий контроль» / Ермолов И.Н., Алешин Н.П., Потапов А.И. // М. Высшая школа. Книга 2. – – 287 с.
- Буйло С.И. Физико-механические, статистические и химические аспекты акустико-эмиссионной диагностики. – Ростов- на-Дону. Изд-во Южного федерального университета. – – 144 с.
- Builo S.I. Physical, Mechanical and Statistical Aspects of Acoustic Emission Diagnostics. In: Physics and Mechanics of New Materials and Their Applications. New York: Nova Science Publishers. Chapter – 2013. –444 p.
- Беркович В.Н. Колебания упругого полупространства с двумя излучающими дефектами конечной длины / Беркович В.Н., Бабкин А.В. // Международный научно-исследовательский журнал. –2017. – № 4. –С. 101-104. DOI: https://doi.org/10.23670/IRJ.2017.58.042
- Рекач В.Г. Руководство к решению задач по теории упругости. – М. Высшая школа, 1977. – 275 с.
- Исраилов М.Ш. Динамическая теория упругости и дифракция волн. – М. Изд. МГУ. – 1988. – 204 с.
- Бесов О.В. Интегральные представления функций и теоремы вложения / Бесов О.В., Ильин В.П., Никольский С.М.// – М. Наука. 1975. – 478 с.
- Лебедев Н.Н. Специальные функции и их приложения. – М.–Л.Наука. 1968. – 358 с.
- Беркович В.Н. О точном решении одного класса интегральных уравнений смешанных задач упругости и математической физики.// Докл. АН СССР. –1982. –Т.267. –№2. – С.327– 330.
- Буйло С.И. Диагностика предразрушающего состояния материалов по параметрам амплитудного распределения сигналов сопутствующего акустического излучения. – Дефектоскопия, 2012, № 11, С. 32-45.
- Романов В.Г. Обратные задачи математической физики. – М. Наука. 1984. – 262с.
- Ватульян А. О. Обратные задачи в механике деформируемого твердого тела. – М. Физматлит, – – 223 с.
Список литературы на английском языке / References in English
- Ermolov I.N. Acusticheskiye metodi kontrolya. Ser. “Nerasrushayuschiy control”[Acoustical Testing Methods. Ser. “Non-destructive testing”] / I.N.Ermolov, N.P.Aleshin, A.I. Potapov // – M. Visshaya shkola. Book 2. – 1991. – 287 P. [in Russian]
- Builo S.I. Fiziko-mehanicheskiye, statisticheskiye I himicheskiye aspekti akustiko-emissionnoi diagnostiki [Physical, Mechanical and Statistical and Chemical Aspects of Acoustic Emission Diagnostics] / S.I.Builo – Rostov-na-Donu. Izdatelstvo – 2016. – 144 P. [in Russian]
- Builo S.I. Physical, Mechanical and Statistical Aspects of Acoustic Emission Diagnostics. In: Physics and Mechanics of New Materials and Their Applications. New York: Nova Science Publishers. Chapter 15. – 2013. –444 P.
- Berkovich V.N. Kolebaniya uprugogo poluprostranstva c dvumya izluchayuschimi defektami konechnoi dlini [Vibration of Elastic Half-Space Containing Two Radiating Defects of Finite Length] / Berkovich V.N., Babkin A.V. // Mezhdunarodniy nauchno-issledovfntlskiy zhurnal [International Research Journal] – –№ 4. – P. 101-104. DOI: https://doi.org/10.23670/IRJ.2017.58.042 [in Russian]
- Rekach V.G. Rukovodstvo k resheniyu zadch po teorii uprugosti [The Guide to Solve Elasticity Problems] / V.G. Rekach – М.: Visshaya shkola. –1977. –275 P. [in Russian]
- Israilov M.Sh. Dinamicheskaya teoriya uprugosti i difraktsiya voln [Dynamic Theory of Elasticity and Wave Diffraction] / M.Sh. Israilov.– М. Izdatrlstvo MGU. –1992. –204 P. [in Russian]
- Lebedev N.N. Spetzialniye funktzii i ih prilogeuiya.[Special Functions and Its Applications] / N.N.Lebedev– М.-L.: Nauka.–1968. – 358 P. [in Russian]
- Besov O.V. Integralniye predstavleniya funktziy i teoremi [Integral Representation of Functions and Embedding Theorems] / O.V.Besov, V.P.Ilyin, S.M.Nikolskiy–М. Nauka. – 1975. – 478 P. [in Russian]
- Berkovich V.N. O tochnom reshenii odnogo klassa integralnih uravneniy smeshannih zadach uprugosti i matematicheskoy fiziki. [On the Exact Solution of Some Class of Integral Equations for Mixed Problems of Elasticity and Mathematical Physics] // Dokladi Akademii Nauk SSSR.–1982. –V.267. –№2. – P. 327– 330. [in Russian]
- Builo S.I. Diagnostika predrazrushayuschego sostoyaniya materialov po parametram amplitudnogo raspredeleniya signalov soputstvuyuschego akusticheskogo izlucheniya. [Pre-destuctive testing of state of materials based on parameters of amplitude signal distribution of the attendant acoustic emission ] // – Дефектоскопия, [Non-destructive testing]. –2012. –№11. – P. 32–45.[in Russian]
- Romanov V.G. Obratniye zadachi matemsticheskoi fiziki [Inverse Problems in Mathematical Physics] / G. Romanov. –М. Nauka. – 1984. – 262 P. [in Russian]
- Vatulyan A.O. Obratniye zadachi v mehanike deformiruemogo tverdogo tela [Inverse Problems in Solid Mechanics] / A.O.Vatulyan. –М. Fismatlit.– 2007. – 223 P. [in Russian]
