RANDOM NUMBER GENERATOR FOR SIMULATING THE RESULTS OF MONITORING BIRD POPULATIONS IN THE TERRITORY OF WIND POWER PLANTS
RANDOM NUMBER GENERATOR FOR SIMULATING THE RESULTS OF MONITORING BIRD POPULATIONS IN THE TERRITORY OF WIND POWER PLANTS
Abstract
An algorithm for obtaining random numbers that obey an arbitrary integral distribution function has been suggested, and a programme called Generator has been developed to produce sample data in accordance with this function. The programme was tested by comparing samples generated using the proposed method for various distributions with sample data calculated using known standard functions. The results of calculating statistical parameters for normal, exponential, and sinusoidal distributions found using the Generator programme are well in agreement with the calculations obtained using standard functions. The method is quite simple and can be easily implemented in any algorithmic language that provides the ability to connect a function for generating random integers. The findings are recommended for use in modelling the impact of wind farms on birds using the results of monitoring activities in their territory and buffer zones.
1. Введение
1.1. Постановка проблемы
Использование генераторов случайных величин позволяет решать ряд практически важных задач, относящихся к выбору оптимального числа участков наблюдения, оценке доверительных интервалов для измеряемых характеристик, оценке точности прогнозирования тех или иных параметров, зависящих от многих условий, и т.д.
В частности, актуальными являются выбор оптимального количества и размера площадок наблюдения за птицами на территории ветровой электростанции при организации мониторинговых мероприятий с целью исследования влияния турбин на орнитофауну в зоне эксплуатации ВЭС, оценка доверительных интервалов для измеряемых характеристик птиц, оценка точности прогнозирования тех или иных параметров орнитокомплексов.
Всё возрастающее увеличение производственных мощностей в области ветровой энергетики требует существенных материальных затрат на проведение исследований влияния турбин ветровых электростанций (ВЭС) на птиц и рукокрылых. Предварительная орнитологическая экспертиза на территории будущей станции является первым шагом перед принятием решения о возможности её строительства. Мониторинговые мероприятия по изучению влияния конкретного ветрового парка на орнитокомплексы птиц, как правило, продолжаются в течение всего периода его эксплуатации , , , . Специфика статистического анализа результатов мониторинга состоит в том, что, несмотря на огромный массив измеренных характеристик птиц, численность которых иногда достигает десятков тысяч и более особей различного вида, наблюдатель не имеет возможности повторить условия получения данных. В этом случае целесообразно обратиться к методам математического моделирования ситуации. Один из методов численного моделирования связан с генерированием случайных величин в соответствии с теми законами распределения, которые наиболее часто встречаются в задачах орнитологии. К ним относятся, например, нормальный закон, распределение Стьюдента, экспоненциальное распределение, а также нестандартные многофакторные функции распределения.
1.2. Цель выполнения работы и постановка задачи
Цель исследования состоит в разработке генераторов случайных величин, которые подчиняются законам распределения, используемых при статистическом анализе результатов мониторинга орнитокомплексов на территории ВЭС. Для достижения цели необходимо было решить следующие задачи:
- провести анализ генераторов случайных чисел для получения выборочных данных, подчиняющихся законам распределения, которые могут использоваться при моделировании ситуаций, связанных с анализом влияния ВЭС на птиц;
- разработать алгоритм и создать программу для генерирования случайных чисел с произвольным законом распределения.
2. Результаты работы
2.1. Анализ алгоритмов и методов генерирования случайных чисел
Для получения случайных чисел с заданным распределением обачно применяется генератор случайных чисел с равномерным распределением
, . В качестве примера можно сослаться на труды Д. Бокса, М. Мюллера-Д. Марсальи , которые посвящены алгоритмам получения нормально распределённых выборочных данных в соответствии с законом Лапласа. Описание различных методов генерирования нормально распределённых случайных чисел можно найти во многих публикациях , , , .В работе
проведён сравнительный анализ получения случайных величин методом Д. Бокса, методом М. Мюллера-Д. Марсальи и с использованием стандартной функции normal_distribution в среде программирования Visual C++. Сгенерированные числа представлялись в виде интервального вариационного ряда. Проверка гипотезы о выполнении закона нормального распределения выборки проводилась с помощью χ2 — критерия Пирсона для 5%-го уровня значимости при s-3 степенях свободы, где s — число интервалов, по формуле:где ni — количество чисел, сгенерированных в i-м интервале,
n’i — количество чисел в i-м интервале, вычисленное в соответствии с законом нормального распределения по формуле
n — объём выборки,
δ — размер интервала,
xi — координата середины i –го интервала,
f(xi) — дифференциальная функция распределения для нормированного нормального закона с математическим ожиданием, равным нулю, и среднеквадратичным отклонением, равным единице,
На основании проведённых расчётов сделан вывод, что рассмотренные методы обеспечивают получение адекватных выборок. Наименьшее значение χ2-критерия Пирсона показал метод полярных координат Бокса-Мюллера-Марсальи.
Различные способы генерирования нормально распределённых случайных чисел широко применяются на практике. Близкая ситуация наблюдается для многих других часто используемых распределений, описание которых можно найти в литературе. В настоящей работе предлагается алгоритм, который не привязан к конкретной функции распределения. Актуальность создания подобного алгоритма обусловлена наличием круга задач в прикладной математической статистике в случае обращения к нестандартным и многофакторным функциям распределения.
2.2. Алгоритм генерирования случайных чисел для произвольной функции распределения
Пусть требуется создать выборку из непрерывных случайных чисел, подчиняющихся интегральной функции распределения F(x). Алгоритм генерирования псевдослучайных чисел представим в виде следующих этапов.
На первом этапе необходимо определиться с интервалом изменения функции F(x). В теоретических исследованиях он зачастую охватывает множество всех действительных чисел. При решении прикладных задач обычно используют конечные интервалы. Например, в случае нормального закона распределения часто ограничиваются отрезками [M(x)-3σ, M(x)+3σ] или [M(x)-4σ, M(x)+4σ], где M(x) — математическое ожидание, σ — среднее квадратичное отклонение. Все расчёты в дальнейшем будут проводиться для случая генерирования чисел на конечном отрезке [a,b]. В качестве базового источника случайных чисел выбран генератор целых случайных чисел с равномерным распределением на отрезке [0, N].
На втором этапе требуется подготовить вспомогательный массив данных из трёх строк и N+1 столбцов (см. табл. 1). Первая строка содержит целые числа, часть которых используется для формирования выборки из m чисел в соответствии с равномерным распределением.
Во вторую строку помещаются значения чисел xi с шагом δ=(b-a)/N :
a0=a, a1=a+δ, a2=a+2δ, … , aN=b.
Третья строка заполняется значениями интегральной функции распределения F(x) в точках ai=a+iδ, i=0, 1, ... , N.
Таблица 1 - Вспомогательная таблица для генерирования случайных чисел
i | 0 | 1 | 2 | … | N |
ai | a0=a | a1=a+δ | a2=a+2δ | … | aN=a+Nδ |
F(x) | F(a0=a) | F(a1) | F(a2) | … | F(aN=b) |
Величина δ-интервала выбирается таким образом, чтобы разность значений F(x) в соседних столбцах не превышала требуемой точности вычислений ε: F(ai)-F(ai-1)<ε.
Интегральная функция F(x) с изменением аргумента на заданном отрезке от a до b монотонно возрастает от 0 до 1. Поэтому требование к размеру интервала δ не является слишком жёстким. Тестовые испытания показали, что точность расчётов F(x) на уровне ε=10-4 при не слишком больших величинах дифференциальной функции распределения обеспечивается выбором значения N≈104-105. В случае необходимости получения меньшей погрешности следует отказаться от одинакового размера интервала и привязать его к скорости изменения F(x).
На третьем этапе запускается генератор случайных m целых чисел n1, n2, n3,…nm в соответствии с равномерным их распределением на отрезке [0, N]. Вероятность того, что используемый генератор выдаст любое число ks, которое меньше выборочного значения ni, равна
P(ks<ni)=ni/(N+1), i=1, 2, … , m.
Формирование выборки из m вещественных случайных чисел x в соответствии с функцией распределения F(x) проводится следующим образом. В третьей строке таблицы 1 определяется j-й интервал, для которого вероятность P(ks<nj) находится в пределах
F(aj)≤ P(ks<ni)<F(aj+1)).
Найденному неравенству соответствует полуинтервал [aj, aj+1), где с точностью до ε=1/(N+1) находится искомое случайное число, соответствующее функции распределения F(x). Обозначим его значение через xj, тем самым подчёркивая, что оно принадлежит j–му интервалу.
Используя линейную экстраполяцию, получим:
Формула (4) завершает преобразование одного целого числа nj, полученного с помощью целочисленного генератора с равномерным распределением на отрезке [0, N], в вещественное число xj на отрезке [a, b]. Многократное её применение к случайным целым числам n1, n2, n3, … , nm обеспечивает получение искомой выборки из m вещественных чисел x1, x2, x3, …, xm, которая подчиняется заданной интегральной функции распределения F(x).
2.3. Разработка программы Generator и тестирование разработанного метода получения случайных чисел с заданной функцией распределения
Программа Generator реализована в среде алгоритмического языка Phyton. Структурно она состоит из шести блоков.
Блок 1 обеспечивает ввод формулы для расчёта значения интегральной функции распределения, объёма выборки и числа интервалов для получения интервального вариационного ряда. Интерфейс программы написан на Tkinter. На рисунке 1 представлен пример ввода исходной информации для генерирования выборки из 1000 случайных чисел на отрезке [-5, 5] с нормальным распределением при математическом ожидании, равным 0, и среднеквадратичным отклонении, равным 1.

Рисунок 1 - Пример ввода информации для генерирования случайных чисел с нормальным распределением в тестирующем эксперименте
В блоке 3 генерируется m целых чисел n1, n2, n3, …, nm, равномерно распределенных в заданном диапазоне [0, N]. Эти числа используются для подстановки в формулу (4), которая обеспечивает генерирование числа в соответствии с заданной функцией распределения.
Блок 4 обеспечивает формирование выборки из случайных чисел, подчиняющихся интегральной функции распределения F(x), и при необходимости строит интервальный вариационный ряд и гистограмму, определяет среднее выборочное значение, дисперсию, среднеквадратичное отклонение, и критерий Пирсона. В таблице 2 представлен интервальный вариационный ряд в случае генерирования случайных чисел с нормальным распределением с параметрами, приведёнными на рисунке 1.
Таблица 2 - Таблица сравнения наблюдаемых и теоретических частот
Интервал | Наблюдаемые | Теоретические |
[-4,75, -2,61) | 7,00 | 6,04 |
[-2,61, -1,90) | 26,00 | 28,03 |
[-1,90, -1,19) | 87,00 | 93,35 |
[-1,19, -0,47) | 194,00 | 197,76 |
[-0,47, 0,24) | 287,00 | 266,60 |
[0,24, 0,95) | 222,00 | 228,78 |
[0,95, 1,66) | 121,00 | 124,96 |
[1,66, 2,38) | 47,00 | 43,42 |
[2,38, 3,09) | 9,00 | 9,59 |
Примечание: вычисленное значение критерия Пирсона: 3,0; критическое значение критерия Пирсона: 19.7
Графическая интерпретация полученной выборки в виде гистограммы осуществляется в блоке 5 с помощью библиотеки matplotlib. Пример гистограммы, соответствующий интервальному вариационному ряду с параметрами, приведёнными в таблице 2, представлен на рисунке 2.
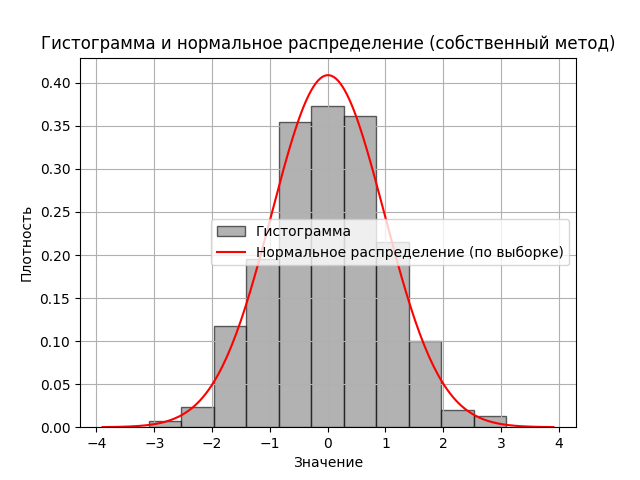
Рисунок 2 - Гистограмма для интервального вариационного ряда с параметрами, приведёнными в таблице 2
Тестирование предлагаемого алгоритма генерирования случайных чисел проводилось на примерах нормального, показательного и синусоидального распределений. Интегральнаяфункціяраспределения для нормированного нормального закона с математическим ожиданием, равным нулю, и среднеквадратичным отклонением,равным единице, имеет вид :
Случайные числа, подчиняющиеся распределению (5), вычислялись по формуле (4) с использованием разработанной программы на выборках с объёмом n=1000 в диапазоне случайных чисел [-5, 5], который содержит более 99,998% от всех случайных чисел, подчиняющихся формуле (5) . Сгенерированная выборка представлялась в виде интервального вариационного ряда, приведённого в таблице 2. Количество интервалов вычислялось по формуле Стерджесса s=1+3,322lоg10(1000) с последующим округлением до ближайшего большего нечётного числа, которое в данном случае равнялось 11.
Вычисленное среднее выборочное хср=0,05 и среднее выборочное отклонение sср=1,02 хорошо согласуются с математическим ожиданием M(x)=0 и средним квадратичным отклонением σ=1 для используемой интегральной функции распределения.
Проверка гипотезы о соответствии выборки нормальному закону проверялась с помощью χ2- критерия Пирсона (1). Плотность нормального распределения вычислялась по формуле (3) в точке xсрi, отвечающей координате середины i-го интервала. Значение χ2 для выборок с различной стартовой точкой изменялся от 3,0 до 10,1, но всегда был меньше критической величины, которая для 8 степеней свободы при 5%-м уровне значимости равняется 15,5 . Поэтому нулевая гипотеза о нормальности сгенерированной выборки принимается.
Дополнительные тестовые испытания проводились на примере показательного закона распределения с математическим ожиданием M(x)=1 и среднеквадратичным отклонением σ, равным 1,
и в случае синусоидального закона с математическим ожиданием M(x)=π/2 и среднеквадратичным отклонением σ, равным π/2:
Плотность показательного распределения определяется формулой
Дифференциальная функция синусоидального закона имеет вид
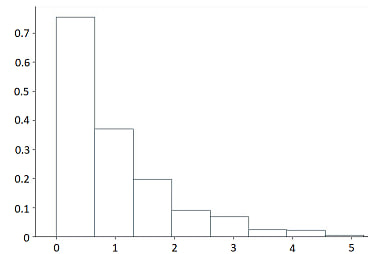
Рисунок 3 - Гистограмма для показательного закона распределения
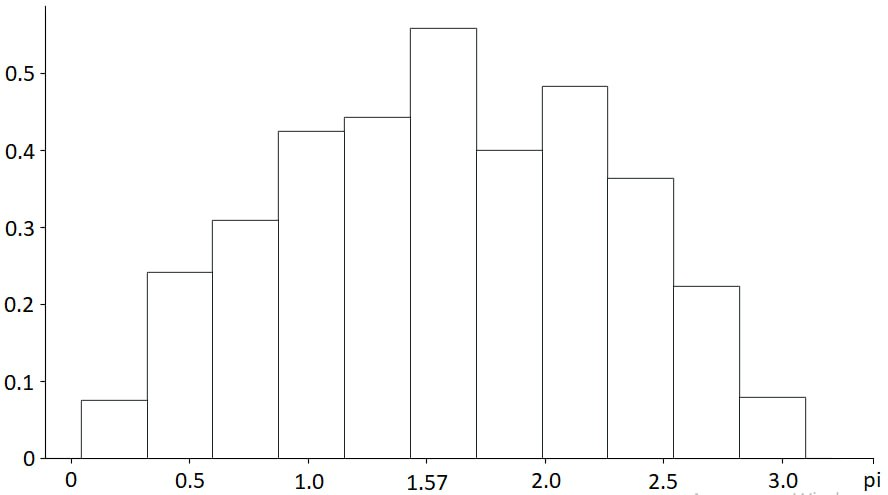
Рисунок 4 - Гистограмма в случае синусоидального закона распределения
- показательное распределение: выборочное среднее равно 0,99, средневыборочное отклонение равно 0,98;
- синусоидальное распределение: выборочное среднее равно 1,5.
Полученные выборочные параметры хорошо согласуются с математическими ожиданиями и среднеквадратическими отклонениями для соответствующих интегральных функций распределения. Поэтому можно говорить о том, что анализируемые выборки в данном случае также подчиняются заданным функциям распределения.
3. Обсуждение полученных данных
Тестовые испытания позволяют сделать вывод, что предлагаемый алгоритм обеспечивает генерирование адекватной выборки для произвольных интегральных функций распределения. Алгоритм метода может быть легко реализован на любом алгоритмическом языке при наличии генератора случайных целых чисел. Затрачиваемое машинное время в тестовых испытаниях для получения выборок с объёмом до 105 на обычных компьютерах средней мощности не превышает 30 секунд. Точность генерирования случайных величин определяется максимальным значением N, которое определяется используемым целочисленным генератором, и точностью вычисления интегральной функции распределения.
При необходимости генерирования случайных чисел в соответствии с наиболее часто используемыми распределениями (нормальное распределение, распределение Стьюдента и т.д.) можно воспользоваться стандартными функциями или программами, предлагаемыми в интернете, если они вызывают доверие. Предлагаемый алгоритм полезен в случае анализа процессов с неизвестными функциями распределения. Подобные случаи, например, встречаются при обработке результатов мониторинга территории ветровых электростанций (ВЭС) и прилегающих к ним зонам.
Рассмотрим следующий пример. Во многих странах оценка влияния ВЭС на орнитокомплексы проводится в соответствии с рекомендациями Шотландского фонда природного наследия . Согласно этим рекомендациям, при организации мониторинговых мероприятий предлагается выделить несколько участков, где будут проводиться наблюдения за птицами. Полученная информация затем экстраполируется на всю территорию ВЭС.
Проведём анализ влияния общей площади выбранных участков на точность экстраполированных данных на примере ветрового парка «Приморск-1» . Предположим, что выборочные данные подчиняются нормальному закону распределения. Площадь территории станции S примерно равна 10,1 км2. Общая площадь участков наблюдения составляла около s=2,59 км2. Для генерирования случайных величин можно воспользоваться нашим методом или встроенной функцией на одном из алгоритмических языков .
Численность птиц, зарегистрированных на всём участке в 2017 году за t=24 дня наблюдения, составило 5923 особей всех видов или 247 птиц в расчёте на один день. Умножая приведённые данные на S/s≈3,9, найдём следующие экстраполированные значения: общая численность птиц на всей территории ветрового парка - 23097 особей, среднее значение в расчёте на один день – 963.
На первый взгляд может показаться, что полученные данные хорошо характеризуют истинное положение. В действительности, для более корректной экстраполяции необходимо учесть ряд обстоятельств, которые не укладываются в предположение о нормальности распределения. Например, общая площадь участков, где проводился учёт, состояла из трёх делянок, которые размещались в различных местах на территории ветрового парка с неравномерным распределением птиц, что в данном случае приведёт к более высокому значению дисперсии.
Оценка вклада неравномерности может быть проведена с использованием нестандартной интегральной функции распределения, которая учитывала бы направление полёта зарегистрированной птицы. Обсуждение других причин, связанных с невыполнением предположения о нормальности распределения, выходит за рамки тематики настоящей работы.
4. Заключение
В заключение отметим, что вся необходимая информация о динамике орнитокомплексов на территории ветровых парков Приморск-1, Пиморск-2 и Ботиевской ВЭС содержится в доступных отчётах, поэтому имеются все условия для проведения соответствующего статистического анализа с использованием разработанного метода.
