FUNCTION APPROXIMATION WITH THE USE OF THE REMEZ ALGORITHM
FUNCTION APPROXIMATION WITH THE USE OF THE REMEZ ALGORITHM
Abstract
The article examines one of the methods of function approximation – the Remez algorithm. It is designed to find a polynomial that best approximates a given function on a certain interval. The algorithm finds the polynomial that minimizes the maximum error between the given function and the polynomial approximation. The algorithm finds application in various fields of science and engineering. The work gives the Remez algorithm directly, an example of using the algorithm in solving the problem of function approximation, and analyses the accuracy of the obtained result. The specific feature of this article is the construction of graphs of the approximated function and the polynomial of the best approximation, as well as obtaining the value of the approximation error of the function, in the interactive geometric environment "GeoGebra", mainly used for solving problems of school mathematics and rarely used for solving those of higher mathematics. The information presented in the article can be useful for students and researchers interested in the problems of function approximation.
1. Введение
В науке и технике часто имеется набор значений данных, полученных путем выборки или эксперимента, которые представляют значения функции для ограниченного числа значений независимой переменной. Часто требуется интерполировать, то есть оценить значение этой функции для промежуточного значения независимой переменной. Тесно связанной проблемой является аппроксимация сложной функции простой функцией. В некоторых ситуациях формула для некоторой заданной функции известна, но слишком сложна для эффективной оценки. Несколько точек данных из исходной функции могут быть интерполированы для получения более простой функции, которая все еще довольно близка к оригиналу. Результирующий выигрыш в простоте может перевесить потери от ошибки интерполяции и повысить производительность процесса вычисления. Одним из эффективных методов аппроксимации функций является алгоритм Ремеза .
Алгоритм Ремеза предназначен для нахождения многочлена, наилучшим образом приближающего заданную функцию на определенном интервале. По существу, алгоритм находит такой многочлен, который минимизирует максимальную ошибку между заданной функцией и многочленной аппроксимацией. Хотя алгоритм Ремеза не всегда гарантирует нахождение лучшей возможной аппроксимации, он часто дает близкую аппроксимацию. Алгоритм Ремеза находит применение в различных областях науки и техники , , а особенно полезен в численном анализе и обработке сигналов , , , где аппроксимация функций – обычная задача.
Алгоритм Ремеза претерпел ряд модификаций и усовершенствований с момента его представления Ремезом в 1934 году. Однако, несмотря на различные модификации, алгоритм Ремеза остается важным инструментом для аппроксимации функций в математике и инженерии. Понимание алгоритма Ремеза и его различных применений требует знакомства с численным анализом и теорией оптимизации. Тем не менее с его различными преимуществами и применениями, алгоритм Ремеза остается увлекательной темой для исследователей и математиков. Цель этой статьи – представить обзор алгоритма Ремеза, включая его основные принципы, применение при аппроксимации функций.
2. Понятие многочлена наилучшего приближения
Для ясности работы алгоритма Ремеза определимся с понятием многочлена наилучшего приближения. Воспользуемся следующим определением .
Пусть для непрерывной функции, заданной на отрезке нужно найти многочлен наилучшего приближения
, то есть
Однако найти многочлен наилучшего приближения в пространстве в общем случае затруднительно. Поэтому на практике находится многочлен
«почти» наилучшего приближения, то есть многочлен, для которого
Алгоритм Ремеза, который будет описан ниже, позволяет построить последовательность многочленов таких, что
Перейдем к описанию алгоритма Ремеза .
3. Алгоритм Ремеза
Суть алгоритма, предложенного в 1934 году Е.Я. Ремезом , сводится к выполнению следующих шагов .
1-й шаг. Выбор начального альтернанса.
На отрезке выбираем
равноудаленные точки
, являющиеся Чебышевским альтернансом.
Для этого необходимо и достаточно, чтобы разность принимала в точках
значения равные по абсолютной величине, но чередующиеся по знаку:
Для ускорения сходимости обычно выбирают точки Чебышевских узлов
2-й шаг. Построение многочлена наилучшего приближения по заданному альтернансу.
На следующем шаге по последовательности строим многочлен
степени не выше
, являющийся многочленом наилучшего приближения на заданном множестве точек
.
Из теоремы Валле-Пуссена следует выполнение неравенства , где
– величина наилучшего приближения, а
– искомый полином наилучшего приближения степени не выше
. Кроме того выполняется неравенство
, где
– величина наилучшего приближения. При этом по теореме Чебышёва, если
, то выполняется равенство
и построение завершено (3-й шаг, проверка на остановку).
4-й шаг. Выбор нового альтернанса.
Если условие не выполняется, то по многочлену
и последовательности
строим новую последовательность
так, чтобы выполнялись условия
Для того чтобы удовлетворить этим условиям, достаточно заменить одну из точек на
точку, в которой реализуется условие
. На практике следят за тем, чтобы на каждом шаге новый набор узлов был упорядочен по возрастанию и таким, чтобы на новом упорядоченном множестве выполнялось условие чередования знаков
. На практике, для ускорения сходимости, желательно как можно больше точек из
заменить новыми так, чтобы
были возможно большими.
Описанная выше процедура повторяется до тех пор, пока не будет получен искомый многочлен наилучшего приближения, или пока не будет выполняться неравенство
4. Пример работы алгоритма Ремеза
Рассмотрим следующий пример. Пусть задана кусочно-линейная функция
Построим для заданной функции полином наилучшего приближения второго порядка. Получение полинома первой степени вы можете нейти в пособии Иродовой И.П. .
В качестве начального альтернанса выберем в точки .
Построим по этим точкам интерполяционный многочлен второй степени , исходя из условий
Учитывая, что для нахождения неизвестных приходим к системе линейных уравнений
из которой находим
Так как построенный многочлен нелинейный, то для отыскания
необходимо исследовать
на наибольшее значение на каждом из подынтервалов исходной функции.
Таким образом, остается проверить точки . Последовательно находим
Так как , то полиномом наилучшего приближения второй степени для заданной функции является полином
, а величина наилучшего приближения
. На рисунке 1 представлены графики аппроксимируемой функции и полинома наилучшего приближения, построенные в интерактивной геометрической среде «GeoGebra». Величина наилучшего приближения, найденная в ИГС «GeoGebra», составляет 0,875, что совпадает со значением, полученным нами аналитическим путем.
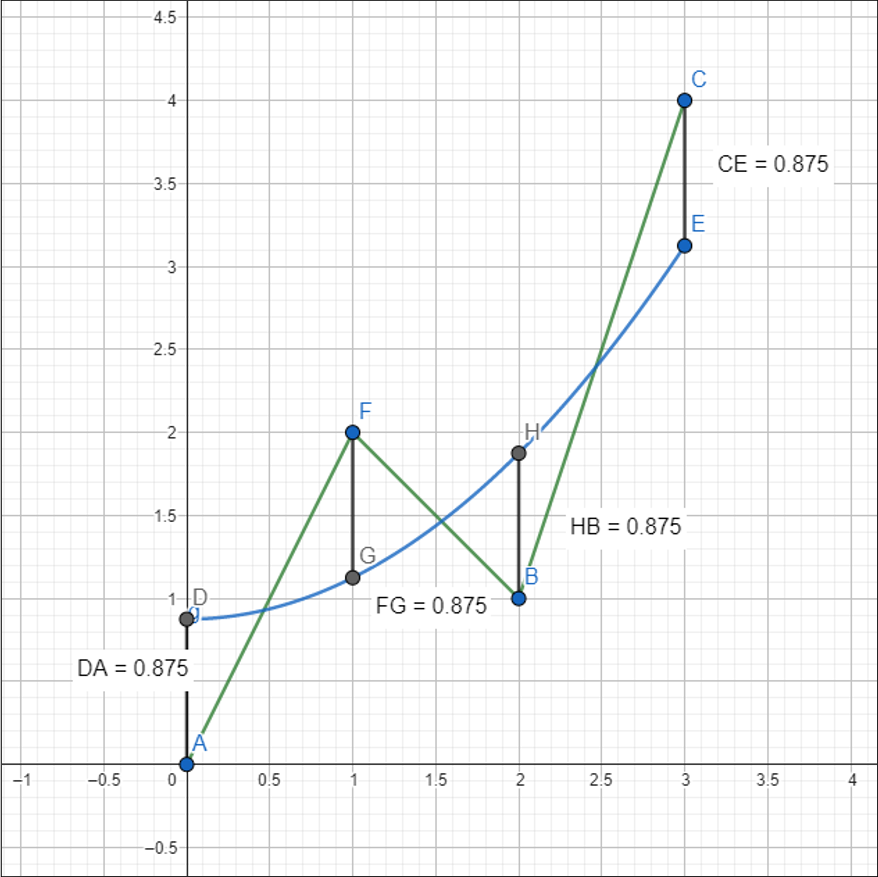
Рисунок 1 - Заданная функция и её полином наилучшего приближения
5. Заключение
В заключение можно сказать, что алгоритм Ремеза является мощным инструментом для решения задач аппроксимации функций. Он может использоваться в различных областях науки и техники, таких как обработка сигналов, оптимизация производительности систем, создание математических моделей и т.д.
Можно выделить следующие преимущества алгоритма Ремеза:
- высокая точность при приближении функций на заданном интервале;
- быстрота вычислений: многочлены, полученные с помощью алгоритма Ремеза, могут быть легко вычислены на компьютере;
- универсальность: алгоритм Ремеза может применяться для любой функции, определенной на заданном интервале;
- адаптивность: если входные данные изменяются, алгоритм Ремеза может быть легко приспособлен к новым значениям;
- простота: алгоритм Ремеза имеет простой и интуитивно понятный алгоритм, который может быть легко реализован в программном обеспечении.
Однако следует учитывать также и недостатки алгоритма Ремеза:
- алгоритм Ремеза требует грамотного выбора начального приближения, которое влияет на точность решения. Неправильный выбор начального приближения может привести к неадекватным результатам;
- высокая вычислительная сложность: алгоритм Ремеза требует выполнения большого количества вычислений, которые могут быть ресурсоемкими для компьютера или мобильного устройства;
- требуется аппроксимация функции многочленом: алгоритм Ремеза работает только для функций, которые могут быть представлены в виде многочленов. Для функций, которые не могут быть аппроксимированы многочленами, требуются другие методы.
Тем не менее все эти недостатки не могут оспорить значимости алгоритма Ремеза в научных и инженерных приложениях. С его помощью можно существенно улучшить точность математических моделей. И в этом смысле алгоритм Ремеза является неотъемлемой частью современных технологий и инструментария науки и техники, а знакомство с ним и его использование рекомендуется для всех, кто занимается смежными науками.
