METHODOLOGY OF CREATIVE THINKING BASED ON A CONSCIOUS SEARCH FOR PROBLEM-SOLVING

Философы одержали «пиррову победу»: добились исключения математики из цикла обязательных для их специальности дисциплин с 2021 года, обосновав это отсутствием интереса студентов к этому предмету. В результате выпускникам философских факультетов будут не доступны в полном объеме ни «Тэатет», ни «Менон» Платона, ни парадоксы Зенона, ни трактат «О небе» Аристотеля. Без знания принципа Ферма непонятен Декарт, без понимания бесконечно-малого – Лейбниц, без аксиоматического метода – «Критика чистого разума» Канта, без актуальной бесконечности – Спиноза и «Наука логика» Гегеля, без дифференциального исчисления неясен Маркс, без булевой алгебры – Пирс, без теории множеств – логическая реформа Рассела и все ее бесчисленные последствия, без теории функций – Гуссерль, без теории групп – Кассирер. «Кто-то из перечисленных философов был великим математиком, как Декарт или Лейбниц. Кто-то был по образованию математиком, как Кант или Гуссерль. Кто-то изучал математику долго и подробно, как Кассирер и марбургские неокантианцы. Чтобы их понимать, надо хорошо себе представлять, как они думали, а ведь думали они математическими моделями. … Философам нужно преподавать ту математику, которая нужна философам. Тогда все разговоры о «ее нерелевантности для философского образования» отпадут сами собой. Тогда у студентов-философов будут гореть глаза, и они смогут все преодолеть, и курс математики, наконец, перестанет вызывать у них устойчивую аллергическую реакцию» (Губайловский В.А.).

Я поделюсь далее своим опытом преподавания математики – как философам, так и студентам других факультетов Саратовского университета, которые оценивают мои усилия максимальным рейтингом по 6 характеристикам (способность донести материал, сложность сдачи экзамена, практическая польза предмета, увлекательность предмета, использование наглядных и технических средств бучения, чувство юмора). Покажу, как с помощью осознанного поиска стратегии решения даже простых задач можно приобщить не только философов к наслаждению от ощущения гармонии рационального, и одновременно творческого, мышления.

Разумеется, я опираюсь на достижения многих учёных, философов, психологов, педагогов и популяризаторов науки (А.Н. Уайтхед [6], Д. Пойя [4], Г.П. Щедровицкий, В.В. Давыдов; Я. И. Перельман, М. Гарднер, Н.Н. Андреев [2], [3] и др.), а также на собственный опыт разработки и применения технологии проблемно-деловых игр [5], [7], [8] во многих организациях страны вместе с командой саратовских учёных, философов, психологов, математиков, управленцев, экономистов, юристов – для решения социально-экономических проблем, осуществления инноваций и повышения эффективности процессов обучения.

Начну с вроде бы чисто геометрической задачи, но в предлагаемой мной методологической интерпретации, которая может быть легко использована для развития навыка аналитического мышления в любой сфере деятельности.

Задача 1. Исходно даётся квадрат из 9 точек (рис. 1):

Рисунок 1 - Квадрат из 9 точек

DOI:10.23670/IRJ.2022.123.64.1

Прямыми в этой задаче будем считать только те, которые проходят точно через 3 точки; – таких, здесь, очевидно, 8 (рис. 2):

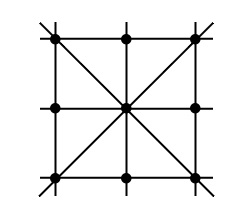
Рисунок 2 - Расположение прямых

DOI:10.23670/IRJ.2022.123.64.2

Нужно переместить две точки так, чтобы «тройных» прямых стало 10. Я сразу предлагаю аудитории не заниматься поиском решения «методом тыка» (тем более, что решение кому-то уже может быть известно, или моментально придёт в голову), и объясняю, что моё задание – не в нахождении решения, как такового, любым способом, а – в создании метода анализа этой ситуации, выводящего на стратегию выявления тех точек, которые оптимальны для перемещения; после чего, также аналитически рассуждая, выявить оптимальные направления их перемещения; то есть я превращаю эту задачу-развлечение в осознанную отработку общей технологии аналитического мышления.

Первым шагом на этом пути (степень и форма подсказки зависит от уровня аудитории) будет поиск критерия классификации имеющихся в проблемной ситуации объектов; в данном конкретном случае – это 9 точек. Очевидный критерий здесь – сколько каждая точка несёт на себе «тройных» прямых, ибо её передвижение означает потерю этих линий, а нам нужно число их даже увеличить на 2! В результате анализа по такому критерию получаем 3 типа точек: центральная, несущая 4 прямых; 4 угловых, несущих по 3 прямых; и средние 4 точки, несущие по 2 прямых.

Естественно, приходим к выводу, что двигать надо 2 средних. Направления движения тоже не равноценны, – легко обнаруживаем, что есть оптимальное – по средней линии квадрата, которое сохраняет одну из потенциально теряемых прямых. В результате этого двухступенчатого анализа ситуации быстро приходим к решению (рис. 3):

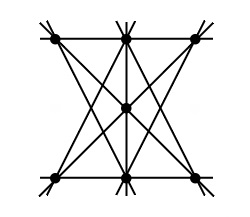
Рисунок 3 - Решение задачи

DOI:10.23670/IRJ.2022.123.64.3

Дальше, для закрепления навыка анализа, я обычно даю весьма похожую задачу (увы, результат не всегда бывает сразу успешным):

Задача 2. Имеется опять квадрат, но уже из 8 позиций – 8 кучек спичек по 3 в каждой (центральная позиция здесь отсутствует, рис. 4):

Рисунок 4 - 8 кучек спичек по 3 в каждой

DOI:10.23670/IRJ.2022.123.64.4

Сумма спичек по каждой из сторон квадрата равна 9. Сохраняя число и расположение кучек, но имея возможность перекладывать спички из кучки в кучку, нужно доложить в них ещё 4 новых дополнительных спички так, чтобы суммы числа спичек по сторонам квадрата опять давали число 9. Классифицируя 8 имеющихся объектов (кучек) опять по критерию несения содержательной нагрузки (в данном случае числовой нагрузки), учащиеся должны увидеть, что угловые кучки считаются дважды, в то время как средние, лишь один раз. Отсюда следует вывод, что надо загружать спичками средние позиции, а угловые, наоборот, разгружать; тогда решение получается довольно быстро (рис. 5):

Рисунок 5 - Решение задачи 2

DOI:10.23670/IRJ.2022.123.64.5

Ещё один пример, скорее, физического, чем математического характера:

Задача 3. подходят одновременно к движущемуся эскалатору (неважно вверх или вниз) два человека, и начинают идти по нему – один быстро, другой – медленно. Кто из них насчитает больше ступеней? Обычно предлагают все варианты ответа: тот, кто быстрее; тот, кто медленнее; одинаковое количество. Каждый путано пытается объяснить своё решение. Я предлагаю им так модифицировать ситуацию, чтобы условия задачи сохранились, но решение было бы очевидным даже ребёнку. Иногда догадываются: тот, кто идёт медленнее, может сделать всего один шаг, насчитав, естественно, лишь одну ступеньку; второй же делает, по крайней мере, хотя бы ещё один шаг, и тогда очевидно, что он всегда насчитает больше ступеней.

Эта задача может быть проинтерпретирована как иллюстрация методологического приёма сведения проблемы (наверное, не всякой) к такой «предельной» форме (но с сохранением всех основных характеристик ситуации), когда её решение становится очевидным. Пример одновременно поясняет глубокую и нетривиальную идею известного философа, логика и математика А. Уайтхеда [6, С. 376]: «Философия есть критика абстракций, управляющих конкретными разновидностями мышления. Из этого следует, что философия в собственном смысле данного термина не может быть доказательной, ибо доказательства базируются на абстракциях. Философия либо самоочевидна, либо это не философия. Попытки любого философского дискурса должны быть направлены на создание самоочевидности».

В следующей задаче этот приём упрощения тоже работает.

Задача 4. По окружности располагаются равномерно любое количество предметов («точек» на доске, листе бумаги или того, что может оказаться под рукой – камешки, монетки, кусочки веточек, чего угодно). Играют двое, снимая по очереди либо один, либо два соседних (относительно исходного расположения) предмета. Выигрывает тот, кто берёт последним. Требуется найти выигрышную стратегию, независимую от числа предметов.

Наличие такой стратегии следует из соответствующей теоремы для конечных игр с полной информацией, к каковым относятся, например, шахматы. Но в шахматах, в силу огромного числа комбинаций, человеку практически невозможно реализовать выигрышную стратегию, которая теоретически всегда существует для белых фигур. В игре Задачи 4 такую стратегию можно найти и всегда осуществлять для любого числа предметов!

Какие методы из перечисленных выше здесь можно применить и освоить? Понятно, что при наличии двух-трёх десятков предметов число вариантов поочерёдных ходов будет слишком большим для того, чтобы предвидеть исход игры. Рассмотрим аналогичную упрощенную задачу с минимальным числом предметов, которых должно быть 3. Тогда, сколько бы ни взял первый игрок (1 или 2 предмета), второй забирает остальное и выигрывает. Следующий по возрастанию сложности вариант – 4 предмета. В этом случае легко обнаруживается, что выигрывает всегда второй, в том числе, и тогда, когда первый берёт лишь один предмет, но только тогда, когда второй забирает противоположный ему предмет, создавая симметричную ситуацию, финал которой всегда за ним. Эта стратегия, будучи обобщенной на любое число предметов, оказывается всегда выигрышной для второго игрока, то есть, после первого хода начинающего второй должен взять с противоположной стороны круга 1 или 2 предмета так, чтобы он оказался разделённым на две симметричные части с одинаковым числом предметов в каждой. Тогда на любой ход первого второй зеркально снимает с противоположной симметричной половины столько же предметов; очевидно, он всегда сделает последний выигрышный ход!

Таким образом, в процессе поиска решения этой задачи (как и многих других) осваиваются эвристические методы: аналогии, упрощения, вспомогательной задачи, индукции и обобщения. Кроме того, в чём состоит ещё один существенный аспект моего предложения – это применение опыта проблемно-деловых игр (ПДИ), которые опираются на сюжетно-игровую концепцию реальности [8], [9]. ПДИ основательно разработана и как методология, и как социальная технология, и как совокупность техник и многократно описана – в разных аспектах авторами, большинство которых философы, а также психологи, инженеры, экономисты, математики, ставшие специалистами нового профиля – организаторами коллективной мыследеятельности. Наиболее полно представление авторов о ПДИ выражено в коллективном труде [5] под редакцией инициатора и наиболее активных членов творческой группы: О.В. Шимельфенига, В.Н. Южакова, Т.П. Фокиной.

Основным техническим содержанием процесса является чередование групповой работы «игроков», заслушивание и обсуждение докладов от групп на общих собраниях (конференциях), а также оформление письменных материалов (документов) игры; нередко по результатам игры составляется уже после неё обстоятельный «итоговый документ» и подписывается приказ о назначениях на ответственные должности. Как показывает само название, авторы новой социальной технологии определили её место в ряду деловых игр. Действительно, многое взято из социальных технологий, известных как организационно-деятельностные игры Г.П. Щедровицкого, инновационные игры B.C. Дудченко, производственные игры М.М. Бирштейн, управленческие имитационные игры В.Ф. Комарова и т.п. Саратовская технология, относясь к классу деловых игр (business-games), получила характеристику «проблемная» соответственно своей направленности – прежде всего на исследование социально-экономической проблемной ситуации, в которой оказалась данная организация. С этим связаны особенности ПДИ: высокий уровень методологической, социологической и культурологической рефлексии (это определяется составом методологов), сложная структура игры (исследование проблемного поля, «идеальная» модель решения, «погружение» этой модели в реальность, наработка конкретных путей решения проблем); целенаправленная работа на разрушение традиционных стереотипов мышления («антиконцепция») и психологическими техниками усиления внимания к проблемным узлам ситуации («провокации» игротехников типа «вызываю огонь на себя»), и т.д. Следует отметить, что именно форма игры, во многом, и дала возможность пробуждаться творческому потенциалу сотрудников и руководителей многочисленных организаций, с которыми мы работали на протяжении ряда лет.

Опыт проблемно-деловых игр можно применять в процессе нахождения стратегий решения задач и в обучении любой дисциплине, – разбивая группу учащихся на команды, каждая из которых ищет решение. В таком интерактивном процессе используется также и технологии ТРИЗ (Теория Решения Изобретательских Задач: мозговой штурм, синектика и др.) [1], что в целом одновременно развивает у участников компетенции из области soft skills: убедительно аргументировать свою позицию; грамотно выстраивать коммуникацию; форму подачи результата; гибкость и принятие критики; креативность; управление временем; стрессоустойчивость; готовность выполнять рутинную работу; лидерские качества – умение принимать решения, сформировать команду, разрешать конфликты. А в заключение, анализируя совместно действия каждого и деятельность групп, можно дать ещё и уроки философской рефлексии.

Разумеется, почти все приводимые здесь задачи обычно легки для знающих математику и тех, кто с ней тесно связан (для них можно подбирать более сложные проблемы), я же просто иллюстрирую предлагаемый мною комплексный подход к развитию у учащихся всех возрастов и профилей многообразных способностей, методов и навыков с помощью достаточно простых задач.

Задача 5. (Из старинных, как и следующая). Крестьянин пришёл к царю и попросил: «Царь, позволь мне взять одно яблоко из твоего сада». Царь разрешил. Пошёл крестьянин к саду и видит: весь сад огорожен тройным забором, в каждом заборе есть только одни ворота, и около каждых ворот стоит сторож. Когда крестьянин проходил мимо первого сторожа, тот сказал ему: «Возьми яблоки, но при выходе отдашь мне половину яблок, которые у тебя будут, и ещё одно». То же сказали ему и другие сторожа, охранявшие свои ворота. Сколько яблок должен взять крестьянин, чтобы, отдав положенные части трём сторожам, унести домой одно яблоко?

В процессе поиска решения этой задачи, кроме перечисленных выше методов ТРИЗ и философской рефлексии (которые можно отрабатывать на всех проблемах), можно усвоить такие эвристические приёмы, как: работа от конца к началу; разложение исследуемого на части; аналогию; упрощение; синтез блоков.

Действительно, концом этого сюжета будет отдача первому сторожу (который станет последним в серии отдач) его доли, после чего у крестьянина должно остаться одно яблоко. Легко посчитать, что для выполнения этой финальной операции у него должно быть 4 яблока: половину (это 2) плюс 1 отдаются сторожу и у него остаётся, как раз, одно яблоко. Отсюда следует, что после выхода из предыдущих вторых ворот ему надо иметь эти самые 4 яблока. А это означает, что на подходе ко вторым воротам у него должно быть 10 яблок: 5 + 1 он отдаёт сторожу и 4 оставляет себе. Аналогичные рассуждения приводят к тому, что сорвать ему придётся 22 яблока, поскольку придётся отдать сначала 11 + 1, чтобы остались нужные 10 для вторых ворот.

Кстати, при рефлексии над процессом решения этой задачки можно заметить, что она является также примером коррупции и откатов на госслужбе, причём откат средний: 50% + 1; бывает и больше.

Следующая задача, в определённом смысле, является упрощенным вариантом предыдущей, и поэтому может быть использована для проверки и закрепления приобретённых навыков.

Задача 6. Три крестьянина остановились на постоялом дворе, заказали хозяйке сварить им картошки и от усталости заснули. Пока они спали им принесли заказанное. Первый проснувшийся съел треть из имевшихся картофелин и опять заснул. Второй проснувшийся, увидев еду, тоже съел треть и заснул. Проснувшийся третий съел тоже треть. Когда, наконец, все проснулись, то увидели 8 оставшихся картофелин. Кому из них сколько досталось?

Очевидно, разумно начинать также с конца, то есть, раз третий проснувшийся оставил двоим 8 картофелин (по 4 каждому), значит, он съел тоже 4 – третью часть от увиденных, очевидно, им 12. Предыдущий, следовательно, съел 6 – третью часть от увиденных 18 картофелин, а самый первый, таким образом, должен был увидеть 27 картошек, из которых съел третью часть – 9 штук.

Следующая группа задач приводит нас к необходимости преодоления стереотипов мышления, расширения кругозора, саморефлексии, то есть, к более творческому и философскому отношению к реальности.

Задача 7.

Найти два числа X и Y, удовлетворяющие условию:

X + Y = X Y = X : Y

Задача 8.

9 точек образуют квадрат. Требуется соединить их все 4-мя отрезками, не отрывая карандаша от бумаги, и не проводя два раза по одной и той же линии (рис. 6):

Рисунок 6 - Квадрат из 9 точек

DOI:10.23670/IRJ.2022.123.64.6

Хотя обе задачи не требуют знаний выше начальных классов, обычно не решаются сразу практически в любой аудитории. Вот решение Задачи 7:

 X = 1/2, Y = - 1: ½ + (- 1) = ½ . ( - 1) = ½ : ( - 1) = - ½. 

А вот и решение Задачи 8 (рис. 7):

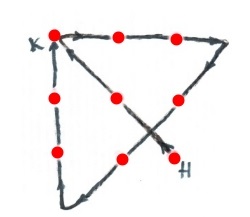
Рисунок 7 - Решение задачи 8

DOI:10.23670/IRJ.2022.123.64.7

В чём же состоит главная трудность в поисках ответа на эти задания?

– В ограничениях, которые мы сами себе автоматически устанавливаем, вопреки известной юридической максиме: «То, что не запрещено, – разрешено». Решение первой задачи обычно ищут в целых положительных числах, а во второй, – не выходя за пределы квадрата. Но кто ввёл эти запреты? – Наше подсознание – внутренний тюремщик.

Высокий уровень аналитического мышления требует развития ещё такого, например, тонкого различения пребывания какого-то объекта в двух частично «пересекающихся» множествах, которые смешиваются многими поверхностными исследователями, порождая неадекватные восприятия и модели реальности. Эта сложная логическая коллизия может быть легко проиллюстрирована старинной русской загадкой (естественно, с последующим её разбором): «Хожу я головой, хотя и на ногах; хожу я босиком, хотя и в сапогах». Ответ довольно точный, без заумных, невероятных и натянутых метафор: «Гвоздь в сапоге». А трудность его нахождения, как раз, и заключается в том, что этот самый гвоздь фигурирует в двух различных, но тесно взаимодействующих системах: человека и его сапога.

Одно из важнейших направлений повышения философского уровня восприятия реальности – это развитие навыков рефлексии – самонаблюдения, отслеживания своих автоматических шаблонов мышления и поведения. C одной стороны, это высший пилотаж – попытка реализации древнейшей максимы «Познай самого себя», а, с другой, начинать учить этому можно с помощью простейших деловых игр, например «Незнакомая планета», которая занимает очень мало времени и может быть вставлена, как передышка, в занятие по любой теме. Участники делятся на 2 группы: космонавты и аборигены; первые прилетают ко вторым и общаются с ними несколько минут, в течение которых они должны определить два закона общения аборигенов (закон 1– на все вопросы отвечают только – Да или Нет; закон 2 – если вопрос задан с улыбкой, то отвечают Да, без улыбки – Нет). Первый закон открывают, разумеется, быстро, а трудность выявления второго связана, как раз, с отсутствием навыков самонаблюдения в массовой культуре, ибо для его обнаружения следить надо не только за объектом наблюдения, но и за самим собой.

А вот старинный кейс из суфийской практики, решение которого требует применения редкого креативного эвристического приёма из технологии ТРИЗ – «принципа посредника» – на время присоединить к объекту другой, легко удаляемый объект.

Задача 9. Суфийский Мастер завещал после своей кончины трём своим ученикам 17 верблюдов, наказав разделить их между ними в такой пропорции: первому ученику – половину, второму – треть, третьему – девятую часть.

Очевидно, что задача с условием сохранения физической целостности животных простым арифметическим делением не решается. И в завещании было сказано, что тот человек, который поможет им решить задачу деления наследства, станет их новым Учителем.

Они долго ходили по свету, пока не встретили того, кто пошёл к своему сараю, вывел одного своего верблюда, присоединил к их 17, после чего первый ученик забрал своих 9 животных, второй – 6, а третий – оставшихся двоих, из которых одного чужого верблюда вернул хозяину.

Следующий кейс из суфийской традиции направлен на развитие критического мышления и улавливания тонких логических ошибок или специально организованных обманов.

Задача 10. «Жили некогда три странствующих дервиша. Однажды поздней но­чью они прибыли в караван-сарай и спросили комнату для себя и место в конюшне для своих ослов. Хозяин караван-сарая к этому времени уже спал, и дежуривший но­чью слуга отвел ослов в стойло, а дервишам предоставил комнату для ночлега за пят­надцать серебряных дирхемов. Дервиши тут же выплатили требуемую сумму вперёд.

На следующее утро хозяин понял, что с дервишей по ошибке взяли слишком много; их плата должна была составлять только десять дирхемов, и он велел слуге вер­нуть им пять дирхемов.

Слуга был не слишком честен и, кроме того, решил, что разделить пять дирхе­мов на троих будет сложновато. «Чтобы дервиши не перессорились, – подумал он, – я верну им только три дирхема, а два оставлю себе». Так он и поступил, и получилось, что дервиши потратили на ночлег только двенадцать дирхемов.

Это означало, что с дервишей взяли двенадцать дирхемов, и два дирхема при­карманил слуга: всего получается четырнадцать дирхемов. Но ведь вначале было пятнадцать дирхемов. Куда девался еще один дирхем?

Многие люди, встретившись с этой задачей, полагают, что один дирхем каким-то образом испарился. Но ведь такого быть не может, не так ли?»

Понятно, что в данном описании ситуации скрыта где-то логическая ошибка, но, как я не раз убеждался, точно указать на вводящие в заблуждение слова многим не удаётся. Поэтому задачи такого типа являются прекрасной тренировкой в компетенциикритического рационального мышления. Действительно, не так уж легко обнаружить всего лишь одно слово в одну букву – союз «и», в первой строке предпоследнего абзаца задачи, который и оказывается мошенническим орудием, поскольку заставляет дублировать 2 дирхема, прибавляя их к 12, в которых они уже один раз содержатся! Когда этот логический трюк раскрыт, всё встаёт на свои места: 10 дирхем в итоге получил хозяин, 2 прикарманил слуга и 3 вернулись дервишам, – такова судьба всех 15 дирхемов, участвовавших в этом сюжете.

Полагаю, что рассмотренная выше дюжина проблемных сюжетов достаточно убедительно продемонстрировала возможности математики в формировании аналитического рационального и одновременно творческого мышления в нескучной поисково-игровой форме. На самом деле, любую математическую дисциплину можно в той или иной степени подавать таким проблемно-ориентированным способом.