COMPUTER SIMULATION OF THE KINETICS OF THERMAL PROCESSES IN THE CELL DISC BRAKES

Миронов Д. О.

Aспирант, Федеральное государственное бюджетное образовательное учреждение высшего образования "Московский государственный университет путей сообщения Императора Николая II"

 КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ КИНЕТИКИ ТЕПЛОВЫХ ПРОЦЕССОВ В ЭЛЕМЕНТАХ ДИСКОВОГО ТОРМОЗА

 Аннотация

В статье приведены результаты компьютерного моделирования кинетики тепловых процессов в элементах дисковых тормозов. При этом выполнены исследования нестационарных температурных полей с допущением о постоянстве распределения давлений во времени на поверхности торможения. Для конечно-элементной модели со слабым отклонением от осевой симметрии при достаточной для вступления в силу граничных условий длительности подвода тепловой мощности получено поле температур практически близкое к осесимметричному, что удовлетворяет условию дальнейшего равномерного подвода теплоты в окружном направлении и доказывает правомерность использования схемы осесимметричного теплового нагружения в такой схеме.

Ключевые слова: дисковый тормоз, компьютерное моделирование, тепловые процессы.

Mironov D. O.

Postgraduate student, Moscow state University of railway engineering

COMPUTER SIMULATION OF THE KINETICS OF THERMAL PROCESSES IN THE CELL DISC BRAKES

Abstract

The article presents the results of computer simulation of the kinetics of thermal processes in the elements of disc brakes. This made the study of unsteady temperature fields with the assumption of the constancy of the pressure distribution in time for the braking surface. For the finite element model with slight deviation from axial symmetry with sufficient for entry into force of the boundary conditions of thermal power supply duration to get the temperature field is almost close to the ax symmetric that satisfies further uniform heat supply in the circumferential direction and proves the legitimacy of the use of the scheme ax symmetric thermal loading in such a scheme.

Keywords: disc brake, computer simulation, thermal processes.

Важное место в расчете нестационарных температурных полей, возникающих в деталях дискового тормоза при торможении, занимает контактная задача [1-3]. Интенсивность теплового потока, выделяемого на поверхностях торможения, определяется распределением давлений между накладками и диском, и скоростью движения вагона.

Особенность контактной задачи для башмака и диска состоит в том, что определяющее влияние на законы распределения контактных давлений оказывают конструкция накладок, способы соединения колодки с башмаком, а также накладок с пластиной колодки [4]. В процессе торможения законы распределения контактных давлений могут меняться из-за температурных деформаций элементов тормоза.

В работе выполнены исследования нестационарных температурных полей с допущением о постоянстве распределения давлений во времени на поверхности торможения. Температурная задача для диска решалась в предположении постоянства температур в окружном направлении. Для ее решения могла бы использоваться осесимметричная расчетная схема, представляющая собой осевое сечение диска. Для такой схемы требуется распределение давлений в радиальном направлении.

При решении задачи задавались следующие краевые условия. По поверхности торможения – подвод и отвод тепла, по другим поверхностям – отвод тепла, для других неконтактирующих узлов – никаких специальных краевых условий не задавалось, что обеспечивало учет симметрии схемы относительно этих плоскостей. Информация о температурах и напряжениях выдавалась для узлов, расположенных в плоскости у = 0. Температура окружающей среды принималась равной 0°С.

Для проведения компьютерного моделирования кинетики тепловых процессов для элементов дисковых тормозов сделаем следующие допущения. Моделирование проводим в режиме экстренного торможения поезда, при этом максимальная конструкционная скорость тележек модели 48-6075 составляет 160 км/ч. По данным Тверского института вагоностроения коэффициент трения между накладками и венцом в процессе торможения довольно стабилен и может быть принят постоянным и равным 0,25 [5]. Другие постоянные величины принимались в соответствии с конструктивными особенностями электропоездов: радиус вагонного колеса по кругу катания – 0,475 м, для нестационарного процесса – шаг интегрирования по времени 5 с. Из анализа результатов решения максимальное значение температуры для накладок 1439°С получается на поверхности трения на 30 с, для венца максимальное значение температуры 426°С получается также для узлов на поверхности трения на радиусе 220 мм, в момент времени 43 с (рис. 1, 2).

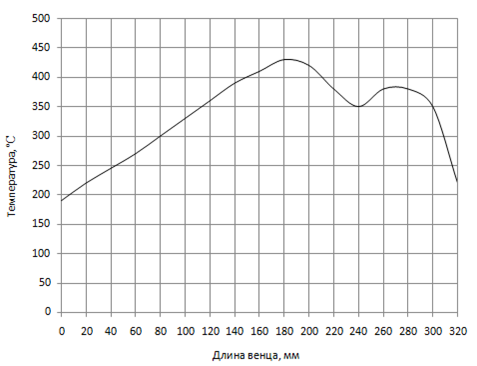
Рис. 1 - Распределение температуры по длине венца на 43 с

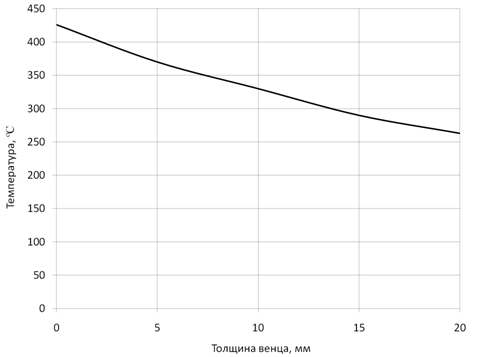
Рис. 2 - Распределение температуры по толщине венца на длине 220 мм (43 с)

 

Если мысленно представить конечно-элементную расчётную схему температурной задачи как некоторую зависимость вектора узловых температур, аргументами которой является время и вектор приведенной тепловой мощности, а конечно-элементную расчётную схему температурной задачи как зависимость вектора узловых эквивалентных температурных напряжений от аргумента – вектора узловых температур, то сопоставление исходных данных и результатов расчёта может дать представление о характере этих зависимостей.

Построим распределение силовой составляющей приведенной тепловой мощности и распределение температур вдоль радиуса, проходящего через центр кольцевой проточки под разрезные кольца, в моменты времени 20, 43 и 80 с (рис. 3). Прослеживается сходство между видом силовой составляющей приведенной мощности и распределением температуры вдоль радиуса, особенно на начальных моментах времени. К концу торможения максимум на графике температуры 3 уже не приходится на один из максимумов графика мощности 4, а находится между ними. Это происходит потому, что по истечении времени кинематическая составляющая уменьшается вследствие торможения, что приводит к меньшей зависимости температуры от поступающей тепловой мощности и большей зависимости от процесса теплопроводности внутри объёма и от граничных условий теплоотдачи.

Температура в окружном направлении из-за неосесимметричности венца несколько выше в области посадки втулок, чем в точках на том же радиусе между соседними такими областями, где теплопередача осуществляется через металл венца. На более удалённых радиусах температуры в окружном направлении практически одинаковы.

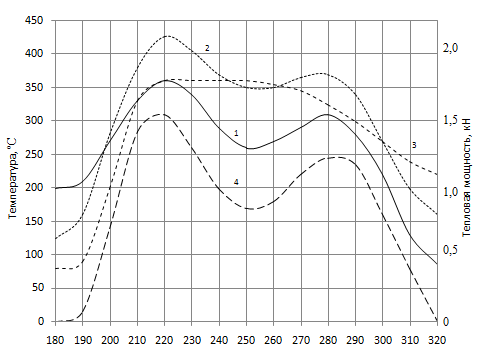
Рис. 3 - Распределение вдоль радиуса венца температуры для моментов времени: 1 – 20 с; 2 – 43 с; 3 – 80 с; 4 – силовая составляющая приведенной тепловой мощности

 

Для исследования изменения температуры в накладке и венце во времени выберем узлы, где температуры достигают максимальных значений, а также узел с максимальными напряжениями растяжения. Соответствующие кривые показаны на рис. 4. Следует отметить наличие максимумов внутри временного интервала для узлов, лежащих на поверхности трения, что также связано с падающим во времени значением тепловой мощности. Превышение в узлах мощности теплоотдачи над подводимой мощностью приводит к падению температуры в этих узлах.

Достижение максимума температуры для накладок раньше, чем для венца, и следующий за ним более интенсивно падающий участок можно объяснить значительно большим значением коэффициента температуропроводности для накладок, чем для венца (рис. 1).

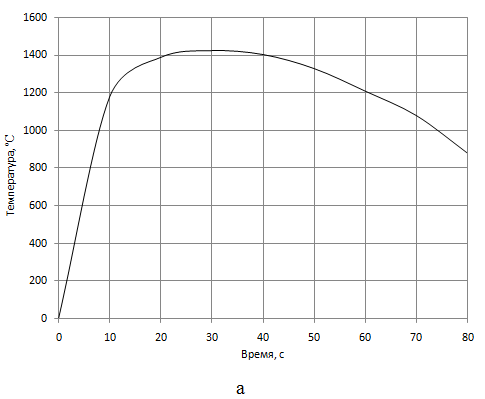
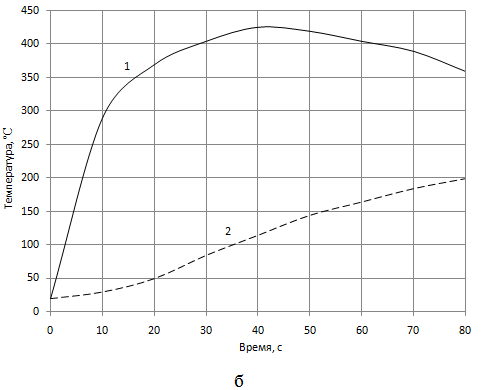
Рис. 4 - Зависимости изменения во времени температуры в узлах с её максимальными значениями для накладок (а) и венца (б) для узлов: 1 – на поверхности трения; 2 – на посадочной поверхности под втулки

 

Изменение температуры в узле с максимальным напряжением растяжения (кривая 2, рис. 4, б) связано с конечностью скорости распространения теплоты, что отражается на задержке во времени наращивания температуры в начальные моменты времени и сдвиге момента достижения максимума, реализации его в конце временного интервала, своего рода тепловая инерция. Распределение температур по толщине венца вдоль линии, содержащей узел с максимальным значением температуры, для моментов времени 20, 43 и 80 с показано на рис. 5. Более равномерное распределение температуры, которое наблюдается в конце временного интервала (кривая 3, рис. 5) несмотря на высокую абсолютную величину, влечёт за собой значительно более низкий уровень напряжений в области сжатия.

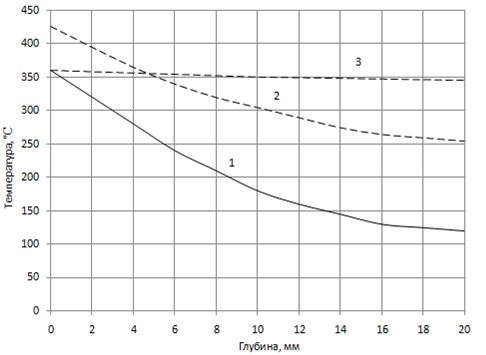
Рис. 5 - Распределение для венца температур на поверхности трения по глубине в моменты времени: 1 – 20 с; 2 – 43 с; 3 – 80 с

 

На рис. 3 и 5 видно, что к концу торможения уровень температур на поверхности трения остаётся достаточно высоким. В зоне посадки под втулки температуры по толщине хоть и выравниваются, но уровень их довольно высок. Все это связано с равномерностью прогрева венца по глубине в конце интервала времени торможения.

Для конечно-элементной модели со слабым отклонением от осевой симметрии при достаточной для вступления в силу граничных условий длительности подвода тепловой мощности получено поле температур практически близкое к осесимметричному (рис. 1), что удовлетворяет условию дальнейшего равномерного подвода теплоты в окружном направлении и доказывает правомерность использования схемы осесимметричного теплового нагружения в такой схеме. При таком подходе используется крупный шаг при интегрировании и соответствующая ему сравнительно большая ширина конечных элементов в окружном направлении, что значительно сокращает размерность конечно-элементной схемы и, соответственно, время расчёта.

Литература

1. Байбакова Е.Н. Тепловое состояние дискового тормоза высокоскоростного подвижного состава: автореф. дис. …канд. техн. наук. – Л.: ЛИИЖТ, 1986. – 22 с.
2. Сакало В.И., Коссов В.С. Контактные задачи железнодорожного транспорта. – М.: Машиностроение, 2004. – 496 с.
3. Берри Г., Барбер Д. Распределение тепла, выделяемого при трении, - путь к изучению природы контактных явлений при скольжении // Труды американского общества инженеров-механиков. Серия «Проблемы трения и смазки». – 1984. – №3. – С. 83-96.
4. Вигак В.М. Оптимальное управление нестационарными тепловыми режимами. – К.: Наукова думка, 1979. – 359 с.
5. Вуколов Л.А. Сравнительные характеристики железнодорожных колодок различных поставщиков / Л.А. Вуколов, В.А. Жаров // Вестник ВНИИЖТ. – №2. – 2005. – С. 16-20.

References

1. Bajbakova E.N. Teplovoe sostojanie diskovogo tormoza vysokoskorostnogo podvizhnogo sostava: avtoref. dis. …kand. tehn. nauk. – L.: LIIZhT, 1986. – 22 s.
2. Sakalo V.I., Kossov V.S. Kontaktnye zadachi zheleznodorozhnogo transporta. – M.: Mashinostroenie, 2004. – 496 s.
3. Berri G., Barber D. Raspredelenie tepla, vydeljaemogo pri trenii, - put' k izucheniju prirody kontaktnyh javlenij pri skol'zhenii // Trudy amerikanskogo obshhestva inzhenerov-mehanikov. Serija «Problemy trenija i smazki». – 1984. – №3. – S. 83-96.
4. Vigak V.M. Optimal'noe upravlenie nestacionarnymi teplovymi rezhimami. – K.: Naukova dumka, 1979. – 359 s.
5. Vukolov L.A. Sravnitel'nye harakteristiki zheleznodorozhnyh kolodok razlichnyh postavshhikov / L.A. Vukolov, V.A. Zharov // Vestnik VNIIZhT. – №2. – 2005. – S. 16-20.