BUILDING OF OPTIMAL STRUCTURE OF THE SYSTEM WITH ACCOUNT TO ITS FUNCTIONAL EFFICIENCY

Алексеев А.П.¹, Абрамов Г.В.², Булгакова И.Н.³

¹Аспирант, ²Доктор технических наук, Профессор, ³Кандидат экономических наук, Воронежский Государственный Университет

ФОРМИРОВАНИЕ ОПТИМАЛЬНОЙ СТРУКТУРЫ СИСТЕМЫ С УЧЕТОМ ЕЕ ФУНКЦИОНАЛЬНОЙ ЭФФЕКТИВНОСТИ

Аннотация

Одним из важнейших вопросов при построении интегрированной системы является определение количественного и качественного состава элементов и взаимосвязей между ними, формирование структуры системы таким образом, чтобы ее эффективность была максимальной.

Особое влияние интегрированные структуры и системы приобрели в сфере мировой экономики, где промышленные и финансовые концерны и кластеры начинают вытеснять отдельные субъекты хозяйствования.

В статье рассматривается задача формирования оптимальной структуры кластера из нескольких предприятий путем сопоставления наиболее успешных партнеров и выполняемых ими функций. При этом менее успешные партнеры исключаются из кластера, а результативность ключевых функций объединения максимизируется.

Предлагается механизм сведения вопроса формирования структуры к задаче о назначениях с использованием оценок типа трудность достижения цели в качестве параметров. Рассмотрен пример использования методики для мясоперерабатывающего кластера в Воронежской области.

Ключевые слова: формирование структуры системы, интеграция предприятий, задача о назначениях, синергетический эффект, трудность достижения цели.

Alekseev A.P.¹, Abramov G.V.², Bulgakova I.N.³

¹Postgraduate student, ²PhD in Engineering, Professor, ³PhD in Economics, Voronezh State University

BUILDING OF OPTIMAL STRUCTURE OF THE SYSTEM WITH ACCOUNT TO ITS FUNCTIONAL EFFICIENCY

Abstract

One of the most important issues by the formation of the integrated system is determination of the quantitative and qualitative composition of elements and the relationships between them, the building of structure of the system so that its efficiency is maximized.

The integrated structures and systems have gained special influence in the world economy because the industrial and financial concerns and clusters begin to displace the individual business entities.

The article considers the task of building of the optimal structure of a cluster of several companies by matching the most successful partners and the functions, performed by them. The less successful partners are excluded from the cluster, and the effectiveness of the key functions of association is maximized.

We propose the mechanism for leading of the task of the structure building to the assignment problem using evaluation of the difficulty of achieving goals as parameters. There is an example of the applying of this technique for meat-processing cluster in the Voronezh region.

Keywords: building of structure of the system, enterprises integration, assignment problem, synergic effect, difficult of achieving the goal.

Развитие мировой экономики сегодня определяют не отдельные субъекты хозяйствования, а интегрированные структуры бизнеса: промышленные концерны, финансово-промышленные группы и кластеры. В научной литературе исследование проблемы формирования и функционирования кластеров связаны с доказанной экономической эффективностью кластеров в мире, а также их положительным влиянием, как на развитие экономики отдельных регионов, так и экономики страны в целом. Экономическая эффективность функционирования кластеров зависит от совокупности взаимосвязанных субъективных и объективных факторов, среди которых важное место занимает проблема формирования оптимальной структуры объединения [1].

Сущность экономического эффекта, возникающего в кластере, основана на синергетическом эффекте. Как отмечают некоторые авторы, синергетический эффект – это эффект взаимодействий, т.е. добавленная стоимость, возникающая в системе, причина которой являются увеличение количества взаимосвязей между участниками этой системы [2].

Формирование кластеров в конкретном регионе зависит, в первую очередь, от наличия в нем предприятий и структур, которые готовы к процессу интеграции и видят в этом свое дальнейшее развитие [1]. При этом важен не столько набор субъектов хозяйствования, сколько их сочетание, оптимальный, качественный и количественный состав кластера. Участники кластера, интегрируясь, а в дальнейшем и сотрудничая, имеют не только разные доходы и расходы, различаются также их способности эффективно выполнять ключевые функции объединения, которые могут измеряться как в количественных, так и в качественных показателях. Определяя состав участников интегрированной структуры, необходимо в первую очередь исходить из стратегии развития всего кластера [1].

В рамках объектной стратегии целесообразно оценивать результаты деятельности кластера, учитывая его функциональную эффективность, с целью выявления наиболее успешно достигающих целей предприятий и наименее успешных партнеров.

В данной статье мы предлагаем механизм формирования структуры кластера таким образом, чтобы комбинация предприятий-партнеров с выполняемыми ими функциями показывала максимальную достижимую эффективность. При этом под функцией в данном случае понимается деятельность партнера в рамках единого процесса, связывающего предприятия кластера, и являющегося основной целью объединения.

Пусть в кластере есть несколько предприятий  и каждое предприятие может выполнять одну или несколько функций f_j(R_j), где , R_j – множество ресурсов, используемых предприятием для выполнения функции, r_jk - k-ресурс для функции . Тогда f_ij(R_j) - j-ая функция i-ого предприятия, для выполнения которой используется множество ресурсов R_j.

Результативность выполнения функции f_ij(R_j) раз­ными предприятиями различна, поэтому обозначим как V_ij результат выполнения j-ой функции i-ым предприятием. Учтем, что результативность выполнения функции имеет гипотетические верхнюю и нижнюю границу, также зависящие от конкретного предприятия: - максимальное возможное значение функции f_ij(R_j).

 - минимальное возможное значение функции f_ij(R_j).

Таким образом, получаем следующее выражения для функций f_ij(R_j):

Можно построить матрицу результативности выполнения функций предприятиями кластера:

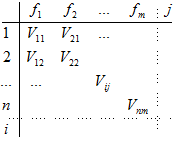
Задача заключается в таком распределении функций f_ij(R_j) между предприятиями, при котором суммарная результативность выполнения всех функций максимальна.

При этом учтем, что в кластере каждая функция должна выполняться хотя бы одним предприятием.

Эта задача может быть сформулирована как задача о назначениях [3]:

Требуется распределить функции f_j(R_j),  между предприятиями . Каждому сочетанию предприятия и функции f_ij(R_j) можно поставить в соответствие параметр c_ij, обозначающий показатель эффективности выполнения функции f_j(R_j) предприятием i, например издержки.

Также сопоставим каждому из возможных вариантов таких сочетаний набор неизвестных , означающих способность i-ого предприятия выполнять j-ую функцию.

Условимся, что:

Каждая функция должна выполняться хотя бы одним предприятием, и каждое предприятие должно выполнять хотя бы одну функцию, поэтому должны выполняться условия [4]:

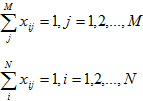
Суммарные издержки выполнения функций предприятиями кластера выражаются суммой [3]:

Таким образом, математическая модель задачи принимает следующий вид [8, 11]:

Результат решения задачи можно выразить в виде матрицы [3]:

Классическая задача о назначениях предполагает минимизацию издержек, однако нам будет удобно изменить задачу так, чтобы целевая функция стремилась к своему максимальному значению, так как наша цель - максимизация результатов выполнения функций предприятиями.

Для задачи о назначениях исходной информацией является матрица  [4], элементами которой служат показатели издержек. Заменим ее на матрицу разниц между максимумом и актуальным значением, для чего заменим каждый элемент исходной матрицы разность этого элемента и максимального значения издержек. Обозначим через  максимальный элемент матрицы. Тогда элементами новой матрицы будут числа [4]:

Теперь обозначим эту разницу как результат выполнения функции:

При этом важно понимать, что результаты выполнения каждой функции могут иметь разные измерения и разную значимость, поэтому гораздо целесообразнее стремиться к минимизации разниц между актуальным значением функции и ее максимумом. Обозначим эту разницу как .

Поскольку возможности по сокращению  ограничены, имеет смысл ввести также гипотетические верхнюю и нижнюю границу, т.е.  .

С учетом сделанных преобразований, мы можем видоизменить матрицу результативности выполнения функций следующим образом:

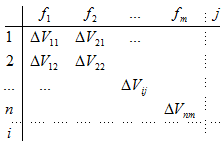
Нужно учесть, что функция может выполняться больше чем одним предприятием, и каждое предприятие должно выполнять хотя бы одну функцию, поэтому должны выполняться условия:

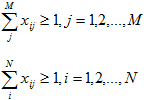
Поскольку наша цель минимизировать разницы  по всему объединению, то задача принимает следующий вид:

Для достижения необходимого эффекта введем понятие трудности достижения минимальной разницы между актуальным значением функции и ее гипотетическим максимумом.

Понятие «трудность» исходит из соображений о том, что получить результат определенного качества тем труднее, чем ниже качество ресурсов, подаваемых на входе, и выше требования к качеству результат на выходе, при прочих равных условиях [5].

Если есть система, на входе которой подается набор ресурсов, необходимых для достижения результата. Величиной μ_i обозначим оценку качества ресурса i, заданную в полуинтервале   [6]. Так как не все значения качества ресурсов достижимы, имеет смысл ввести минимальное требование к качеству ресурса ε_i, так же заданное в полуинтервале  [6]. Невыполнение минимального требования к качеству автоматически ведет к невыполнению требований качества результата, поэтому  [7].

Саму трудность достижения обозначается как  [8].

Для нашей модели оценки такого типа могут применяться для обозначения трудности достижения минимального . Обозначим такие оценки d_ij - трудность достижения наилучшей результативности выполнения функции f_ij(R_j).

Пусть μ_ij - оценка качества выполнения функции. Поскольку наилучший результат достигается при минимальной разнице между актуальной  и минимумом , то нормированное значение оценки качества может быть найдено по формуле:

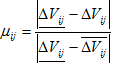
Дополнительно укажем максимальную допустимую разницу между результатами функции и обозначим ее как , причем . Введем оценку удовлетворительного качества выполнения функции:

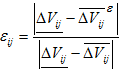
Необходимо отметить, что при такой формулировке . Комбинации, для которых это условие не выполняется, не удовлетворяют минимальным требованиям качества. Показатель трудности в этом случае следует приравнять единице.

Поскольку чем  меньше параметр трудности, тем легче достигнуть оптимального качества, то для нашего случая необходимо изменит формулу этого параметра, поменяв местами числитель и знаменатель. Оценка трудности достижения максимального качества выполнения функции принимает вид:

В этом случае задача сводится к минимизации трудностей для каждой пары предприятие-функция:

Однако стоит иметь в виду, что показатели трудности достижения цели обладают собственными операциями сложения и умножения, а именно [9]:

Чтобы свести оптимизационную функцию к задаче о назначениях, прологарифмируем оценки трудностей и обозначим его параметром C_ij [10, 11]:

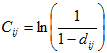
Наша модель сводится к задаче о назначениях со следующими условиями:

Требуется распределить функции f_j(R_j),  между предприятиями . Каждому такому сочетанию поставлен в соответствие параметр - способность i-ого предприятия выполнять j-ую функцию, причем:

Результаты выполнения функции обозначаются как , где   и - максимальное и минимальное значения функции. Разница между этими значениями обозначается как .

Воспользуемся параметрами трудности достижения минимального отклонения:

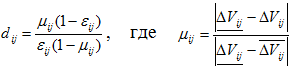 - оценка качества результативности выполнения функции,  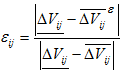- удовлетворительное качество.

Можно построить матрицу результативности выполнения функций предприятиями кластера, следующим образом:

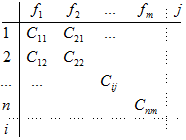
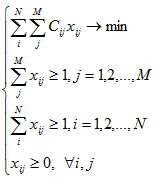Таким образом, задача принимает следующий вид: Учитывая, что _.

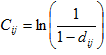Приведем иллюстративный пример по формированию оптимальной структуры кластера из восьми мясоперерабатывающих предприятий Воронежской области, где интенсивно создается производственное объединение для выращивания и переработки мяса крупного рогатого скота. Подобный кластер, повышающий эффективность всех этапов производства, может стать основой для реализации политики импортозамещения.

Одной из целей объединения является повышение конкурентоспособности по четырем направлениям, т.е. каждая из этих функций должна выполняться хотя бы одним из предприятий кластера.

Исходные данные представлены в таблице 1.

Таблица 1 - Функции и предприятия кластера

 

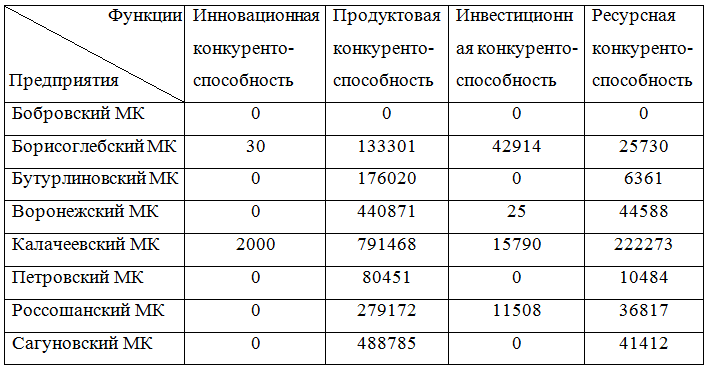
Данные в таблице 1 возьмем как показатели V_ij. В качестве максимального и минимального значений  и используем соответственно максимальное и минимальное значение в каждом столбце.

Тогда таблица значений  будет выглядеть так:

 

Таблица 2 - Отклонения от максимума

 

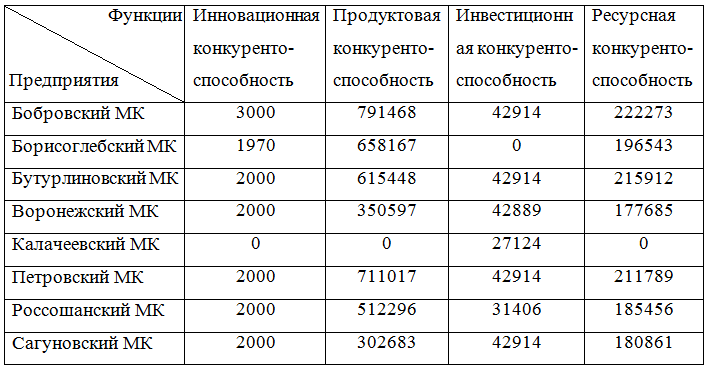
Далее необходимо определить показатели требования и оценки качества:

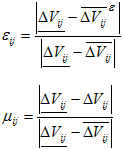
В качестве показателя допустимой разницы  используем следующий вектор для каждого предприятия:

 = (1990, 750000, 30000, 216000)

Тогда вектор требований к качеству для каждого предприятия:

= (0.9950, 0.9476, 0.6990, 0.9718)

Показатели оценки качества представлены в таблице 3.

 

Таблица 3 - Оценки качества результативности функций

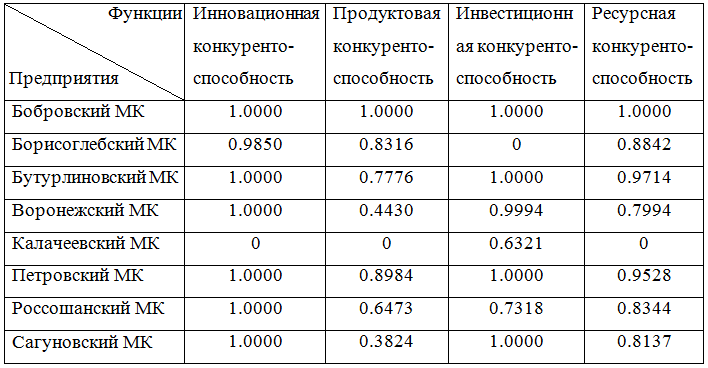
На основании полученных данных вычислим трудности достижения целей для всех комбинаций. , учитывая что при,  .

Полученные данные представлены в таблице 4.

Таблица 4 - Трудности достижения минимального отклонения

Наконец, вычислим показатели .  

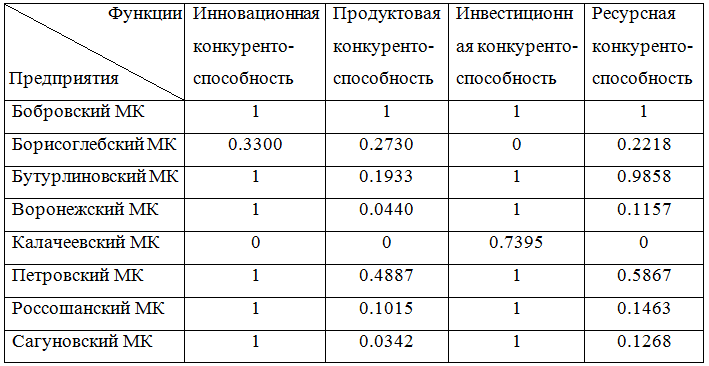
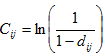Таблица 5 - Логарифмированные трудности

 

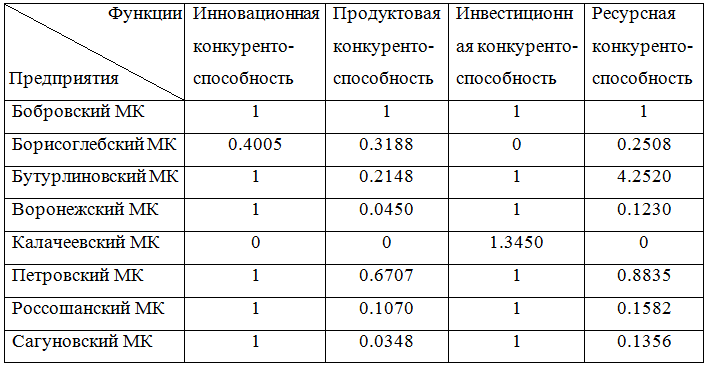
Применим к задаче венгерский алгоритм, используя данные из таблицы 5.

В результате вычислений получаем следующую таблицу соответствия предприятий и функций (показатели ):

Таблица 6 - Оптимальная структура кластера

 

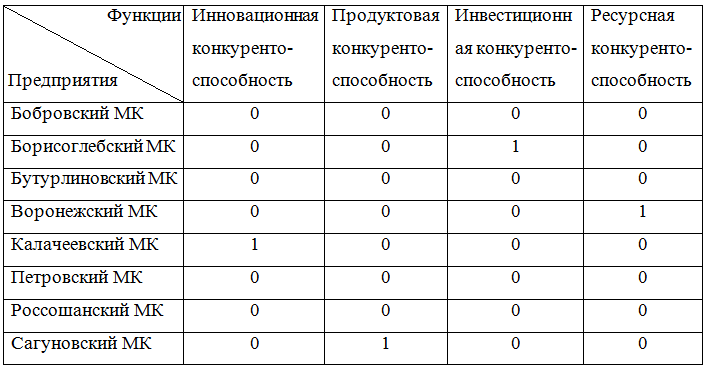
Оптимизационная функция в этом случае равна:  = 0.1578

В итоге, максимальная эффективность выполнения функций повышения конкурентоспособности достигается при создании кластера из мясокомбинатов Борисоглебский, Воронежский, Калачеевский, Сагуновский. Остальные партнерами являются менее успешными и не входят в объединение.

При этом трудность достижения наилучшего качества выполнения всех функций в этом объединении равна целевой функции, т.е. 0.1578.

Для интерпретации полученного результата воспользуемся шкалой желательности, предложенной Э. Харрингтоном [12], при этом учитывая, что чем ниже трудность, тем более она желательна:

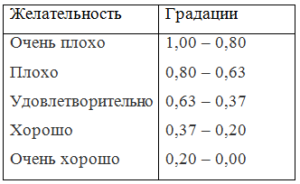
Таким образом, сформированная нами система получает очень хороший результат по показателю трудности достижения максимальной функциональной эффективности.

Литература

1. Буснюк С.В. Формирование оптимальной структуры и системы управления кластером // Проблемы экономики и менеджмента. 2014. № 1 (29). С. 17-22.
2. Несмачных О.В. 1 Литовченко В.В. Структурная стратегия управления кластером // Международный журнал прикладных и фундаментальных исследований. 2014. № 8 (часть 1). С. 148-151.
3. Афанасьев М.Ю., Б.П. Суворов. Исследование операций в экономике: модели, задачи, решения // Учеб. пособие. М.: ИНФРА-М, 2003. 444 с. (Серия «Высшее образование»).
4. Зандер Е. В. Исследование операций в экономике: учеб. пособие / Е. В. Зандер, В. П. Злодеев, Л. И. Мошкович, А. Р. Семёнова. Сибирский федеральный ун-т. Красноярск. 2007. 202 с.
5. Булгакова И.Н., Саликов Ю.А. Совершенствование модели развития социально-экономических систем // Современная экономика: проблемы и решения – Воронеж, 2010 - №2(2) – С. 146-154.
6. Алексеев А.П. Использование модели Р. Стоуна для оценки синергетического эффекта процесса интеграции предприятий // Наука и образование в жизни современного общества. 2014. №11. С. 10-11.
7. Алексеев А.П. Использование трудности достижения цели для оценки синергетического эффекта при создании интегрированных структур / А.П. Алексеев, Г.В. Абрамов, И.Н. Булгакова // Международный научно-исследовательский журнал. 2015. №10-2 (41). С.6-10.
8. Руссман И.Б. Интегральные оценки качества в организационных системах // Сборник "Структурная адаптация сложных систем управления", Изд. ВПИ, Воронеж, 1977, с. 90-92.
9. Бермант М.А., Руссман И.Б. О проблеме оценки качества // Экономика и математические методы. 1978. №4.
10. Булгакова И.Н. Модель оптимального размещения интегрированных структур агропромышленного комплекса // Международный научно-исследовательский журнал. 2015. №7-3 (38). С.17-19.
11. Каплинский А. И., Руссман И.Б., Умывакин В.М. Моделирование и алгоритмизация слабо-формализованных задач выбора наилучших вариантов системы . Воронеж: Изд-во ВГУ, 1991. 168 с.
12. И. Н. Булгакова, А. Н. Морозов. Использование «функции желательности» для формализации комплексного показателя конкурентоспособности промышленного предприятия // Вестник ВГУ. Серия: экономика и управление. 2009. № 2. С. 54-56.

References

1. Busnjuk S.V. Formirovanie optimal'noj struktury i sistemy upravlenija klasterom // Problemy jekonomiki i menedzhmenta. 2014. № 1 (29). S. 17-22.
2. Nesmachnyh O.V. 1 Litovchenko V.V. Strukturnaja strategija upravlenija klasterom // Mezhdunarodnyj zhurnal prikladnyh i fundamental'nyh issledovanij. 2014. № 8 (chast' 1). S. 148-151.
3. Afanas'ev M.Ju., B.P. Suvorov. Issledovanie operacij v jekonomike: modeli, zadachi, reshenija // Ucheb. posobie. M.: INFRA-M, 2003. 444 s. (Serija «Vysshee obrazovanie»).
4. Zander E. V. Issledovanie operacij v jekonomike: ucheb. posobie / E. V. Zander, V. P. Zlodeev, L. I. Moshkovich, A. R. Semjonova. Sibirskij federal'nyj un-t. Krasnojarsk. 2007. 202 s.
5. Bulgakova I.N., Salikov Ju.A. Sovershenstvovanie modeli razvitija social'no-jekonomicheskih sistem // Sovremennaja jekonomika: problemy i reshenija – Voronezh, 2010 - №2(2) – S. 146-154.
6. Alekseev A.P. Ispol'zovanie modeli R. Stouna dlja ocenki sinergeticheskogo jeffekta processa integracii predprijatij // Nauka i obrazovanie v zhizni sovremennogo obshhestva. 2014. №11. S. 10-11.
7. Alekseev A.P. Ispol'zovanie trudnosti dostizhenija celi dlja ocenki sinergeticheskogo jeffekta pri sozdanii integrirovannyh struktur / A.P. Alekseev, G.V. Abramov, I.N. Bulgakova // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. 2015. №10-2 (41). S.6-10.
8. Russman I.B. Integral'nye ocenki kachestva v organizacionnyh sistemah // Sbornik "Strukturnaja adaptacija slozhnyh sistem upravlenija", Izd. VPI, Voronezh, 1977, s. 90-92.
9. Bermant M.A., Russman I.B. O probleme ocenki kachestva // Jekonomika i matematicheskie metody. 1978. №4.
10. Bulgakova I.N. Model' optimal'nogo razmeshhenija integrirovannyh struktur agropromyshlennogo kompleksa // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. 2015. №7-3 (38). S.17-19.
11. Kaplinskij A. I., Russman I.B., Umyvakin V.M. Modelirovanie i algoritmizacija slabo-formalizovannyh zadach vybora nailuchshih variantov sistemy . Voronezh: Izd-vo VGU, 1991. 168 s.
12. I. N. Bulgakova, A. N. Morozov. Ispol'zovanie «funkcii zhelatel'nosti» dlja formalizacii kompleksnogo pokazatelja konkurentosposobnosti promyshlennogo predprijatija // Vestnik VGU. Serija: jekonomika i upravlenie. 2009. № 2. S. 54-56.