DYNAMIC IMITATION MODELING OF INDUCTION MACHINE USING EQUATIONS FOR INSTANTENEOUS ELECTROMAGNETIC VALUES

Петров А.В.¹, Котельников А.П.², Плохов И.В.³

¹ORCID: 0000-0002-2230-342X, Аспирант, ²ORCID: 0000-0002-0769-8980, Соискатель, ³ORCID: 0000-0002-9953-7216, Доктор технических наук, профессор, Псковский государственный университет

ДИНАМИЧЕСКОЕ ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ АСИНХРОННОЙ ЭЛЕКТРИЧЕСКОЙ МАШИНЫ С ИСПОЛЬЗОВАНИЕМ ВЫРАЖЕНИЙ ДЛЯ МГНОВЕННЫХ ЗНАЧЕНИЙ ВЕЛИЧИН

Аннотация

В статье представлены результаты разработки и реализации в среде MATLAB динамической имитационной модели асинхронной электрической машины, предназначенной для повышения эффективности проектирования и изготовления асинхронных электродвигателей, построенной на основе выражений для мгновенных значений электромагнитных величин. В модели учтены конструкционные параметры обмоток статора и ротора, а также геометрические размеры машины. Приведены результаты вычислительного эксперимента.

Ключевые слова: математическая модель, динамическое моделирование, асинхронная машина, переходные процессы.

Petrov A.V.¹, Kotelnikov A.P.², Plokhov I.V.³

¹ORCID: 0000-0002-2230-342X, Postgraduate student, ²ORCID: 0000-0002-0769-8980, Postgraduate student, ³ORCID: 0000-0002-9953-7216, PhD in Engineering, professor, Pskov State University

DYNAMIC IMITATION MODELING OF INDUCTION MACHINE USING EQUATIONS FOR INSTANTENEOUS ELECTROMAGNETIC VALUES

Abstract

This paper gives the results of development and implementation of dynamic simulation model of induction machine designed with equations for instantaneous electromagnetic values in the programming environment MATLAB. The goal of development of the model is the improvement of designing and manufacturing of induction motors. Considered are construction parameters of stator and rotor windings, as well as geometric dimensions of the machine. The results of the computing modelling are given.

Keywords: mathematical model, dynamic modelling, induction machine, transient processes.

Асинхронные машины сегодня составляют большую часть электрических машин, и нашли широкое применение в различных отраслях промышленности и сельского хозяйства.

При выборе существующих типовых и проектировании модифицированных асинхронных электродвигателей, а также проектировании новых серий асинхронных машин возникает необходимость в получении и оценке динамических характеристик, а также в оптимизации их параметров по избранным критериям.

На сегодняшний день существует несколько программных пакетов, способных рассчитывать статические характеристики асинхронных машин, а также проводить оптимизацию статических параметров. Однако такие программные пакеты не дают возможности:

1. расчета динамических характеристик асинхронной машины с учетом ее основных конструкционных параметров;
2. проведения автоматизированной оптимизации параметров машины, а также оптимизации по критериям наилучшей динамики и качества переходных процессов.

Общие темпы производства асинхронных машин постоянно нарастают, а также увеличивается потребность в асинхронных машинах специальных исполнений, выпускаемых малыми сериями. Поэтому учет влияния конструкционных параметров машин на их динамические характеристики с возможностью оптимизации этих параметров позволит повысить эффективность и оперативность их проектирования и изготовления. Следовательно, разработка математической модели (с возможностью создания на ее основе программы инженерного расчета и проектирования асинхронной электрической машины) является актуальной [1, 2].

Общие задачи исследования:

1. имитационное моделирование работы асинхронной машины с учетом большинства ее основных параметров;
2. верификация модели путем расчета статических и динамических характеристик машины, и сравнения их с паспортными характеристиками;
3. получение кривых переходных процессов всех электромагнитных и механических величин;
4. формирование подходов к разработке критериев оптимизации асинхронной электрической машины.

В данной статье представлен этап исследования, связанный с преобразованием математической модели, построенной на основе классической теории электрических машин, с целью достижения возможности моделирования колебательного характера переходных процессов, а также наблюдения пиковых значений токов и электромагнитного момента, развиваемого машиной.

Исходная математическая модель

Для имитационного моделирования работы асинхронной машины с учетом широкого спектра ее конструкционных параметров, а также получения кривых переходных процессов всех электромагнитных величин на первом этапе работы была выбрана известная математическая модель асинхронного двигателя с роторной обмоткой, приведенной к статорной, а также рабочим режимом, приведенным к режиму с заторможенным ротором.

Кроме того, были приняты следующие допущения:

1) потери в сердечниках статора и ротора отсутствуют;

2) механические и добавочные потери в машине отсутствуют.

Электрическая схема замещения двигателя с указанными допущениями представлена на рис 1.

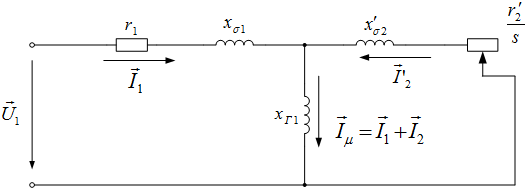
Рис. 1 – Электрическая схема замещения асинхронной машины

 

На данной схеме:  – векторное значение фазного напряжения обмотки статора;  – векторные значения тока фазы обмотки статора и приведенного тока фазы обмотки ротора;  – ток намагничивания;  – активное сопротивление фазы обмотки статора и приведенное активное сопротивление фазы обмотки ротора;  – индуктивное сопротивление рассеяния фазы обмотки статора и приведенное индуктивное сопротивление рассеяния фазы обмотки ротора;  – индуктивное сопротивление главных полюсов;  – величина скольжения асинхронной машины.

Уравнения баланса напряжений такого двигателя:

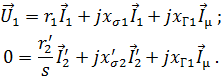
Величина  представляет собой вектор ЭДС индукции, создаваемый основной гармоникой магнитного потока в обмотках [3, 6]:

Преобразование уравнений баланса напряжений

Недостатком приведенной модели является то, что она не отражает колебательный характер переходных процессов в электрической машине, а также не позволяет получить информацию о величинах пиковых значений токов и момента при пуске. Обойти указанный недостаток можно перейдя от векторных (комплексных) значений к мгновенным.

При переходе от векторных значений к мгновенным, с учётом принятых ранее допущений:

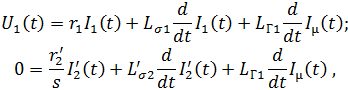
где  – индуктивность рассеяния фазы обмотки статора;  – приведенная индуктивность рассеяния фазы обмотки ротора;  – главное индуктивное сопротивление обмотки статора.

В полученных выражениях присутствует операция дифференцирования. Математическая модель будет реализовываться в среде имитационного моделирования, в которой возможно внесение погрешностей в расчёт дифференцирующими звеньями. Чтобы устранить данный недостаток, производим замену операции дифференцирования на операцию интегрирования:

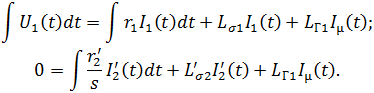
Учет параметров, отражающих конструктивные особенности элементов машины

Индуктивные сопротивления рассеяния статорной и роторной обмоток рассчитываются согласно соотношениям:

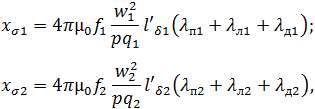
где μ₀ – магнитная постоянная; p – число пар полюсов машины; q₁,q₂ – числа пазов статора на полюс и фазу; w₁,w₂ – числа витков в одной фазе обмоток статора и ротора;  – расчетные длины полей рассеяния статора и ротора (зависят от величины радиальных вентиляционных каналов в сердечниках);  – коэффициенты магнитной проводимости пазового рассеяния обмоток статора и ротора (зависят от конфигурации и геометрических размеров пазов);  – коэффициенты магнитной проводимости рассеяния лобовых частей обмоток (зависят от типа обмоток, величины их лобовых частей и укорочения шага обмоток);  – коэффициенты магнитной проводимости дифференциального рассеяния (зависят от размерных соотношений зубцовых зон и воздушного зазора); все коэффициенты магнитной проводимости рассчитываются по формулам, приведенным в [5] (стр. 199–204).

С учётом того, что:

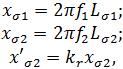
где k_r – коэффициент приведения сопротивлений, зависящий от числа фаз обмоток статора и ротора, числа витков в каждой фазе обмоток и обмоточных коэффициентов статора и ротора, индуктивности рассеяния статорной и проведенной роторной обмоток определяются:

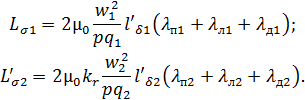
Активное сопротивление фазы статорной обмотки, и, с учётом того, что , приведенное активное сопротивление фазы обмотки фазного ротора рассчитываются как:

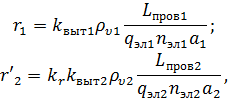
где  – коэффициенты увеличения активных сопротивлений фазы статора и ротора под действием эффекта вытеснения тока;  – удельное сопротивление материалов обмоток при расчетной температуре;  – общая длина эффективных проводников фазы обмоток;  – сечение элементарных проводников в обмотках;  – числа элементарных проводников в одном эффективном в обмотках статора и ротора;  – числа параллельных ветвей обмоток.

Приведенное активное сопротивление фазы короткозамкнутого ротора определяется следующим образом:

где  – удельные сопротивления материалов стержней и короткозамыкающих колец при расчетной температуре;  – сечения стержней и к.з. колец; l_c – длина одного стержня;   – средний диаметр к.з. колец; Z₂ – число стержней ротора;  – коэффициент увеличения сопротивления стержня под действием эффекта вытеснения тока; Δ – коэффициент приведения токов в кольце к току в стержне [5].

Величина потокосцепления машины  может быть найдена как (соотношение выведено на основании выражений 1.111 в [1], а также 23-10 в [3]):

где  τ – полюсное деление;  – расчетная длина сердечника статора;  – коэффициент насыщения магнитной цепи машины (является динамическим и зависит от соотношения долей МДС ярм, зубцов и воздушного зазора машины);  – коэффициент воздушного зазора (зависит от размерных соотношений зубцовых зон и воздушного зазора); δ – величина одностороннего воздушного зазора;  – обмоточный коэффициент статорной обмотки.

Расчет магнитной цепи

Выражение для потокосцепления машины является результатом нескольких последовательных преобразований.

Мгновенное значение результирующей МДС, создаваемой обмотками машины:

МДС воздушного зазора рассчитывается по выражению: Коэффициент насыщения магнитной цепи:

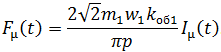
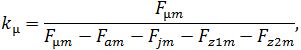
где  – амплитудное значение результирующей МДС магнитной цепи машины;  – амплитудные значения долей МДС, приходящихся на ярма статора и ротора;  – амплитудные значения долей МДС, приходящихся на зубцы статора и ротора.

Индукция в воздушном зазоре машины определяется как: Магнитный поток машины выражается следующим образом:

Потокосцепление рассчитывается по соотношению (выведенному на основании выражения 24-6 в [3]) [1, 3 ,5]:

Расчет механической цепи машины

Развиваемый машиной электромагнитный момент может быть определен согласно выражению [3]:

Уравнение движения: где   – амплитудное значение развиваемого электромагнитного момента;  – момент нагрузки на валу машины;  – совокупный момент инерции, приведенный к валу машины;  Ω – угловая скорость вращения вала. Величина скольжения асинхронной машины рассчитывается как [4]:

Реализация в среде имитационного моделирования

Математическая модель асинхронной машины реализована в среде MATLAB Simulink. Исходными данными к моделированию являются конструкционные и обмоточные данные выбранного асинхронного двигателя MF13X-200-192F.

После построения имитационной модели в пакете MATLAB Simulink было произведено моделирование пуска асинхронного электродвигателя при номинальных параметрах.

Параметры эксперимента:

f₁ = 50 Гц – номинальная частота напряжения питающей сети;

U₁  = 192.26 В – номинальное фазное напряжение обмотки статора при частоте питающего напряжения 50 Гц;

M_нагр – номинальный статический момент нагрузки.

t_вкл – время включения двигателя под напряжение.

Временные зависимости некоторых величин, полученные в ходе проведения эксперимента, представлены на рис. 2 (величины на рисунке приведены в относительных единицах – в отношении к номинальным паспортным данным).

 

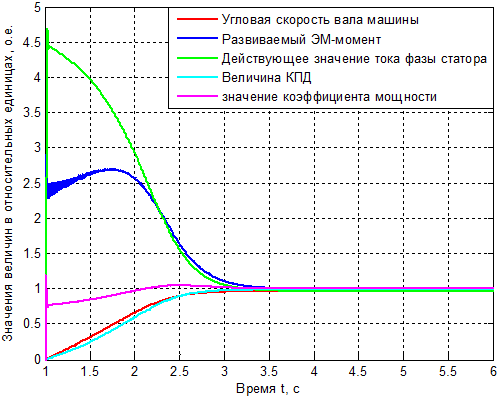
Рис. 2 – Временные пусковые диаграммы

 

Установившиеся значения динамических характеристик, полученные в результате имитационного моделирования, совпадают с паспортными с достаточной точностью.

На рис. 3 представлены временные диаграммы изменения действующих значений тока статора и приведенного тока фазы ротора при пуске.

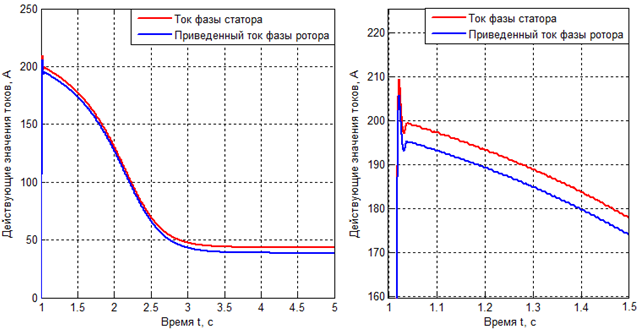
Рис. 3 – временные диаграммы действующих значений фазных токов при пуске

 

Начальная точка по оси абсцисс на диаграммах соответствует моменту включения моделируемой асинхронной машины в сеть.

На рис. 4 представлена временная диаграмма изменения величины развиваемого машиной электромагнитного момента при пуске.

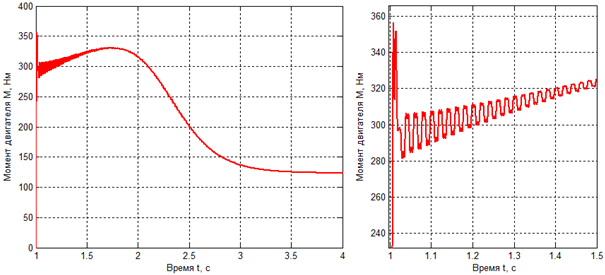
Рис. 4 – Временная диаграмма изменения развиваемого электромагнитного момента машины при пуске

 

На рис. 5 представлена механическая характеристика моделируемой машины при пуске.

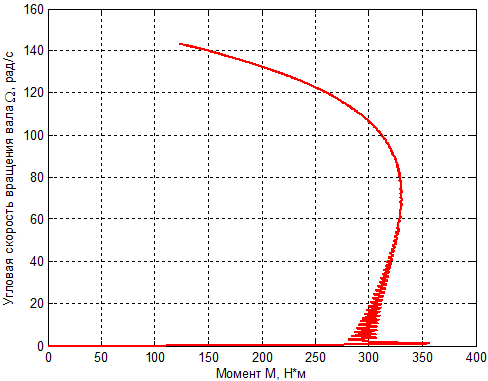
Рис. 5 – Механическая характеристика моделируемой машины при пуске

Выводы При использовании в динамической имитационной модели выражений для мгновенных значений величин удалось добиться возможности моделирования колебательного характера переходных процессов, а также наблюдать пиковые значения токов и развиваемого электромагнитного момента асинхронной машины. Полученная модель с достаточной точностью описывает поведение электрической машины в процессе ее работы. Вид полученных характеристик совпадает с видом теоретических. Практическая ценность моделирования колебательного характера переходных процессов в асинхронной машине заключается в том, что при этом достигается возможность выбрать в качестве одного из критериев оптимизации степень устойчивости работы асинхронной машины. Это является особенно важным для машин, работающих в реверсивном и повторно-кратковременном режиме. Следующим этапом работы станет дальнейшее усовершенствование модифицированной динамической имитационной модели путем учета магнитных, механических и добавочных потерь, учета влияния эффектов насыщения и вытеснения тока на характеристики машины, а также экспериментальная верификация модели с использованием разработанного испытательного стенда.

Литература

1. Копылов И.П. Электрические машины: учеб. для вузов / И.П. Копылов. – 3-е изд., испр. – М.: Высш. шк., 2002. – С. 42-223.
2. Моделирование и прогнозирование в системном проектировании: Учебное пособие / А.Л. Куранов, С.Н. Обрядин, И.В. Плохов, А.А. Салангин. – Псков: Издательство ПсковГУ, 2012. – 292 с.
3. Вольдек А.И. Электрические машины: учебник для студентов высших технических учебных заведений / А.И. Вольдек – 3-е изд., перераб. – Л.: Энергия, 1978. – С. 385-523.
4. Вешеневский С.Н. Характеристики двигателей в электроприводе / С.Н. Вешеневский. – 6-е изд., испр. – М.: Энергия, 1977. – 432 с.
5. Проектирование электрических машин: учебное пособие для вузов / под ред. И.П. Копылова. – М.: Энергия, 1980. – 496 с.
6. Петров А.В. Динамическое моделирование асинхронной электрической машины с учетом конструкционных параметров / А.В. Петров, А.П. Котельников, И.В. Плохов // Научно-технический вестник Поволжья. – – №1. – С. 121-126.

References

1. Kopylov I.P. Jelektricheskie mashiny: ucheb. dlja vuzov / I.P. Kopylov. – 3-e izd., ispr. – M.: Vyssh. shk., 2002. – S. 42-223.
2. Modelirovanie i prognozirovanie v sistemnom proektirovanii: Uchebnoe posobie / A.L. Kuranov, S.N. Obrjadin, I.V. Plohov, A.A. Salangin. – Pskov: Izdatel'stvo PskovGU, 2012. – 292 s.
3. Vol'dek A.I. Jelektricheskie mashiny: uchebnik dlja studentov vysshih tehnicheskih uchebnyh zavedenij / A.I. Vol'dek – 3-e izd., pererab. – L.: Jenergija, 1978. – S. 385-523.
4. Veshenevskij S.N. Harakteristiki dvigatelej v jelektroprivode / S.N. Veshenevskij. – 6-e izd., ispr. – M.: Jenergija, 1977. – 432 s.
5. Proektirovanie jelektricheskih mashin: uchebnoe posobie dlja vuzov / pod red. I.P. Kopylova. – M.: Jenergija, 1980. – 496 s.
6. Petrov A.V. Dinamicheskoe modelirovanie asinhronnoj jelektricheskoj mashiny s uchetom konstrukcionnyh parametrov / A.V. Petrov, A.P. Kotel'nikov, I.V. Plohov // Nauchno-tehnicheskij vestnik Povolzh'ja. – 2015. – №1. – S. 121-126.