DYNAMICS OF ECONOMIC PROCESSES IN ENTERPRISES BASED ON THE EXAMPLE OF THE MODEL SYSTEM OF PMR

Для описания экономических процессов предприятий часто используются методы математического моделирования

Рассматриваемая модель ПУР (производство, управление, ресурс) относится к динамическим моделям предприятий. Наряду с достаточной простотой она учитывает основные факторы производств: динамику производства, управление и баланс внешнего и производимого в системе ресурса.

Модель представляет собой три балансных, нелинейных, дифференциальных уравнения соответствующая трем составляющим искомый экономический объект подсистемам — производству, управлению и ресурсу.

Для анализа динамики системы, оценки стабильности и возможных неустойчивостей используются методы и критерии данные авторами в работе

Уравнения модели ПУР в безразмерном виде равны

Здесь  

В первом уравнении системы (1), описывающем динамику производства слагаемые ax, bxz соответствуют прибыли в результате производства и вводимого ресурса; слагаемое  xy — убыль на управление (например, на обучение, повышение квалификации, и т.д.) Во втором уравнении для управления yx, dyz приход средств от производства и вводимого ресурса; cy — непосредственные расходы на управление.

Третье уравнение — баланс внутреннего и внешнего r ресурса (r > 0 — кредитование, r < 0 — погашение долгов). Слагаемые hx, ky — непосредственная убыль ресурса на зарплаты в производстве и управлении; ez — затраты ресурса на погашение процентов при кредитовании или получение процентов по вкладам, bxz — затраты ресурса на сырье для производства, энергию и т.д. Слагаемые gxy, dyz соответственно — прибыль ресурса за счет производства и убыль на инновации в управлении и автоматизации производства.

Далее в

решениями системы уравнений (2). В данном случае, существует пять стационарных решений соответственно равных

Линеаризацией системы (1) относительно стационарных решений получаем систему уравнений для возмущений

где λ — спектральный параметр (собственные значения эволюционной матрицы E, eα,β  элементы эволюционной матрицы равные

Собственные значения эволюционной матрицы, определяемые спектральным уравнением (СУ) (6) имеющем вид

 (I  — единичная матрица) характеризуют динамику системы.

А именно:

1) если все собственные значения – корни СУ имеют отрицательные вещественные части — исследуемое состояние устойчиво относительно малых возмущений;

2) если существует хотя бы один корень с положительной вещественной частью — состояние неустойчиво;

3) если в спектре есть корни с положительной и отрицательной вещественными частями (седловой фокус) и некоторые из них комплексные — то это представляет собой особый вид неустойчивости — хаос (нерегулярные хаотические колебания).

В виду сложности системы (1) возможен только численный анализ спектра, для чего необходимо задать численные значения безразмерных коэффициентов, а также выбрать несколько (один, два) управляющих параметров, варьируя значениями которых наблюдают за изменением спектра и тем самым за динамикой системы. В качестве управляющих параметров выберем параметр внешнего ресурса — r, параметры инновации в управлении и производстве — d, g. Численные значения остальных параметров в системе (1) выбираются в соответствии с реальными величинами на современных производствах и, с учетом предварительного счета, который показывает, что влияние величин (a, b, c, h, k) на динамику системы на так существенно как величин (e, d, g, r) поэтому первые выбраны постоянными (см. табл. 3), а вторые изменяются в диапазонах (7).

Спектральные коэффициенты в (6) принимают вид

Для анализа динамики возмущений используем как непосредственный расчёт корней спектрального уравнения, так и критерии неустойчивости и хаоса данные авторами в работах

Неравенства (а) в (9) являются условиями устойчивости-неустойчивости, (b) — отражает седлообразный характер спектра, реализация всех трех условий отражает наличие в системе хаотических колебаний (хаоса).

Последовательно рассмотрим устойчивость состояний St1,2,3,4,5.

а) Стационарное состояние St1, xs = ys = 0; zs = r/e.

Из (5,6) следует, что для элементов эволюционной матрицы и спектрального уравнения имеем:

Из (11) следует, что в состоянии с неработающим производством и управлением все возмущения ресурсной сферы затухают.

б) Стационарное состояние St2, из (5,6) следует 

Из (12) следует, что при неработающем производстве в зависимости от параметров возмущения управленческой и ресурсной сфер как могут затухать, так и меняются разнонаправленно (т.е. λ2>0, λ3<0 ) в этом случае состояние St2 неустойчиво.

в) Стационарное состояние St3, из (5, 6) следует

Из (13) следует, что при неработающем управлении в зависимости от параметров возмущения производственной и ресурсной сфер как могут затухать (при r=0), так и меняются разнонаправленно (при r≠0 т.е. λ1>0, λ3<0 ) в этом случае состояние неустойчиво.

Наибольший практический интерес представляют стационарные состояния с ненулевыми значениями величин, т.е. St4, St5 для которых соответственно (с учетом (2), (6)) получаем:

Графическим отображением условий неустойчивости (9) является критериальная поверхность – поверхность в пространстве параметров (П) отображающая области устойчивости–неустойчивости S(П)≡K1=q-s⋅p и нейтральные кривые разделяющие области устойчивых состояний от неустойчивых, т.е., каждая точка нейтральной кривой есть отображение в пространстве параметров нуля спектрального уравнения (6). Например, для параметров (a = b = 0,3, h = 0,2, k = 0,4, c = 0,5, e = -0,2, r = 0,1) уравнения критериальной поверхности S(d,g) и нейтральной кривой gcr=f(dcr ) соответственно имеют вид (15, 16).

Графики критериальной поверхности и нейтральной кривой приведены на рисунках 1, 2.

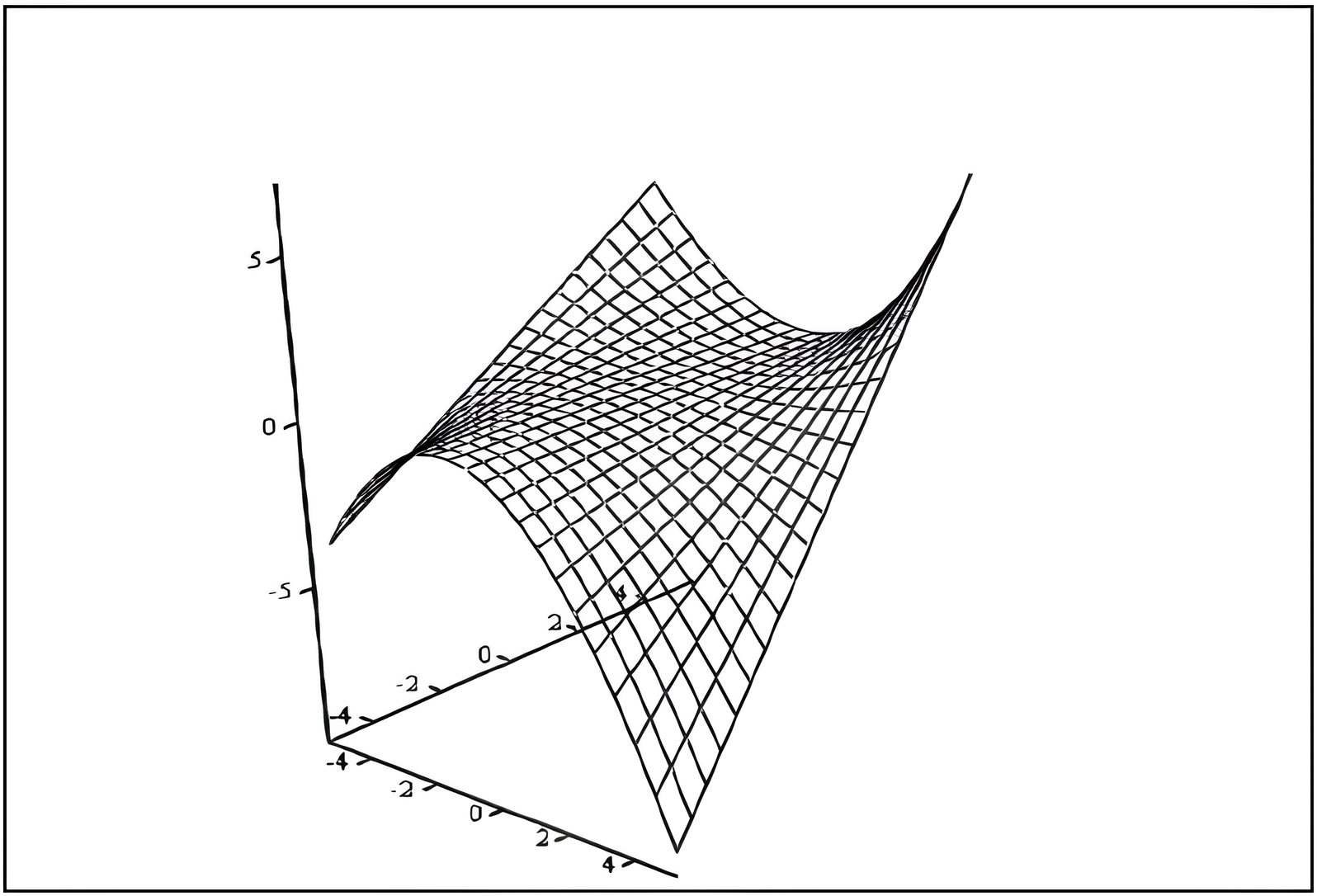
Рисунок 1 - Критериальная поверхность S(d,g) в координатах ОХ – g; OY – d; OZ – S

DOI:10.60797/IRJ.2025.158.103.1

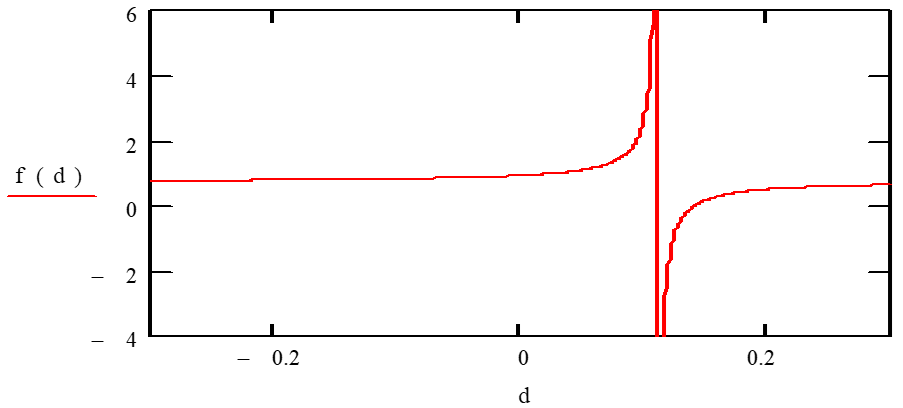
Рисунок 2 - Нейтральная кривая g(cr) в координатах g, d

DOI:10.60797/IRJ.2025.158.103.2

На графике критериальной поверхности, состояния для которых поверхность переходит в отрицательную полуплоскость, становятся устойчивыми, т.е. предприятия функционируют стабильно, напротив, состояния при которых часть поверхности расположена в верхней полуплоскости неустойчивы, предприятие лихорадит. На графике нейтральной кривой устойчивым состояниям соответствуют состояния параметрами d и g лежащими ниже нейтральной кривой. Из (15,16) следует, что пик нейтральной кривой соответствует состоянию, при котором критерий (и соответственно динамика) перестают зависеть от параметра g.

В таблицах 1, 2 приведен непосредственный счет корней спектрального уравнения (6) и критериев (9) для состояния St4 в зависимости от параметров d, g, r.

Cчет корней уравнения (6) для состояния St5 показывает, что для большинства параметров в указанных диапазонах (7) состояние St5 является неустойчивым. Например, расчет корней для параметров e = 0,1, d = 0,1, g = 0,2, r = 0,3, а остальные см. (7) — показывает, что система находится в состоянии сильной неустойчивости m (т.е. λ1 = 0,119, λ2 = 9,2, λ3 = -9,67).

В таблицах также учтено, что спектральное уравнение (6) есть уравнение третьей степени с вещественными коэффициентами и имеет либо три вещественных корня, либо один вещественный и два комплексно-сопряженных, т.е. (λ1, λ2, λ3); (λ1, λ2,3 ± iω).

Из таблицы 1 следует, что увеличение инвестиций в управление и производство (при прочих равных условиях) стабилизирует работу предприятия, напротив уменьшение инвестиций приводит к дестабилизации и хаосу (см. выделенные в таблице режимы). Из таблицы 2 следует, что увеличение кредитования даже при недофинансировании инвестиций также приводит к стабилизации системы.

Из таблицы 3 видно, что характер динамики возмущений не меняется в зависимости от изменения параметров a, b, k, h.

В целом, анализируя результаты вычислений и рисунки можно отметить следующее:

1. Предложенная модель дает широкие возможности для исследования влияния на экономическую деятельность предприятий различных факторов производственной, управленческой и ресурсной сферы.

2. Данная модель описывает весьма динамичную систему, в которой наряду с областями стабильности есть области неустойчивости и хаоса, существенно зависящие от параметров системы.

3. Результаты таблиц 1, 2, 3 подтверждают (в рамках рассмотренной модели) правильность выбора управляющих параметров и несущественное влияние остальных.

4. Из возможных стационарных состояний в данной модели наиболее оптимальным для управления динамикой и обеспечения стабильности функционирования предприятия путем вариации управляющими параметрами является состояние St4.

5. Из таблиц 1, 2 расчета спектров следует, что основными факторами, влияющими на стабильность функционирования предприятий (в рамках данной модели) являются инвестиции в производство и управление.

6. Из таблиц 1, 2 также видно, что даже при недостаточном уровне инвестиций стабильность может быть обеспеченна внешним кредитованием.

7. Критерии неустойчивости и хаоса, предложенные авторами, полностью согласуются с расчетом спектра и могут быть использованы для прогнозирования областей стабильности и неустойчивости динамических систем.