MR IMAGES DENOISING BY MULTILEVEL WAVELET-ANALYSIS

Казначеева А.О.

Кандидат технических наук, доцент, Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики

СНИЖЕНИЕ ЗАШУМЛЕННОСТИ ТОМОГРАММ С ПОМОЩЬЮ МНОГОУРОВНЕВОГО ВЕЙВЛЕТ-АНАЛИЗА

Аннотация

В работе представлен способ обработки магнитно-резонансных (МР) томограмм, позволяющий снизить уровень случайного шума и состоящий в расчете коэффициентов дискретного вейвлет-преобразования непосредственно в фазово-частотном пространстве данных и последующей реконструкции томограммы. Оценка результата выполнялась для четырех типов данных: полученных с однократным накоплением МР-сигнала, реконструированных после вейвлет-анализа k-пространства, вейвлет-фильтрации изображений, томограмм с несколькими усреднениями сигнала. Показано, что вейвлеты снижают шум на 30% для анатомических изображений и на 60-80% для томограмм фантома. Вейвлет-анализ фазово-частотного распределения сигналов обеспечивает лучший результат устранения шума в областях с низким соотношением сигнал/шум, чем в случае фильтрации реконструированных томограмм.

Ключевые слова: томография, вейвлет-анализ, подавление шума, фильтрация, качество изображений.

Kaznacheeva A.O.

PhD in technical sciences, assosiate professor, Saint-Petersburg national research university of information technologies, mechanics and optics

MR IMAGES DENOISING BY MULTILEVEL WAVELET-ANALYSIS

Abstract

This paper presents a technique for magnetic resonance (MR) images processing, which allows to reduce random noise. The technique is based on estimation discrete wavelet transform coefficients in the phase-frequency space data and further image reconstruction. Results estimation applied to the four types of data: acquired not-averaged MR-signal, images reconstructed after k-space wavelet analyses, denoised MR-images, images with multiple signal averaging. It is shown that the wavelet filtering reduces noise by 30% for anatomical images, and 60-80% for phantom images. Wavelet analyses of the raw k-space data provides the best denoising in the areas with low signal-to-noise ratio, than in the case of reconstructed images filtering.

Keywords: MRI, wavelet analysis, denoising, filtering, image quality.

В области неинвазивных исследований внутренней структуры объектов одним из распространенных методов является магнитно-резонансная томография (МРТ). Однако часто высокое временное или пространственное разрешение томограмм достигается за счет соотношения сигнал/шум (SNR). Уровень шума определяется аппаратной частью сканера, методикой сбора данных, природой исследуемого объекта и влияет на сложность интерпретации результатов. Данная проблема особенно актуальна при отображении процессов на молекулярном уровне и визуализации микро-структур. Наиболее распространенным путем снижения шума является усреднение сигнала по нескольким наборам данных, что существенно увеличивает продолжительность исследования. Поэтому одним из направлений развития томографии с высоким разрешением является снижение зашумленности изображений путем их постобработки.

Существует целый ряд методов снижения шума на изображениях, от классической фильтрации Винера [1-2] до современных нейронных сетей [3] и вейвлет-анализа [4-6]. Разложение сигнала по базису, основанному на функции (вейвлета) с  определенными свойствами путем масштабирования и переноса позволяет характеризовать определенную пространственную частоту и ее локализацию в пространстве [7]. Уже первые работы показали, что использование вейвлетов позволяет снизить шум МР-томограмм на 10-50% при сохранении резкости контуров анатомических структур [8].

В подавляющем большинстве работ устранение шума осуществляется на реконструированных изображениях, полученных в результате обратного преобразования Фурье (ПФ) измеренного МР-сигнала. В этом случае шум будет распределен по закону Релея, тогда как в измеренных действительной и мнимой частях фазово-частотного пространства (k-пространства) присутствует аддитивный белый шум, математическое ожидание которого равно нулю. Сравнение эффективности подавления шума с помощью вейвлет-анализа исходных данных k-пространства и непосредственно реконструированного МР-изображения является предметом исследования.

SNR является важным критерием оценки качества любого изображения и характеризует вклад истинной и случайной составляющих в регистрируемый сигнал, который в МРТ зависит от комплекса параметров:

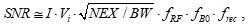
где I – интенсивность сигнала; V_i – объем воксела; NEX – число усреднений сигнала; BW – ширина полосы пропускания; f_RF, f_B0, f_rec – коэффициенты, зависящие от РЧ-катушки, основного поля и алгоритма реконструкции. Для исследований на одном сканере и по одной методике, SNR зависит от размера воксела и количества накоплений измеряемого МР-сигнала:

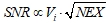
Влияние случайного шума существенно в исследованиях с малым размером воксела [4, 9] или при сверхбыстром сканировании (диффузия, функциональные исследования). В случае ПФ пространственное разрешение определяется шириной РЧ-импульса, однако для анализа нестационарных сигналов ПФ плохо приспособлено. В случае вейвлет-преобразования, разрешение и SNR определяется выбранной базисной функцией 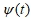, определяющей детали сигнала, и аппроксимирующей функцией 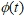, определяющей грубое приближение сигнала. 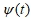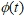Функции  и  уточняются итерационным методом, шаги которого соответствует определенному уровню декомпозиции и восстановления сигнала. Детализирующая функция  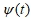создается на основе базисной функции 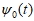, обеспечивающей смещение по оси времени и масштабирование:

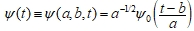
где а – параметр, определяющий ширину пакета; b – его положение.

Для вейвлет-анализа необходимо определить набор двухмерных функций, определяющих вариации коэффициентов разложения: 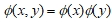для аппроксимирующей функции 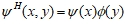,  вдоль столбцов изображения (горизонтальные края объектов),  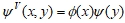вдоль строк (вертикальные края изображений) и  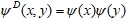вдоль диагоналей. В общем случае для выбранного базиса анализ включает выбор уровня аппроксимации j, глубины разложения N, нахождение коэффициентов разложения на каждом уровне и восстановление исходной функции  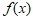при помощи обратного дискретного вейвлет-преобразования:

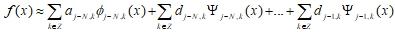
В качестве исследуемой функции выбраны вейвлеты Добеши, обладающие свойствами гладкости и исключения моментов (что позволяет эффективно сжимать сигналы, имеющие большие гладкие области), ортогональности (что позволяет точно восстановить сигнал) и несимметричности. Вейвлеты Добеши строятся на основе функций:

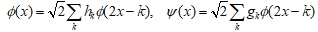
Разложение сигнала с помощью вейвлетов позволяет не только снизить шум, но и выборочно повысить разрешение внутри области сканирования и снизить требования к регистрируемым данным путем ограничения числа областей, требующих высокого разрешения.

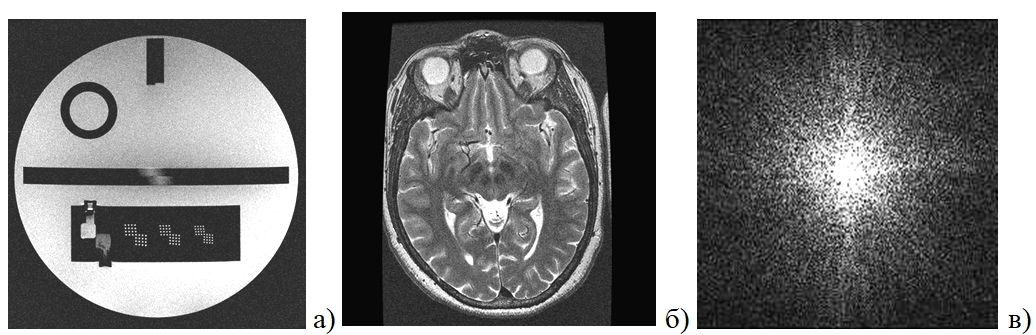
Экспериментальные данные получены на МР-томографе Excite HDxt (General Electric) с полем 3Тл. На первом этапе исследования выполнялись на фантоме для контроля пространственного разрешения томографа (рис. 1а), представляющего заполненную парамагнитным раствором пластиковую форму с тестовым рисунком, содержащим высококонтрастные элементы; для регистрации сигнала использовалась приемо-передающая катушка «птичья клетка». Сбор данных осуществлялся с использованием последовательности быстрое спин-эхо (FSE) с периодом повторения РЧ-импульсов TR=280 мс, временем считывания эхо-сигнала TE=20 мс, толщиной среза th=1 мм, полем сканирования FOV=220´220 мм, матрицей 512´512. Пространственное разрешение составило 0,43 мм. В результате измерений получены два набора: «сырые» данные k-пространства и реконструированные изображения с числом усреднений NEX=1 и NEX=9 (для каждого набора).

На втором этапе эксперимента получены изображения головного мозга (данная группа исследований составляет около 56%). Для регистрации сигнала использовалась объемная 8-канальная катушка. Протокол включал использование импульсной последовательности FSE с параметрами: TR=4000 мс, TE=110 мс, th=2 мм, FOV=220´154 мм, матрица 512´352, пространственное разрешение составило 0,43 мм. Все изображения получены с числом усреднений сигнала NEX=1 и NEX=4, что обеспечивало увеличение SNR в 2 раза; изображения второй группы использованы как эталонные при сравнительной оценке эффективности подавления шума.

Рис. 1 - Обрабатываемые томограммы (а) фантома и (б) головного мозга; (в) k-пространство данных

Обработка данных в формате DICOM выполнялась в среде MatLab 7.0. Аппроксимирующие и детализирующие коэффициенты рассчитывались для вейвлетов Добеши с уровнем разложения 5. Выбор порога τ отсечения детализирующих коэффициентов осуществлялся исходя из степени зашумленности исходных данных. Жесткий порог позволяет сохранить коэффициенты, большие или равные |τ|, а меньшие коэффициенты обнуляются. Мягкий порог обнуляет коэффициенты, меньшие чем |τ|, и снижает остальные на величину |τ|. Оптимизация порога выполнялась с учетом того, что низкое значение сохраняет фон в коэффициентах детализации и поэтому незначительно увеличивает SNR; высокий порог приводит к потере коэффициентов, несущих основную информацию.

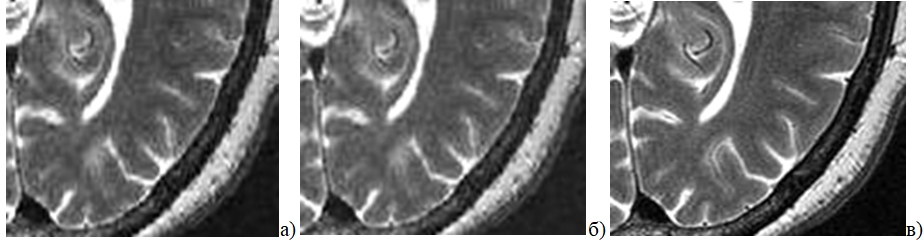
В первом случае, обработка «сырых» данных заключалась в подборе коэффициентов вейвлета Добеши и отсечении белого шума для действительной и мнимой частей k-пространства. Затем с помощью обратного ПФ выполнялась реконструкция изображения (рис. 2а), которое сравнивалось с томограммой при NEX=9 (рис 2в). Во втором случае, вейвлет-анализ и подавление шума выполнялись непосредственно для томограммы (рис. 2б); полученный результат также сравнивался с изображением при 9 усреднениях сигнала. Однако при таком алгоритме обработки, наблюдалось неполное восстановление сигнала в областях с низким SNR. Для всех изображений вейвлеты Добеши обеспечили сохранение резкости на границах контрастных областей, что сделало возможным отображение элементов фантома для оценки пространственного разрешения.

Рис. 2 - Результат подавления шума: (а) фильтрация томограммы (б) фильтрация k-пространства (в) изображение при NEX=9

Существенным отличием анатомических изображений является наличие шума, вызванного физиологическими процессами в организме пациента (пульсация крови, ликвора, дыхание), которые влияют на общий характер распределения шума. В ряде случаев, шум данного типа может быть сопоставим или превышать уровень белого шума. Анализ МР-томограмм головного мозга также выполнялся с помощью вейвлетов Добеши (уровень разложения 5), коэффициенты разложения находились для набора NEX=1, а также для действительной и мнимой частей k-пространства, полученных после ПФ изображения. Визуальная оценка показала, что отсечение детализирующих коэффициентов позволило снизить зернистость структуры и не привело к снижению резкости восстановленного изображения или контрастности граничащих анатомических структур.

Рис. 3 – Подавление шума на изображении головного мозга: (а) фильтрация томограммы (б) фильтрация k-пространства (в) изображение при NEX=4

Количественная оценка результатов выполнялась с помощью среднеквадратического отклонения (СКО) разности изображения, полученного при вейвлет подавлении шума, и изображения при 9 усреднениях сигнала (условно принималось за эталонное в данном эксперименте). СКО рассчитывалось для изображения в целом и для его отдельных однородных областей. Первая область (R1) размером 50×50 пикселов была выбрана в левом верхнем углу изображения за пределами фантома и соответствовала шуму фона со среднем значением интенсивности 188±91. Область R2 аналогичного размера была выбрана в правой верхней четверти изображения фантома и соответствовала однородному сигналу парамагнитного раствора со средней интенсивностью 2029±134.

При подавлении шума в k-пространстве СКО для реконструированного изображения фантома в области R1 уменьшилось на 73% и составило 25,7; для области R2 значение СКО уменьшилось на 22,3% и составило 70,6. При подавлении шума непосредственно на томограмме фантома, вейвлет-анализ позволил снизить зашумленность на 26% (среднее значение шума на обработанном изображении составило 114, на исходном - 153). В этом случае для области R1 среднеквадратическое отклонение уменьшилось на 77% и составило 21; для области R2 значение СКО снизилось на 54,5% и составило 62. На нескольких изображениях после их восстановления из k-пространства наблюдались артефакты; среднее значение сигнала во всех случаях менялось незначительно.

Оценка подавления шума на МР-томограммах головного мозга включала расчет среднего арифметического значения и СКО для разности изображения, полученного после вейвлет-фильтрации, и изображения, полученного при 4 усреднениях сигнала. Оценка выполнялась для однородной области R3 размером 50×50 пикселов, расположенной в левой нижней четверти изображения за границами объекта (уровень шума составил 208±82). Вейвлет-анализ k-пространства позволил снизить СКО для области R3 на 78%, что составило 7,4 (для разности зашумленного изображения и изображения при NEX=4 значение СКО=69). При устранении шума непосредственно на томограмме, вейвлеты Добеши снижали СКО шума для разности обработанного изображения и изображения при NEX=4 до 63,6 (около 28%). В этом случае для области R3 среднеквадратическое отклонение уменьшилось на 78% и составило 7,4.

Таким образом, во всех случаях, при вейвлет-анализе анатомических изображений выбор одинаковых порогов и уровней разложения давал меньшое снижение шума, что можно объяснить более сложной природой шума, в частности, наличием физиологического шума и его периодичностью.

Многоуровневый вейвлет-анализ МР-томограмм на основе вейвлетов Добеши является эффективным средством подавления шума и повышения качества изображений. Основной задачей работы являлось применение вейвлетов к действительной и мнимой частям данных k-пространства и сравнение реконструированного изображения с результатом аналогичной фильтрации, применяемой непосредственно к МР-томограмме и используемой в настоящее время для обработки изображений. Сравнение предлагаемого метода и традиционного показало их отличие для областей с низким SNR, где лучший результат шумоподавления достигается в первом случае.

Для анатомических изображений в большинстве случаев достигается снижение шума на 30%, что соответствует сокращению продолжительности сканирования в 2 раза или повышению пространственного разрешения на соответствующую величину. Для изображений фантомов, не являющихся источниками шума, эффективность шумоподавления составляет 63-80%, что также объясняется относительной однородностью их структуры и существенно более узким диапазоном интенсивностей сигналов.

Рассмотренный метод может быть эффективен для анализа результатов функциональных МРТ-исследований, характеризующихся достаточно низким пространственным разрешением и соотношением сигнал/шум. Предметом отдельного исследование может стать изучения влияния алгоритма обработки на результат фильтрации, например, использование таких дополнительных этапов постобработки, как пороговая сегментации, адаптивная фильтрация, методы выделения границ и т.п. Вейвлет-анализ также будет эффективен для снижения шума в 3D-наборах срезов, где сбор данных осуществляется от отображаемого объема в целом и можно предположить, что одновременное подавление шума для всего объема данных повысит диагностическую ценность исследования.

Литература

1. Martin-Fernandez M., Alberola-Lopez C., Ruiz-Alzola J., Westin C.F. Sequential anisotropic Wiener filtering applied to 3D MRI data // Magnetic Resonance Imaging. - 2007. - Vol. 25. - P. 278-292.
2. Захаров Д.Д., Сизиков В.С., Шемплинер В.В., Щекотин Д.С. Новые способы устранения артефактов на томографических и иных изображениях // Научно-технический вестник ИТМО. - 2006. - №32. - С. 138-143.
3. Коршаков А.В., Шатерников В.Е. Повышение эффективности эксплуатации МР-томографов на основе усовершенствованных алгоритмов формирования изображений // Врач-аспирант. - 2008. - №1. - С. 65-74.
4. Казначеева А.О. Разработка методов и средств шумоподавления в томографии: Автореф. дис. канд. техн. наук. - Санкт-Петербург, 2006. - 19 с.
5. Alexander M.E. et. al. A wavelet-based method for improving signal-to-noise ratio and contrast in MR images // Magnetic Resonance Imaging. - 2000. - Vol. 18. - P. 169-180.
6. Казначеева А.О., Власюк А.В., Кудряшов А.В. Возможности вейвлет-преобразований в повышении точности измерений параметров диффузии в МРТ // Научно-технический вестник ИТМО. - 2009. - №5. - С. 86-91.
7. Астафьева Н.М. Вейвлет-анализ: основы теории и примеры применения // Успехи физических наук. - 1996. - Т. 166, №11. - С. 1145-1170.
8. Weaver J.B., Xu Y, Healy D.M., Cromwell L.D. Filtering noise from images with wavelet transforms // Magnetic Resonance Imaging. - 1991. Vol. 21. - P. 288-95.
9. Трофимова Т.Н., Медведев Ю.А., Ананьева Н.И. и др. Использование посмертной магнитно-резонансной томографии головного мозга при патолого-анатомическом исследовании // Архив патологии. - 2008. - Т. 70. № 3. - С. 23-28.