CALCULATION OF OPERATIONAL PARAMETERS OF SUPERCAVITATION EVAPORATOR

Кулагин В.А.¹, Пьяных Т.А.²

¹Доктор технических наук, профессор, ²аспирант, Сибирский федеральный университет

РАСЧЕТ РЕЖИМНЫХ ПАРАМЕТРОВ СУПЕРКАВИТАЦИОННОГО ИСПАРИТЕЛЯ

Аннотация

В данной работе на основе математического моделирования проведена оценка режимных параметров СК-испарителя.

Ключевые слова: кавитация, СК-испаритель, математическая модель.

Kulagin V.A. ¹, Pyanykh Т.А.²

¹Doctor of Technical Science, Professor, ²postgraduate student, Siberian Federal University

CALCULATION OF OPERATIONAL PARAMETERS OF SUPERCAVITATION EVAPORATOR

Abstract

In this paper assessment of operational parameters of SС-evaporator performed on the basis of mathematical modeling.

Keywords: cavitation, SС-evaporator, the mathematical model.

В связи с высокими требованиями, предъявляемыми к качеству воды, используемой в энерготехнологическом комплексе, исходную воду подвергают физико-химической обработке, в результате которой образуется значительное количество высокоминерализованных сточных вод, объем которых напрямую зависит от применяемой технологии водоподготовки.

Заметные экологические преимущества, свойственные термическому методу водоподготовки, а также возможность переработки с его помощью промышленных минерализованных сточных вод значительно повысили интерес к этому методу водоподготовки. Однако этот метод обладает рядом существенных недостатков: высокой степенью накипеобразования, малой энергонапряженностью поверхности теплообмена, большими габаритами. Улучшение указанных характеристик наблюдается при применении суперкавитирующих (СК) испарителей [1]. Идея кавитационного метода интенсификации тепломассообмена заключается в том, что при обтекании недогретой жидкостью кавитаторов различной формы в рабочем модуле СК-испарительных камер образуются суперкаверны, из которых производится пароотбор, (Рис. 1).

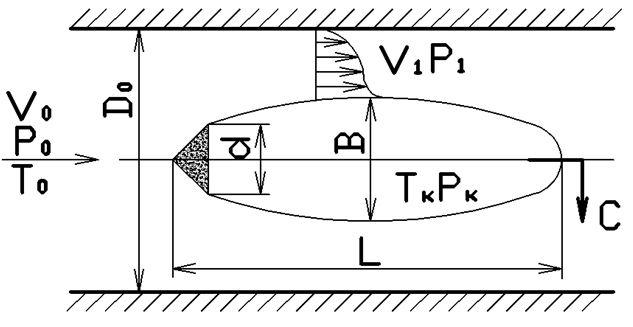
Рис. 1 - Физико-механическая модель СК-испарения

 

В данной работе на основе математического моделирования проведена оценка режимных параметров СК-испарителя.

Математическая модель СК-испарителя

Для моделирования рабочих процессов СК-испарителя использовалась модель двухфазного гомогенного потока. Эта модель основывается на предположении локального кинематического и термодинамического равновесия между фазами и не предполагает поверхность раздела между паром и водой. Также мы пренебрегаем выделением тепла за счет вязкостного трения, принимается, что температурное поле определяется только испарением и конденсацией. Кавитационное течение жидкости в этом случае описывается уравнениями неразрывности, сохранения момента импульса, уравнением сохранения энергии и уравнением переноса жидкой фазы, представленными в стационарном виде ниже [2]:

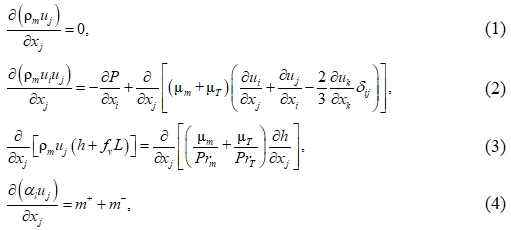
где 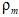 – плотность смеси; L – теплота парообразования;  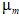– коэффициент динамической вязкости смеси; P – давление; h – удельная энтальпия жидкости;  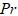– число Прандтля.

Теплофизические параметры смеси 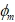 и массовая доля пара  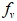определяются, соответствующими выражениями

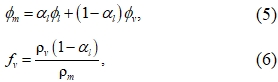
где 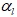  – объемная доля жидкости.

Источниковый 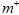 и стоковый  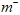члены в уравнении (4) определяют, соответственно, скорости испарения и конденсации воды. Основываясь на уравнении Рэлея-Плессета, учитывающего вязкость жидкости и поверхностное натяжение при пульсациях пузырька в жидкости, получены следующие выражения:

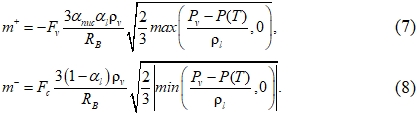
Эмпирические постоянные 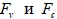 в этих уравнениях учитывают тот факт, что процессы конденсации и испарения имеют различные временные масштабы. Для расчетов принимались следующие значения: объемная доля неконденсированного газа в воде  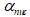равна 5·10^-5, а радиус зародышей кавитации .

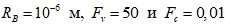Для учета турбулентности использовалась 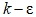 модель. Уравнения переноса кинетической энергии турбулентности k и ее диссипации ε имеют вид:

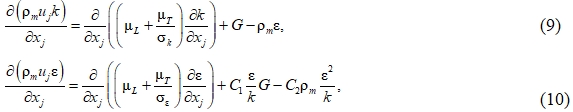где  скорость генерации турбулентности G и тензор напряжений Рейнольдса определяются по соответствующим уравнениям: 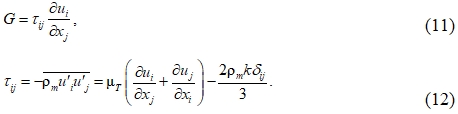Турбулентная вязкость  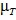определяется по формуле:

Эмпирические константы имеют следующие значения: .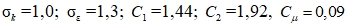

Объемная доля фазы может изменяться от нуля до единицы, в зависимости от занимаемого пространства в двухфазном потоке. Согласно тому, что фазы должны полностью заполнять весь объем, получим уравнение:

Апробация предложенной математической модели представлена в [3].

Геометрия и граничные условия

На (Рис. 2) представлена геометрия рабочего участка СК-испарителя с обозначением граничных условий. В рабочем участке длинной Н = 470 мм и диаметром D₀ = 70 мм установлен кавитатор на расстоянии h = 50 мм от входа в рабочий участок. В качестве кавитатора использовался конус. Исследования проводились в условиях, когда влияние стеснения потока на форму и размеры каверны существенно. Степень стеснения потока d/D₀ принималась равной 0,457. Через трубку, расположенную вдоль оси рабочего участка, осуществлялся отбор пара из каверны.

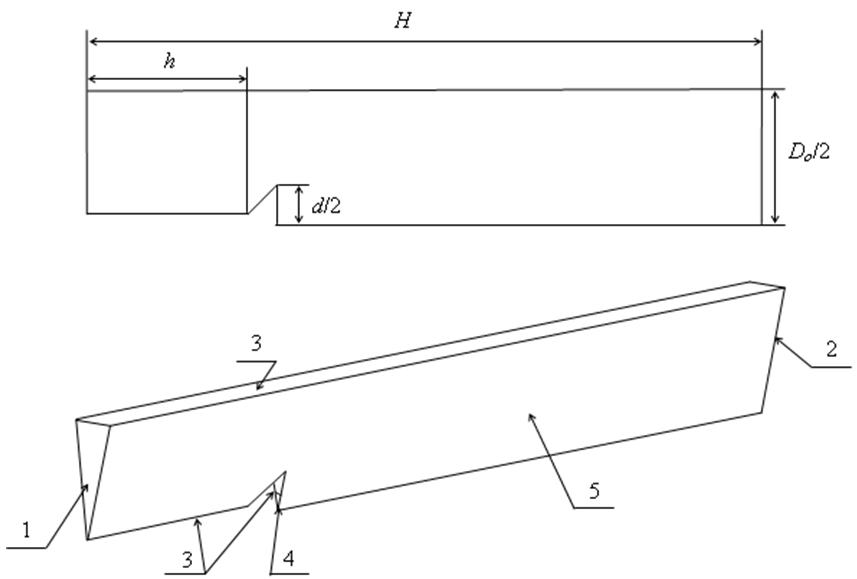
Рис. 2 - Геометрия рабочего участка суперкавитационного испарителя с обозначением граничных условий: 1 и 2 соответственно вход и выход из рабочего участка, 3 – стенки, 4 – отбор пара из каверны, 5 – условия симметрии

Задача решалась в стационарной осесимметричной постановке. Для замыкания системы уравнений принимались следующие граничные условия: на входе в рабочий участок задавалась скорость, линейный масштаб и интенсивность турбулентности, объемные доли пара и воды 0,0 и 1,0, соответственно, а на выходе – давление. На стенках скорость задавалась равной нулю. Расчеты проводились для воды, температура которой принималась равной 110 и 120 °С. В основании кавитатора осуществлялся отбор пара.

Результаты численного исследования

На (Рис. 3) представлены зависимости максимально возможного пароотбора от числа кавитации при различных числах Фруда и температурах.

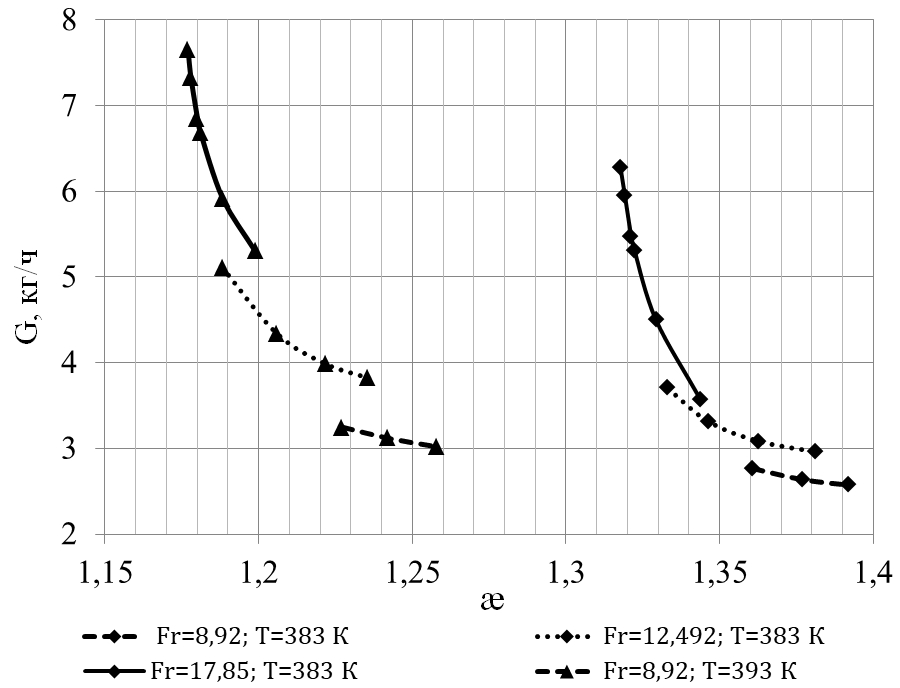
Рис. 3 - Зависимости максимально возможного пароотбора от числа кавитации при различных числах Фруда и температурах

Под максимально возможным пароотбором понимается отбор пара из каверны предельной длины, равной диаметру кавитатора. При дальнейшем увеличении пароотбора наблюдается брызгоунос с отбираемым из каверны паром, что будет существенно влиять на качество получаемого дистиллята.

Как видно из графиков, с увеличением чисел Фруда, температуры и уменьшением чисел кавитации величина максимально возможного пароотбора увеличивается.

Представленные зависимости могут быть использованы при проектировании СК-испарителей.

Литература

1. Ивченко В.М., Кулагин В.А., Немчин А.Ф. Кавитационная технология: монография. Красноярск: Изд-во КГУ, 1990. 200 с.
2. Tseng C.-C., Shyy W. // International Journal of Heat and Mass Transfer, 53 (2010) 513–525.
3. Кулагин В.А., Пьяных Т.А. // Journal of Siberian Federal University. Engineering & Technologies, Numerical Methods in Fluids, 1 (2012 5) 57-62.