DIRECT AND INVERSE PROBLEMS KINEMATICS OF THE ORIGINAL PART OF THE MANIPULATOR OF SIX-DEGREE-OF-FREEDOM

Балакин П. Д.¹, Шамутдинов А. Х.²

¹Доктор технических наук, профессор, заведующий кафедрой ТММ; ²Старший преподаватель кафедры ТММ.

Омский государственный технический университет

ПРЯМАЯ И ОБРАТНАЯ ЗАДАЧИ КИНЕМАТИКИ ОРИГИНАЛЬНОЙ ЧАСТИ ШЕСТИКООРДИНАТНОГО МАНИПУЛЯТОРА

Аннотация

Геометрически решена прямая задача кинематики, а при q₁ = q₂ − обратная задача кинематики оригинальной части шестикоординатного манипулятора.

Ключевые слова: манипулятор, абсолютная система координат, обобщенные координаты, рабочий орган манипулятора.

Balakin P.D. ¹, Shamutdinov A.H. ²

¹Doctor of Technical Sciences, Professor, Head of Department of TMM; ²Senior teacher of faculty of TMM.

DIRECT AND INVERSE PROBLEMS KINEMATICS OF THE ORIGINAL PART OF THE MANIPULATOR OF SIX-DEGREE-OF-FREEDOM

Abstract

Geometrically solved by kinematics of the direct problem, and if q₁ = q₂ - inverse kinematics problem of the original part the manipulator of six-degree of freedom.

Keywords: the manipulator, the absolute system of coordinates, the generalized coordinates, the working body of the manipulator.

Прямая задача для манипулятора – это вычисление положения (x_р, y_р, z_р) рабочего органа манипулятора по его кинематической схеме и значениях обобщенных координат (q₁, q₂… q_n) , где n – число степеней свободы манипулятора, q_i – обобщенные координаты.

Обратная задача – это вычисление величин обобщенных координат (q₁, q₂… q_n) по заданному положению (x_р, y_р, z_р) рабочего органа при известной схеме кинематики манипулятора.

Прямую задачу кинематики манипулятора [1] будем решать геометрически. Для этого изобразим кинематическую схему манипулятора, обобщенные координаты его звеньев q_n, их длины l_n и привяжем к манипулятору абсолютную (неподвижную) систему координат (X,Y,Z), обозначив координаты рабочего органа x_р, y_р, z_р (рис. 1).

Обозначения на рис. 1: (X,Y,Z) – абсолютная (неподвижная) система координат; Р – точка, где находится рабочий орган (заготовка, инструмент) на рабочем столе; P′ – положение рабочей точки Р при вращении блока звеньев (2, 4 – 8) вокруг оси параллельной оси X в т. О₁; P′′ – положение рабочей точки Р при вращении блока звеньев (2, 5 – 8) вокруг оси параллельной оси X в т. О₄′′= О₄′′′; (x,y,z) – координаты т. Р; (x′,y′,z′) – координаты т. Р′; (x′′,y′′,z′′) – координаты т. Р′′; (x_р, y_р, z_р) – координаты т. Р′′′; O₁P′∙= O₁P = l_p; O₄′P′ = O₄′P′′ = O₄P = l_p′; O₁O₄′ = O₁O₄ = b.

Позиции на рис. 1: 1 − Поворотный стол; 2 − Левый стержень (двигатель поступательного перемещения); 3 − Верхний стержень (двигатель поступательного перемещения); 4 – Опоры; 5 – Рабочий стол; 6 − Опорно-поворотное устройство; 7 − Наклонная платформа; 8 − Правый стержень (двигатель поступательного перемещения).

Последовательность поворотов стержней 2 и 3 не меняет итоговое положение рабочего стола 8. По аналогии видно, что последовательность поворотов стержней 2, 3 и поворотного стола 1 также не изменяет итогового положения рабочего стола 8. Поэтому будем изменять, например, положение, сначала стержня 3, потом стержня 2 и потом положение поворотного стола 1.

По заданным обобщенным координатам найдем положение точки P рабочего органа. Из рис. 1 видно, что первоначальные координаты т.Р будут:

x = 0, y = – l₃∙cos β; z = H

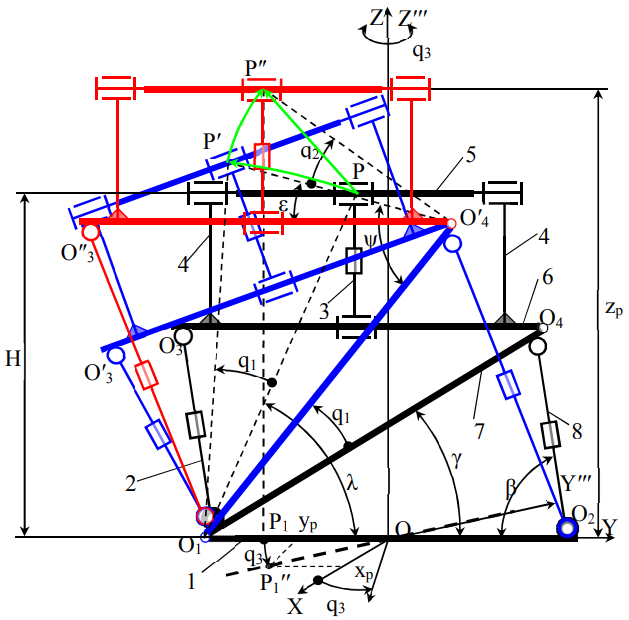
Рис. 1. Кинематическая схема манипулятора

При изменении обобщенной координаты q₁ (повороте) т. Р займет положение Р′. Представим вращение треугольника O₁P′P вокруг начала координат О: сначала нужно его повернуть против часовой стрелки на угол q₁, а потом параллельным переносом по оси Y сместить влево на величину а/2 (рис. 2). Из рис. 2 видно:

x′ = 0, y′ = O₁P′∙cos(q₁ + λ) – a/2, z = O₁P′∙sin(q₁ + λ)

или x′ = 0, y′ = l_p′∙cos(q₁ + λ) – a/2, z = l_p′∙sin(q₁ + λ),

где λ – угол наклона линии O₁P относительно горизонтали.

При изменении обобщенной координаты q₂ (повороте) т. Р′ займет положение Р′′. Представим вращение треугольника O₄′P′P″ вокруг начала координат О: сначала нужно его повернуть по часовой стрелки на угол q₂, потом параллельным переносом сместить вправо на величину y₁ и наконец

Рис. 2. Поворот манипулятора на угол q₁

параллельным переносом по оси Z переместить вверх на величину h₁ (рис. 3):

x′′ = 0, y′′ = – O₄′P′′∙cos(q₂ + ε) + x₁, z′′ = O₄′P′′∙sin(q₁+ε) + h₁

или x′′ = 0, y′′ = – l_p′∙cos(q₂+ε) + x₁, z′′ = l_p′∙sin(q₂ + ε) + h₁,

где ε – угол наклона линии O₄′P′∙относительно горизонтали,

x₁ = b∙cos(q₁ + γ) – a/2, h₁ = b∙sin(q₁ + γ)

Из треугольника О₁Р′О₄′ (рис. 1) по известной теореме находим:

O₁P′² = O₄′P′² + O₁O₄′² – 2O₄′P′∙O₁O₄′∙cos ψ или l_p² = l_p′² + b²-2b∙l_p′∙cos ψ, откуда

. Из рисунка видно, что ε = ψ - q₁- γ

При вращении манипулятора (системы XYZ) вокруг оси Z ≡ Z′′′ (рис. 1) координаты т.Р′′′ будут: x_р = y′′ sinq₃, y_р = y′′∙cosq₃, z_р = z′′.

Рис. 3. Поворот манипулятора на угол q₂

Окончательно можно записать:

x_p = [- l_p′∙cos(q₂ + ψ – q₁ – γ) + b∙cos(q₁+γ) – a/2]∙sinq₃,

y_p = [- l_p′∙cos(q₂ + ψ – q₁ – γ) + b∙cos(q₁+γ) – а/2]∙cosq₃,                                      (1)

z_p = l_p′∙sin(q₂+ ψ – q₁ – γ) + b∙sin(q₁+γ).                          

Таким образом, прямая задача кинематики для данного манипулятора – решена, что позволяет определить положение рабочего органа манипулятора при заданных значениях обобщенных координат для любого момента времени.

Из соотношений (1) видно, что решение обратной задачи в явном виде невозможно. Для нашего случая, когда q₁ = q₂, для итогового положения рабочего органа манипулятора решение обратной задачи не представляет сложности. Запишем соотношения (1) при q₁ = q₂:

x_p = [- l_p′∙cos(ψ – γ) + b∙cos(q₁+γ) – a/2]∙sinq₃,

y_p = [- l_p′∙cos(ψ – γ) + b∙cos(q₁+γ) – a/2]∙cosq₃,                                                     (2)

z_p = l_p′∙sin(ψ – γ) + b∙sin(q₁+γ).

Из первых двух уравнений имеем:

Из третьего уравнения находим:

Окончательно запишем:

                                      (3)

ВЫВОДЫ:

1. Для исследуемой схемы механизма манипулятора аналитически решена прямая задача кинематики (1), что позволит, для каждого момента времени, определить положение исполнительного органа манипулятора и выбрать схему нагружения для определения усилий, действующих на манипулятор.
2. При q₁ = q₂ – решена обратная задача кинематики (3);
3.  Эти задачи могут быть решены и при иных условиях или модификациях схемы.