DECISION MAKING SUPPORT FOR ENERGY FACILITIES SITING

Шакиров В.А.¹, Панкратьев П.С.²

¹Кандидат технических наук, доцент, ²аспирант, Братский государственный университет

ПОДДЕРЖКА ПРИНЯТИЯ РЕШЕНИЙ ПРИ ВЫБОРЕ ПУНКТОВ СТРОИТЕЛЬСТВА ЭНЕРГЕТИЧЕСКИХ ОБЪЕКТОВ

Аннотация

В статье формулируется проблема выбора пунктов строительства энергетических объектов. Рассмотрен подход к сравнению по многим критериям пунктов строительства энергетических объектов. Проведен краткий обзор и выбор методов для анализа.

Ключевые слова: принятие решений, размещение энергетических объектов, многокритериальный анализ.

Shakirov V.A.¹, Pankratyev P.S.²

¹ PhD in technical science, associate professor, ²postgraduate student, Bratsk State University

DECISION MAKING SUPPORT FOR ENERGY FACILITIES SITING

Abstract

In the article the problem of siting of energy facilities is formulated. An approach to multi criteria ranking of sites of energy facilities is considered. Multi criteria decision making methods are considered and chosen.

Keywords: decision making, siting of energy facilities, multi criteria analysis.

Принятие решений по строительству новых энергетических объектов в районе, как правило, осуществляется в условиях неполной информации, многочисленных критериев оценки. По ряду критериев проведение точной количественной оценки нецелесообразно в силу ограниченности финансовых и временных ресурсов. Зачастую такие задачи уникальны, что требует индивидуального подхода к формализации проблемы и применению методов системного анализа. Особый интерес представляют предпроектные решения, которым в большей степени присущи описанные выше сложности. В то же время, предпроектные решения во многом определяют последующие шаги, этапы реализации инвестиционных программ, имеют долговременные социальные, экологические, экономические последствия. Для повышения качества принимаемых решений используются системы поддержки принятия решений. На основе диалоговых процедур с лицом, принимающим решения (ЛПР),  проводится формализация его предпочтений и многокритериальная оценка альтернатив. В статье предлагается подход к выбору пунктов строительства энергетических объектов на основе двух методов многокритериального анализа.

Под пунктом строительства энергетического объекта будем понимать точку на местности в достаточно обширном районе площадью от сотен до десятков тысяч квадратных километров, в окрестностях которой впоследствии может быть выбрана площадка для строительства.

Как правило, каждый пункт обладает определенным экономическим, экологическим и социальным окружением. Поэтому в каждом пункте могут быть реализованы только определенные варианты энергетического объекта. Если рассматривать строительство тепловой электростанции (ТЭС), то в каждом пункте может быть намечен возможный диапазон мощности, который определится в зависимости от прогнозируемой электрической нагрузки, ресурсной обеспеченности (топливом, водой и т.п.), экологических ограничений и т.п. Каждый вариант мощности станции будет создавать определенное экономическое, экологическое и социальное воздействие в месте строительства. Поэтому целесообразно проводить выбор пунктов с оценкой качества возможных последующих решений.

Задачу принятия решений сформулируем следующим образом. Пусть А={a₁, a₂,…,a_k} множество пунктов строительства энергетических объектов, которые оцениваются по множеству критериев . Каждому пункту (элементу множества A) в соответствие ставится множество B_i={b_i1, b_i2, ..., b_im},  вариантов реализации энергетического объекта. Альтернативы множеств B_i оцениваются только по множеству критериев G={g₁, …, g_p}, . Необходимо упорядочить альтернативы множества A по предпочтению с учетом многокритериальных оценок альтернатив множеств B_i. На рис. 1 представлена иллюстрация сформулированной задачи.  

Рис. 1. Задача выбора пункта строительства энергетического объекта с анализом последующих решений

Выделение из множества критериев F множества G  обусловлено тем, что варианты энергетического объекта оцениваются только по части критериев из критериев F (рис. 1, 2). Кроме того, можно отметить различие в том, как выражены критерии множеств F₁ и G. Например, рассмотрим иерархию целей и критериев при выборе пункта строительства ТЭС.

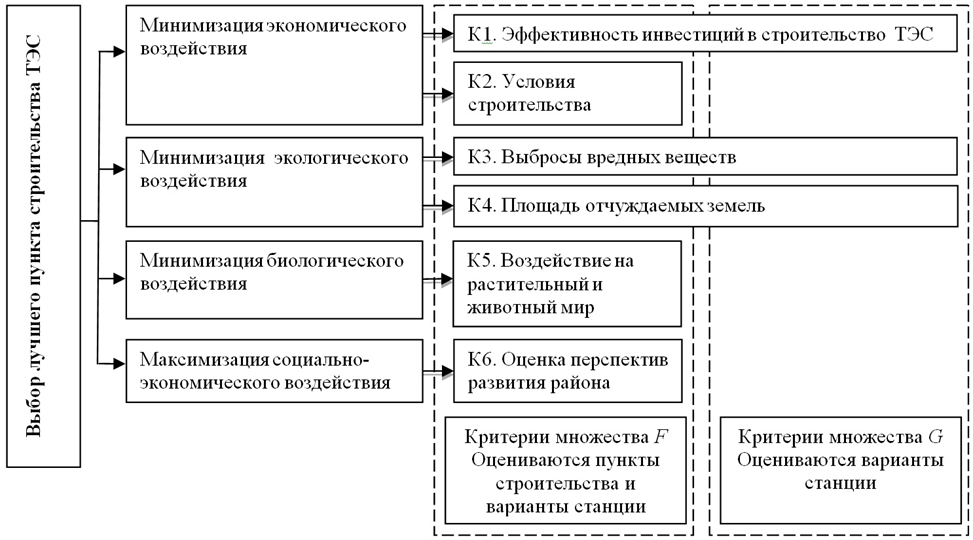
Рис. 2. Иерархия целей и критериев при выборе пункта строительства ТЭС

По критериям множества G (К1, К3, К4) оцениваются варианты ТЭС. Как правило, они имеют количественное выражение. По критериям множества F (К1 – К6) оцениваются пункты строительства. Критерии имеют как количественное, так и качественное выражение (К2, К5, К6).

Предлагается следующий подход к выбору пункта строительства энергетического объекта. На первом этапе оцениваются по критериям множества G все варианты энергетического объекта, которые можно реализовать в пунктах. Для каждого пункта, с учетом предпочтений ЛПР, выбираются лучшие варианты энергетического объекта. Затем проводится сравнение пунктов по критериям множества F. В качестве оценок по критериям множества G принимаются параметры выбранных лучших энергетических объектов.

Проведем выбор метода для анализа вариантов энергетических объектов по критериям множества G. Как правило, при анализе будут превалировать критерии с количественным выражением. Количество альтернатив может достигать нескольких сотен. В таких условиях эффективен метод MAUT [1]. Данный метод широко применялся на практике [2]. Методы, основанные на парных сравнениях, такие как метод анализа иерархий (МАИ) [3], группа методов ELECTRE [4] не будут эффективны, так как при большом количестве альтернатив парные сравнения вызывают значительные затраты усилий ЛПР, проблему согласованности ответов.

MAUT имеет аксиоматическое обоснование [2, 5]. При выполнении условий-аксиом дается математическое доказательство существования скалярной функции полезности u(y), которая ставит в соответствие каждой альтернативе число, отражающее ее полезность. При выполнении условий взаимной независимости критериев по полезности, может быть получена многокритериальная функция полезности в аддитивном (1) или мультипликативном виде (2) [2]:

где u_i(y_i) – однокритериальная функция полезности; y_i – оценка альтернативы по критерию i; k_i – шкалирующий коэффициент критерия i; k – шкалирующий коэффициент.

Проведем выбор метода для анализа пунктов строительства. Поскольку в анализе используются критерии с количественным и качественным выражением, а количество альтернатив, как правило, не превышает десяти, эффективен метод МАИ. Данный метод также широко применялся на практике [3]. Методы вербального анализа будут не столь эффективны из-за наличия критериев с количественным выражением [4].

В соответствии с МАИ [3], ЛПР проводит попарные сравнения всех критериев с помощью шкалы относительной важности (таблица 1), формируя матрицу парных сравнений. Затем проводится парные сравнения альтернатив отдельно по каждому критерию.

Таблица 1 – Относительная шкала сравнения

Уровень важности	Количественное значение
Равная важность	1
Умеренное превосходство	3
Значительное превосходство	5
Явное превосходство	7
Абсолютное превосходство	9

Так формируются матрицы парных сравнений альтернатив. Вычислив собственные вектора матриц парных сравнений, проведя нормирование элементов собственных векторов, можно получить веса критериев и альтернатив [3]. Оценки альтернатив с учетом всех критериев получают по выражению:

где V_j – показатель качества j-й альтернативы; w_i – вес i-го критерия; v_ij – вес j-й альтернативы по i-му критерию.

Предлагаемый подход к выбору пунктов строительства может применяться для поддержки принятия решений в предпроектном анализе, в условиях, когда о сооружаемом объекте отсутствуют точные данные. Такими объектами могут быть как энергетические (ГЭС, ТЭС, АЭС и прочие), так и объекты производственного назначения (в химической и нефтехимической, лесной и деревообрабатывающей промышленности, заводы тяжелого машиностроения и т.д.).

Предложенный подход многокритериального анализа пунктов строительства может быть реализован в виде системы поддержки принятия решений при оценке инвестиционных решений, при перспективном планировании.