ON APPLYING THE CORRELATION AND REGRESSION TECHNIQUE IN AN ENTERPRISE COSTS MANAGEMENT PROBLEM
ON APPLYING THE CORRELATION AND REGRESSION TECHNIQUE IN AN ENTERPRISE COSTS MANAGEMENT PROBLEM
Abstract
In the paper, the problem of analysis of changing the self-cost value of products of processing agricultural enterprises regarding costs changes of producing is studied. The investigation of the problem is based on methods of theoretical and statistical analysis and mathematical modeling. The dependence to be examined is mathematically modelled as a directly proportional dependence between the average statistical accession costs rate of production and its self-cost index. Within the mathematical model under consideration, it is stated that the relationship being studied is correlative and the correlation dependence structure is established as nonlinear regression. Materials of data processing are deduced by graphs to illustrate basic results obtained in the paper for fruit and vegetable processing enterprises.
1. Введение
Проблема управления затратами на предприятии всегда представляла интерес для экономистов, поскольку её решение позволяет достигнуть нужного экономического результата, оценить эффективность в целом работы предприятия и сделать его работу более устойчивой в условиях конкуренции. Указанная проблема изучалась в ряде публикаций последних лет, как в России, так и за рубежом. Проблемы управления стоимостью и анализ затрат на предприятии рассматривались ранее в отечественных и зарубежных публикациях, начиная с XX века, среди которых, в том числе, следует отметить работы Денисовой И.П., Лебедева В.Г., Дроздовой Т.Г., Кустарева В.П., Танака Т., Шим Д.К., Сигел Д.Г. , , , и др.
В условиях неустойчивой экономики перед каждым предприятием стоит задача обеспечения стабильной конкурентоспособности продукции и, как следствие, обоснованное изменение оптовых цен, соответствующих текущему платежеспособному спросу. Поэтому первоочередной задачей в деятельности современного предприятия является проблема управления затратами, позволяющая провести анализ изменения себестоимости продукции. В последние десятилетия актуальность данной проблемы обсуждалась на различных научных конференциях (например и др.), и рассматривалась в работах Друри К., Наугольновой И.А., Зыковой Т.Б., Белокуренко Н.С., Артемовой Е.В., Постникова В.П. , , , и др. Многофакторность данной проблемы порождает разнообразие подходов и методов её решения, среди которых эконометрические методы корреляционно-регрессионного анализа занимают особое место , . Как известно, эти методы позволяют выявить силу взаимосвязи различных факторов, дать оценку факторов, в наибольшей степени оказывающих влияние на результативный признак, выбрать форму связи факторных и результативных признаков, а также предложить тип математической модели для прогнозирования значений этих признаков. Наличие статистической взаимосвязи между указанными факторами очевидна, однако аналитическая структура этой связи всегда требует дополнительного анализа, а её характер и теснота в каждом конкретном случае устанавливается лишь на основе специальной статистической обработки результатов наблюдений.
Вопросы изменения себестоимости под влиянием различных факторов (например, объем выпуска, трудоёмкость единицы продукции, оптовая цена энергоносителя, доля прибыли, изымаемой государством и др.) изучались в работах , , , , где дан анализ тесноты корреляционной связи факторов и построены различные регрессионные модели, представляющие эту связь. Вместе с тем, сравнение результатов прогнозирования значений результативного признака с помощью построенных как линейных, так и нелинейных моделей показывает различную степень их адекватности моделируемому объекту. Это порождает проблему выбора наиболее адекватной модели среди различных предлагаемых моделей.
Целью настоящей работы является разработка метода исследования характера статистической взаимосвязи между безразмерными экономическими показателями (индексом изменения себестоимости продукции и темпов изменения затрат на её производство) на основе идей индексного и корреляционно-регрессионного статистического анализа , . Ставится задача построения метода математического моделирования , , , позволяющего предложить наиболее адекватную модель этой связи в рассматриваемом случае, а также дать оценку возможных перспектив применения предлагаемого подхода при построении экономико-математической модели для анализа характера изменения себестоимости продукции перерабатывающих предприятий сельского хозяйства.
2. Постановка задачи и описание метода
Для изучения указанной проблемы будем рассматривать математическую модель описанного выше процесса в предположении следующего условия взаимосвязи: среднее изменение себестоимости продукции прямо пропорционально среднему изменению затрат на её производство. Под себестоимостью в дальнейшем будем понимать себестоимость одной условной единицы продукции. В данной математической модели предполагается, что наименования продукции и количество наименований остаются неизменными в анализируемом промежутке времени. Будем обозначать символом ζ среднюю величину изменения себестоимости в процентах, определяемую изменением затрат. Тогда, если значение себестоимости в начальном периоде равно z0 то в результате изменения затрат новые значения себестоимости z ̃0, z ̃1 будут иметь вид:
где Δz0,1=0,01ζ1,2 z0,1.
Запишем выражение агрегатного индекса затрат (суммирование осуществляется по всем наименованиям продукции)
:где q0, ζ1– объем выпуска и изменения (в процентах) себестоимости продукции в начальном периоде I, величины q1, ζ2 – объем выпуска и изменения (в процентах) себестоимости продукции в последующем периоде II. Тогда величины текущих затрат С ̃0,(С ̃1 c учетом их изменений в начальном и текущем периодах можно представить в виде:
Учитывая сказанное, будем считать, что принятое выше предположение о пропорциональности применяется для средних значений изменения себестоимостей ζ1,2 и среднестатистических приростов затрат ,
в предыдущих и последующих периодах:
Тогда получим два соотношения (λ – некоторых свободный параметр):
Пусть за 2 периода известна информация о себестоимостях и объемах выпуска n наименований продукции первого периода I и второго периода II. Следуя , для указанной информации сформируем векторы себестоимостей и векторы объемов выпуска продукции n наименований:
Тогда можно сформировать матрицы
В результате перемножения указанных матриц c учетом правил матричного формализма (3) получим матрицу затрат :
В соотношении (4) символ Q' обозначает, транспонированную Q матрицу, Cij – реальные (при i=j) и условные (при i ≠ j) затраты на производство продукции заданных наименований. Тогда приросты затрат, средневзвешенные по величинам себестоимостей первого и второго периодов ζ1,2, можно представить выражениями:
При этом соотношения (1) принимают вид
В результате приходим к следующей системе линейных алгебраических уравнений (λ – параметр, подлежащий определению)
3. Полученные результаты
В результате применения операций матричного формализма приходим к задаче решения матрично-векторного уравнения С•ζ=λζ для нахождения собственных значений λ и собственных векторов ζ преобразованной матрицы С затрат.
Как известно, собственные значения λ в общем виде определяются решениями характеристического уравнения для матрицы С (E - единичная матрица):
Отыскание собственных значений из характеристического уравнения (6) в преобразованном виде приводит к выражениям (C22≥C11)
При отыскании собственных векторов из соотношений (5) с учетом (7) оказывается, что требованиям λ, ζ1, ζ2>0может удовлетворять лишь собственное значение λ+, которое для любых условий остается положительным и порождает допустимые векторы изменения себестоимости (собственные векторы ζ) с неотрицательными координатами вида:
В соотношении (8) величина Iz есть агрегатный индекс себестоимости
, , где τ – произвольный параметр, возникающий при отыскании решений системы линейных уравнений (5). Тогда из соотношения (8) вытекает, что статистическая взаимосвязь между среднестатистическими индивидуальными индексами себестоимости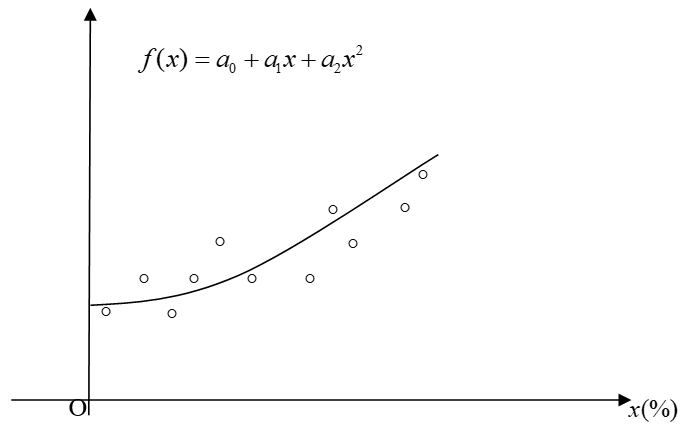
Рисунок 1 - Линия регрессии индекса себестоимости ¯iζ в зависимости от изменения среднестатистического темпа прироста затрат x(%):
° - данные наблюдений
Для иллюстрации предлагаемого подхода была рассмотрена выборка статистических данных объема N=42 о темпах прироста затрат x=ΔT(%)и изменения среднестатистических индексов себестоимости при деятельности 6-ти предприятий по переработке плодов и овощей за период с апреля по октябрь 2010г. При этом по каждому месяцу дополнительно рассматривались следующих выборки условных средних величин:
;
Статистическая обработка материала для анализа значимости квадратичной регрессии осуществлялась с помощью программного продукта «Анализ данных» в среде Excel c использованием среднемесячных значений вышеуказанных показателей по 6-ти предприятиям за указанный временной период. Для удобства исследования была введена вспомогательная переменная z=x2, исключающая коллинеарность x, z.
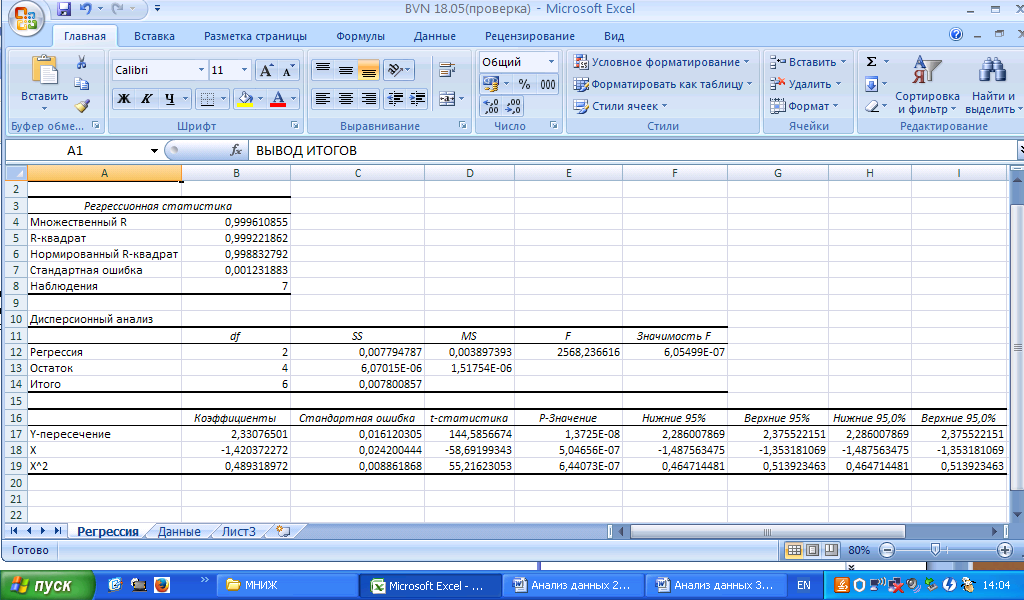
Рисунок 2 - Статистическая обработка материала
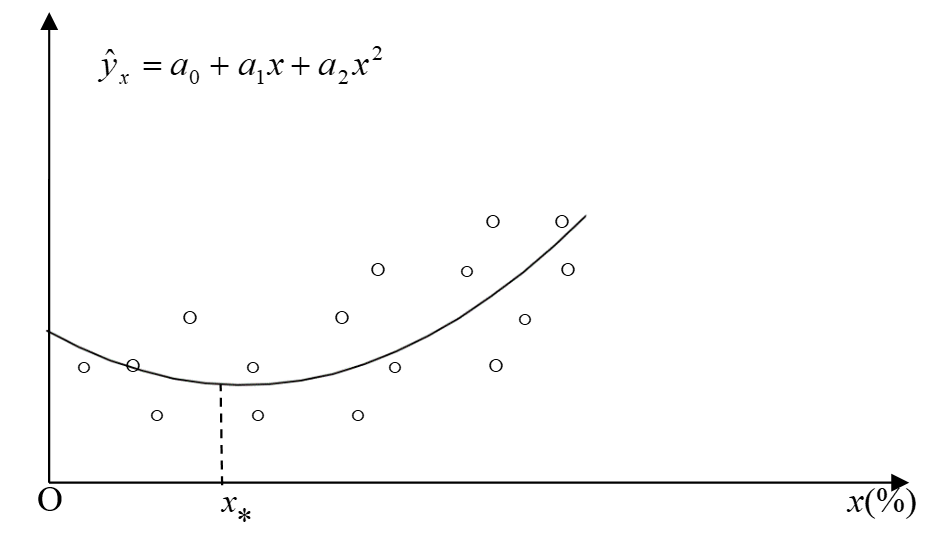
Рисунок 3 - Линия регрессии для описания корреляционной зависимости себестоимости продукции от прироста затрат на предприятиях по переработке плодов и овощей:
y(%) - индекс себестоимости продукции; x(%) - темп прироста затрат; ° - статистические данные наблюдений
Замечание
Отметим, что результат, описанный выше, полностью подтверждается результатами, полученными в работе
на основе обработки статистических данных для анализа взаимосвязи между средней себестоимостью промышленной продукции и изменением затрат на её производство, но не в относительном, а в абсолютном выражении значений указанных факторов. На основе исследования адекватности различных линейных и нелинейных моделей, рассмотренных в этой работе, наилучшую адекватность модели парной корреляции показала нелинейная квадратичная модель взаимосвязи факторов. При этом линия регрессии4. Заключение
1. На основе применения методов теоретической статистики и математического моделирования аналитически установлено наличие корреляционной связи между индексами себестоимости и темпом прироста в предположении прямой пропорциональной зависимости между среднестатистическими приростами самих факторов. Предлагаемый в работе аналитический подход для исследования нелинейного характера взаимосвязи изучаемых факторов является новым и ранее не применялся в подобных исследованиях.
2. Предлагаемый в работе новый аналитический подход позволяет построить математическую модель нелинейной взаимосвязи в форме квадратичной функции регрессии среднестатистического индекса себестоимости на темп прироста затрат в среднем по всему перечню наименований продукции. Предложенная на основе аналитических рассуждений математическая модель наиболее адекватно отражает реальную ситуацию, что подтверждается исследованиями других авторов.
3. Предлагаемый подход имеет перспективы использования в статистическом анализе результатов деятельности предприятий различной производственной направленности при оценке их конкурентоспособности на рынке товаров, планировании вопросов сбыта производимой продукции и, в частности, как показано в данной работе, на рынке продуктов переработки сельскохозяйственного сырья.
4. Предлагаемый новый подход имеет перспективы использованияв сфере таможенной деятельности в работе статистических центров обработки данных , для анализа статистической взаимосвязи между изменениями внешнеторгового товарооборота и изменением размеров таможенных пошлин по ряду наименований экспортируемой продукции.
