APPLYING EXCEL IN CRYPTOGRAPHY

Research article

Sdvizhkov O.A.

Matsnev N.P.

DOI:

https://doi.org/10.23670/IRJ.2020.97.7.013

Issue: № 7 (97), 2020

Published:

2020/07/17

PDF

ПРИМЕНЕНИЕ EXCEL В КРИПТОГРАФИИ

Научная статья

Сдвижков О. А.^1,*, Мацнев Н.П.²

¹Российский государственный университет туризма и сервиса, Черкизово, Россия;

²Технологический университет, Королев, Россия

* Корреспондирующий автор (oasdv[at]yandex.ru)

Аннотация

Создана библиотека пользовательских функций VBA Excel для автоматизации решений классических задач криптографии. В нее вошли пользовательские функции Excel для шифрования и дешифрования сообщений такими шифрами как Цезаря, лозунговым, Полибия, Тритемия, Белазо, Виженера, RSA, а также для кодирования и декодирования сообщений с помощью классических алгоритмов дискретной математики Хэмминга и Хаффмана. Приведены программные коды некоторых пользовательских функций. Применение пользовательских функций показано на задачах.

Ключевые слова: шифр, ключ, открытый ключ, алфавитное кодирование, самокорректирующийся код, префиксный код

APPLYING EXCEL IN CRYPTOGRAPHY

Research article

Sdvizhkov O.A.^1,*, Matsnev N.P.²

¹Russian State University of Tourism and Service, Cherkizovo, Russia;

²Technological University, Korolev, Russia

* Corresponding author (oasdv[at]yandex.ru)

Abstract

The VBA Excel library with user functions was made to automate the solutions to classic cryptography problems. It includes Excel user functions for messages encryption and decryption with such codes as Caesar, Slogan, Polybius, Tritemia, Belazo, Vigenere, RSA, also it contains functions for encoding and decoding messages with the classical discrete mathematics algorithms of Hamming and Huffman. The program codes for some user functions are provided. The application of custom functions is shown on tasks.

Keywords: code, key, public key, alphabetical coding, self-correcting code, prefix code

Введение

Одним из мощных средств автоматизации обработки данных в Excel является [3] применение пользовательских функций (user-defined functions), поддерживаемых на уровне встроенных средств, то есть имеющих диалоговые окна ввода данных и получения результатов.

Статья посвящена разработанным пользовательским функциям Excel, автоматически решающим задачи криптографии. Программные коды пользовательских функций приведены на сайте [8].

Пользовательские функции шифрования и дешифрования

Созданные пользовательские функции [8] и их назначения:

БЕЛАЗО – шифрует сообщение шифром Белазо;

БЕЛАЗООБР – дешифрует шифрограмму Белазо;

ВИЖЕНЕР – шифрует сообщение шифром Виженера;

ВИЖЕНЕРОБР – дешифрует шифрограмму Виженера;

ЛОЗУНГ – шифрует сообщение лозунговым шифром;

ЛОЗУНГОБР – дешифрует лозунговый шифр;

ПОЛИБИЙ – шифрует сообщение шифром Полибия;

ПОЛИБИЙОБР – дешифрует шифрограмму Полибия;

РСА – шифрует сообщение шифром RSA;

РСАОБР – дешифрует шифрограмму RSA;

ТРИТЕМИЙ – шифрует сообщение шифром Тритемия;

ТРИТЕМИЙОБР – дешифрует шифрограмму Тритемия;

ЦЕЗАРЬ – применяется шифр Цезаря.

В частности, код пользовательской функции ЦЕЗАРЬ и ее описания:

Function ЦЕЗАРЬ(Слово As String, Ключ As Integer) As String

Dim n As Integer, t As String, h As Integer

Dim p(0 To 31) As String

p(0) = "А": p(1) = "Б": p(2) = "В":p(3) = "Г": p(4) = "Д"

p(5) = "Е":p(6) = "Ж": p(7) = "З": p(8) = "И":p(9) = "Й"

p(10) = "К": p(11) = "Л":p(12) = "М": p(13) = "Н"

p(14) = "О":p(15) = "П": p(16) = "Р": p(17) = "С"

p(18) = "Т": p(19) = "У": p(20) = "Ф":p(21) = "Х"

p(22) = "Ц": p(23) = "Ч":p(24) = "Ш": p(25) = "Щ"

p(26) = "Ъ":p(27) = "Ы": p(28) = "Ь": p(29) = "Э"

p(30) = "Ю": p(31) = "Я":n = Len(Слово)

Dim q(0 To 31) As String

For i = 0 To 31

h = i + Ключ

If h >= 0 Then

h = h Mod 32

q(i) = p(h)

Else

q(i) = p(h + 32)

End If

t = ""

For i = 1 To n

For j = 0 To 31

If p(j) = Mid(Слово, i, 1) Then

t = t & q(j)

Exit For

End If

ЦЕЗАРЬ = t

End Function

Sub InstallFunc()

Application.MacroOptions Macro:="ЦЕЗАРЬ", Description:= _

"Шифрование (дешифрование) шифром Цезаря"

End Sub

Задача 1

Зашифровать слово ИНФОРМАЦИЯ шифром Цезаря при значении ключа равном 5.

Технология решения

Вызывается функция ЦЕЗАРЬ и вводятся данные (рис. 1).

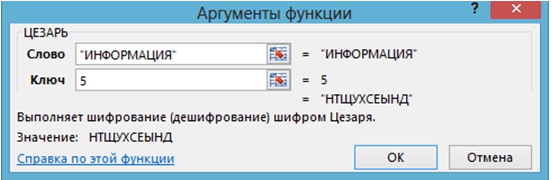
07-08-2020 11-20-35

Рис. 1 – Шифрование функцией ЦЕЗАРЬ

Пусть надо дешифровать НТЩУХСЕЫНД. Тогда снова применяется (рис. 2) функция ЦЕЗАРЬ, но при значении ключа равном -5:

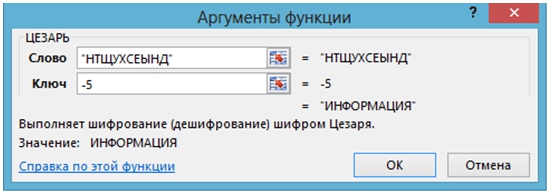
07-08-2020 11-20-52

Рис. 2 – Дешифрование функцией ЦЕЗАРЬ

Задача 2

Зашифровать лозунговым шифром слово ИНФОРМАЦИЯ, если лозунг (ключ) БИТ.

Технология решения

Вызывается функция ЛОЗУНГ и вводятся данные (рис. 3).

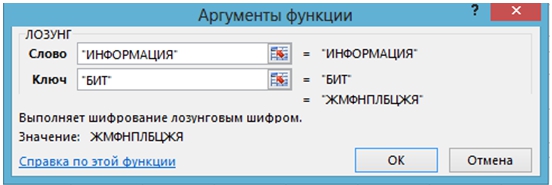
07-08-2020 11-21-04

Рис. 3 – Шифрование функцией ЛОЗУНГ

Задача 3

Дешифровать, полученную лозунговым шифром шифрограмму ЖМФНПЛБЦЖЯ, если лозунг БИТ.

Технология решения

Вызывается функция ЛОЗУНГОБР и вводятся данные (рис. 4).

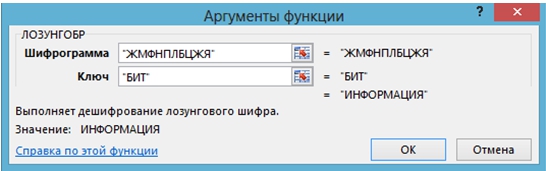
07-08-2020 11-24-50

Рис. 4 – Дешифрование функцией ЛОЗУНГОБР

Метод RSA выполняет шифрование с открытым ключом [1]. Для выбранной пары простых чисел P и Q, W= P·Q, шифрование выполняется по формуле:

С=М^R mod W,

М – порядковый номер шифруемой буквы в алфавите, С – порядковый помер буквы, на которую она заменяется, 1<R<L, НОД(R, L)=1, L = (P–1)(Q–1). Дешифрование выполняется по формуле:

М=С^S mod W,

в которой S удовлетворяет уравнению R·S mod L =1.

Метод RSA реализует пользовательская функция РСА, код которой имеет вид:

Function РСА(Модуль As Integer, Степень As Integer, _

Слово As String) As String

Dim n As Integer, m As Integer, h() As Variant, _

v As Integer, t As String

m = Len(Слово)

ReDim h(1 To m)

Dim p(1 To 32) As String

p(1) = "А": p(2) = "Б": p(3) = "В":p(4) = "Г": p(5) = "Д"

p(6) = "Е":p(7) = "Ж": p(8) = "З": p(9) = "И":p(10) = "Й"

p(11) = "К": p(12) = "Л":p(13) = "М": p(14) = "Н"

p(15) = "О":p(16) = "П": p(17) = "Р": p(18) = "С"

p(19) = "Т": p(20) = "У": p(21) = "Ф":p(22) = "Х"

p(23) = "Ц": p(24) = "Ч":p(25) = "Ш": p(26) = "Щ"

p(27) = "Ъ":p(28) = "Ы": p(29) = "Ь": p(30) = "Э"

p(31) = "Ю": p(32) = "Я"

For i = 1 To m

v = 1

For j = 1 To 32

If Mid(Слово, i, 1) = p(j) Then

For k = 1 To Степень

v = v * j Mod Модуль

h(i) = v

Exit For

End If

t = ""

For i = 1 To m

If h(i) < 10 Then

t = t & " 0" & Str(h(i))

Else

t = t & Str(h(i))

End If

РСА = t

End FunctionSub InstallFunc11()

Application.MacroOptions Macro:="РСА", Description:= _

"Возвращает RSA шифрограмму заданного слова"

End Sub

В программном коде РСА значения М^R mod W вычисляются с помощью цикла:

v = 1

For k = 1 To R

v = v * M Mod W

Такой подход, не требующий вычисления М^R, позволяет шифровать символы всего алфавита при достаточно больших значениях R.

Задача 4

Применяя пользовательскую функцию РСА, зашифруйте при P=5, Q=17, R=57 слово ЯЧЕЙКА.

Технология решения

Вызывается функция РСА и вводятся данные (рис. 5).

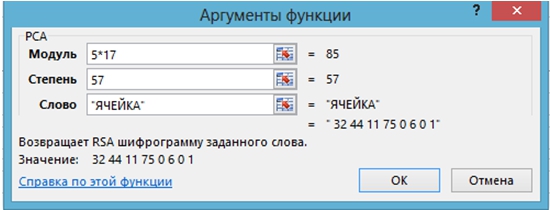
07-08-2020 11-28-50

Рис. 5 – Шифрование функцией РСА

Следует заметить, что получить результат с помощью встроенной функции ОСТАТ нельзя, в частности, формула =ОСТАТ(32^57; 85) не поддерживается.

Значение S возвращает пользовательская функция СТОБР [8].

Задача 5

Применяя функцию пользователя СТОБР, найти по данным задачи 4 значение S.

Скриншот решения:

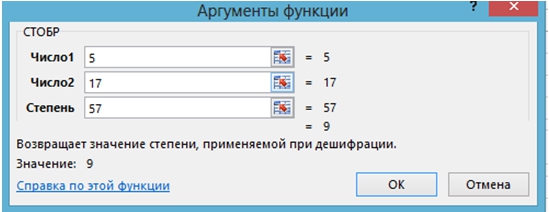
07-08-2020 11-29-04

Рис. 6 – Применение функции СТОБР

Дешифрование в методе RSA выполняет пользовательская функция РСАОБР:

Function РСАОБР(Модуль As Integer, Степень As Integer, _

Слово As String) As String

Dim n As Integer, m As Integer, h() As Variant, _

v As Integer, t As String

m = Len(Слово)

ReDim h(1 To m / 2)

Dim p(1 To 32) As String

p(1) = "А": p(2) = "Б": p(3) = "В":p(4) = "Г": p(5) = "Д"

p(6) = "Е": p(7) = "Ж": p(8) = "З": p(9) = "И":p(10) = "Й"

p(11) = "К": p(12) = "Л":p(13) = "М": p(14) = "Н"

p(15) = "О":p(16) = "П": p(17) = "Р": p(18) = "С"

p(19) = "Т": p(20) = "У": p(21) = "Ф":p(22) = "Х"

p(23) = "Ц": p(24) = "Ч":p(25) = "Ш": p(26) = "Щ"

p(27) = "Ъ":p(28) = "Ы": p(29) = "Ь": p(30) = "Э"

p(31) = "Ю": p(32) = "Я":t = ""

For i = 1 To m / 2

If Mid(Слово, 2 * i - 1, 1) = "0" Then

h(i) = Val(Mid(Слово, 2 * i, 1))

Else

h(i) = Val(Mid(Слово, 2 * i - 1, 2))

End If

v = 1

For k = 1 To Степень

v = v * h(i) Mod Модуль

t = t & p(Str(v))

РСАОБР = t

End Function

Sub InstallFunc13()

Application.MacroOptions Macro:="РСАОБР", _

Description:="Дешифрует шифрограмму RSA"

End Sub

В программном коде РСАОБР вычисления С^S mod W также проводятся с помощью цикла.

Задача 6

Применяя функцию пользователя РСАОБР, дешифруйте ключом (9, 5·17) шифрограмму 324411750601.

Скриншот решения:

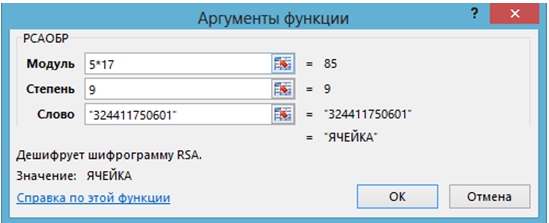
07-08-2020 11-31-39

Рис. 7 – Применение функции РСАОБР

Самокорректирующийся код Хэмминга Метод Хэмминга, кодирования двоичного сообщения α₁α₂… α_m самокорректирующимся кодом β₁β₂… β _n, изложен в [2, С. 245]. Код пользовательской функции, реализующей этот метод: Function ХЭММИНГ(Сообщение As String) As Variant Dim m As Integer, n As Integer, k As Integer, a() As Integer, _ b()As Variant, c As String m = Len(Сообщение) For i = 1 To 3 * m If 2 ^ m <= 2 ^ i / (i + 1) Then n = i Exit For End If Next k = n - m ReDim a(1 To m) As Integer For i = 1 To m a(i) = Mid(Сообщение, i, 1) Next ReDim b(1 To n) r = 0 For i = 1 To n If i = 2 ^ r Then r = r + 1 Else b(i) = a(i - r) End If Next r = 0 For i = 1 To n If i = 2 ^ r Then h = 0 For j = 2 ^ r + 1 To n q = Application.WorksheetFunction.Dec2Bin(j) If Mid(q, Len(q) - r, 1) = "1" Then h = (h + b(j)) Mod 2 End If Next b(i) = h r = r + 1 End If Next c = "" For i = 1 To n c = c & Str(b(i)) Next ХЭММИНГ = c End Function Sub InstallFunc() Application.MacroOptions Macro:="ХЭММИНГ", Description:= _ "Кодирует сообщение методом Хэмминга" End Sub Задача 7 Применяя пользовательскую функцию ХЭММИНГ, найти код Хэмминга сообщения 111001111. Скриншот решения: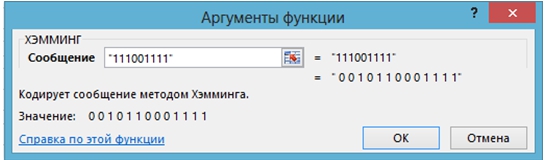

07-08-2020 11-32-21

Рис. 8 – Применение функции ХЭММИНГ к 111001111

Проверка значения β₄:

Декодирование кода Хэмминга, обнаруживающего не более одной ошибки, которое рассматривается в [2, С. 246], выполняет пользовательская функция ДЕХЭМ (код для краткости не приводится, см. [8]).

Задача 8

Применяя пользовательскую функцию ДЕХЭМ, декодируйте код Хэмминга задачи 7, если он получен с ошибкой и имеет вид 0010100001111.

Скриншот решения:

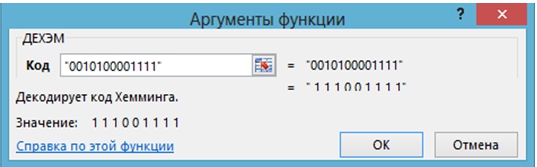
07-08-2020 11-36-21

Рис. 9 – Декодирование с исправлением ошибки

Алгоритм Хаффмана

Алгоритм Хаффмана, построения оптимального префиксного кода алфавита, символы которого принимаются с заданными вероятностями, изложен в [2, С. 236]. Он реализуется пользовательской функцией ХАФФМАН:

Function ХАФФМАН(Вероятности() As Variant) As Variant

Dim m As Integer, p() As Single, q() As String, _

h() As Integer, c() As Variant

m = UBound(Вероятности)

ReDim p(1 To m, 1 To m - 1)

ReDim q(1 To m, 1 To m - 1)

ReDim h(1 To m - 1)

ReDim c(1 To m)

For i = 1 To m

p(i, 1) = Вероятности(i)

For j = 2 To m - 1

d = 0

For i = 1 To m - j + 1

If i < m - j + 1 Then

p(i, j) = p(i, j - 1)

Else

p(i, j) = p(m - j + 1, j - 1) + p(m - j + 2, _

j - 1)

End If

For i = 1 To m - j

If p(i, j) < p(m - j + 1, j) Then

p(i, j) = p(m - j + 1, j)

h(j) = i

d = 1

For k = i + 1 To m - j + 1

p(k, j) = p(k - 1, j - 1)

End If

If d = 0 Then h(j) = m - j + 1

'Обратный ход:

q(1, m - 1) = "0"

q(2, m - 1) = "1"

For j = 1 To m - 2

For i = 1 To j

If p(i, m - j - 1) = p(i, m - j) And _

i < h(m - j) Then

q(i, m - j - 1) = q(i, m - j)

End If

If p(i, m - j - 1) = p(i + 1, m - j) And _

i >= h(m - j) Then

q(i, m - j - 1) = q(i + 1, m - j)

End If

q(j + 1, m - j - 1) = q(h(m - j), m - j) & " 0 "

q(j + 2, m - j - 1) = q(h(m - j), m - j) & " 1 "

For i = 1 To m

c(i) = q(i, 1)

ХАФФМАН = c

End Function

Sub InstallFunc()

Application.MacroOptions Macro:="ХАФФМАН", _

Description:="Возвращает по вероятностям " & _

"(частотам) код Хаффмана"

End Sub

Задача 9. Применяя пользовательскую функцию ХАФФМАН, найти оптимальный двоичный код алфавита, символы которого принимаются с вероятностями 0,6; 0,2; 0,1; 0,1.

Скриншот решения показан на рисунке 10, полученный префиксный код легко проверяется построением кодового дерева.

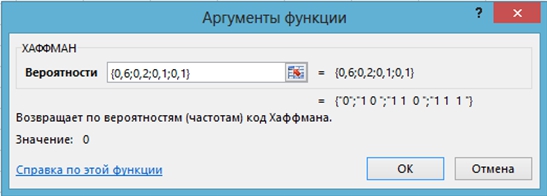
07-08-2020 11-37-55

Рис. 10 – Применение функции ХАФФМАН

Декодирование выполняется функцией ДЕХАФ [8].

Задача 10

Применяя пользовательскую функцию ДЕХАФ, декодируйте криптограмму Хаффмана 1000110111000110100010100, если A= {А, М, Т, Е, И, К}, C= {00, 10, 11, 011, 0100, 0101}.

Скриншот решения:

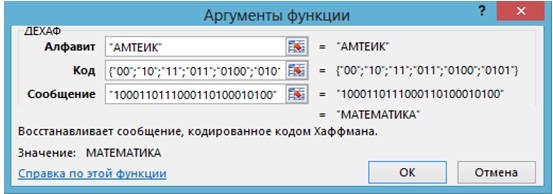
07-08-2020 11-38-11

Рис. 11 – Применение функции ДЕХАФ

Заключение

В самом доступном и популярном программном комплексе по обработке числовых данных, каким является Excel, созданы пользовательские функции VBA для решения задач криптографии.
Как видно из приведенных задач, применение пользовательских функций криптографии не вызывает трудностей.
Помещение программных кодов созданных пользовательских функций в одной книги Excel делает ее криптокалькулятором (рис. 12).

07-08-2020 11-42-24

Рис. 12 – Меню криптокалькулятора

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

Алферов А.П. Основы криптографии. Учебное пособие, 2-е изд, испр. и доп. / А.П. Алферов, А.Ю. Зубов и др. – М.: Гелиос АРВ, 2001. – 480 с.
Гаврилов Г.П. Задачи и упражнения по дискретной математике: Учебное пособие – 3-е изд., перераб. / Г.П. Гаврилов, А.А. Сапоженко – М.: ФИЗМАТЛИТ, 2003. – 416 с.
Гарнаев А.Ю. MS Excel 2002: Разработка приложений / А.Ю. Гарнаев – СПб. БХВ-Петербург, 2003. – 768 с.
Нечаев В.И. Элементы криптографии (Основы теории защиты информации): Учеб. пособие для ун-тов и пед. вузов / Под ред. В.А. Садовничего. –М.: Высш. шк.; 1999. – 109 с.
Осипян В.О. Криптография в задачах и упражнениях / В.О. Осипян, К.В. Осипян – М.: Гелиос АРВ, 2004. – 144 с.
Сдвижков О.А. Математика в Excel 2003 / О.А. Сдвижков – М.: СОЛОН-Пресс, 2005. – 192 с.
Сдвижков О.А. Excel-VBA. Словарь-справочник пользователя / О.А. Сдвижков – М.: Эксмо, 2008. – 224 с.
Сдвижков О.А. [Электронный ресурс] URL: http://oas.ucoz.com. . (дата обращения: 18.06.2020)
Смарт Н. Криптография / Н. Смарт – М.: Техносфера, 2005. – 528 с.
Яблонский С.В. Введение в дискретную математику: Учебное пособие для вузов / Под ред. В.А. Садовничего. – 4-е изд., стер. – М.: Высш. шк.; 2003. – 384 с.

Список литературы на английском языке / References in English

Alferov A. P. Osnovy kriptografii. Uchebnoe posobie, 2-e izd, ispr. i dop. [Basics of cryptography. Textbook, 2nd ed., ISPR. and extra] / A.P. Alferov, A.Ju. Zubov i dr. – M.: Gelios ARV, 2001. – 480 p. [in Russian]
Gavrilov G.P. Zadachi i uprazhnenija po diskretnoj matematike: Uchebnoe posobie – 3-e izd., pererab. [Problems and exercises in discrete mathematics: Textbook – 3rd ed., pererab] / G.P. Gavrilov, A.A. Sapozhenko – M.: FIZMATLIT, 2003. – 416 p. [in Russian]
Garnaev A.Ju. MS Excel 2002: Razrabotka prilozhenij [MS Excel 2002: application Development] / A.Ju. Garnaev – SPb. BHV-Peterburg, 2003. – 768 p. [in Russian]
Nechaev V.I. Jelementy kriptografii (Osnovy teorii zashhity informacii): Ucheb. posobie dlja un-tov i ped. vuzov [Elements of cryptography (Fundamentals of information security theory): Textbook for UN-tov and PED. universities] / ed. by V.A. Sadovnichego. –M.: Vyssh. shk.; 1999. – 109 p. [in Russian]
Osipjan V.O. Kriptografija v zadachah i uprazhnenijah [Cryptography in tasks and exercises] / V.O. Osipjan, K.V. Osipjan – M.: Gelios ARV, 2004. – 144 p. [in Russian]
Sdvizhkov O.A. Matematika v Excel 2003 [Math in Excel 2003] / O.A. Sdvizhkov – M.: SOLON-Press, 2005. – 192 p.
Sdvizhkov O.A. Excel-VBA. Slovar'-spravochnik pol'zovatelja [Excel-VBA. Dictionary-user reference] / O.A. Sdvizhkov – M.: Jeksmo, 2008. – 224 p. [in Russian]
Sdvizhkov O.A. [Electronic resource] URL: http://oas.ucoz.com. (accessed: 18.06.2020) [in Russian]
Smart N. Kriptografija [Cryptography] / N. Smart – M.: Tehnosfera, 2005. – 528 p. [in Russian]
Jablonskij S.V. Vvedenie v diskretnuju matematiku: Uchebnoe posobie dlja vuzov [Introduction to discrete mathematics: a textbook for universities] / ed. by. V.A. Sadovnichego. – 4-e izd., ster. – M.: Vyssh. shk.; 2003. – 384 p. [in Russian]