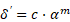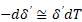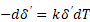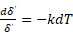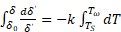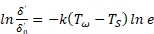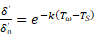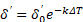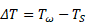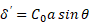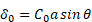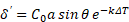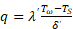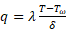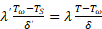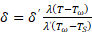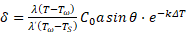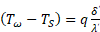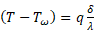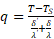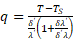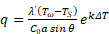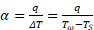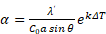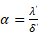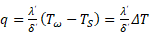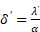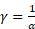ПЕРЕГРЕТЫЙ СЛОЙ ЖИДКОСТИ В РЕЖИМЕ ПУЗЫРЬКОВОГО КИПЕНИЯ

ПЕРЕГРЕТЫЙ СЛОЙ ЖИДКОСТИ В РЕЖИМЕ ПУЗЫРЬКОВОГО КИПЕНИЯ

Научная статья

Напольская Г. Ю.¹, Напольский В. П.²

₁Преподаватель ВЦ ВУНЦ ВВС «ВВА им. Проф. Н. Е. Жуковского и Ю. А. Гагарина» (г. Воронеж)

₂К.т.н., доцент, доцент кафедры ВУНЦ ВВС «ВВА им. Проф. Н. Е. Жуковского и Ю. А. Гагарина» (г. Воронеж)

Аннотация

Проведен температурный анализ толщины перегретого слоя жидкости и переохлажденного слоя твердого тела или расплава и предложены математические модели теплового потока и коэффициента теплоотдачи. Результаты согласуются с эмпирическими значениями, полученными ранее.

In the article the temperature analysis of the overheated layer thickness of a liquid and the overcooled layer of a firm body or melt is carried out and on the basis of the received results mathematical models of a thermal stream and factor of the heat transfer are offered. The received results are co-ordinated with the empirical values received earlier.

Ключевые слова: пузырьковое кипение, коэффициент теплоотдачи, капиллярная постоянная, перегретый слой.

Keywords: nucleate boiling, the heat transfer coefficient, the capillary constant, super-heated layer.  

Исследования характера распределения температуры на границе раздела двух фаз (твёрдое тело - жидкость или расплав металла или сплава - жидкость) показывают [1 – 2], что в указанной области существует перегретый пристенный слой жидкости и переохлаждённый слой твёрдого тела или расплава. Эти два слоя и определяют градиент температуры в зоне соприкосновения двух фаз, а, следовательно, плотность теплового потока и коэффициента теплоотдачи.

Маркусом и Дропкиным была установлена эмпирическая взаимосвязь между толщиной перегретого слоя в жидкости и коэффициентом теплоотдачи α при ядерном кипении жидкости, которая имеет следующий вид [2]:

                                                             (1)

где с и  m –константы.

Из указанной работы следует, что при тепловых потоках 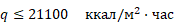 величина m = – 1, а при тепловых потоках  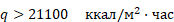m = – .  Обработка данных [2] методом наименьших квадратов показала, что  m = – 0,49.

В результате анализа полученных результатов исследователи приходят к выводу, что «экстраполированная толщина перегретого слоя»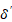 зависит от коэффициента теплоотдачи, описываемого уравнением (1).

Увеличение температуры жидкой фазы в пристенном слое на величину  приводит к изменению толщины перегретого слоя на величину 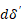. В этом случае справедливо:

                                                         ,                                           (2)

где 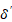 – толщина пристенного перегретого слоя жидкости.

Если ввести коэффициент пропорциональности 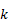, то можно записать:

.                                           (3)

Знак минус в уравнении (3) означает то, что с увеличением температуры величина перегретого слоя жидкости будет уменьшаться.

Разделив переменные в уравнении (3), получим

       .                                                (4)

Проинтегрируем уравнение (4):

.                                            (5)

В результате интегрирования уравнения (5) получим:

,                                        (6)

где 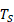 – температура кипения жидкости,  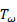– температура твердого тела или расплава,  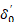- начальная толщина перегретого слоя жидкости.

Потенцируя выражение (6), придём к результату:

.                                               (7)

Из выражения (7) следует, что

, (8)

где  – температурный напор.

Толщина жидкой плёнки определяется уравнением [3]:

,                                                (9)

где 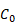 – постоянная величина, определяемая по опытным данным, a - капиллярная постоянная,  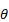-  краевой угол смачивания.

Процессы, определяющие теплообмен при пузырьковом кипении, происходят в такой области вблизи твердой стенки, где при однофазной турбулентной конвекции гидродинамические возмущения не ощущаются [4]. Путем теплопроводности будет осуществляться трансляция тепла от твёрдого тела (нагревателя) к жидкости. Начальная толщина перегретого слоя жидкости определяться выражением [5]:

,                                                (10)

Используя выражение (10), формулу (8) можно записать:

,                                             (11)

Формула (11) определяет толщину перегретого слоя жидкости при различных её перегревах.

На границе раздела твёрдое тело - жидкость или расплав - жидкость плотность теплового потока определим уравнением Фурье, которое с использованием перегретого слоя жидкости будет иметь вид:

.                                                (12)

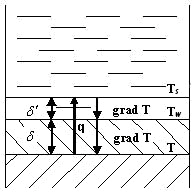
Через переохлаждённый слой твёрдой поверхности или расплава, с которым соприкасается кипящая жидкость (рис. 1), величина q определяется:

                                                                                         (13)

Рисунок 1 – Процесс трансляции тепла на границе раздела фаз

На основании уравнений (12) и (13) можно записать:

                                       (14)

Тогда величина переохлаждённого слоя твёрдого тела или расплава будет определяться:

.                                         (15)

Используя уравнение (11), выражение (15) представим в виде:

,                                (16)

которое и будет определять толщину переохлаждённого слоя твёрдого тела или расплава.

С другой стороны, из уравнений (11) и (12) следует, что

,                                           (17)

.                                           (18)

Сложив левые и правые части уравнений (17) и (18), а полученный результат решив относительно плотности теплового потока , получим:

,                                             (19)

или

.                                         (20)

Подставив выражения (11) и (16) в уравнение (20), после несложных преобразований, получим:

.                                         (21)

Уравнение (21) определяет величину плотности теплового потока на границе раздела твёрдое тело - жидкость или расплав - жидкость.

Так как коэффициент теплоотдачи определяется выражением:

,

то с использованием выражения (20) коэффициент теплоотдачи можно определить:

.                                               (22)

Таким образом, из уравнений (21) и (22) следует, что с увеличением температурного напора 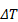 плотность теплового потока и коэффициент теплоотдачи будут возрастать по экспоненциальной зависимости. В то же время q и α зависят от теплопроводности  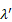жидкости, её капиллярной постоянной α и краевого угла смачивания θ.

Наличие перегретого и переохлаждённых слоёв на границе раздела фаз обеспечивают трансляцию тепла в направлении противоположном градиенту температуры.

Следовательно,

.                                                       (23)

Таким образом, коэффициент теплоотдачи прямо пропорционален теплопроводности 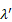 жидкости и обратно пропорционален толщине  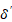перегретого слоя жидкости.

Очевидно, что величину теплового потока можно представить:

.                                        (24)

Из уравнения (23) следует, что

.                                                       (25)

Из уравнения (25) видно, что возможна обратная задача – определение толщины перегретого слоя жидкости по коэффициенту теплопроводности и коэффициенту теплоотдачи α.

Запишем уравнение (25) в следующем виде:

,                                                     (26)

где .

Сравнивая выражения (26) и (1) видно, что они становятся эквивалентными по физическому смыслу лишь при m = – 1, при условии, что постоянная с в уравнении (1) имеет размерность коэффициента теплопроводности. При m = –   расхождение полное.

Таким образом, выражение (25) позволяет оценить величину перегретого пристенного слоя жидкости по коэффициенту теплопроводности и коэффициенту теплоотдачи во всём режиме ядерного кипения жидкости при различных поверхностных эффектах, которые в значительной степени влияют на процесс теплообмена, а, следовательно, и на величину перегретого слоя жидкости.

Список литературы / References

1. Cooper, M. G. Transient local heat flux in nucleate boiling/ Cooper M. G., Lloyd A. P. // Proceedings of the Third International Heat Transfer Conference. Chicago 1966. P. 193—203.
2. Маркус Б.Д. Дропкин Д. Экспериментальное исследование температурных профилей в перегретом пограничном слое над горизонтальной поверхностью при пузырьковом кипении в большом объеме. / Б.Д Маркус, Д. Дропкин // Тр.амер. о-ва инж.-мех. Сер.С, 1965,87,№3, с.14-34.
3. Марков, И.И. О толщине жидкой плёнки на горизонтальной подложке./ И.И. Марков, М.В. Батурин // Циклы природы и общества/Материалы V международной конференции.Ч.2. Ставрополь, 1997. – С.94-97.
4. Лабунцов, Д.А. Физические основы энергетики. Избранные статьи по теплообмену, гидродинамике и термодинамике. М.: Издательство МЭИ, 2000.
5. Лабунцов, Д. А. Приближённая теория теплообмена при развитом пузырьковом кипении //Известия АН СССР. Энергетика и транспорт. – –  №1. – С. 58 – 71.