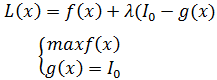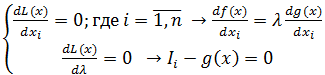NEW IN THE THEORY OF PRODUCTION FUNCTIONS
Некрестьянова Ю.Н.
Аспирант, Государственный университет управления
НОВОЕ В ТЕОРИИ ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ
Аннотация
В статье решена задача нахождения точки рыночного равновесия (где доход от производственной функции равен издержкам производства, при этом равны и max приросты их изменения) тремя различными способами: градиентным методом; методом Лагранжа; методом оптимальных весовых коэффициентов (метод, предложенный автором статьи). Тождественность результата – это доказательство достоверности метода оптимальных весовых коэффициентов.
Ключевые слова: производственная функция, принцип наименьшего действия, оптимальные весовые коэффициенты.
Nekrestianova U.N.
Postgraduate student, State University of management
NEW IN THE THEORY OF PRODUCTION FUNCTIONS
Abstract
The article solves the problem of finding the point of market equilibrium (where the income from the production function is equal to cost of production, equal and max gain their modifications) in three different ways: gradient method; the method of Lagrange; by the method of optimal weighting coefficients (method proposed by the author of the article). The identity of the result is proof of the validity of the method of optimal weighting coefficients.
Keywords: production function, the principle of least action, optimal weighting coefficients.
Теория производственных функций давно и широко используется в экономической науке для решения задач как макро, так и микро экономики (например, в теории фирмы). Преподавание теории производственных функций обычно осуществляется на примере функций двух переменных (например, [1]), так как в этом случае легко использовать геометрические иллюстрации и доказательства. В качестве типичной производственной функции двух переменных используется известная функция Кобба-Дугласа в виде:
Чаще ее представляют в виде:
Параметры a0, a1, a2 обычно определяются путем обработки статистической информации, то есть апостериори (после опыта), что плохо для прогнозов. Производственная функция (2) – это функция дохода от макроэкономики (отрасли, региона, страны в целом). Под переменными (параметрами производства) K и L понимаются объемы привлекаемых в экономику за рассматриваемый временной интервал «T» капиталов (K) и затрат средств на трудовые ресурсы (L), функция издержек при этом имеет вид:
Где b1, b2 – коэффициенты инфляции (средние) за период «Т».
Сразу же отметим важный факт, что g(x) является однородной функцией со степенью однородности единица. Это следует из того, что
Из теории известно, что всегда существует точка так называемого рыночного равновесия и в этой точке x*=(x1*,x2*) значения дохода f(x*) и издержек g(x*) равны, то есть
Из равенств (5) очевидно следует, что
То есть по определению однородной функции f(x) – однородна со степенью однородности единица. Таким образом f(x) и g(x) всегда будут иметь одинаковую степень однородности. Так как из вида (2) производственной функции f(x) следует, что
то получаем требование:
Таким образом, параметры a1 и a2 можно рассматривать как весовые коэффициенты факторов производства K и L. Это очень важный результат, который при достаточно достоверной и объемной статистической выборке должен подтверждаться на практике. И действительно, в работ [3] это подтверждение есть. Для макроэкономической производственный функции Кобба-Дугласа в [3] для экономики США приведены значения параметров и , полученные разными авторами для различных базовых временных промежутков. При этом особо подчеркивается, что авторами априори не предполагалось, что (a1+a2)=1. В таблице 1 представлены лишь два из представленных в работе [3] результата полученных известными в мире экономистами (Дугласом и Солоу).
Таблица 1 - Значения параметров a1 и a2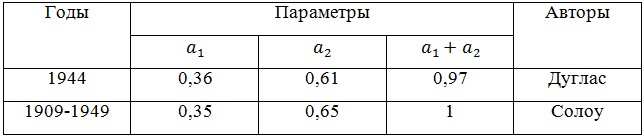
Из [3] и таблицы 1 следует, что a1 ≠ a2 и что a1 и a2 отстоят от 1/2 на одном расстоянии, то есть ā – a1 ≈ a2 - ā. При этом (a1 + a2) = 1. Однако главный результат получен в [2], где показано, что существуют оптимальные значения весовых коэффициентов ![]() по критерию принципа наименьшего действия. При этом не только всегда
по критерию принципа наименьшего действия. При этом не только всегда ![]() , но и существуют конкретные оптимальные числовые значения весовых коэффициентов
, но и существуют конкретные оптимальные числовые значения весовых коэффициентов ![]() , которые являются функциями их числа n. В случае n = 2 получаются оптимальные значения a1 = 0,382 b a2 = 0,618. Это известное «золотое сечение» единицы на две оптимальные части (при этом 0,5 – 0,382 = 0,618 – 0,5 = 0,118). Это подтверждается, учитывая статистическую погрешность, и таблица 1 (особенно результат Солоу). В работе [2] получена формула расчета оптимальных значений весовых коэффициентов ai в случае произвольного их числа n в виде:
, которые являются функциями их числа n. В случае n = 2 получаются оптимальные значения a1 = 0,382 b a2 = 0,618. Это известное «золотое сечение» единицы на две оптимальные части (при этом 0,5 – 0,382 = 0,618 – 0,5 = 0,118). Это подтверждается, учитывая статистическую погрешность, и таблица 1 (особенно результат Солоу). В работе [2] получена формула расчета оптимальных значений весовых коэффициентов ai в случае произвольного их числа n в виде:
Здесь p > 0 – максимальный действительный корень полинома вида: ![]() . Таким образом для производственной функции Кобба-Дугласа получаем оптимальный вариант
. Таким образом для производственной функции Кобба-Дугласа получаем оптимальный вариант ![]() ;
; ![]() ; a0 = const. То есть
; a0 = const. То есть
Для многофакторных производственных функций известна производственная функция Ричарда Стоуна, следующего вида:
где ![]() . Здесь также оптимальный вариант будет при ai определяемых по формулам (8), причем
. Здесь также оптимальный вариант будет при ai определяемых по формулам (8), причем ![]() . Таким образом доказано, что в теории производственных функций типа Ричарда Стоуна (производственная функция Кобба-Дугласа здесь частный случай при n = 2) параметры ai действительно являются весовыми коэффициентами факторов производства
. Таким образом доказано, что в теории производственных функций типа Ричарда Стоуна (производственная функция Кобба-Дугласа здесь частный случай при n = 2) параметры ai действительно являются весовыми коэффициентами факторов производства ![]() . Более того, получена формула (8) для расчета их оптимальных значений при каждом n.
. Более того, получена формула (8) для расчета их оптимальных значений при каждом n.
Для определения величины константы ![]() нужно воспользоваться точкой x* рыночного равновесия, где f(x*) = g(x*). В общем случае (n - мерном) функция издержек
нужно воспользоваться точкой x* рыночного равновесия, где f(x*) = g(x*). В общем случае (n - мерном) функция издержек
Здесь bi - коэффициент инфляции. Тогда из равенства ![]() , получаем
, получаем
Для определения координат точки x* рыночного равновесия можно использовать результат работы [2]. А именно из g(x*) = I0 имеем:
Из (13) получаем равенства
Таким образом, координаты xi* находятся без решения задачи оптимизации производственной функции. Но при этом используется оптимизация по принципу наименьшего действия. Для доказательства правильности определения величин xi* найдем их из решения задачи max прибыли
Покажем, что точкой max φ(x) будет та же самая точка рыночного равновесия x*, где f(x*) = g(x*) = I0. Для этого вычислим дифференциал φ(x) и приравняем его нулю. Из (15) получаем
Из (16) следует, что df(x) = dg(x), то есть
Так как – мерные поверхности
касаются в точке x* = (x1*,…, xn*), то при величине g(x*) = I0 и величина f(x*) = I0. Тогда из (17) имеем
То есть действительно
Равенства (20) и (14) являются тождественными. При этом (14) получены через принцип наименьшего действия, а (19) при решении задачи максимизации прибыли φ(x). Таким образом, доказана справедливость равенств (14) и подхода (способа) их получения.
Получим теперь уравнения (14) еще одним способом: методом Лагранжа. Для этого решим задачу на условный экстремум (max) для производственной функции вида ![]() при бюджетном ограничении
при бюджетном ограничении ![]() . В рассматриваемой задаче функция Лагранжа будет иметь вид:
. В рассматриваемой задаче функция Лагранжа будет иметь вид:
Как известно, решение находится путем решения системы уравнений (нахождения величин xi) вида:
Так как ![]() и
и ![]() , то из (22) имеем уравнения:
, то из (22) имеем уравнения:
Умножая уравнения (23) на xi и суммируя по ![]() получаем:
получаем:
Так как из единичной степени однородности f(x) и g(x) следует, что ![]() и справедливо равенство
и справедливо равенство ![]() , то из (24) получаем, что:
, то из (24) получаем, что:
Подставляя это значение λ в уравнения (23), получаем равенства:
то есть
Здесь ai - весовые коэффициенты факторов производства xi, которые находятся по формулам (8).
Уравнения (27) и (14) являются тождественными. Таким образом, решение (14) получено тремя различными методами, что доказывает и его достоверность и достоверность всех трех методов решения. В итоге получено еще одно доказательство оптимального по принципу наименьшего действия разложения любой const = I0 на n частей в виде: ![]() , где ai - весовые коэффициенты (т.е.
, где ai - весовые коэффициенты (т.е. ![]() ) определяемые формулами (8).
) определяемые формулами (8).
Заметим, что в более общем случае, когда функция издержек g(x) имеет степень однородности величиной p (то есть g(x) не будет линейной формой, а будет, например, квадратичной формой вида ![]() , то есть однородной степени p = 2), функция дохода f(x) в виде (10) также будет иметь степень однородности
, то есть однородной степени p = 2), функция дохода f(x) в виде (10) также будет иметь степень однородности
Преобразуя (21) к виду ![]() , где γi – весовые коэффициенты (определяемые по формуле (8)) факторов производства Xi. При этом параметры ai также всегда вычисляются через γi и p в виде ai = γi p.
, где γi – весовые коэффициенты (определяемые по формуле (8)) факторов производства Xi. При этом параметры ai также всегда вычисляются через γi и p в виде ai = γi p.
Кроме того, метод оптимизации через оптимальные весовые коэффициенты применим к зависимым переменным (либо функциям)! В нашем случае ![]() , где zi = fi(xi) = φ(xi,ai) это зависимые через параметры (весовые коэффициенты) переменные - функции. Например, если в виде zi(xi,ai) = cixiai (вектор параметров a = (a1,…,an)) рассмотреть локальные критерии оптимальности процесса производства, которые очевидно всегда зависимы, то интегральный критерий может быть выражен, например, их средним геометрическим
, где zi = fi(xi) = φ(xi,ai) это зависимые через параметры (весовые коэффициенты) переменные - функции. Например, если в виде zi(xi,ai) = cixiai (вектор параметров a = (a1,…,an)) рассмотреть локальные критерии оптимальности процесса производства, которые очевидно всегда зависимы, то интегральный критерий может быть выражен, например, их средним геометрическим ![]() (либо в виде lnf(x,a)=Φ(x,a), что при дифференцировании обеспечит безразмерность).
(либо в виде lnf(x,a)=Φ(x,a), что при дифференцировании обеспечит безразмерность).
В заключение, необходимо отметить, что предложенный в статье метод оптимальных весовых коэффициентов позволяет легко решать целый ряд задач экономики (например, задача оптимального распределения ресурсов бюджета по статьям расходов и т.п.).
Литература
- Замков О.О., Толстопятенко А.В., Черемых Ю.Н. Математические методы в экономике. – М.: Дело и сервис, 2001.
- Некрестьянова Ю.Н. Оптимизация значений весовых коэффициентов критериев эффективности инвестиционного проекта / Ю.Н. Некрестьянова // Эффективные механизмы инновационно-технологического развития современного общества : материалы IX Всероссийской (с международным участием) научно-практической конференции, г. Сочи, 23-24 мая 2013 г. / НОУ ВПО СИЭИТ – Сочи: «Стерх ГРУП», 2013. – с. 60 – 62. – 0,15 п.л.
- Терехов Л.Л. Производственные функции. – М.: Статистика, 1974.
References
- Zamkov O. O., Tolstopyatenko A.V., Jeremih Yu. Mathematical methods in Economics. – M.: Delo I SERVIS, 2001.
- Nekrestyanova U. N. Optimization of the weighting factors of criteria of efficiency of the investment project / U. N. Nekrestyanova // Effective mechanisms of innovative-technological development of modern society : materials of the IX all-Russian (with international participation) scientific-practical conference, Sochi, 23-24 may 2013 / NOU VPO SIIT – Sochi: "Siberian crane GROUP, 2013. – p. 60 – 62.
- Terekhov, L. L. the Production function. – M.: Statistics, 1974.