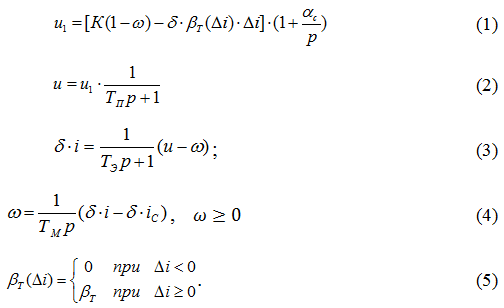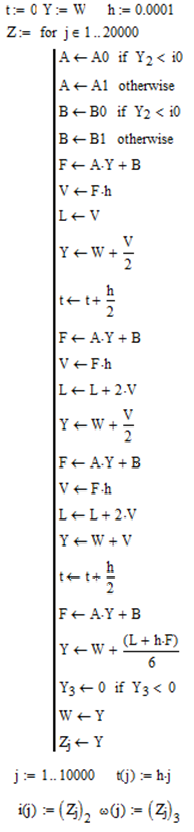SIMULATION OF DC ELECTRIC DRIVE WITH A VARIABLE STRUCTURE IN MATHCAD
Сташинов Ю.П.
Кандидат технических наук, Шахтинский институт (филиал) Южно-Российского государственного политехнического университета (НПИ) имени М.И. Платова
МОДЕЛИРОВАНИЕ ЭЛЕКТРОПРИВОДА ПОСТОЯННОГО ТОКА С ПЕРЕМЕННОЙ СТРУКТУРОЙ В СРЕДЕ MATHCAD
Аннотация
Приведена математическая модель электропривода постоянного тока с переменной структурой в виде структурной схемы и системы дифференциальных уравнений в нормальной векторной форме dY/dt=A·Y+B, где матрица А и вектор В дискретно изменяются при достижении одной из переменных состояния (током якорной цепи) уровня отсечки. Предложен программный модуль в MathCAD для численного решения указанной системы уравнений, с применением которого выполнено моделирование процесса пуска электропривода.
Ключевые слова: моделирование, электропривод, переменная структура, маткад
Stashinov Yu.P.
Candidate of Technical Sciences, Shakhty Institute (Branch) of South-Russian State Polytechnic University (Novocherkassk Polytechnic Institute) by M.I. Platov
SIMULATION OF DC ELECTRIC DRIVE WITH A VARIABLE STRUCTURE IN MATHCAD
Abstract
The mathematical model of the dc electric drive with a variable structure is represented by the structural diagram and the system of differential equations of the normal vector form dY/dt=A·Y+B, where matrix and vector B are discretely changing, when one of the state variables (the armature current) reaches the cut-off level. The program module in MathCAD for numeric solution of the mentioned system of equations was suggested and used for simulation of the process of drive start up.
Keywords: simulation, electric drive, variable structure, MathCAD
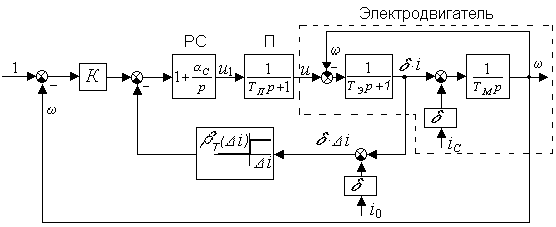
В ряде электроприводов постоянного тока получила применение система управления с ПИ-регулятором скорости и жёсткой отрицательной обратной связью по току с отсечкой. Система обеспечивает получение жёсткой механической характеристики электропривода в зоне рабочих нагрузок с защитой от перегрузок, в том числе в режиме стопорения. На рис. 1 приведена структурная схема такой системы с записью переменных состояния в относительных единицах [1]. За базовые величины для тока i, угловой скорости ω и напряжения u приняты, соответственно, номинальный ток электродвигателя Iн, заданное значение угловой скорости Ω0 и величина ЭДС вращения якоря электродвигателя Ea=Cв·Ω0 при угловой скорости Ω0.
Рис. 1 - Структурная схема системы управления электропривода постоянного тока с токовой отсечкой
На схеме приняты следующие обозначения:
K, βT – коэффициенты усиления контуров угловой скорости и тока;
αc – коэффициент интегральной составляющей регулятора угловой скорости (РС);
TП, ТЭ – электромагнитные постоянные времени преобразователя П (управляемого выпрямителя) и якорной цепи электродвигателя;
ТМ – электромеханическая постоянная времени привода;
δ=Iн·Ra / Cв· Ω0 – статизм разомкнутой системы управления, равный относительному (в долях заданного значения Ω0) снижению угловой скорости Ω при увеличении тока якоря от нулевого значения до номинального Iн, где Ra – сопротивление якорной цепи электродвигателя;
ic – статическая величина тока якорной цепи двигателя;
i0 – величина тока отсечки; Δi = i – i0.
Принципиальной особенностью рассматриваемой системы является то, что её структура изменяется при переходе одной из переменных состояния (тока якорной цепи i) через пороговое значение, равное величине тока отсечки i0. Отрицательная обратная связь по току вступает в действие при пуске электропривода, а также при набросе нагрузки только при выполнении условия: I > i0.
Приведенной на рис.1 структурной схеме соответствует следующая система интегро-дифференциальных уравнений в операторной форме записи:
Дифференцируя (1) с учётом соотношений (3, 4), запишем систему уравнений (1–5) в нормальной форме Коши:
где Y – вектор переменных состояния (Y0 = u1, Y1 = u, Y2 = i, Y3 = ω);
A – матрица размером 4х4;
B – вектор воздействий.
Введём также вектор начальных условий W = (K 0 0 0)T.
Встроенные средства MathCAD не предусмотрены для решения систем дифференциальных уравнений, описывающих поведение динамических систем, структура или параметры которых дискретно изменяются при достижении переменными состояния некоторых пороговых уровней. В связи с этим предлагается программный модуль (рис. 2) для исследования поведения рассматриваемой системы, реализующий алгоритм Рунге-Кутты 4-го порядка. Модуль позволяет на каждом шаге численного интегрирования системы дифференциальных уравнений отслеживать текущие значения переменных состояния и по результатам сравнения их с пороговыми значениями принимать соответствующие выражения для матрицы A и вектора воздействий В. В частности в исследуемой системе отслеживаются величины тока якорной цепи Y2 и угловой скорости Y3.
Рис. 2 - Программный модуль решения системы уравнений
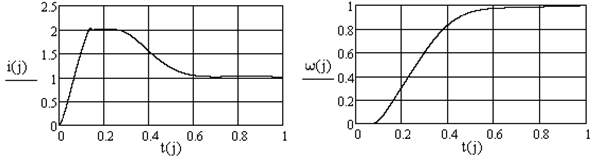
С использованием программного модуля на рис. 3 в качестве примера приведены результаты моделирования процесса пуска электропривода при номинальной нагрузке (iс = 1) и следующих численных значениях параметров: ТП = 0,01с; ТЭ = 0,05с; ТМ = 0,1с; δ = 0,3;
K = 0,25; αс = 20; βТ = 50; i0 = 2.
Рис. 3 - Зависимости тока якорной цепи и угловой скорости от времени при пуске электропривода
Рассматриваемый в данной работе подход и предложенный программный модуль с необходимой корректировкой можно использовать для исследования поведения широкого класса динамических систем с переменными структурой или параметрами, поведение которых во времени описывается системой дифференциальных уравнений в нормальной форме Коши относительно переменных состояния.
Литература
- Сташинов Ю.П. Курс лекций по системам управления электроприводов [Электронный ресурс] URL: http://twirpx.com/file/858316/ (дата обращения 15.03.2015).
References
- Stashinov Ju.P. Kurs lekcij po sistemam upravlenija jelektroprivodov. [Jelektronnyj resurs] URL: http://twirpx.com/file/85816/ (data obrashhenija 15.03.2015).