THE OPERATOR ANALOGUE OF INEQUALITY OF CAUCHY-BUNYAKOVSKIY
Рузимбой М.М.1, Садокат Б.А.2, Абдикаримов Ф.Б.3, Юсупов Б.Б.4
1Кандидатов наук, заведующие кафедрой теории функции, Ургенчского Государственного университета; 2преподаватель кафедры теории функции, Ургенчского Государственного университета; 3магистр, Физико-математический факультет, Ургенчского Государственного университета; 4студент, Физико-математический факультет, Ургенчского Государственного университета
ОПЕРАТОР АНАЛОГА НЕРАВЕНСТВА КОШИ — БУНЯКОВСИЙ
Аннотация
В статье рассмотрены определения левых и правых абсолютных значений оператора и их свойства. Получен операторный аналог неравенства Коши — Буняковского.
Ключевые слова: неравенство оператор, левое и правое абсолютное значение, аналог, неравенство Коши — Буняковского, лемма.
Ruzimboy M.M.1, Sadoqat B.A.2, Abdikarimov F.B.3, Yusupov B.B.4
1PhDs , chairs of department of theory of functions, Urgench State university; 2Assistant-teacher, department of theory of functions, Urgench State university; 3Master, Physical and mathematical faculty, Urgench State university; 4Student, Physical and mathematical faculty, Urgench State university,
THE OPERATOR ANALOGUE OF INEQUALITY OF CAUCHY-BUNYAKOVSKIY
Abstract
The article describes the determination of the left and right of the absolute values of the operator and their properties. The operator analogue of the inequality of Cauchy – Bunyakovski is obtained.
Keywords: inequality the operator, the left and right absolute value, analogue, inequality of Cauchy — Bunyakovsky, lemma.
Определение 1 (см. [7]).
Пусть H – Гильбертово пространство. Оператор ![]() называется положительным, если
называется положительным, если ![]() для всех
для всех ![]() . Мы пишем
. Мы пишем ![]() , если A положителен, и
, если A положителен, и ![]() .
.
Теорема(см. [7]).
Пусть ![]() . Тогда существует единственный оператор
. Тогда существует единственный оператор ![]() . Боле того, B коммутирует с любым ограниченным оператором, коммутирующим с A.
. Боле того, B коммутирует с любым ограниченным оператором, коммутирующим с A.
Определение 2.
Пусть ![]() . Тогда
. Тогда ![]() - правый (
- правый (![]() - левый) называется правая (левая) абсолютная значения оператора A.
- левый) называется правая (левая) абсолютная значения оператора A.
Правая абсолютная значения оператор имеют следующая свойства:
1) ![]()
2) ![]()
В общем случае не верны
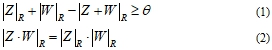
Для неравенство треугольники приведем пример Э.Нельсона. Пусть
![]()
Не верны.
Пусть ![]() . Очевидно, что для свойства абсолютная значения оператора верны для левая абсолютная значения оператора.
. Очевидно, что для свойства абсолютная значения оператора верны для левая абсолютная значения оператора.
Для каких пространств верны неравенство (1) и равенство (2). Нетрудно доказывается следующая теорема.
Теорема 2.
Для пространств действительных чисел, комплексных чисел, квартернион, октанион и диагональных операторов справедливо неравенство (1) и равенство (2).
Операторный аналоги неравенство Коши Буняковский когда обобщение неравенство (2).
Теорема 3.
Для ![]() и верны следующие неравенство:
и верны следующие неравенство:
![]()
(Очевидно, это неравенство верно левый абсолютная значения оператора).
Для доказательства теоремы 3 мы используем следующему лемму.
Лемма:
Для ![]() верный следующие неравенство:
верный следующие неравенство:
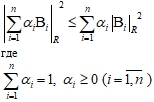
Доказательство.
Пусть ![]() тогда легко доказать, что
тогда легко доказать, что
![]() (3)
(3)
Из неравенства (3) находим, что,
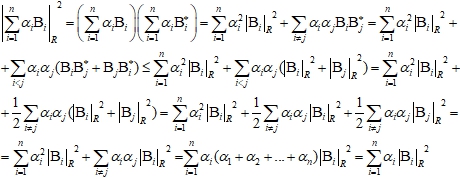
Лемма доказана.
Доказательство теоремой 3.
Рассмотрим следующие случае:
1-случай. Для ![]() . Тогда очевидно будить равенства.
. Тогда очевидно будить равенства.
2-случай. Для ![]() . Для
. Для 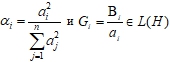
операторы выполняет условие леммы.
Тогда выполняет следующие неравенства:
![]()
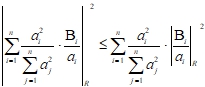 Отсюда следуют неравенства:
Отсюда следуют неравенства:
Литература
- Ф.Р.Гантмахер. «Теория матриц». часть I, II .Москва. “Наука”1988.
- Р.М.Мадрахимов, Ф.К.Атаев. «Коши-Буняковский тенгсизлигининг матрицавий аналоги» .Хоразм Маъмун академияси aхборотномаси.2008, № 3/4(8).9-11.
- Г.Г.Харди, Дж.Е.Литтльвуд и Г. Полиа. Неравенства. Москва Государственное издательство иностранной литературы. 1948 г.
- Bellman, A. Hoffman, A note on an inequality of Ostrowski and Taussky, Arkiv. Math., 5 (1954), 123-127.
- F.Beckenbach, An inequality for definite hermitian determinants, Bull. Am. Math. Soc., 35 (1929), 325-329/
- Hadamard, The psychology of invention in the mathematical field, Princeton, N.J., Princeton University Press, 1949.
- М. Рид, Б. Саймон. Функциональный анализ. 1-часть Издательство «Мир» Москва 1977.
