ESTIMATION AND CONTROL OF INTERFERING REFLECTIONS SPECTRUM PARAMETERS IN RADARS WITH QUASI-CONTINUOUS LIGHT EMISSION DURING ADAPTIVE ROBUST OBJECT OBSERVATION/TRACKING

Отмечаются устойчивые тенденции к расширению типажа, диапазонов высот, скоростей и маневренных возможностей воздушных объектов (ВО), являющихся в настоящий момент актуальными радиолокационными воздушными целями для авиационных бортовых РЛС. Постоянно усиливаются требования к РЛС по пропускной способности, дальности, точности, оперативности, помехоустойчивости при обнаружении, измерениях при «захвате» и сопровождении траектории ВО, причем эти требования необходимо выполнять в широком диапазоне возможных скоростей сближения/удаления ВО, включая нулевую и сверхзвуковые скорости, в условиях интенсивного маневра ВО, при малых отношениях сигнал/шум и мощных мешающих отражениях от земли (МОЗ)

На данный момент является актуальным и практически значимым решение проблемы обеспечения «всескоростного» обнаружения, высокоточного измерения траекторных параметров и устойчивого сопровождения маловысотных маневренных ВО в дальней и ближней зоне обзора РЛС при сложной сигнально-шумовой/помеховой обстановке. Известны адаптивно-робастные методы дальнего наблюдения (обнаружения/ «захвата» траектории) и сопровождения ВО на основе квазинепрерывного излучения (КНИ) с высокой или высокой средней частотой повторения импульсов (ЧПИ) и линейной частотной модуляцией несущего колебания в пачке импульсов (ЛЧМ)

При нахождении ВО в ближней зоне возникает необходимость более детального анализа и оценки параметров спектра МОЗ по БЛ, в т. ч. при движении и большой высоте РЛС, исследования возможностей рационального управления параметрами спектра МОЗ, использования «прозрачных» зон этого спектра в интересах решения задач РЛС в ближней зоне, учитывая что положение, границы и структура спектра МОЗ по БЛ и ГЛ в значительной степени:

• зависят от задаваемых параметров КНИ, вида и ориентации ДН, а также траекторных параметров РЛС;

• влияют на ограничения по минимальной дальности до малоскоростных/зависших ВО при применении типовых

Прагматической целью исследования является расширение функциональных возможностей РЛС в режиме КНИ с ЛЧМ при наблюдении/сопровождении ВО ближней зоне обзора в условиях мощных МОЗ – за счет устранения или существенного «смягчения» типичных ограничений по «слепым комбинациям» малых скоростей/дальностей ВЦ, зависящих от параметров спектра МОЗ.

Цель статьи – представить:

• нетрадиционную методику расчета параметров спектра МОЗ при КНИ с ЛЧМ, учитывающую эффекты нелинейной зависимости  ДДЧ от скорости/высоты РЛС, ширины и ориентации лучей ее ДН/дальностей до   «следов» БЛ и ГЛ  на поверхности, наличие экстремумов при отрицательных ЛЧМ, «расщепление» ДДЧ-спектра МОЗ и появление «прозрачных» (рабочих) зон ДДЧ;

• возможности рационального управления текущими параметрами спектра МОЗ с использованием предложенной методики путем адаптации КНИ (по ППИ и/или крутизне ЛЧМ), изменения траектории РЛС/ориентации ДН в процессе АР наблюдения/сопровождения ВО в ближней зоне.

В сеансе АР наблюдения

Диапазон «обслуживаемых» скоростей ВО при КНИ с ЛЧМ при S >0:

(1)

(2)

где 𝐹𝑟=(1/𝑇𝑟) - ЧПИ; 𝜆 - длина волны; 𝑅max – известная максимальная дальность обнаружения ВО, обеспечиваемая в РЛС. Учитывая возможное ускорение ВО aR ∈ [aR max (-); aR max (+)], где априорно aRmax(-)=-10g, aR max (+) = 10g, возможна и дополнительная неконтролируемая ЛЧМ эхосигнала ВЦ с крутизной вида

(3)

в диапазоне

(4)

Тогда, с учетом (3), (4) при предполагаемом факторе интенсивного маневра (ФИМ-факторе) ограничения

(5)

При S <0, напротив, более жесткие ограничения для отрицательных скоростей:

(6)

Присутствие ФИМ-фактора ведет к сокращению «наблюдаемого» диапазона скоростей ВО, однако в рассматриваемом диапазоне дальностей это сокращение, в совокупности, составляет не более десятка м/с и в диапазоне сверхзвуковых скоростей, обеспечиваемом при типовых параметрах КНИ с ЛЧМ можно считать несущественным.

Аналогично при маневрировании носителя РЛС появляется дополнительная ЛЧМ вида (3), обусловленная радиальными ускорениями по направлениям к «следам» БЛ, приводящая к дополнительным деформациям/смещениям в спектрах МОЗ по БЛ при КНИ с заданной ЛЧМ. Эти ускорения определяются по данным микронавигационной системы РЛС

Рассматриваемая ориентация ДН предполагает, что присутствуют МОЗ по БЛ, формируемые сигналами от «наступающих» (или неподвижных при зависшей РЛС) фрагментов земной поверхности. В общем случае, при большом азимутальном отклонении ГЛ от вектора путевой скорости РЛС (при переднебоковом/боковом обзоре) возможны и «отступающие» следы ряда БЛ. Эти ситуации в работе не рассматриваются.  Для каждого k-го БЛ направление горизонтальной проекции его оси характеризуется азимутальным углом α(k) относительно вектора скорости РЛС W и проекция скорости на это азимутальное направление V(k)= W cos α(k).  Доплеровская частота (ДЧ) FDSL(k) по оси БЛ с углом наклона βSL(k) и диапазон ДЧ по ширине БЛ 2ΔβSL(k):

(7)

(8)

где βSL(k)+ΔβSL(k)=βSLmax(k) и βSL(k)-ΔβSL(k)=βSLmin(k) – соответственно максимальный и минимальный углы наклона по направлению ближней и дальней границам «следа» k-го БЛ в пределах его угловой ширины в вертикальной плоскости.

Для КНИ с крутизной ЛЧМ Sдальностно-доплеровская частота (ДДЧ)FRD0 SL(k) по оси БЛ, а также ДДЧ FRD1 SL(k) и FRD2 SL(k) по направлениям к ближней и дальней границе «следа» БЛ, соответственно:

(9)

(10)

(11)

В работах

В сравнении со спектром доплеровских частот МОЗ по БЛ при типовом КНИ (S=0), при КНИ с ЛЧМ спектр ДДЧ этих МОЗ смещается и расширяется, причем при S <0 спектр уже, чем при S>0.

Отметим, что «мощные» МОЗ, как правило, формируется только направлениям «первых» и «вторых» БЛ в ДН и, соответственно, спектр ДДЧ при окологоризонтной ориентации ГЛ локализуется в границах, определяемых при малых (не более 10о…15о) углах наклона БЛ и небольших азимутальных отклонениях от оси ГЛ для этих БЛ, т. е. при циклическом выполнении процедур вида (9)-(13) для двух «первых» и двух «вторых» при известной ориентации оси ГЛ, скорости, высоте РЛС и ширине лепестков в ДН РЛС. В ряде типовых ДН все направленные вниз БЛ совпадают по азимуту с направлением оси ГЛ (см. рис. 1). В таком случае для МОЗ по БЛ расчет (12) - (14) выполняется по двум БЛ при одном азимуте и также при малых углах их наклона, когда влияние ЛЧМ на деформацию спектра наиболее интенсивно. 

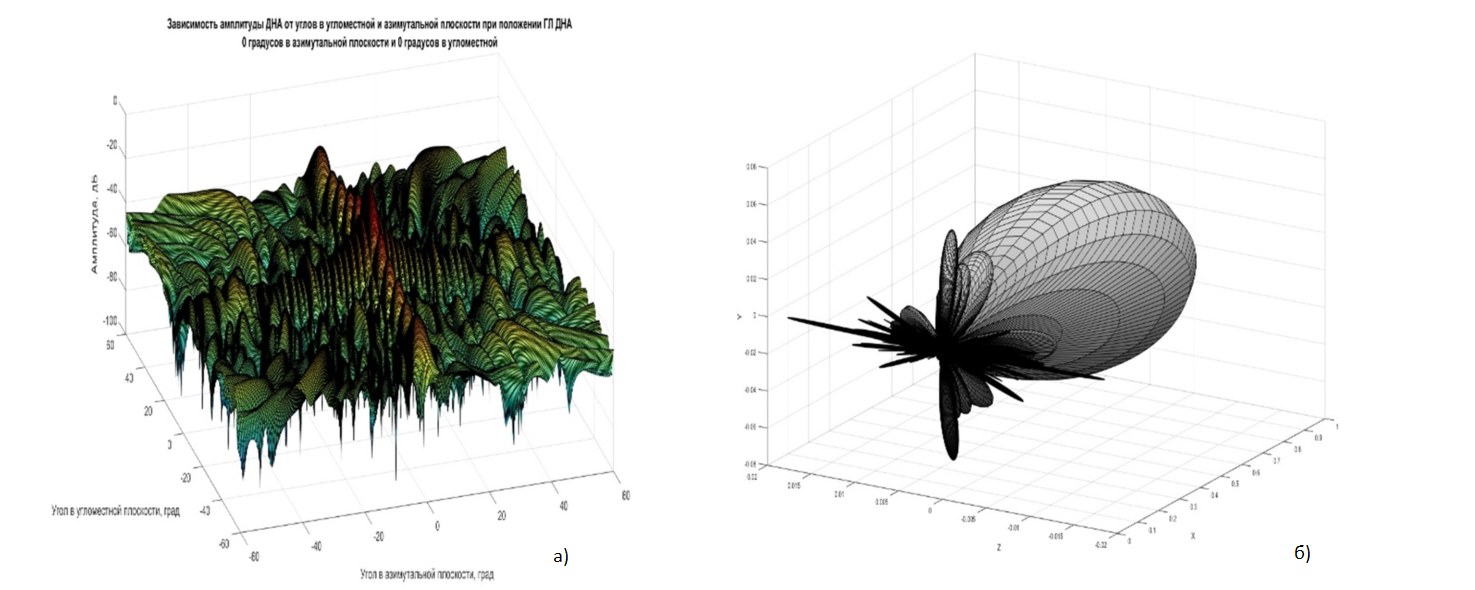
Рисунок 1 - Распределение амплитуд в зависимости от азимута/угла места и  вид пространственной ДН

Примечание: а – в зависимости от азимута/угла места; б – вид пространственной ДН

DOI:10.60797/IRJ.2024.145.45.1

При S <0 есть экстремум ДДЧ при угле наклона β*SL(k) при условии:  из которого следует

или 

(12)

При подстановке  это выражение имеет вид  который преобразуется в двучленное кубическое уравнение X3+pX+q=0, где p=(B/A), q=(-B/A), решение которого находится по формуле Кардано

Искомый угол β*SL(k) и соответствующая ему дальность R*SL(k) в данном БЛ:

(13)

Из соотношений вида (9)-(11) с учетом (7), (8) также следует, что при известных значениях высоты РЛС, угла наклона БЛ и крутизны S <0 граница  скоростной проекции V*(k), ниже которой ДДЧ FRD0 SL(k) <0:

(14)

Например, при S= -20 кГц/мс, βSL(k) =2о, Н=1000 м    значение V*(k) ≈57,3 м/с, ниже которой ДДЧ уже отрицательная и «видимая» ДДЧ будет проявляться уже вблизи значения ЧПИ.

При малом угле наклона/протяженном следе БЛ в каждом дискрете неоднозначной задержки сигнала (НЗС) в рабочей зоне ППИ с шириной dτ = τpulse /kскс, в общем случае, присутствуют сигналы от нескольких дистанцированных полос поверхности в границах следа. Расстояния до этих полос соответствуют разным индексам ППИ r. Как следствие, при суперпозиции сигналов в дискрете НЗС при КНИ с ЛЧМ будут наблюдаться относительно узкие и разнесенные спектры для ДДЧ по сигналам от разных полос, причем интервал ΔFRD(r/r-1) между ближними максимумами амплитуды сигнала на ДДЧ FRD(r) и FRD(r-1):

(15)

где ΔFD(r/r-1) = FRD(r) - FRD(r-1) –  приращение ДЧ, обусловленных радиальными скоростями по направлениям к центрам полос поверхности на дальностях, соответствующих индексам ППИ r и r-1. Заметим, что ширина интервала (15) может составлять сотни Гц. Например, только компонента S Tr при типовых параметрах КНИ

Таким образом, основные результаты заключаются в том, что:

• предложена оригинальная процедура аналитического оценивания границ спектра МОЗ при КНИ с отрицательной ЛЧМ – на основе решения кубического уравнения относительно углов наклона лучей/дальностей до земли, определяющих экстремальную ДДЧ в спектре МОЗ;

• показаны: наличие «прозрачных» зон ДДЧ в границах спектра МОЗ; расчет их положения, ширины и   возможность их использования для наблюдения/сопровождении ВО в ближней зоне на фоне МОЗ.

Новизна полученных результатов заключается в учете эффектов «нелинейности» и «расщепления» ДДЧ-спектров МОЗ при оценке его параметров и обосновании возможности адаптивного управления параметрами спектра МОЗ для расширения функциональных возможностей РЛС в ближней зоне обзора на фоне МОЗ.         

Приведенные в литературе типовые процедуры определения границ спектра и режекции МОЗ по БЛ ориентированы на решение задач наблюдения/сопровождения ВЦ в дальней зоне, полностью исключают из обработки все ДДЧ от нуля до границы спектра при максимальной дальности до земли в «следах» БЛ. При этом режекция осуществляется с «запасом», без учета экстремума при формировании спектра МОЗ при отрицательной крутизне ЛЧМ, «прозрачных» зон ДДЧ в рамках спектра каждого БЛ и между БЛ. Для дальнего наблюдения ВЦ, при малой высоте и скорости РЛС такая упрощенная режекция МОЗ не является критичной, но в других ситуациях (в ближней зоне, большей высоте/скорости РЛС) может существенно ограничивать возможности наблюдения ВЦ. Представленные в работе результаты анализа и методика определения параметров спектра МОЗ по БЛ позволяют учесть указанные факторы, осуществить уточненную и избирательную режекцию МОЗ, расширить возможности наблюдения малоскоростных/зависших ВЦ в ближней зоне, в т.ч. и при целенаправленном управлении параметрами КНИ, влияющими на структуру, положение и границы спектра МОЗ по БЛ.