LAYER HEAT-AND-MASS TRANSFER IN LOCALLY NONEQUILIBRIUM RELAXATION MICROSTRUCTURE ENVIRONMENT

ПОГРАНСЛОЙНЫЙ ТЕПЛОМАССОПЕРЕНОС В СРЕДАХ ЛОКАЛЬНО-НЕРАВНОВЕСНОЙ РЕЛАКСАЦИОННОЙ МИКРОСТРУКТУРЫ

Научная статья

Попов В.И.^*

Институт теплофизики им. С.С. Кутателадзе СО РАН, Новосибирск, Россия

^* Корреспондирующий автор (vi1popov[at]mail.ru )

Аннотация

Методом интегральных соотношений рассмотрено влияние локальной неравновесности среды с релаксационной микроструктурой на погранслойное движение и тепломассоперенос. Классическое исследование задачи расширено на реологический класс полимерных сред и их систем с неравновесной релаксационной микроструктурой в поле сдвиговых, энтропийных и диффузионных сил. Термодинамические потоки в этом случае уже не определяются только градиентом соответствующего потенциала переноса, как для бесструктурных сред, а являются решениями эволюционного уравнения для внутреннего релаксационного параметра среды. Выделены определяющие процесс режимы, проанализированы и получены закономерности влияния локально – неравновесного, (запаздывающего), релаксационного процесса переноса на характеристики безградиентного погранслойного движения и тепломассопереноса.

Ключевые слова: полимерные среды, микроструктура, локальная – неравновесность, релаксация напряжений, погранслойный тепломассоперенос.

LAYER HEAT-AND-MASS TRANSFER IN LOCALLY NONEQUILIBRIUM RELAXATION MICROSTRUCTURE ENVIRONMENT

Research article

Popov V.I.^*

Kutateladze Institute of Thermophysics of the Siberian Branch of Russian Academy of Sciences, Novosibirsk, Russia

^* Corresponding author (vi1popov[at]mail.ru)

Abstract

By the method of integral relations, the influence of the local nonequilibrium state and relaxation microstructure on the border-layer movement and heat and mass transfer is considered. The classical study of the problem is extended to the rheological class of polymer environments and their systems with non-equilibrium relaxation microstructure in the field of shift, entropy and diffusion forces. Thermodynamic flows in this case are no longer determined by the gradient of the corresponding transfer potential alone, as in structureless environments, but are themselves solutions of the evolutionary equation for the internal relaxation parameter of the environment. The modes determining the process have been listed, the regularities of influence of local nonequilibrium, (delayed), as well as relaxation process of transfer on the characteristics of the boundless border movement and heat and mass transfer have been analyzed and obtained.

Keywords: polymer environment, microstructure, local–nonequilibrium, stress relaxation, border-layer heat-and-mass transfer.

Введение

Широкий класс сред с неравновесной микроструктурой расплавы и растворы полимеров, сополимеры, вязкоупругие нефти, коллойдные системы, эмульсии, латексы, краски, полимеризованные смесевые топлива, и различные модификации таких сред наделены сложной внутренней микроструктурой и вследствие этого имеют особые физико – химические свойства. В зависимости от условий деформирования, даже вблизи равновесия, они способны проявлять нелинейно – вязкие свойства, запасать подводимую из вне механическую энергию в виде разностей нормальных компонентов девиатора тензора напряжений и релаксировать напряженное состояние [1],[2]. Следствием этих свойств являются немгновенные и нелокальные (запаздывающие) отклики среды на внешние возмущения, определяющие процессы переноса потока импульса, тепла и массы к состоянию равновесия. Учет и оценка запаздывающих явлений переноса в технологиях получения и переработки рассматриваемых систем позволит ими управлять, оптимизировать и интенсифицировать.

Несмотря на большое разнообразие таких сред, и геометрий течений, для них характерно общее фундаментальное свойство: все процессы переноса необратимо по релаксационному механизму направлены на нейтрализацию внешних возмущений, отклоняющих структурную систему от состояния термодинамического равновесия.

 В отличие от бесструктурных сред, рассматриваемая проблема осложнена тем, что структурные системы, из-за релаксационных явлений, откликаются на внешние возмущения немгновенно во времени и нелокально в пространстве, неравновесно даже в малом дифференциальном объеме среды, деформационное состояние которой зависит от состояния ближайшего окружения. Проблема немгновенности и дальнодействия возникает уже на уровне реологического замыкания динамического уравнения сохранения импульса (количества движения), тепла и массы элементарного объема таких сред, в том числе с учетом их микроструктурных состояний [3],[4],[5].

 Прикладные задачи о влиянии локально – неравновесных процессов переноса на погранслойное движение и тепломассоперенос возникают в технологических процессах полимерных покрытий изделий от коррозии методом погружения, улучшения триботехнических свойств материалов, для качественного поверхностного слоя покрытий на подложке, включая многослойные покрытия, с целью повышения прочности модифицированных поверхностных слоев с релаксацией напряжений.

Важность задачи дополняется тем, что при получении качественного адгезионного покрытия и однородного распределения модифицирующих микро и нанодобавок, и прогнозируемой микроструктуры, необходимо иметь параметры согласования времени технологического процесса и времени релаксации полимерных систем к новому равновесному состоянию. Неучет запаздывающих релаксационных явлений на процессы тепломассопереноса может привести к потере качества поверхностной адгезии, а также к термической деструкции в полимерных средах и их системах из-за тонко сбалансированных сдвиговых, энтропийных и диффузионных сил.

Метод интегральных соотношений часто используется при анализе характеристик погранслойного движения, сопротивления, тепло и массопереноса для обычных бесструктурных сред [6], [7]. Это связано с математическими трудностями, которые возникают уже при совместном интегрировании нелинейных дифференциальных уравнений погранслойного движения и тепломассопереноса, несмотря на простейшее (мгновенное и локально – равновесное) реологическое уравнение состояния Ньютона, относительно потока с сопряженными с ними силами.

 Закономерности движения и тепломассопереноса при внешнем обтекании тел потоком сред с неравновесной внутренней микроструктурой практически не изучены. Реодинамическая проблема, как уже отмечено, состоит в замыкании динамического закона сохранения импульсов реологическим уравнением состояния, в разработке инженерных методов расчета процессов переноса.

Основная цель работы состоит в расширении известных интегральных методов переноса импульса и энергии применительно к исследованию квазистационарных погранслойных процессов переноса для широкого класса полимерных сред и их систем с релаксационной микроструктурой в поле сдвиговых, энтропийных и диффузионных сил. В установлении режимов и закономерностей, позволяющих учитывать влияние локально-неравновесных (запаздывающих) релаксационных процессов переноса импульса на примере характеристик плоского безградиентного погранслойного движения и тепломассопереноса.

Интегральные соотношения импульсов и теплового потока для пограничного слоя

Интегральное соотношение импульсов плоского квазистационарного погранслойного движения рассматриваемых сред и их систем, когда инерционные силы доминируют над внутренними напряжениями, представлено в работе [8] в виде:

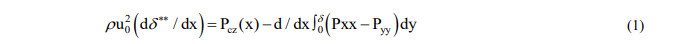
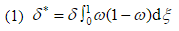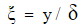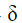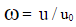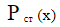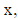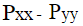В уравнении  – толщина потери импульса, где   – координата, отнесенная к толщине пограничного слоя – . Величина  – отношение продольной скорости к скорости невозмущенного стенкой потока; ρ – плотность среды;  – касательное напряжение сдвига на стенке (у = 0) , переменное по продольной координате  а  первая разность нормальных компонент девиатора тензора напряжений.

Естественное введение в теорию второго члена правой части уравнения (1) – первой разности нормальных компонент тензора напряжений, которая обычно проявляется в опытах, включая простые реометрические исследования, устраняет неопределенность неизвестного изотропного гидростатического давления (P₀ ) и расширяет возможность его использования для исследования полимерных сред со сложной внутренней микроструктурой [2].

Поле течения во внешней области обтекаемого тела со скоростью u₀ , как это обычно предполагается в теории погранслойного движения (1/ Re<<1), описывается решением уравнения Эйлера.

Величина 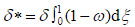  – толщина вытеснения. Она характеризует смещение линий тока от поверхности обтекаемого контура, вызванное наличием пограничного слоя и позволяет дать практическую оценку характерной толщины пограничного слоя, полагая, как обычно, что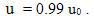 

Влияние локально – неравновесного процесса переноса импульса на тепловые характеристики пограничного слоя определяется из интегрального соотношения для теплопереноса с постоянными теплофизическими свойствами [9]:

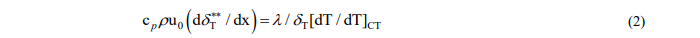
В уравнении 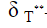– толщина потери теплосодержания; 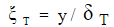координата, отнесенная к толщине теплового пограничного слоя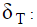

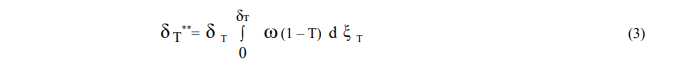
Уравнение (1) не замкнуто относительно реологического уравнения состояния, характеризующее связь между потоком импульса и сопряженными с ними силами. Кроме того уравнения (1), (2), (3) неопределенны относительно распределения по сечению погранслоя профиля скоростей и температур.

Реологическое уравнение состояния и режимы погранслойного движения

Реодинамика определяет процессы движения и тепломассопереноса. Подходы и методы описания кинематики деформирования рассматриваемых сред и процессов переноса в них зависят от вида реакции среды на внешнее возмущение. В настоящее время развиваются феноменологические и структурно – статистические подходы и методы для реологического замыкания фундаментальных динамических законов сохранения.

В работе [3] в рамках расширенной неравновесной статистической термодинамики для класса полимерных сред и их систем смоделирован немгновенный и нелокальный процесс переноса потока импульса сред с релаксационной микроструктурой в поле сдвиговых, энтропийных и диффузионных сил. Получены соотношения для компонентов тензорного макропараметра, характеризующие изменение структуры деформируемой среды из-за релаксационных явлений. При этом согласующиеся с квазистационарным опытом [10] соответствующие компоненты тензора напряжений потока импульса с сопряженными с ними силами, имеют вид:

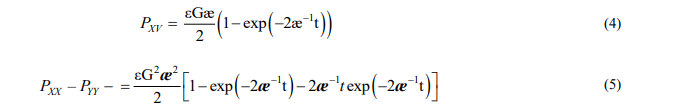
Анализ соотношений (4) и (5) выявил зависимость сдвиговых и первой разности нормальных компонент тензора напряжений от релаксационных свойств и режимов деформирования среды. Очевидно (рис.1), что при чисах 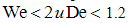к расчету процессов переноса можно применять методы классической неравновесной термодинамики. В нестационарных потоках в области чисел  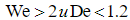диссипативные реологические потоки не определяются градиентами соответствующего потенциала переноса, а уже являются решениями эволюционного уравнения, описывающего процесс релаксации напряженного состояния неравновесной полимерной системы к своим равновесным значениям.

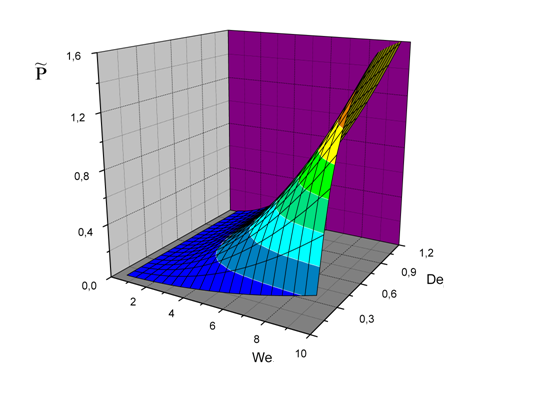
Рис. 1 – Влияние Dе и Wе на величину и характер изменения первой разности
нормальных компонент тензора напряжения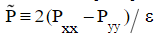 

 Немгновенное влияния на процесс переноса импульса характеризует критерий Деборы (отношение времени релаксации 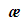 к характерному времени процесса  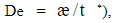а локально – неравновесное влияния в квазистационарном процессе характеризует критерий Вейссенберга  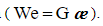Величины 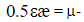динамическая вязкость; – модуль эластичности; градиент скорости сдвига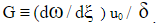 

Из соотношений (4) и (5) следует, что в условиях квазистационарного сдвига, характерного для интегрального погранслойного класса задач [6], [7], напряженное состояние среды, обусловленное локально-неравновесной микроструктурой, имеет вид:

Таким образом, критерий We является мерой относительного влияния первой разности нормальных и касательных напряжений, развивающихся в потоке в балансе с инерционными силами. Диссипация механической энергии – величина 

В работе [10], на основе обработки экспериментальных данных различных авторов в рамках соотношения (6) представлен широкий набор полимерных сред и их систем, (рис. 2), для которых это отношение является постоянной
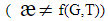величиной.

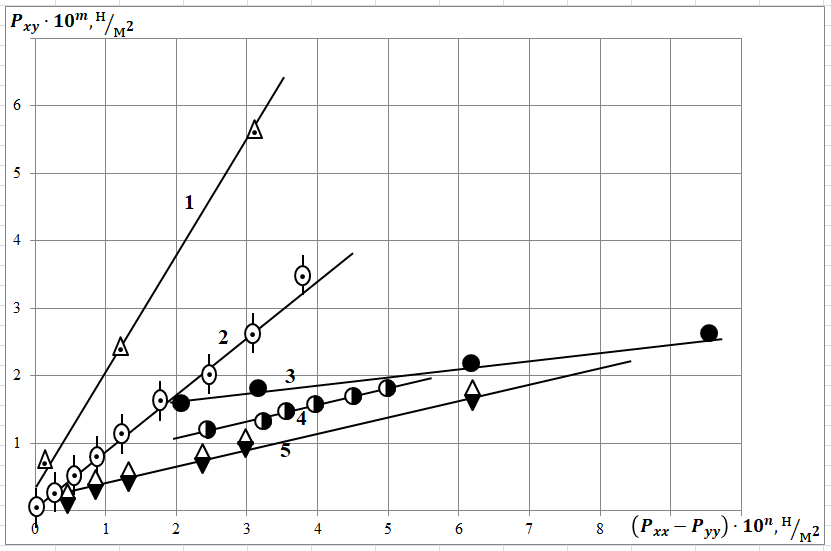
Рис. 2 – Зависимость между касательными и первой разностью нормальных напряжений:
1 – 0.5 % – полиизобутилметакрилат в дибутилфталате, m = – 3, n= – 4; 2 – 11% раствор этилцеллюлозы в циклогексане, m = – 2, n= – 2; 3 – 0.7% раствор Na-КМЦ в воде, m = 1, n=0; 4 – 5% раствор полиизобутилена в декалине, m = 0, n = – 1; 5 – жидкость Ankle- Joint, m = – 1, n= – 3

Результаты исследования влияния локально – неравновесного процесса переноса импульса на интегральные характеристики погранслойного движения и тепломассопереноса

Выше отмечено, что уравнения (1), (2), (3) неопределенны относительно распределения по сечению погранслоя профиля скоростей и температур. В методе интегральных соотношений обычно предполагается аппроксимация поля скоростей и температур (концентрационных масс) поперек пограничного слоя с последующим нахождением их толщин и интегральных характеристик потока по длине их развития [6], [7], [9]. Вследствие аналогичности граничных условий делается предположение о подобном характере распределения профилей скоростей и температур. Коэффициенты аппроксимации определяются из граничных условий задачи.

Распределение скоростей для рассматриваемой задачи удобно выбрать в виде ряда кубической параболы [6] для граничных условий: 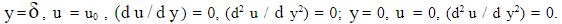Полагаем, что в непосредственной близости от стенки касательные напряжения постоянны. В соответствии с (4) должны быть постоянны градиенты скорости, что соответствует последнему граничному условию непрерывности изменении кривизны профиля скоростей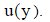

Перечисленным требованиям будет удовлетворять безразмерное распределение продольной составляющей вектора скорости в виде [6]:

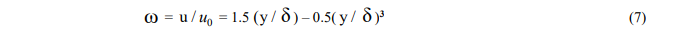
Развитие слоя с передней кромки ( х=0 ) торможения потока может происходить лишь после диссипативного 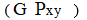[8]  релаксационного завершения процесса от квазитвердого (эластичного) до некоторого жидкотекучего состояния напряжений в потоке  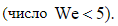В этом случае последний член в уравнении (1) уже не является доминирующим, а силы инерции уравновешиваются напряжениями сдвига и частично первой разностью нормальных напряжений (6) [2], [11].

Подставляя соответствующие значения величин (4), (5), (7) в соотношение (1), в котором уже 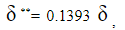 приходим к замкнутому уравнению импульсов для определения развития толщины погранслоя вдоль продольной координаты х.

Из интегрального соотношения импульсов (1), а также из условия постоянства величины We [ 10 ] для локально – неравновесного потока, когда последний член в уравнении (1) не является доминирующим ( область 2 < We < 5, рис. 1) имеем:

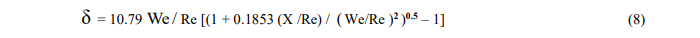
Уравнение (8) определяет развитие толщины погранслоя вдоль пластины (Х= Х / L), в зависимости от чисел 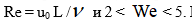Величина 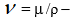– кинематическая вязкость среды. В уравнении (8) толщина пограничного слоя отнесена к характерному геометрическому размеру L . Локально – равновесный поток имеет место при We < 2 . В этом случае влияние первой разности нормальных напряжений незначительно (рис.1).

Критерий 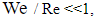 на основе лишь анализа размерностей погранслойного движения уже предлагался в работе [2] к систематическому использованию. В данной работе методом интегральных соотношений установлено на основе этого критерия запаздывающее влияние по релаксационному механизму внешнего возмущения на процессы погранслойного тепломассопереноса. Отношение  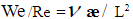не зависит от Х и скорости потока. Его можно интерпретировать, как свойство среды терять сдвиговый вязкий импульс в результате релаксационных явлений на масштабе L².

Для локально – равновесного потока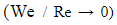 из (8) имеем уже известные соотношения развития ( без релаксационного запаздывания ) толщины погранслоя по длине пластины 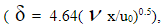сопротивления ньютоновских жидкостей [6], [7].

Из соотношения (8) также следует, что с увеличением толщина динамического погранслоя уменьшается, с ростом частоты релаксации – возрастает. Это может быть средством управления его толщиной и соответственно сопротивлением потока.

В связи с тем, что граничные условия профиля температур в уравнениях (2) и (3) аналогичны граничным условиям для профиля скоростей (7), полагаем [12]:

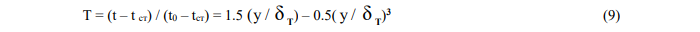
В уравнении (9) t _ст и t₀ соответственно постоянные температуры на стенке и вне теплового пограничного слоя. Температура среды отсчитывается от температуры стенки.

Для полимерных сред и их систем толщина теплового пограничного слоя меньше динамического, то есть 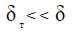В силу тождественности начальных 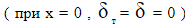и граничных  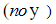условий их определения, можно полагать, что толщины теплового и динамического слоев в изотермическом приближении зависят от х одинаково, а отношение  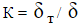имеет постоянную величину [5], [12].

Определяя величины в пределах теплового пограничного слоя, и подставляя их в уравнение теплового баланса (2), приходим для области значений We  / Re <<1 и 2 < We < 5 к уравнению для нахождения К и уравнению для развития толщины теплового погранслоя:

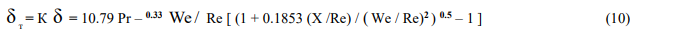
Для локально-равновесного потока из (10) имеем [12]: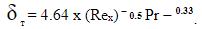 

Коэффициент теплоотдачи, по общепринятому опытному определению [9], [12], имеет вид:

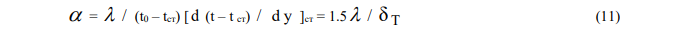
Следовательно, с учетом (10) соотношение для критерия Нуссельта 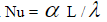 имеет вид:

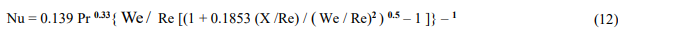
Без релаксационного запаздывания (локально – равновесный поток, We / Re → 0) из (12) имеем соотношения [6], [12] для ньютоновских сред:

Из уравнения (10) и (11) следует, что с ростом времени релаксации среды толщина теплового погранслоя уменьшается, коэффициент теплоотдачи возрастает. С ростом частоты релаксации соответственно увеличивается. Тепломассоперенос (12) при этом может соответственно увеличивается или уменьшаться.

Выводы

Интегральные методы переноса потока импульса и энергии расширены применительно к исследованию квазистационарных погранслойных характеристик переноса в средах локально – неравновесной релаксационной микроструктуры. Получены аналитические закономерности для учета запаздывающего влияния неравновесности на основные характеристики погранслойного движения и тепломассопереноса. Выявлены режимы и критерии подобия 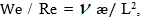позволяющие оценить и учесть влияние запаздывающих релаксационных процессов переноса импульса на характеристики безградиентного погранслойного движения и тепломассопереноса. Установлено, что величина We является мерой относительного влияния первой разности нормальных и касательных напряжений, развивающихся в потоке в балансе с инерционными силами. Величину  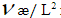можно интерпретировать, как свойство среды терять сдвиговый вязкий импульс на пространственном масштабе L² в результате релаксационного явления переноса, обусловленного диссипацией механической энергии потока. Учет влияния времени или частоты релаксации устанавливает возможность управления толщиной теплового пограничного слоя и соответственно тепломассопереносом при внешнем обтекании поверхности средой локально – неравновесной релаксационной микроструктуры.

 

Конфликт интересов  Не указан.

Conflict of Interest  None declared.