ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВ НА НЕПОЛНЫХ И НЕЛИКВИДНЫХ РЫНКАХ
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВ НА НЕПОЛНЫХ И НЕЛИКВИДНЫХ РЫНКАХ
Научная статья
Ефремов В.А.
Ассистент кафедры автоматизированных систем управления, Томский государственный университет систем управления и радиоэлектроники
Аннотация
Проведен анализ проблем адаптивного ценообразования опционов на российском финансовом рынке. Предложен адаптивный алгоритм оценки справедливой стоимости опционов на неполных и неликвидных рынках.
Ключевые слова: деривативы, ценообразование опционов, структурированные финансовые продукты.
Keywords: derivatives, options valuation, structured products.
Финансовый рынок является полным, если на нем обращается достаточное количество разнообразных финансовых инструментов, необходимое для формирования безрискового портфеля в любых условиях. В таком случае для любого финансового продукта можно подобрать хеджирующий портфель так, что инвестиции перестанут зависеть от риска [1].
Российский финансовый рынок является неполным, так как не отвечает критериям полноты. Этот факт приводит к риск-нейтральному подходу ценообразования деривативов, лежащих в основе структурированных продуктов.
В настоящее время нет ни одной математической модели, которая может применяться для описания всех логарифмических доходностей базовых активов. Динамика цен любого актива отличается от других своими особенностями, которые необходимо учитывать при ее моделировании.
Оценка структурированных продуктов предполагает, что лежащие в их основе производные финансовые инструменты могут содержать абсолютно разные базовые активы. Таким образом, возникает задача адаптивного ценообразования деривативов, которая поможет оценивать структурированные продукты вне зависимости от базового актива. В настоящее время оценка справедливой стоимости деривативов так же не учитывает особенности динамики цен их базовых активов – она использует нормальный закон распределения во всех случаях.
Неполные рынки характеризуются скачками различной величины и, как правило, динамика цен их активов не может быть описана нормальным законом распределения. Данный факт обуславливает применение модели логарифмических доходностей базовых активов [2] при адаптивном ценообразовании деривативов.
Система поддержки принятия решений инвестора при выборе структурированных финансовых продуктов [3], оценивает только те структурированные продукты, которые включают в себя портфель опционов на базовые активы, представленные на российском рынке.
Справедливая оценка опциона на неполных рынках основывается на выборе модели логарифмических доходностей его актива и подборе ее параметров. Калибровка выбранной модели может основываться на одном из двух подходов:
− калибровка модели таким образом, чтобы полученные цены опционов были как можно ближе к их рыночным ценам;
− калибровка модели к эмпирическим данным логарифмических доходностей базового актива.
Российский рынок опционов нельзя назвать ликвидным, так как его объемы сделок пока еще низки, по сравнению с рынком фьючерсов, индексов или акций [1]. Данный факт обуславливает применение второго подхода к калибровке модели логарифмических доходностей базовых активов [2].
Адаптивный алгоритм справедливой оценки опциона на неполных и неликвидных рынках (рис. 1) состоит из следующих шагов.
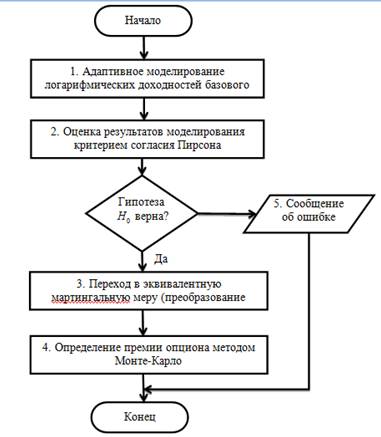
Рис. 1 Адаптивный алгоритм оценки справедливой стоимости опционов на неполных и неликвидных рынках
1. Адаптивное моделирование логарифмических доходностей базового актива, лежащего в основе опциона. На данной стадии используется модель [2].
2. На следующем этапе происходит проверка гипотезы H0 о том, что эмпирические данные согласованны с моделью, полученной на первом шаге.
2.1 Если гипотеза H0 верна, то переходим к шагу 3.
2.2 Если гипотеза H0 ложна, то справедливое ценообразование опциона с использованием такой модели не возможно, и происходит вывод сообщения об ошибке.
3. На данном шаге происходит переход в эквивалентную мартингальную меру Q, с помощью преобразования Эсшера [4]. Триплет Леви преобразовывается путем численного решения уравнения (1) относительно единственной переменной h методом Брента и подстановки h* значения в (2) и (3).
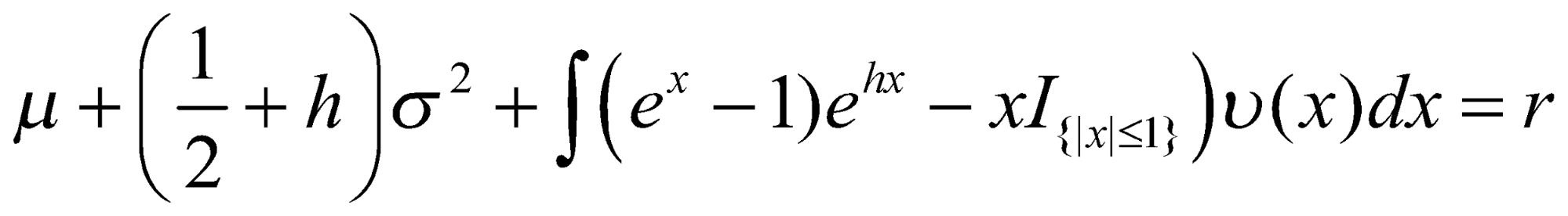 (1)
(1)
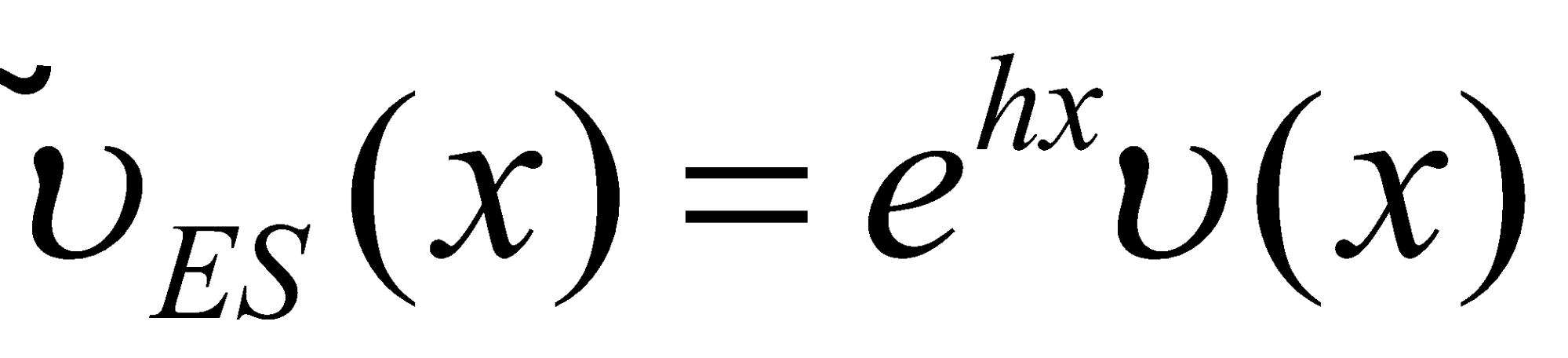 (2)
(2)
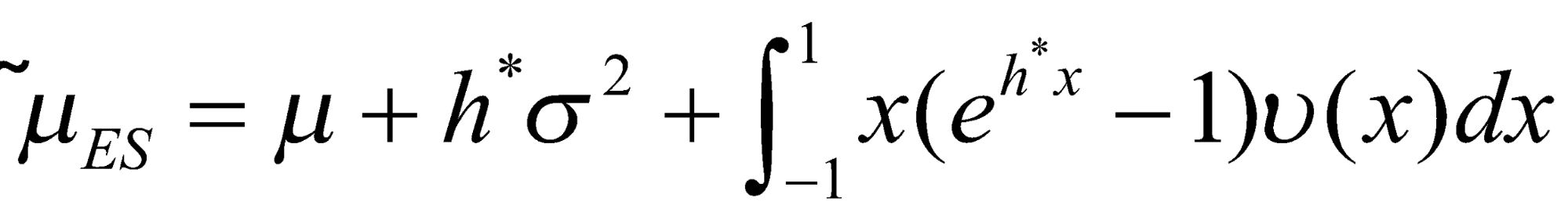 (3)
(3)
где r – безрисковая процентная ставка и h – корень уравнения (1). Подставлять в (2) и (3) можно любой из найденных корней уравнения (1), так как множеству решений соответствует множество эквивалентных мартингальная мер на неполных рынках.
4. Завершающем этапом является определение премии опциона методом Монте-Карло. Этот метод заключается в генерации большого числа возможных значений цены базового актива на момент экспирации опционного контракта и вычислении среднего значения его доходов дисконтированного по безрисковой процентной ставке .
Выводы
Разнообразие производных финансовых продуктов и базовых активов затрудняет справедливую оценку их стоимости. Это обусловлено тем, что каждый базовый актив имеет отличительные особенности в своей ценовой динамике.
Ценообразование структурированных продуктов предполагает оценку всех его деривативов, которая сводиться к выбору стохастической модели логарифмических доходностей базовых активов и ее калибровке. Такой процесс является трудоемким и требует участия финансовых инженеров.
Представленный адаптивный алгоритм справедливой оценки опционов, позволяет системе поддержки принятия решений инвестора при управлении капиталом с использованием структурированных финансовых продуктов [3] в автоматическом режиме учитывать особенности динамики цен базовых активов при их моделировании.
Список литературы / References
- Морозова М. М. Моделирование и анализ эффективности ценообразования опционов на российском рынке: дисс. канд. экон. наук / Институт экономики и организации промышленного производства Сибирского отделения Российской академии наук. – Новосибирск, 2010. – 203 с.
- Ефремов В.А. Моделирование финансовых временных рядов на основе процессов Леви для определения премий опционных контрактов // Международный научно-исследовательский журнал. – Екатеринбург. – 2012. – № 4. – С. 7-11.
- Ефремов В.А., Система поддержки принятия решения инвестора при выборе структурированных финансовых продуктов контрактов // Международный научно-исследовательский журнал. – Екатеринбург. – 2012. – №5. – C. 138-140.
- Miyahara Y. Martingale measures for the geometric Levy process models. – Nagoya City University, 2005. – 14 p
