Predictive study of cobalt precipitation yield, impurities, and magnesia consumption by mathematical modeling during primary decobaltation for an oxide ore
Predictive study of cobalt precipitation yield, impurities, and magnesia consumption by mathematical modeling during primary decobaltation for an oxide ore
Abstract
This article presents the results of a predictive study on the precipitation performance of cobalt, impurities, and magnesium consumption during primary decobalting for a case of a copper-cobalt ore from Tenke Fungurume Mining. To achieve this, we conducted a black box modeling following a centered composite plan (response surface design), which requires 5 levels for each factor (-α, -1, 0, +1 + α). To evaluate the quadratic effects, we opted for the criterion of uniform precision α equals 1.68. In real variables, these values correspond to (6.8; 7.1; 7.55; 8; 8.3) for pH; (31.6; 35; 40; 45; 48.4) °C for temperature, and (11.6; 13; 15; 17; 18.4)% for the solid percentage of magnesium. Mathematical modeling using experimental data led us to develop a total of 7 mathematical models, of which 2 models accurately represent the process (Mn precipitation yield and magnesia consumption). The graphical tool showed us that when considering the linear effects of factors, we observe that the precipitation yield of aluminum, magnesium, and iron is more influenced by temperature; the precipitation yield of copper is more influenced by the solid percentage of magnesia; the precipitation yield of manganese is more influenced by pH; the precipitation yield of cobalt is significantly more influenced by pH and solid percentage; regarding magnesia consumption, we found that extreme values (1.68) of factors are the basis for high magnesia consumption.
1. Introduction
The term "cobalt" originates from the German folklore Kobold, referring to malevolent subterranean spirits. This nomenclature arose because ancient metallurgists, unfamiliar with cobalt's properties, encountered adverse health effects during its extraction
. Cobalt is a silver-gray transition metal characterized by several notable properties, including ferromagnetism, high hardness and wear resistance when alloyed, low thermal and electrical conductivity, high melting point, multiple oxidation states, and the ability to produce vivid blue pigments when combined with silica .Cobalt plays a critical role in modern technology, primarily serving as a key component in rechargeable battery cathodes and superalloys for jet engine turbines. Global cobalt consumption reached approximately 75,000 metric tons in 2011
. While historically utilized for coloring ceramics, glass, and textiles, cobalt now has extensive applications across environmental, industrial, high-tech, medical, and strategic sectors . The recovery of cobalt from ores involves various metallurgical processes, with hydrometallurgical methods being predominant . These processes typically employ precipitation to eliminate impurities before isolating cobalt hydroxide .Precipitation is a chemical separation technique wherein dissolved metal cations react with specific anions upon the addition of a precipitating agent, forming an insoluble solid (precipitate) . This method facilitates the recovery of metals such as cobalt, copper, and zinc. Common precipitating agents include calcium hydroxide (Ca (OH)₂), magnesium hydroxide (Mg(OH)₂), sodium hydroxide (NaOH), and ammonium hydroxide (NH₄OH) . The general reaction for metal hydroxide precipitation is as follows:
In this study, magnesium hydroxide was selected as the precipitating agent.
Coprecipitation is defined as the concurrent removal of an ion alongside another with which it does not inherently form a precipitate
. This phenomenon can occur through multiple mechanisms, including the incorporation of an ion as an impurity within the crystalline lattice of another compound, the adsorption of an ion onto the surface of another crystalline phase, or simultaneous precipitation at an equivalent pH , . Consequently, the separation of cobalt represents a critical stage in the metallurgical processing of cupro-cobalt ores, as it facilitates the isolation of cobalt from other metal impurities in solution via precipitation using an appropriate precipitating agent , , .To optimize this process, a modeling approach will be employed to evaluate key parameters. As demonstrated by Yahiaoui and Idri
, a composite experimental design a class of response surface methodology (RSM) can be utilized to fit second-order models effectively . Composite designs, which belong to a broader category of experimental frameworks , serve several essential functions: identifying significant factors, generating high-precision predictions, detecting model lack-of-fit with high sensitivity, locating optimal response conditions or regions, and enabling a sequential experimental workflow , .In the Democratic Republic of the Congo (DRC), particularly within the Haut Katanga province, cobalt production undergoes a multi-stage refining process aimed at enhancing the quality of the final product, cobalt hydroxide
, , .This process involves systematic removal of impurities prior to the final recovery stage , . Nevertheless, inefficiencies in prior processing stages result in the retention of residual impurities within the decobaltage solution, which negatively impacts the production yield of cobalt hydroxide . These impurities not only impede the decobaltage procedure but also lead to a deterioration in product quality , . The global demand for cobalt has been experiencing consistent annual growth of around 4%, largely fueled by its essential role in rechargeable batteries, superalloys, and key sectors such as defense and aerospace. In response to this escalating demand, our research initiative investigates cobalt sourced from the Democratic Republic of the Congo (DRC) . The study, titled "Modeling of Cobalt Precipitation Yield, Impurities, and Magnesia from a Solvent Extraction Bleed Solution in the Copper Circuit of a Cupro-Cobalt Ore," aims to enhance production efficiency and refine purity levels in cobalt extraction and processing. This study focuses on enhancing metallurgical processes, particularly considering the growing industrial and technological demand for cobalt. The research objective is to maximize cobalt precipitation yield while effectively eliminating impurities such as magnesium. To achieve this, a mathematical and graphical model is developed using Minitab 18 software, serving as an analytical framework to systematically assess the impact of critical process variables on the target response. Through advanced statistical analysis, the study aims to elucidate key parameter interactions and their influence on process outcomes, thereby supporting data-informed optimization strategies. The findings are expected to enhance process efficiency and yield, contributing to advancements in metallurgical extraction and refinement techniques.
2. Research methods and principles
2.1. Materiel and reagent
The sample used in our study comes from the copper decantation at the Kwatebala plant of Tenke Fungurume Mining in the Democratic Republic of Congo (DRC). A series of characterizations were carried out on the 30-liter batch taken and on the process water.
The chemical analysis, the results of which are reported in Table 1 and Figure 2, was carried out by inductively coupled plasma optical emission spectrometry (ICP-OES) with an Optima 8300 plasma torch for the analysis of copper, cobalt, iron, magnesium, and aluminum.
The following reagents were used for the preparation of magnesium hydroxide as a precipitating agent including:
- Magnesia (MgO) in solid form (NEELKANTH).
- Water (H2O) in liquid form.
2.2. Experimental procedure
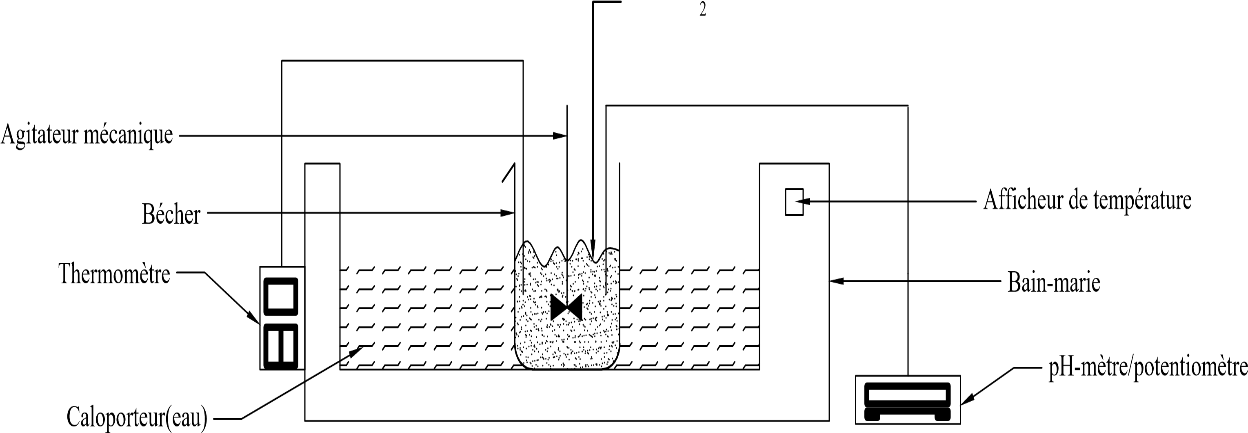
Figure 1 - Assembly for precipitation testing
3. Main results
3.1. Chemical analysis
3.1.1. Sample
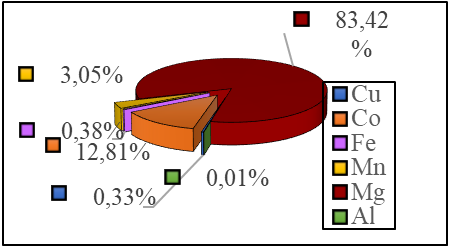
Figure 2 - Sample Composition
The chemical composition of water is given in the table 1 below. Which shows that the pH of the water used to prepare magnesium hydroxide is close to neutrality.
Table 1 - Chemical analysis of process water
Elements | ppm |
Al | 0.22 |
Ca | 410.17 |
Co | 16.69 |
Cu | 3.21 |
Fe | 0.06 |
Mg | 5118.4 |
Mn | 18.46 |
Si | 7.91 |
Zn | 0.03 |
pH | 7.35 |
3.2. Precipitation test
Based on the results from table i in the annexes, we observe that precipitation did indeed occur, as the residual concentrations of the elements are lower than the initial concentrations for the various tests conducted.
The examination of Table II in the annexes shows that we have a precipitation yield of 54.9% in cobalt (element to be valorized) in test number 2 with a consumption of 4 ml of magnesia which turns out to be the maximum consumption. This can be explained by the fact that the more magnesia is consumed, the more cobalt precipitates. Regarding the precipitation of the different metallic elements during the 20 tests carried out, we observe that the precipitation yields of the metals are dispersed on a scale ranging from 0 to 100%. Furthermore, the consumption of magnesia varied from 0.1 to 4 ml. Operating conditions kept constant: agitation speed at 500 rpm and a time of 4 hours.
Table 2 - Chemical characterization of 20 samples from precipitation trials
Tests | T° | %MgO | pH | Cu (%) | Co (%) | Fe (%) | Mn (%) | Mg (%) | Al (%) | Mg(OH)2 consumption (ml) |
1 | 40 | 15 | 7,55 | 80,392 | 25,752 | 100,000 | 0,000 | 12,209 | 0,000 | 0,800 |
2 | 40 | 15 | 8,3 | 1,961 | 54,910 | 49,153 | 30,672 | 10,732 | 0,000 | 4,000 |
3 | 45 | 17 | 8 | 68,627 | 42,535 | 96,610 | 21,008 | 3,816 | 50,000 | 3,500 |
4 | 48,4 | 15 | 7,55 | 60,784 | 10,822 | 83,051 | 15,966 | 22,202 | 0,000 | 0,200 |
5 | 40 | 15 | 6,8 | 1,961 | 15,531 | 69,492 | 15,966 | 4,608 | 0,000 | 0,200 |
6 | 40 | 15 | 7,55 | 66,667 | 27,856 | 100,000 | 0,420 | 13,501 | 0,000 | 0,750 |
7 | 45 | 13 | 8 | 60,784 | 23,747 | 98,305 | 9,034 | 13,432 | 50,000 | 3,000 |
8 | 40 | 11,64 | 7.55 | 98,039 | 20,842 | 66,102 | 20,168 | 5,354 | 50,000 | 0,300 |
9 | 40 | 15 | 7,55 | 56,863 | 21,092 | 100,000 | 2,521 | 11,270 | 0,000 | 1,500 |
10 | 45 | 13 | 7,1 | 80,392 | 15,531 | 93,220 | 4,202 | 4,600 | 50,000 | 0,800 |
11 | 35 | 13 | 7,1 | 80,392 | 16,733 | 96,610 | 7,143 | 8,293 | 0,000 | 0,900 |
12 | 45 | 17 | 7,1 | 76,471 | 17,435 | 86,441 | 5,252 | 3,300 | 50,000 | 0,800 |
13 | 40 | 15 | 7,55 | 25,490 | 23,146 | 97,797 | 1,471 | 12,216 | 0,000 | 1,500 |
14 | 35 | 17 | 8 | 74,510 | 45,441 | 98,305 | 20,798 | 8,839 | 0,000 | 3,000 |
15 | 40 | 18,4 | 7,55 | 50,980 | 48,998 | 84,746 | 3,361 | 0,846 | 0,000 | 0,100 |
16 | 40 | 15 | 7,55 | 80,392 | 27,204 | 100,000 | 0,000 | 14,993 | 0,000 | 1,000 |
17 | 31,6 | 15 | 7,55 | 21,569 | 15,832 | 66,102 | 20,168 | 1,816 | 50,000 | 0,200 |
18 | 35 | 13 | 8 | 80,392 | 25,852 | 98,305 | 18,067 | 2,669 | 0,000 | 4,000 |
19 | 35 | 17 | 7,1 | 60,784 | 11,824 | 66,102 | 13,866 | 6,947 | 50,000 | 0,100 |
20 | 40 | 15 | 7,55 | 49,020 | 21,042 | 100,000 | 0,210 | 11,539 | 0,000 | 0,800 |
Table 3 - Metal precipitation yields and magnesia consumption over 20 trials
Tests | T° | %solid MgO | pH | Sample's code | Cu (g/L) | Co (g/L) | Fe (g/L) | Mn (g/L) | Mg (g/L) | Al (g/L) |
1 | 40 | 15 | 7,55 | DCo1 | 0,010 | 1,482 | 0,000 | 0,476 | 11,412 | 0,002 |
2 | 40 | 15 | 8,3 | DCo122y | 0,050 | 0,900 | 0,030 | 0,330 | 11,604 | 0,002 |
3 | 45 | 17 | 8 | DCo13y | 0,016 | 1,147 | 0,002 | 0,376 | 12,503 | 0,001 |
4 | 48,4 | 15 | 7,55 | DCo17 | 0,020 | 1,780 | 0,010 | 0,400 | 10,113 | 0,002 |
5 | 40 | 15 | 6,8 | DCo13 | 0,050 | 1,686 | 0,018 | 0,400 | 12,400 | 0,002 |
6 | 40 | 15 | 7,55 | DCo2 | 0,017 | 1,440 | 0,000 | 0,474 | 11,244 | 0,002 |
7 | 45 | 13 | 8 | Dco12y | 0,020 | 1,522 | 0,001 | 0,433 | 11,253 | 0,001 |
8 | 40 | 11,64 | 7.55 | DCo19 | 0,001 | 1,580 | 0,020 | 0,380 | 12,303 | 0,001 |
9 | 40 | 15 | 7,55 | DCo3 | 0,022 | 1,575 | 0,000 | 0,464 | 11,534 | 0,002 |
10 | 45 | 13 | 7,1 | DCo7 | 0,010 | 1,686 | 0,004 | 0,456 | 12,401 | 0,001 |
11 | 35 | 13 | 7,1 | DCo8 | 0,010 | 1,662 | 0,002 | 0,442 | 11,921 | 0,002 |
12 | 45 | 17 | 7,1 | DCo9 | 0,012 | 1,648 | 0,008 | 0,451 | 12,570 | 0,001 |
13 | 40 | 15 | 7,55 | DCo6 | 0,038 | 1,534 | 0,001 | 0,469 | 11,411 | 0,002 |
14 | 35 | 17 | 8 | DCo18x | 0,013 | 1,089 | 0,001 | 0,377 | 11,850 | 0,002 |
15 | 40 | 18,4 | 7,55 | DCo14 | 0,025 | 1,018 | 0,009 | 0,460 | 12,889 | 0,002 |
16 | 40 | 15 | 7,55 | DCo5 | 0,010 | 1,453 | 0,000 | 0,476 | 11,050 | 0,002 |
17 | 31,6 | 15 | 7,55 | DCo18 | 0,040 | 1,680 | 0,020 | 0,380 | 12,763 | 0,001 |
18 | 35 | 13 | 8 | DCo12x | 0,010 | 1,480 | 0,001 | 0,390 | 12,652 | 0,002 |
19 | 35 | 17 | 7,1 | DCo15 | 0,020 | 1,760 | 0,020 | 0,410 | 12,096 | 0,001 |
20 | 40 | 15 | 7,55 | DCo4 | 0,026 | 1,576 | 0,000 | 0,475 | 11,499 | 0,002 |
3.3. Mathematical modeling graph results
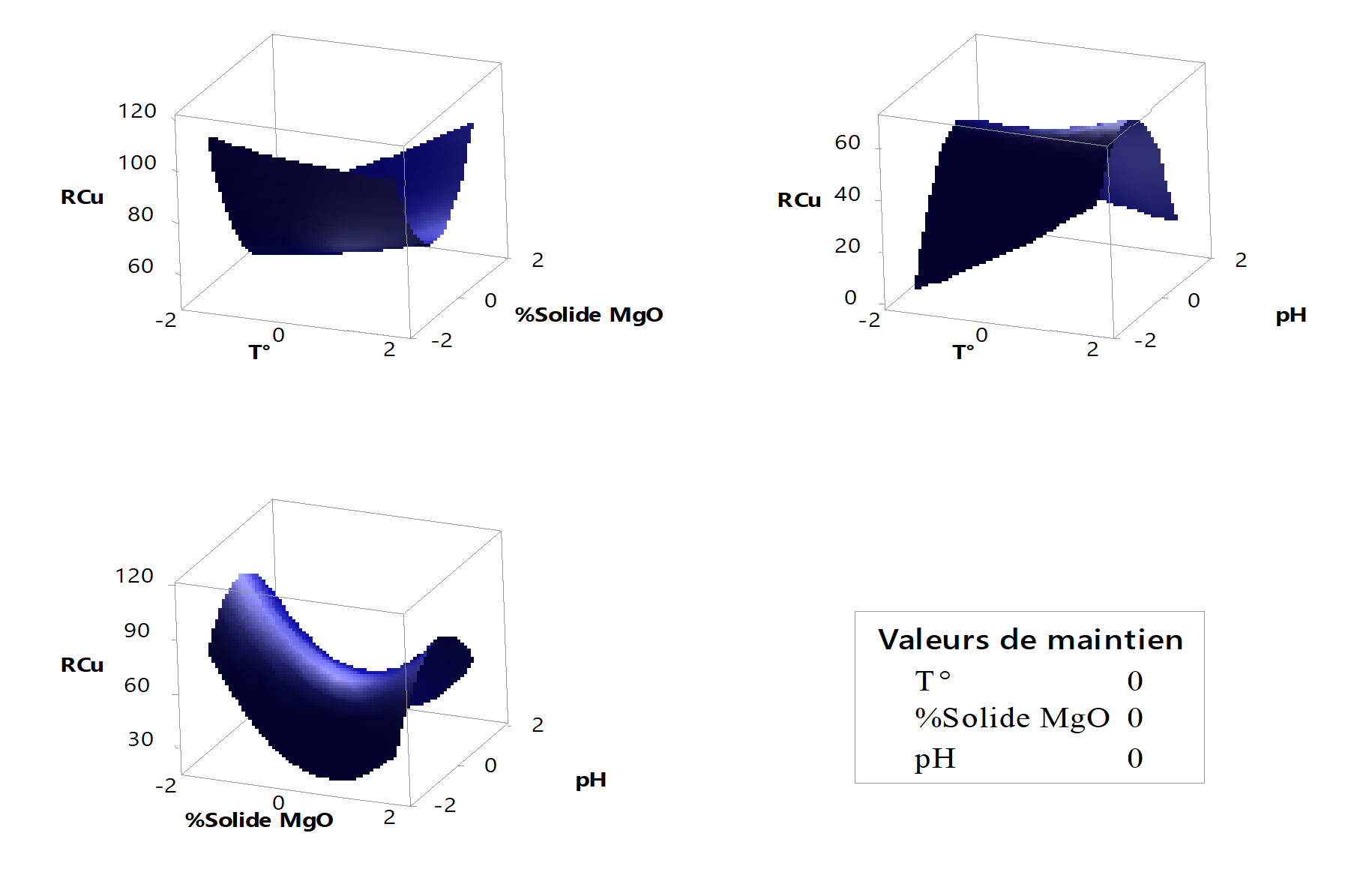
Figure 3 - Surface diagrams of copper precipitation yield
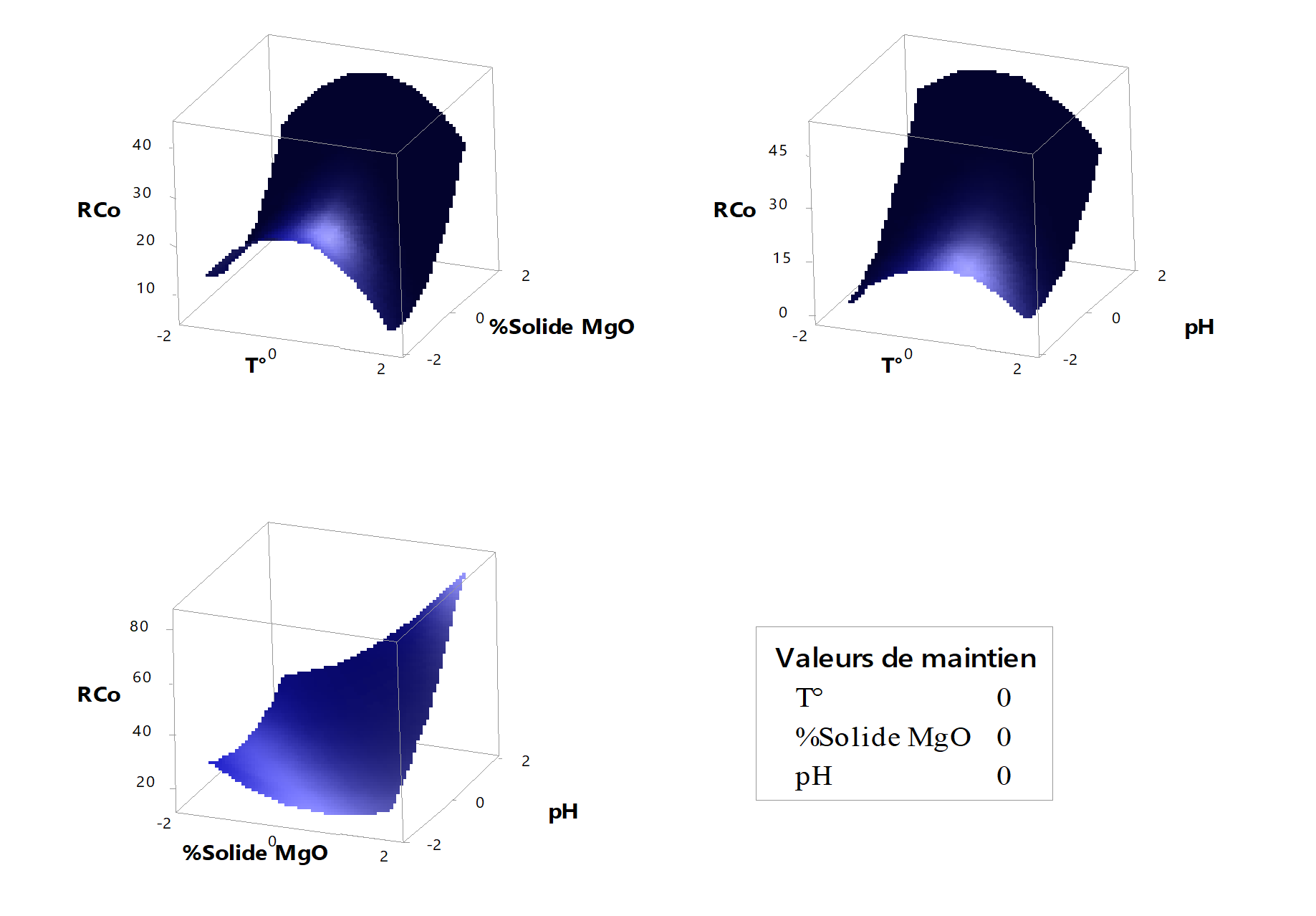
Figure 4 - Surface diagrams of cobalt precipitation yield

Figure 5 - Surface diagrams of Iron precipitation yield

Figure 6 - Surface diagrams of Manganese precipitation yield
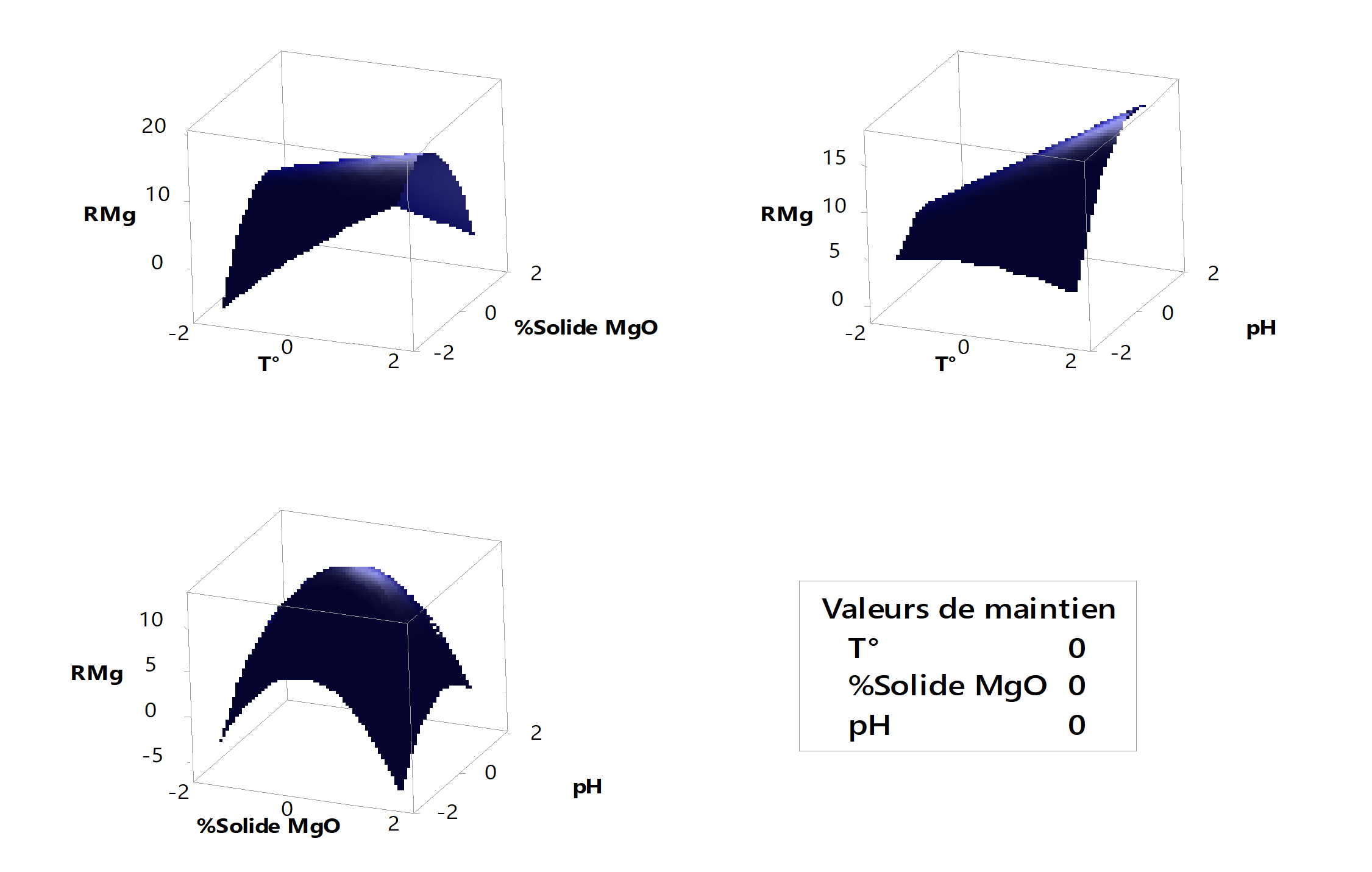
Figure 7 - Surface diagrams of magnesium precipitation yield
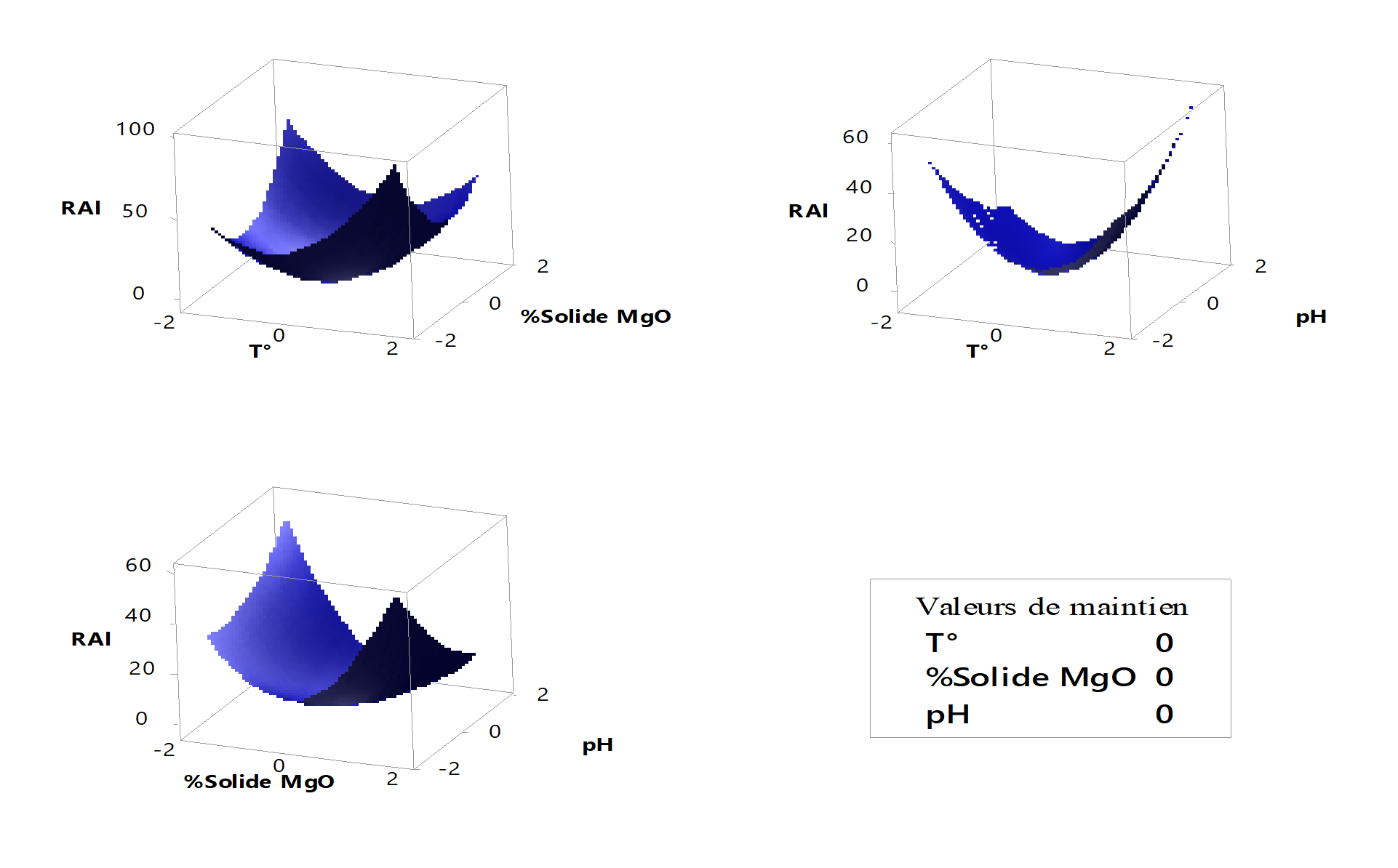
Figure 8 - Surface diagrams of aluminum precipitation yield
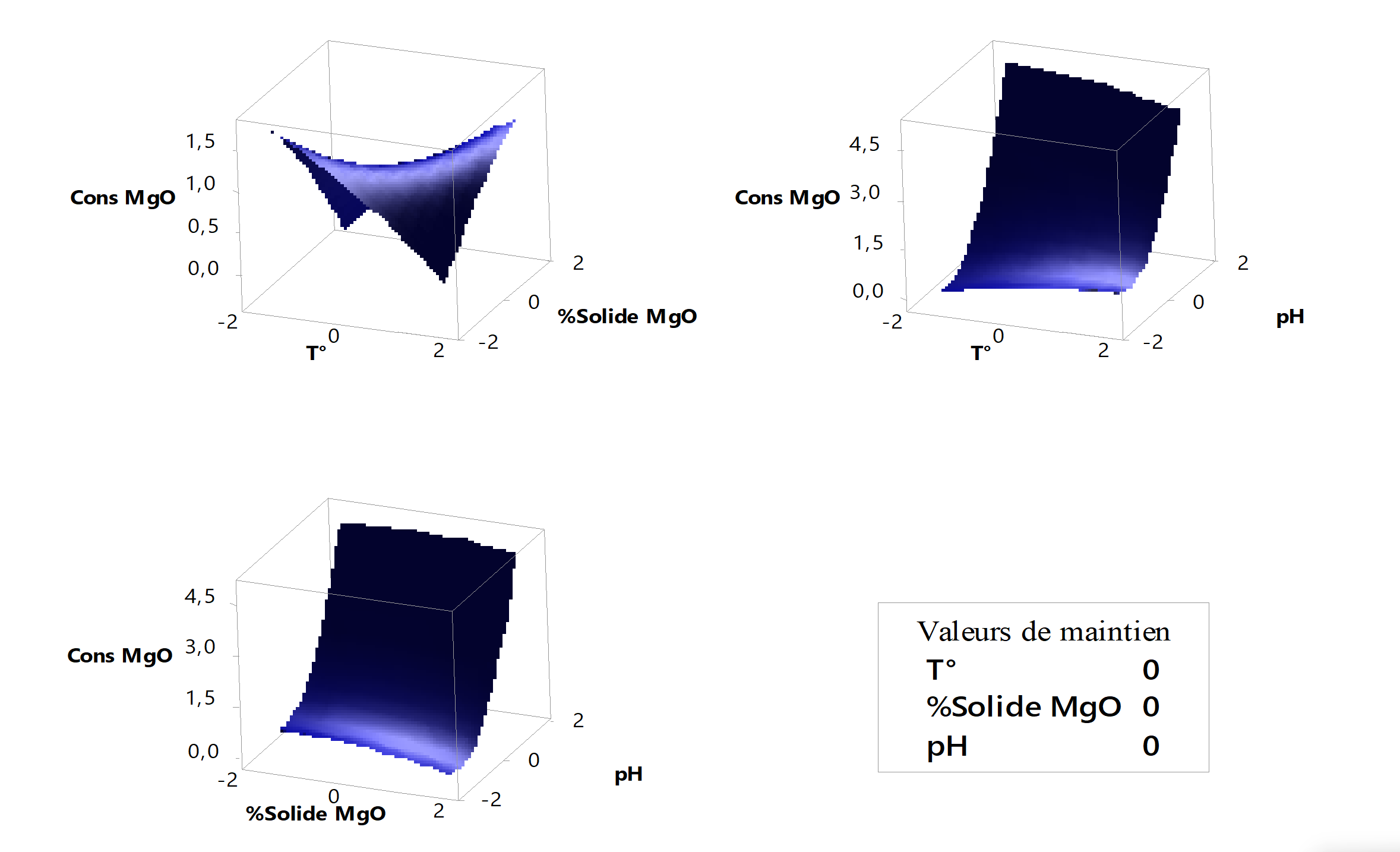
Figure 9 - Surface diagrams of magnesia consumption
4. Discussion
4.1. Sample and process water
Copper comprises the majority of the composition at 83.42%, while cobalt, a valuable metal, constitutes a secondary proportion of 12.81%. The chemical composition of the water is presented in Table 1, which indicates that the pH of the water used in the preparation of magnesium hydroxide is near neutral.
4.2. Copper precipitation yield
Figure 3 presents the copper precipitation yield as a function of various factors, accounting for the synergistic effects of temperature and the percentage of magnesia solids (%solid). The minimum yield occurs at %solid = 0 and temperature = -1.68. Furthermore, when examining the interaction between pH and temperature, the minimum yield is observed at pH = -1.68 and temperature = -1.68. Similarly, the combined effects of pH and %solid reveal that the minimum yield is attained at pH = -1.68 and %solid = 0.
4.3. Cobalt precipitation yield
Figure 4 illustrates cobalt precipitation as a function of the examined parameters. The results demonstrate that, when accounting for all synergistic effects among the factors, increasing the pH to approximately 1.68 maximizes cobalt precipitation yield. Conversely, elevating temperature reduces cobalt recovery yield, which aligns with its negative coefficient in the mathematical model. These findings are consistent with prior research by Djoudi et al
. Additionally, increasing the magnesia solid percentage to around 1.68 further enhances cobalt recovery yield.4.4. Iron precipitation yield
Figure 5 illustrates the surface diagram depicting iron precipitation behavior. The analysis reveals that an acidic pH of -1.68, in conjunction with a solid percentage range of 0 to 1.68, promotes the minimization of iron precipitation efficiency. Furthermore, the interaction between pH (0 to -1.68) and temperature similarly contributes to reduced iron precipitation performance.
4.5. Manganese precipitation yield
Figure 6 presents the surface diagrams depicting manganese precipitation, revealing that the minimum precipitation yield occurs near the center of the domain, approaching values of zero across all considered factors.
4.6. Magnesium precipitation yield
Figure 7 shows that the minimal precipitation yield of magnesium is around -1.68 for the interaction of magnesia solid % and temperature. Considering the synergistic effects of temperature and pH, it is observed that the minimal precipitation yield of magnesium is at a value of 1.68 for temperature and -1.68 for pH. Considering the effects of magnesia solid % and pH, it is found that the minimal yield is located at respective values of 1.68 and -1.68.
4.7. Aluminum precipitation yield
Based on the surface diagrams that reflect the precipitation yield of aluminum, it can be observed that the minimum precipitation yield of aluminum is located at the center of the domain, i.e. at close values to for all factor interactions considered in our study.
4.8. Magnesia consumption
Figure 9 translates magnesia consumption as a function of our factors. The higher we want to work at extreme values of the factors (1.68), the more magnesia we consume. Regarding the analysis of the interaction between temperature and solid percentage, magnesia consumption is high when approaching values close to -1.68. According to the analysis, as the temperature increases, more solutes (precipitating agents) are needed to saturate the solution.
5. Conclusion
The primary objective of this study was to develop a mathematical and graphical decision-making tool to optimize the precipitation yield of cobalt while minimizing the co-precipitation of impurities (Cu, Fe, Mn, Mg, and Al) and reducing magnesia consumption. The proposed precipitation scheme involves a series of operations, including precipitation and filtration, to achieve efficient separation. Optimal operating conditions were determined as follows: an agitation speed of 500 rpm, a reaction time of 4 hours, a pH of 8.3, a temperature of 40°C, and a solid percentage of 15%. Under these conditions, a cobalt precipitation yield of 54.910% was achieved, with a magnesia consumption of 4 mL. The graphical analysis revealed that, when considering the linear effects of the studied factors, the precipitation yields of aluminum, magnesium, and iron were most significantly influenced by temperature, whereas copper precipitation was also predominantly affected by temperature. In contrast, cobalt precipitation yield was more strongly dependent on pH and solid percentage. Additionally, it was observed that extreme factor values (1.68) resulted in significantly higher magnesia consumption. This tool provides a systematic approach for identifying optimal precipitation conditions, thereby enhancing process efficiency while minimizing reagent usage and impurity co-precipitation.
