Development and research of convolutional neural network models in similar image search problems

В настоящее время задача определения местоположения на основе спутниковых снимков является актуальной задачей, позволяющей осуществлять навигацию без использования глобальных навигационных систем. Решение данной задачи невозможно без алгоритма сопоставления аэрофотоснимка и некоторой карты местности. В данной работе рассматривается решение задачи нахождения места съемки с использованием алгоритмов поиска по содержанию. В качестве исходных данных имеется поисковая коллекция изображений, которая представляет собой спутниковое изображение местности подстилающей поверхности, разбитое на фрагменты. Необходимо определить где в текущий момент времени осуществляется съемка на основе видеоряда съемки на небольшой высоте. Задача усложняется из-за значительных различий в условиях съемки: время суток, сезон, облачность, угол наклона сенсора и масштаб съемки. Существуют подходы, которые на основе особых точек и оптического потока определяют относительное перемещение, однако при больших расстояниях есть вероятность накопления значительной ошибки.

В данной работе рассматривается решение описанной выше задачи с использованием неглубоких свёрточных сетей. Предлагается сжимать пространство признаков изображения до некоторого вектора, фиксированного размера, на основе которого в дальнейшем становится возможно определить расположение места съёмки. Для этого необходимо осуществить обучение нейронной сети на различных парах изображений, подверженных проективным преобразованиям. В ходе работы были исследованы различные архитектуры свёрточных сетей, а также предложено собственное решение, где за основу взята модель VGG (Visual Geometry Group) — архитектура сверточных нейронных сетей, разработанная для задач классификации изображений

Постановка задачи. Необходимо разработать алгоритм обучения нейронной сети, модернизировать модель VGG16 применительно к задаче поиска изображений.

На рисунке 1 приведена модель свёрточной нейронной сети VGG16. Данная сеть изначально предполагается для задачи классификации, однако может быть модернизирована для поиска изображений по содержанию. Рассмотрим архитектуру модели подробнее.

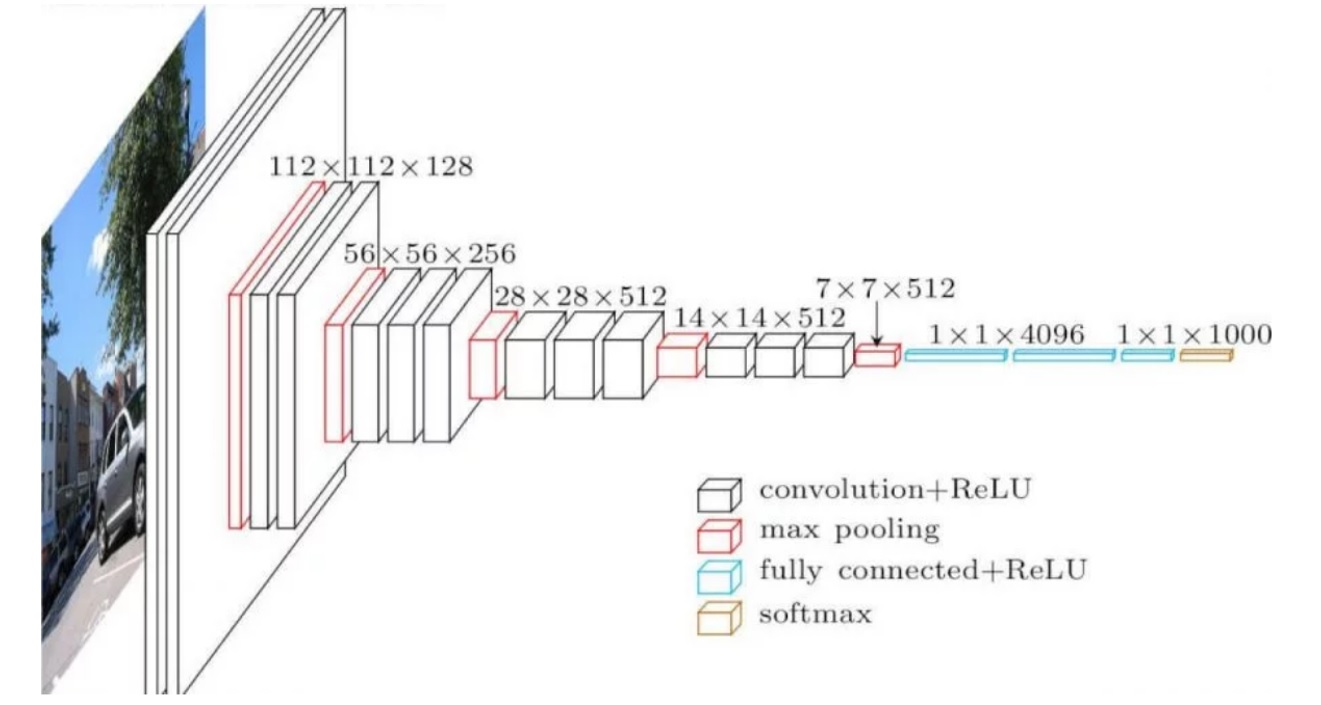
Рисунок 1 - Модель сверточной нейронной сети VGG16

DOI:10.60797/IRJ.2025.156.22.1

Основные характеристики VGG16:

- Глубина сети: 16 слоев, которые обучаются (включая 13 сверточных слоев и 3 полносвязных слоя). Число «16» в названии указывает на количество обучаемых слоев.

- Свёрточные слои: применяются свёрточные слои с небольшими фильтрами размером 3x3, что позволяет сети захватывать более сложные паттерны и детали в изображениях. Слои организованы в блоки, где после нескольких сверточных слоев следует слой подвыборки (max pooling).

- Max Pooling: слои подвыборки (обычно 2x2) используются для уменьшения пространственного разрешения и снижения вычислительной сложности, а также для извлечения наиболее значимых признаков.

- Активация: в качестве функции активации используется ReLU (Rectified Linear Unit), что помогает ускорить обучение и улучшить производительность сети.

- Полносвязные слои: в конце сети находятся три полносвязных слоя, где последний слой использует функцию активации softmax для классификации.

- Параметры: VGG16 имеет около 138 миллионов параметров, что делает ее вычислительно сложной, но при этом она демонстрирует высокую точность в различных задачах.

Для обучения такой сети требуется ее расширения до сиамской архитектуры, где на вход подаются два изображения, а на выходе формируется единственное значение — величина подобности изображений. На рисунке 2 представлена модель вычисления сходства с использованием сиамских сетей. 

Принцип работы сиамский сетей заключается в использовании двух идентичных сетей для пары изображений, на выходном слое формируется вектор признаков

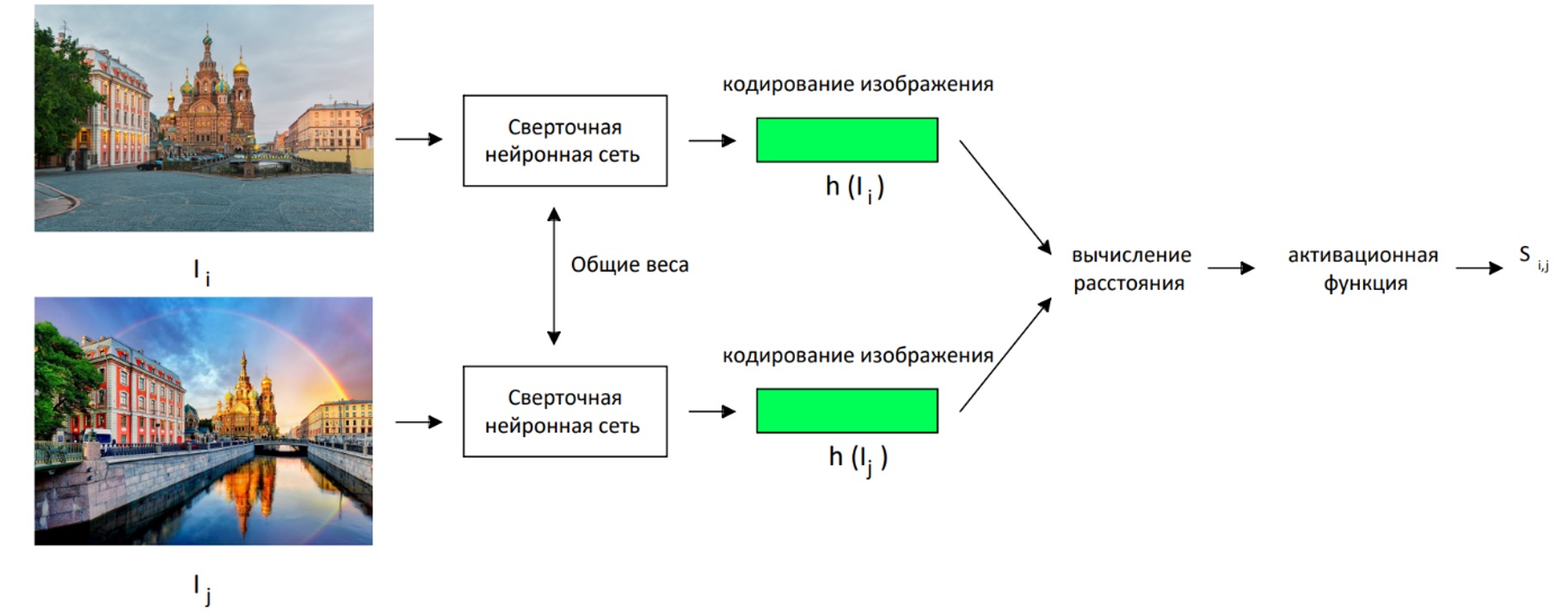
Рисунок 2 - Модель вычисления сходства с использованием сиамских сетей

DOI:10.60797/IRJ.2025.156.22.2

Косинусное сходство рассчитывается по формуле (1) и представляет собой меру, используемую для оценки схожести между двумя векторами в пространстве, основанную на косинусе угла между ними. В контексте визуального поиска и обработки изображений, косинусное сходство часто применяется для сравнения векторных представлений (например, признаков) изображений

[5]

.

Косинусное сходство между двумя векторами A и B можно вычислить по следующей формуле:

(1)

где  — скалярное произведение векторов A и B,  – норма (длина) вектора A, вычисляемая как ,  – итерируемая переменная,  — размерность вектора,  — норма (длина) вектора B, вычисляемая аналогично.

Значение косинусного сходства варьируется от -1 до 1:

1. Значение 1 означает, что векторы идентичны (максимальная схожесть).

2. Значение 0 означает, что векторы ортогональны (нет схожести).

3. Значение -1 указывает на противоположные направления (в контексте поиска похожих изображений это обычно не имеет смысла, так как векторы признаков обычно не имеют отрицательных значений).

В поиске похожих изображений косинусное сходство используется для сравнения векторных представлений изображений, полученных, например, с помощью сверточных нейронных сетей

Евклидово расстояние — это мера, используемая для определения «дистанции» между двумя точками в пространстве. В контексте визуального поиска и обработки изображений, евклидово расстояние может применяться при сравнении векторных представлений изображений

Когда изображения преобразуются в векторные представления (например, с помощью сверточных нейронных сетей), Евклидово расстояние может использоваться для измерения различий между этими векторами. Чем меньше Евклидово расстояние между векторами двух изображений, тем более похожими они считаются.

(2)

где  и  — компоненты векторов A и B соответственно,  – количество измерений (или размерность векторов).

Выбор свёрточной архитектуры, а также количество характеристик в векторе сильно зависят от формата входных данных и обучающей выборке. Поэтому для данной задачи были исследованы как существующие модели ImageNet, так и разработанные в ходе данного исследования, на основе VGG16

Выбор метрики оценки расстояния между векторами признаков обуславливается тем, что косинусное сходство фокусируется на направлении векторов, что позволяет лучше оценивать, насколько два документа схожи по содержанию, независимо от их абсолютной величины. Выбор косинусного сходства в задачах поиска по содержанию обусловлен его способностью более точно отражать семантическое сходство между векторами. 

В ходе обучения сети было выявлено, что существующие модели с большим количеством весов склонны к переобучению, в то время как неглубокие модели демонстрируют более высокие показатели точности при фиксированном количестве эпох (количество полных проходов через обучающий набор данных). В таблице 1 приведены рассматриваемые модели нейронной сети, время обучения в мс, количество весов у указанных моделей, а также ошибка, вычисленная с использованием СКО.

Исходя из данных, полученных в таблице 1 можно сделать вывод, что при существенном уменьшении количества весов (в 10 раз по сравнению с MobileNet v2) ошибка (СКО) ниже. 

В предлагаемой модели акцент был сделан на замене функции активации (ELU вместо ReLU), что позволило избавиться от проблемы «умирающих» нейронов, а также снизило количество свёрток на слоях сети.

В качестве последнего слоя свёрточной сети располагался вектор характеристик изображения. На последнем слое свёрточной нейронной сети VGG16 (рисунок 1) получаем 1000 характеристик, которые представляются в виде вектора. На таблице 2 представлена архитектура предлагаемой нейронной сети. 

Данная архитектура относится к разряду классических свёрточных сетей. Размер входного изображения — 256x256 пикселей с 3 каналами (RGB). Модель состоит из нескольких свёрточных слоёв, которые применяют фильтры к входным данным для извлечения признаков. Каждый свёрточный слой использует активацию ELU (Exponential Linear Unit), которая помогает модели быстрее сходиться и избегать проблемы «умирающих нейронов». После нескольких свёрточных слоёв применяется операция MaxPooling, которая уменьшает размерность карт признаков, сохраняя наиболее важные признаки. Это помогает снизить вычислительную сложность и предотвратить переобучение. После последнего слоя MaxPooling2D, данные выравниваются в одномерный вектор, который представляет собой вектор признаков изображения.

Размерность данных постепенно уменьшается от 256x256 до 1x1, что типично для CNN. Это достигается за счёт комбинации свёрточных слоёв и слоёв подвыборки. Количество фильтров (каналов) в свёрточных слоях варьируется от 128 на начальных слоях (поскольку наибольшую ценность в аэрофотосъёмках имеет именно высокочастотная составляющая) до 16 и 64 на более глубоких слоях, что позволяет модели извлекать как общие, так и более специфические признаки. Общее количество обучаемых параметров модели составляет 395 872. Это относительно небольшое количество параметров для CNN, что делает модель менее склонной к переобучению и более подходящей для задач, где доступно ограниченное количество данных.

В целом, данная модель представляет собой компактную и эффективную свёрточную нейронную сеть, которая подходит для задач извлечения признаков аэрокосмических изображений. Она хорошо сбалансирована по количеству параметров и может быть использована в условиях ограниченных вычислительных ресурсов.

Было проведено исследование, результаты которого представлены на рисунке 3, как количество характеристик влияет на вероятность обнаружения пары.

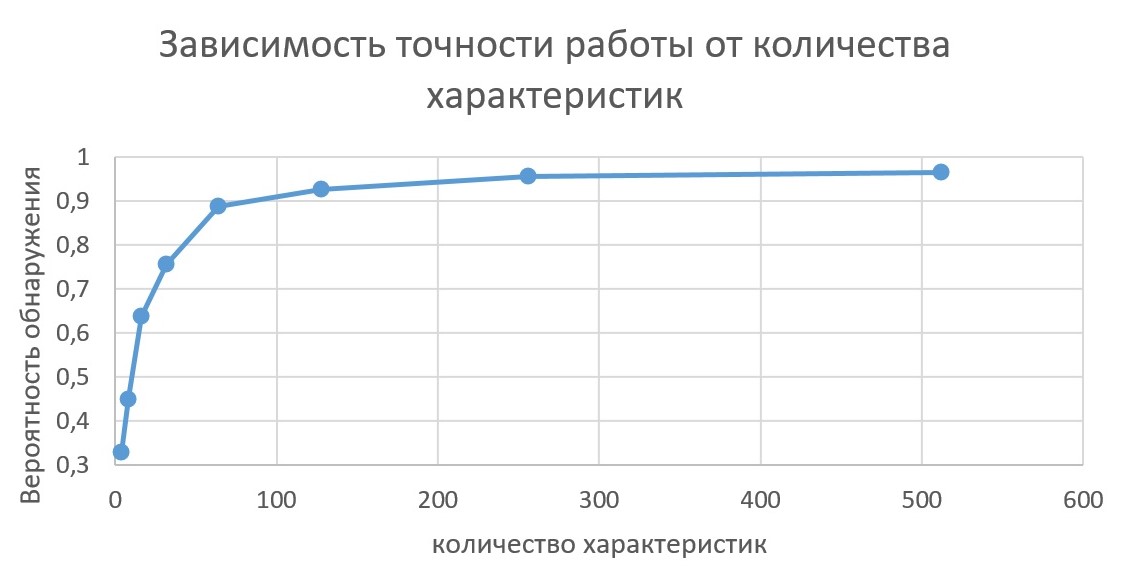
Рисунок 3 - Зависимость вероятности обнаружения пары изображений от количества характеристик

DOI:10.60797/IRJ.2025.156.22.5

Исходя из рисунка 3, было получено, что при значениях 128, 256, 512 разница в вероятности корректного обнаружения находится ниже, чем погрешность вычислений, возникающая из-за особенности алгоритма обучения. Таким образом, разработанная модель с фиксированным количеством характеристик равным 128 является наиболее оптимальным с точки зрения вероятности обнаружения пары изображений для решения рассматриваемой задачи.

Также ниже представлены результаты экспериментальных исследований пар изображений. Приведены 3 примера пар и значения показателей их схожести.

Рисунок 4 - Пара изображений с величиной сходства - 0,63

Примечание: различный сюжет

DOI:10.60797/IRJ.2025.156.22.6

Рисунок 5 - Пара изображений с величиной сходства - 0,98

Примечание: идентичный сюжет

DOI:10.60797/IRJ.2025.156.22.7

Рисунок 6 - Пара изображений с величиной сходства - 0,93

Примечание: идентичный сюжет

DOI:10.60797/IRJ.2025.156.22.8

В данной работе было проведено исследование существующих свёрточных моделей нейронных сетей для решения задачи поиска похожих аэрокосмических изображений. Экспериментальная проверка на основе разработанного набора данных показала, что существующие архитектуры не являются оптимальными для данной задачи. Была предложена адаптация архитектуры VGG16 для решения поставленной задачи. Предлагаемая модель нейронной сети позволила более эффективно с точки зрения вероятности обнаружения пар изображений выделить значимые характеристики аэрофотоснимков, в сравнении с существующими моделями, при этом обладая в разы меньшей вычислительной сложностью. Также на предложенной модели было исследовано определение оптимального количества числовых характеристик изображения. При существенном уменьшении количества весов (в 10 раз по сравнению с MobileNet v2) ошибка (СКО) ниже на ≈ 0.6. Были проведены исследования на значениях, от 4 до 512. Было определено, что при увеличении числа характеристик свыше 128 точность практически не изменяется.