A COMPARISON OF SOFTMAX AND SIGMOID ACTIVATION FUNCTIONS IN THE CONTEXT OF MULTI-CLASS OBJECT RECOGNITION CLASSIFICATION
A COMPARISON OF SOFTMAX AND SIGMOID ACTIVATION FUNCTIONS IN THE CONTEXT OF MULTI-CLASS OBJECT RECOGNITION CLASSIFICATION
Abstract
This article studies an important problem related to the application of softmax function in multiclass object classification tasks. The paper describes the structure and operation of an artificial neuron, as well as the principle of activation functions on the example of an adder. In particular, it considers the situation when input data does not correspond to any of the classes in the dataset, which can lead to incorrect model outputs. This calls into question the accuracy of classification and requires systematic control and handling of such cases. This work proposes an alternative approach using a sigmoidal activation function and setting a threshold value to determine whether an object belongs to the classification classes. The approach allows for a more accurate evaluation of classification results and avoiding false conclusions.
1. Введение
В создании искусственных нейронных сетей одним из ключевых аспектов является выбор функции активации. Эта функция определяет поведение нейрона и формирует выходной сигнал в зависимости от входных данных. Среди различных функций активации функции softmax и сигмоиды играют особенно важную роль в задачах классификации.
В данном исследовании мы сосредоточимся на проблеме, которая возникает при использовании функции softmax в задачах многоклассовой классификации, когда входные данные не соответствуют ни одному из классов в наборе данных. Это может привести к неправильным выводам и потребности в контроле таких ситуаций.
Далее мы предложим альтернативный подход, в котором используется функция активации сигмоиды и устанавливается пороговое значение для определения принадлежности объекта к классам классификации. Этот подход позволяет улучшить точность классификации и избежать ложных результатов.
2. Основы функций активации и математические уравнения функции softmax и сигмоиды
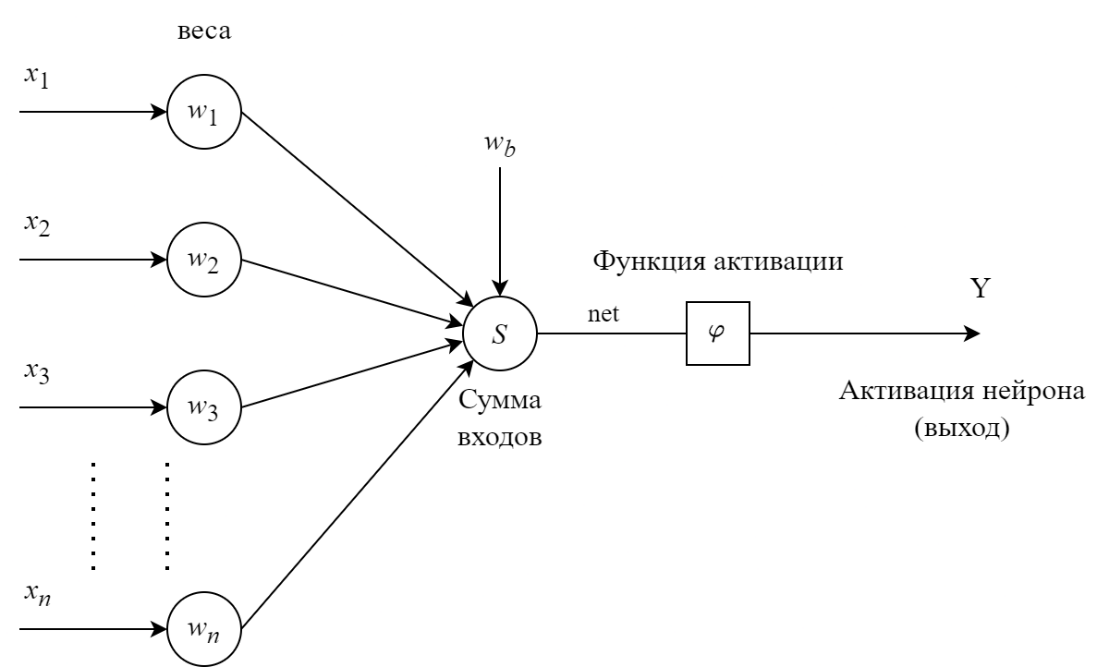
Рисунок 1 - Структурная схема искусственного нейрона
;
где: xi – выходной сигнал i-го нейрона;
wi – вес i-го нейрона;
n – количество нейронов, входящих в обрабатываемый нейрон.
Сумматор генерирует выходной сигнал net, который затем преобразуется функцией активации. Формула для вычисления net:
;
где wb – сигнал смещения (bias), отображающий функцию предельного значения.
Функция активации f(S) обрабатывает выходной сигнал сумматора net и формирует нейронный сигнал выхода Y.
В задачах распознавания объектов на изображениях доминируют сверточные нейронные сети (СНС). СНС состоит из сверточных слоев и слоев пулинга, последовательно соединенных друг с другом. Далее эти слои подключаются к полностью связанному слою, который формирует выходные данные. Перед формированием выходных данных используются функции активации. Наиболее распространенные функции активации: Функция softmax и сигмоидальная функция.
3. Сигмоидальная функция
Сигмоидальная функция активации – это нелинейная функция, которая преобразует входное значение в диапазоне от отрицательной бесконечности до положительной бесконечности в значение от 0 до 1. Эта функция активации часто используется в нейронных сетях для задач бинарной классификации
.Сигмоидальная функция активации представлена формулой :
.
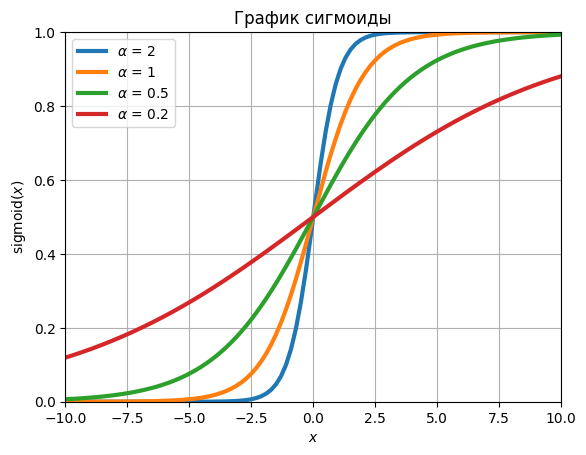
Рисунок 2 - График сигмоидальной функции активации
4. Функция Softmax
Функция Softmax используется для преобразования вектора значений в вероятностное распределение, которое суммируется до 1
. Она особенно полезна в многоклассовой классификации, где необходимо определить вероятности для каждого класса.Формула функции Softmax выглядит следующим образом:
;
где zi – это элемент входного вектора, а k – это общее число элементов в векторе.
![График функции softmax, соответствующий входному вектору z = [1, 2, 3, 4, 1, 2, 3]](/media/images/2024-06-13/a0239a29-24d1-487f-89ce-22753b5be920.png)
Рисунок 3 - График функции softmax, соответствующий входному вектору z = [1, 2, 3, 4, 1, 2, 3]
5. Проблема для задачи многоклассовой классификации
Как упоминалось выше, функция softmax широко используется в задачах многоклассовой классификации. Из-за природы функции softmax все выходные значения будут представлять собой вероятности каждого класса. Независимо от того, какой класс имеет наибольшее значение вероятности, система предсказывает, что входное изображение принадлежит именно этому классу.
Однако, при рассмотрении конкретного примера, такого как классификация знаковых зданий города Москвы
, в которой набор данных включает 13 выходных классов, соответствующих 13 зданиям в городе, возникает проблема интерпретации результатов. Система классификации может точно предсказать здание, если входные данные изображения принадлежат одному из классов набора данных. Однако в случае если входные данные не соответствуют ни одному из классов набора данных (например, изображения реки, горы, человека, странного здания и т. д.), после прохождения через полносвязный слой с применением функции softmax, система все равно выдаст наибольшую вероятность определенного класса из набора, что может привести к ложным выводам и неправильной классификации. Данное явление требует системного контроля и обработки для предотвращения неоправданных результатов.
Рисунок 4 - Образец изображения храма Спаса на Крови
[[4.2251e-07 8.3223e-06 1.1393e-05 1.3564e-05 2.9395e-06 0.00018633 0.00048449 1.2825e-05 2.5042e-08 4.021e-07 0.99911 0.0001692 2.4293e-09]]index max: 10label predict: St. Basils CathedralИз результатов видно, что модель, использующая функцию активации softmax, достигает очень высоких результатов (99,91%), поэтому нам очень сложно определить метки для изображений, которые не принадлежат ни к одному классу в наборе данных.
6. Решение
Чтобы решить эту проблему, мы применим функцию активации сигмовидной, а затем посмотрим на полученные результаты. Ниже приведены результаты модели, если к последнему слою применяется сигмовидная функция активации.
[[2.7557e-05 0.014681 9.0419e-05 0.0017351 0.0022757 0.00075092 0.00022904 6.3055e-06 0.00012885 2.1713e-05 0.31547 0.0082597 0.00029327]]index max: 10Таким образом, наибольшее значение в слоях классификации по-прежнему находится в 10-м слое (это Собор Василия Блаженного), но полученное значение значительно меньше (0,31547). Помните, что это число не является процентом вероятности для всех классификационных классов.
Поэтому мы можем установить пороговое значение, например 0,5. Если полученное максимальное значение больше 0,5, то мы можем предположить, что входное изображение принадлежит этому классу классификации, в противном случае мы можем заключить, что входное изображение не принадлежит ни одному классу классификации в наборе данных.
[[2.7557e-05 0.014681 9.0419e-05 0.0017351 0.0022757 0.00075092 0.00022904 6.3055e-06 0.00012885 2.1713e-05 0.31547 0.0082597 0.00029327]]index max: 10label predict: Unknown
Рисунок 5 - Изображение с контуром рамки обнаружения здания
7. Заключение
В данной статье мы рассмотрели основы функций активации и их математические уравнения, сфокусировавшись на функциях softmax и сигмоиды. Функция активации играет важную роль в построении и обучении искусственных нейронных сетей, определяя их функциональные возможности. Мы изучили структуру и работу искусственного нейрона, а также принцип действия функций активации на примере сумматора.
Сигмоидальная функция широко используется в задачах бинарной классификации, преобразуя входное значение в диапазон от 0 до 1. Функция softmax, в свою очередь, применяется в многоклассовой классификации, преобразуя вектор значений в вероятностное распределение.
Однако, рассматривая конкретную проблему многоклассовой классификации зданий в городе Москве, мы обнаружили, что использование функции softmax может привести к ложным результатам, особенно когда входные данные не соответствуют ни одному классу в наборе данных. Это ставит под сомнение точность классификации и требует системного контроля и обработки таких случаев.
В заключении мы предложили решение данной проблемы, заключающееся в применении функции активации сигмоиды и установлении порогового значения для определения принадлежности входного изображения к классам классификации. Этот подход позволяет более точно оценивать результаты классификации и избегать ложных выводов.
