ASPECTS OF THE IMPLEMENTATION OF THE FUZZY INFERENCE MECHANISM IN FUZZY SYSTEMS

ОСОБЕННОСТИ РЕАЛИЗАЦИИ МЕХАНИЗМА НЕЧЕТКОГО ЛОГИЧЕСКОГО ВЫВОДА В НЕЧЕТКИХ СИСТЕМАХ

Научная статья

Леденева Т.М.¹, Решетников А.Д.^2, *

¹ ORCID: 0000-0002-3944-2266;

² ORCID: 0000-0002-8217-3815;

^{1, 2} Воронежский государственный университет, Воронеж, Россия

* Корреспондирующий автор (reshetnikov.alex93[at]gmail.com)

Аннотация

Нечеткие системы используются для моделирования, анализа данных, прогнозирования, принятия решений, управления в различных предметных областях, в том числе, связанных с техническими приложениями. По сути, нечеткая система является универсальным аппроксиматором, причем известно, что любую сложную систему можно аппроксимировать нечеткой системой с любой заданной точностью, если подходящим образом подобрать функциональное представление нечетких логических связок, которые участвуют в модели. На данный момент сформировался ряд стандартных подходов, но на фоне развития разделов теории нечетких множеств и нечеткой логики, которые связаны с функциональным представлением нечетких операций (различные семейства треугольных норм и конорм и порожденные ими импликации, функции агрегирования, нечеткие гибридные операции), возникает проблема применимости существующих теоретических результатов к усовершенствованию методологической основы проектирования нечетких систем. В статье рассматривается схема нечеткого логического вывода, приводятся результаты экспериментального исследования и рекомендации по выбору функционального представления компонент. Научная значимость полученных результатов заключается в том, что представленные способы формирования механизма нечеткого логического вывода позволят улучшить аппроксимирующие свойства нечетких систем.

Ключевые слова: нечеткая система, нечеткий логический вывод, треугольные нормы и конормы.

ASPECTS OF THE IMPLEMENTATION OF THE FUZZY INFERENCE MECHANISM IN FUZZY SYSTEMS

Research article

Ledeneva T.M.¹, ReshetnikovA.D.^2, *

¹ ORCID: 0000-0002-3944-2266;

² ORCID: 0000-0002-8217-3815;

^{1, 2} Voronezh State University, Voronezh, Russia

* Corresponding author (reshetnikov.alex93[at]gmail.com)

Abstract

Fuzzy systems are used for modeling, data analysis, forecasting, decision-making, and management in various subject areas, including those related to technical applications. A fuzzy system is a universal approximator, and it is known that any complex system can be approximated by a fuzzy system with any given accuracy if the functional representation of the fuzzy logic connectives that participate in the model is selected in a suitable way.  At the moment, a number of standard approaches have been formed; however, against the background of the development of the sections of the theory of fuzzy sets and fuzzy logic, which are related to the functional representation of fuzzy operations (various families of triangular norms and conorms and the implications generated by them, aggregation functions, fuzzy hybrid operations), there arises the problem of the applicability of existing theoretical results to the improvement of the methodological basis for the design of fuzzy systems. The article examines the scheme of fuzzy logical inference, presents the results of an experimental study, and provides recommendations for choosing the functional representation of components. The scientific significance of the obtained results lies in the fact that the presented methods of creating a fuzzy inference mechanism will improve the approximating properties of fuzzy systems.

Keywords: fuzzy system, fuzzy inference, triangular norms and conorms.

Введение

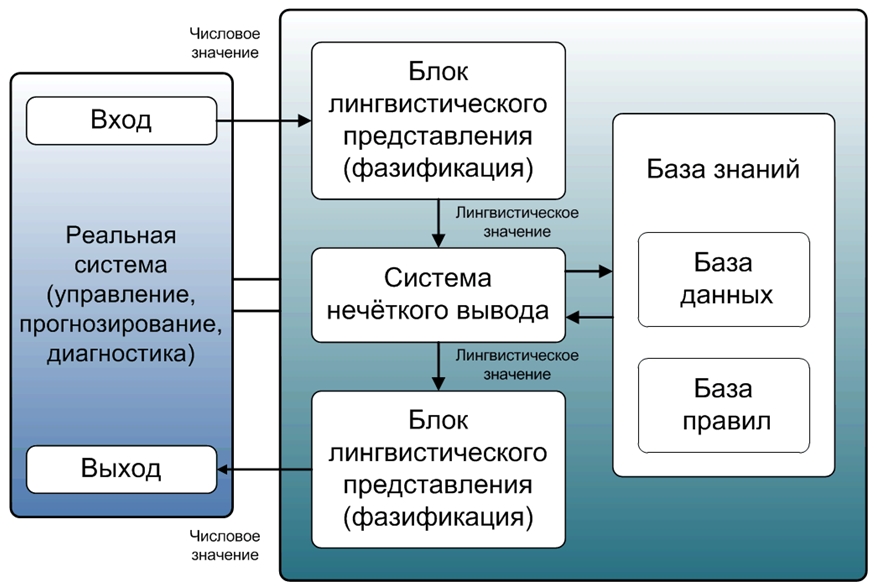
К настоящему времени нечеткие системы заняли устойчивую позицию среди информационных технологий, которые принято считать интеллектуальными. Ядром нечеткой системы является база знаний, причем для представления знаний используется продукционная модель, поэтому под нечеткими системами подразумеваются, прежде всего, нечеткие продукционные системы. Нечеткая продукционная система имеет структуру, представленную на рис. 1.

Рис. 1 – Структура нечеткой системы

 

Наиболее распространенные подходы к проектированию нечетких систем основаны на моделях Мамдани, Такаги-Сугено, Ларсена, Цукамото. Первые две модели реализованы в Fuzzy Logic Tool Box MATLAB, также нечеткие системы можно разрабатывать в FuzzyTech и FuzzyClips.

Проблема повышения качества аппроксимации для нечетких систем рассматривалась многими исследователями. Поскольку база знаний и, в частности, база правил являются ядром всякой нечеткой системы, отвечая за конкретное приложение, то обеспечение их качества является одним из направлений совершенствования нечетких систем [1], [2], [3]. Качество базы правил обеспечивается как на уровне формирования лингвистических шкал, так и относительно самой базы правил, ее наполнения и структуры. В [4] сформирован перечень требований к лингвистической шкале, которые повышают качество нечетких моделей: оптимальный уровень гранулированности, различимость термов, полнота, комплементарность и др. Широкое использование получают автоматизированные процедуры настройки лингвистических шкал на основе процедур кластеризации, в основе которых лежит задача минимизации отклонений тестовых данных от модельных значений, формируемых нечеткой системой. Для решения данной задачи используются генетические и другие эвристические алгоритмы [5]. В [6] предложены варианты правил, учитывающие форму кластеров. В [3], [7], [8] отмечается, что наибольшее влияние на качество аппроксимации, помимо качества базы правил, оказывает представление нечетких логических операций в системе логического вывода и выбор метода дефазификации.

Пусть x - входная переменная со значениями во множестве X, y - выходная переменная со значениями во множестве Y, причем для каждой из переменных также построены лингвистические шкалы, включающие множество термов  соответственно. Функционирование нечеткой системы осуществляется следующим образом:

1. На вход системы поступает числовое значение 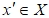 наблюдаемой переменной x, которое в блоке фазификации преобразуется в нечеткое множество, используемое в дальнейшем наряду с базой правил системой нечеткого логического вывода.
2. В системе логического вывода на основе композиционного правила вывода и базы правил формируется нечеткое множество, соответствующее выходной переменной y.

В блоке дефазификации осуществляется переход от выходного нечеткого множества к числовому значению, которое соответствует выходной переменной . Наиболее часто в приложениях используются следующие методы дефазификации: метод центра тяжести, метод центра площади, метод левого (правого) модального значения.

Цель статьи заключается в экспериментальном исследовании влияния функционального представления нечетких логических связок в механизме нечеткого логического вывода на уровень аппроксимирующих свойств нечетких систем.

В разделе 1 дается представление о механизме нечеткого логического вывода, функционирование которого определяется способом задания операций композиции и импликации, схем и функций агрегирования. Вариант реализации механизма логического вывода представлен кортежем. Раздел 2 посвящен функциональному представлению нечетких логических связок в механизме логического вывода. К основным операциям относятся треугольные нормы и конормы, которые моделируют связки и и или в нечетких моделях. Перечислены основные классы этих операций, а также новое семейство (10). На основе данных операций формируются импликация и операции композиции. В данном разделе рассматриваются все известные на данный момент классы импликаций. Известно, что выбор импликации оказывает существенное влияние на качество аппроксимации, и этот факт установлен в предыдущих исследованиях авторов [3], [7]. Формирование значения выходной переменной осуществляется с использованием функции агрегирования, соответствующей выбранной схеме агрегирования. Таким образом, в разделе 2 формируется информационная среда для построения множества алгоритмов (или механизмов) логического вывода. В разделе 3 осуществляется экспериментальное исследование различных алгоритмов вывода с целью исследования качества аппроксимации для тестовых баз правил. Качество аппроксимации оценивается среднеквадратической ошибкой отклонения. В данном разделе представлены некоторые результаты проведенного исследования.

1. Механизм нечеткого логического вывода

Основой механизма нечеткого логического вывода является схема правильных рассуждений modus ponens (рис. 2).

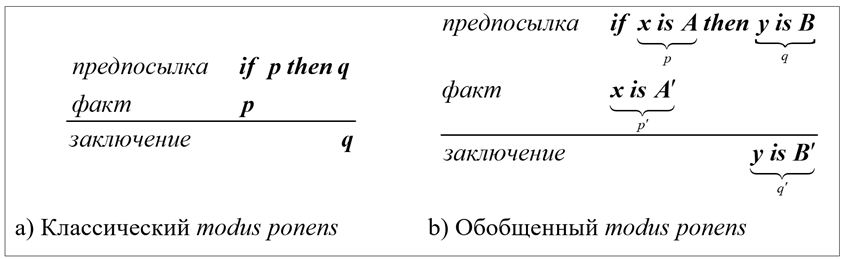
Рис. 2 – Схемы правильных рассуждений

 

Значение  выходной переменной y, соответствующее значению  входной переменной x, при наличии правила , определяется по формуле  (здесь символом ° обозначена операция композиции, → - импликация), которая может быть записана в виде

 

где ° соответствует -композиции;  T - треугольная норма; I - импликация, представляющая продукционное правило  - функции принадлежности соответствующих нечетких множеств.

Поскольку операция композиции и импликация могут быть определены неоднозначно и должны быть определенным образом специфицированы, то выбор конкретных представлений определяет некоторый алгоритм, который реализует нечеткий логический вывод.

Совокупность правил  образует базу правил , поэтому при формировании выходного нечеткого множества  важно определиться со схемами и операциями операции агрегирования. В [3] определены следующие основные схемы агрегирования:

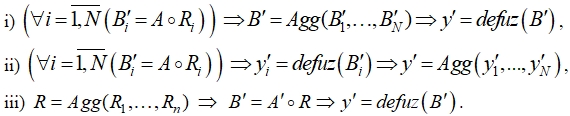
Заметим, что в случае i) вывод осуществляется раздельно, для каждого правила формируется выходное нечеткое множество, а затем осуществляется их агрегирование на основе операций, предназначенных для нечетких множеств. В случае ii), в отличие от предыдущего, каждое выходное нечеткое множество подвергается дефазификации, а затем осуществляется агрегирование полученных числовых значений. Случай iii) предполагает, что на основе бинарных отношений, соответствующих нечетким продукционным правилам, вначале строится обобщенное бинарное отношение, а затем на его основе формируется выходное нечеткое множество. Таким образом, выбор схемы агрегирования обусловливает использование тех функций и операций агрегирования, которые работают с определенным типом математических структур.

Вариант реализации механизма логического вывода (Fuzzy inference system) представим кортежем , где I - нечеткая импликация; T - треугольная норма;  - соответственно схема и операция агрегирования.

В рамках проведенного экспериментального исследования рассматриваются варианты  с различными представлениями компонент, которые, по сути, определяют некоторый алгоритм функционирования нечеткой системы.

       2. Функциональное представление нечетких логических связок 2.1 Треугольные нормы и конормы [9]

Треугольной нормой ( t-нормой) называется монотонная, коммутативная и ассоциативная бинарная операция , такая что для любого .

Треугольной конормой ( t-конормой) называется бинарная операция , такая, что для всех  выполняются свойства коммутативности, ассоциативности, монотонности, а также свойство .

Системы  являются абелевыми полугруппами с нейтральным элементом 0 и 1 соответственно и отношением порядка ≤. Характеристическим свойством треугольных норм и конорм является возможность их представления с помощью аддитивных (а также мультипликативных) генераторов [10], [11], [12].

Для непрерывной треугольной нормы T можно рассматривать остаточную треугольную норму , определяемую следующим образом [9]:

Операции T и S называются двойственными, если существует операция сильного отрицания , такая что .

Примеры двойственных треугольных норм и конорм, полученных разными исследователями, представлены в табл. 1. Классические операции  не удовлетворяют только законам комплементарности. Однако эти операции являются малочувствительными к исходной информации, что сказывается на качестве нечетких моделей. Для остальных пар нечетких операций, приведенных в таблице, не выполняются законы дистрибутивности и идемпотентности, что сокращает возможности равносильных преобразований. Формулы (10) являются обобщениями треугольных норм и конорм в классе рациональных функций при условии, что соответствующие аддитивные генераторы представлены дробно-линейной функцией [10]. Преимуществом операций (6)-(10) является наличие параметров. Их настройка на тестовых примерах позволяет обеспечить гибкость нечетких моделей и их адаптацию к конкретной задаче.

 

Таблица 1 – Основные классы треугольных норм и конорм

На рис. 3 представлены графики некоторых треугольных норм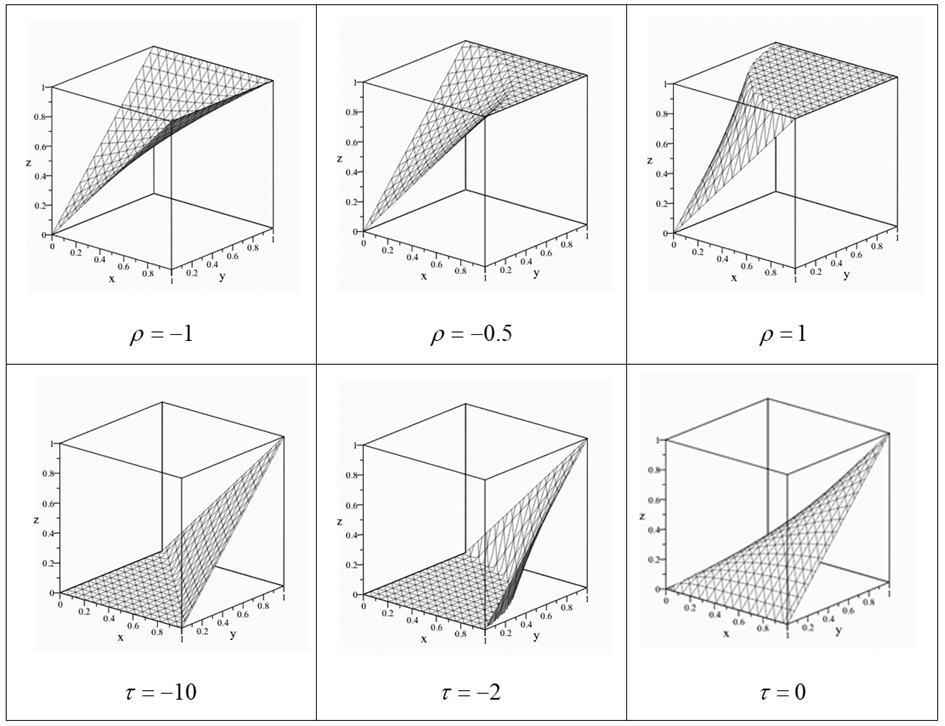  и конорм , позволяющие увидеть особенности их поверхностей.  

Рис. 3 – Графики треугольных норм и конорм (10)

 

В нечетких системах треугольная норма используется как функция агрегирования, формализующая связку и, а также для определения операции композиции. Пусть  - нечеткие бинарные отношения с функциями принадлежности . В общем виде операции композиции определяются с помощью треугольных норм и конорм следующим образом:

-композиции с функциями принадлежности

-композиция с функцией принадлежности

В известных алгоритмах логического вывода используется максминная композиция, что обусловлено наличием у нее некоторых замечательных свойств, среди которых отметим следующие: ассоциативность, дистрибутивность относительно max-объединения (но не дистрибутивна относительно min-пересечения); монотонность. Помимо максминной композиции, используется (но крайне редко) максмультипликативная композиция с функцией принадлежности

Для треугольных норм, также как и для конорм, можно построить ранжирование значений для фиксированных x и y. Это позволяет сравнивать выходные нечеткие множества, полученные с помощью различных композиций.

2.2 Нечеткая импликация

Нечеткая импликация играет важнейшую роль для формализации продукционных правил вида если x, то y (если-то-правил). Самый простой способ порождения нечеткой импликации – обобщение булевой импликации, при этом в точках (0,0), (0,1), (1,0), (1,1) должно выполняться определение четкой импликации. Однако возможно использование и других булевых функций.

В [13] определены следующие классы нечетких импликаций:

1) Импликации, представимые треугольными нормами, среди которых наиболее известными являются импликации Mamdami

2) Импликации, представимые остаточной треугольной нормой, примерами которых являются

импликация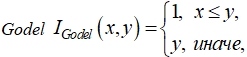

импликация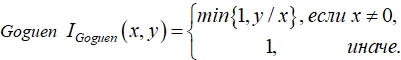

3) Импликации, полученные обобщением булевой импликации вида

 

где S - треугольная конорма. Для стандартного отрицания  данная формула  преобразуется в следующую

Используя классическую дизъюнкцию , получим импликацию Diene вида . Треугольная конорма  (табл. 1) позволяет получить импликацию Mizumoto . На основе треугольной конормы  получается импликация Lukasevich . Известно, что для пары двойственных операций  помимо стандартного отрицания «действует» параметрическое отрицание вида 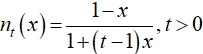. На основе конормы  и данного отрицания можно определить импликацию Sugeno

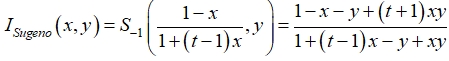
4) Импликации, полученные на основе нечеткой эквиваленции, имеют представление

где T  - треугольная норма, I  - импликация. Известными нечеткими эквиваленциями являются следующие:

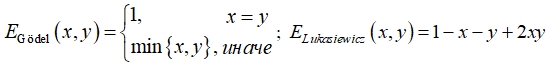
Используя определения треугольных норм и конорм из табл. 1 и соответствующих им операций отрицания, можно рассматривать и другие представления эквиваленций.

5) Импликации, полученные на основе функции расстояния, представляются в виде

где  – функция расстояния.

6) QM-импликации основаны на следующем представлении:

тогда переходя к нечетким операциям, получим

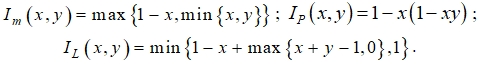  Для основных норм и соответствующих им конорм имеем QM-импликации следующего вида:   Известно, что выбор импликации оказывает наибольшее влияние на качество аппроксимации для нечетких систем. В [13] определены некоторые условия, которые обусловливают «хорошее поведение» импликаций.

2.3 Операции агрегирования

Под функцией агрегирования будем понимать преобразование, которое векторной оценке ставит в соответствие скалярную величину, при этом различают конъюнктивную, дизъюнктивную и компромиссную стратегии агрегирования. Дизъюнктивная стратегия моделируется T-нормами, конъюнктивная – S-конормами. Основу компромиссной стратегии составляют операции осреднения [14]. Перспективный класс для моделирования нечетких систем образуют порядковые операторы агрегирования (OWA-оператор - Ordered Weighted Averaging Operator), поскольку с помощью весовых коэффициентов, ассоциированных с данными операторами, можно моделировать стратегии агрегирования, отношение к риску и энтропию, а также формировать принципы согласования решений (например, при агрегировании учитывать не все правила, а большинство, почти все, как можно больше и т.д. – такой принцип согласования решений называется принципом нечеткого большинства) [15].

В зависимости от схемы агрегирования сформулируем несколько вариантов реализации механизма нечеткого логического вывода для системы с n входными переменными и одной выходной переменной.

Алгоритм 1 вывода, основанный на агрегировании правил

Шаг 1. Составить функцию принадлежности  нечеткого множества , которое соответствует значению  входной переменной X.

Шаг 2. Составить функцию принадлежности импликации , которая соответствует правилу .

Шаг 3. Составить функцию принадлежности нечеткого множества, описывающего комбинацию правил в виде 

Шаг 4. Для заданного нечеткого множества  с учетом выбранной операции композиции вычислить выходное нечеткое множество .

Алгоритм 2 вывода, основанный на агрегировании выходных нечетких множеств, соответствующих отдельным правилам

Шаги 1 и 2 реализуются так же, как в первом алгоритме.

Шаг 3. Для заданного нечеткого множества  с учетом выбранной операции композиции для каждого правила вычислить выходное нечеткое множество  с функцией принадлежности

 

Шаг 4. С учетом выбранной операции агрегирования вычислить выходное нечеткое множество B с функцией принадлежности

Алгоритм 3 вывода, основанный на агрегировании значений выходной переменной, соответствующих отдельным правилам

Шаги 1 и 2 реализуются так же, как в первом алгоритме.

Шаг 3 реализуется так же, как во втором алгоритме.

Шаг 4. К каждому нечеткому множеству  применить выбранный метод дефазификации и получить соответствующее значение .

Шаг 5. Вычислить  с использованием операций агрегирования из класса средних.

Заметим, что в каждом из алгоритмов используется свой класс операций агрегирования.

     3. Экспериментальные исследования различных реализаций механизма нечеткого логического вывода

Существующее многообразие представлений нечетких логических операций обусловливает необходимость их обоснованного выбора при проектировании нечетких систем. В наиболее известным методе логического вывода, который, например, имеется в MatLab выходное нечеткое множество определяется формулой (вывод Мамдани)

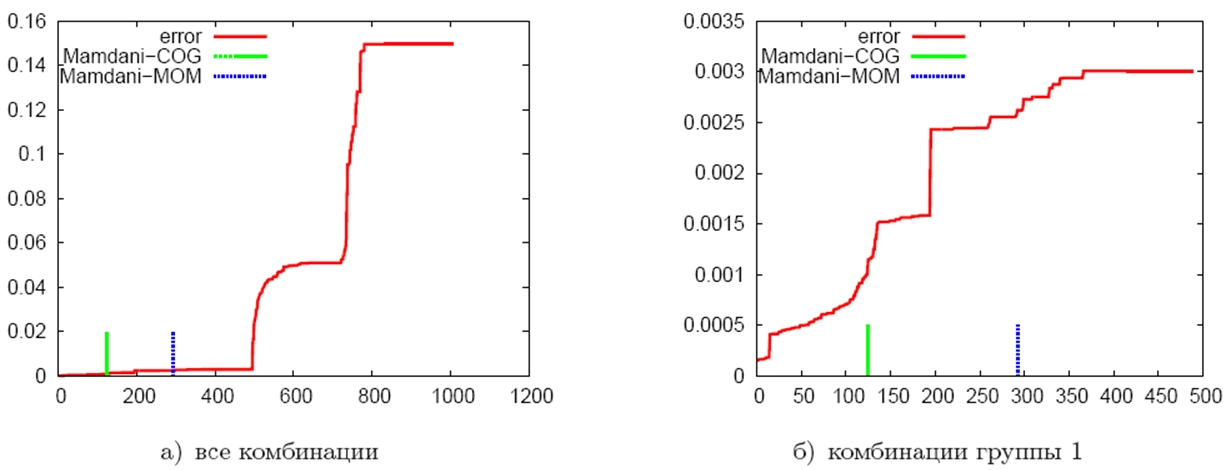
Однако эксперименты показывают, что формула может быть улучшена. На рис. 4 представлен график зависимости средней ошибки аппроксимации при различных реализациях системы нечеткого логического вывода на тестовых базах правил. Всего было сгенерировано 1024 методов логического вывода, в которых наряду с определением  также исследовались различные методы дефазификации. Зеленым и синим цветом отмечены позиции метода Мамдани, но с различными методами дефазификации. Видно, что за счет выбора подходящих компонент системы нечеткого логического вывода можно обеспечить высокий уровень качества аппроксимации, что подтверждает истинность теоремы об аппроксимации для нечетких систем [8].

Рис. 4 – Графики усредненной ошибки аппроксимации для сгенерированных методов нечеткого логического вывода (всего 1024 метода, используется набор тестовых баз правил)

 

Перечислим некоторые результаты экспериментов.

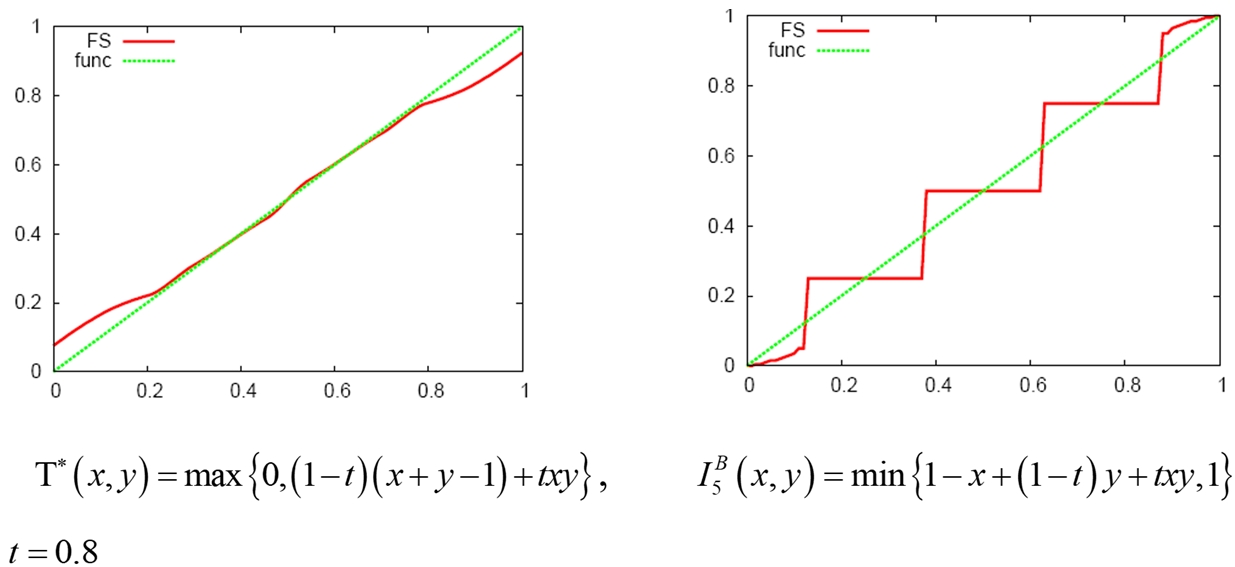
a. На рис. 5 представлены кривые, которые порождаются системами логического вывода с различными импликациями.

Рис. 5 - Графики аппроксимирующей кривой (красная линия) для различных импликаций при фиксированном выборе других компонент логического вывода

 

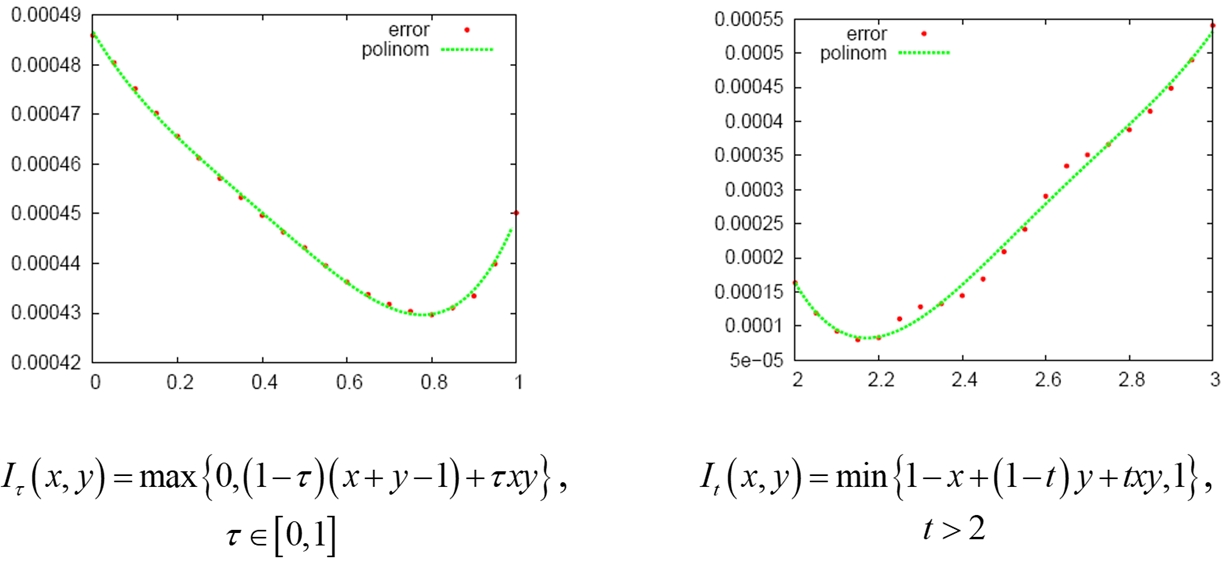
b. Целесообразно использовать параметрические операции импликации, которые за счет настройки параметра позволяют обеспечить хорошее качество аппроксимации. На рис. 6 представлен график зависимости ошибки от значений параметра параметрической импликации. Видно, что при определенных значениях параметра ошибка минимальна.

Рис. 6 - Зависимость ошибки аппроксимации от значений параметров импликаций

 

Проведенные экспериментальные исследования подтвердили, что импликации  действительно являются хорошими и совместно с методом дефазификации COG обеспечивают качественную аппроксимацию, но параметрические импликации могут показывать лучшие результаты и за счет настройки параметров гибко реагировать на особенности решаемой прикладной задачи.

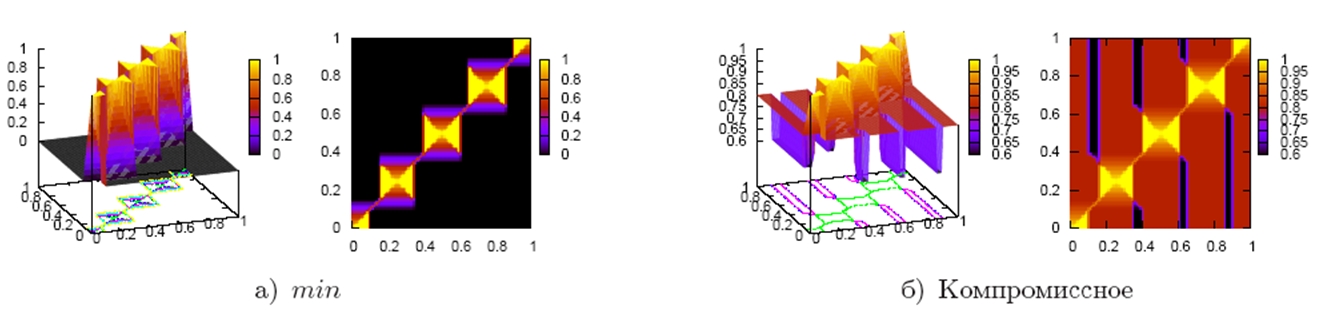
c.На качество аппроксимации также оказывает влияние операция агрегирования. В проведенном исследовании рассматривалась схема, в которой осуществлялось агрегирование правил. На рис. 7 представлена визуализация базы правил в случае, если их агрегирование осуществлялось с помощью операции и на основе аддитивной взвешенной свертки с весовыми коэффициентами, которые отражают значимость отдельных правил.

Рис. 7 – Графическое представление базы правил для различных случаев операции агрегирования

 

Таким образом, за счет подходящего выбора компонент механизма логического вывода можно получить более качественную реализацию нечеткой системы с точки зрения ее аппроксимирующих свойств.

    4. Практическая реализация

Результаты проведенного исследования использовались при разработке нечетких систем, среди которых экспертная система для принятия решений при проектировании системы вентиляции и кондиционирования воздуха; нечеткая система диагностики типа анемии на основе показателей крови; нечеткая система для прогнозирования прироста древесины при определении территории с лучшими почвенно-климатическими условиями для выращивания некоторых пород деревьев; нечеткая система для оценки кредитоспособности; нечеткая система управления целенаправленным движением мобильного объекта. Остановимся подробнее на описании экспертной системы, которая на основе измеренных датчиками или смоделированных значений показателей воздушной среды оценивает степень комфортности соответствующего помещения [16]. Основным параметром, оценивающим уровень комфорта/дискомфорта в помещении, является индекс комфортности PMV, который можно рассчитать в каждой точке объема. Данный индекс зависит от ряда параметров: DR – параметр, характеризующий наличие сквозняка в помещении, и зависящий, в том числе, от степени турбулентности воздуха; PD₁ – параметр, оценивающий дискомфорт, вызванный градиентом температуры по высоте помещения; PD₂ – параметр, оценивающий дискомфорт, вызванный значением температуры в зоне пола; PD₃ – параметр, который оценивает дискомфорт, вызванный асимметрией теплового излучения. В зависимости от значения перечисленных параметров в каждой точке объема можно определить категорию комфортности A, B или C, причем упорядочение этих категорий имеет вид , т.е. категория A  имеет самый высокий приоритет, а C – самый низкий. Категория D соответствует дискомфорту.

Используемая в настоящее время методика позволяет сделать вывод о категории комфортности на основе интервальных значений показателей. Однако при этом возникает проблема на границах интервалов, когда значение может быть отнесено и к данной, и к соседней категории. В разработанной экспертной системе проблема, связанная с применением противоречивых правил принятия решений, решается за счет использования инструментов нечеткого моделирования, с помощью которых уровень комфортности определяется однозначно. Если уровень комфортности определен в каждой точке, то система сформирует комплексную оценку комфортности помещения на основе современных подходов к агрегированию информации.

При работе с экспертной системой выполняется следующая последовательность действий:

1. Проект помещения разбивается на значимые и незначимые зоны; в каждой из зон определяется количество точек N, в которых осуществляется замер всех наблюдаемых параметров.
2. С помощью нечеткой системы формируется массив категорий комфортности в каждой из N точек.
3. Осуществляется формирование набора инструментов (фиксация параметров, выбор операции агрегирования, определение вектора весов и др.) для нахождения обобщенной оценки комфортности для каждой зоны.
4. Вычисляется обобщенная оценка для всего помещения в целом с учетом разработанных рекомендаций по выбору функций агрегирования.

Наиболее трудоемкий процесс создания данной экспертной системы был связан с разработкой нечеткой системы, при этом в основу механизма нечеткого логического вывода были положены результаты и выводы проведенных исследований, которые изложены выше. Для формирования базы правил использовалась существующая методика оценки комфортности, но при формировании лингвистических шкал параметров осуществлялся переход от заданного интервала к нечеткой переменной  с треугольной функцией принадлежности. Ее модальное значение в точности определяет интервал значений исходного параметра, соответствующий данной категории. В терминах новых переменных была разработана база правил. Примеры правил представлены ниже.

 

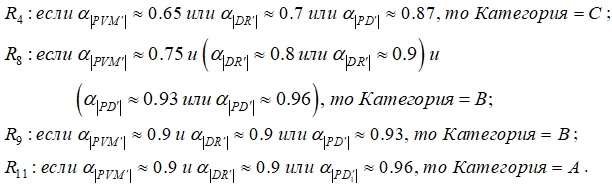
Используя нечеткую систему для каждой точки помещения можно определить соответствующую категорию. К особенностям подхода относятся: возможность учета требований к различным зонам в помещении; многоальтернативность и гибкость при формировании обобщенной оценки проекта.

Заключение

Нечеткие продукционные системы в отличие от обычных имеют ряд особенностей: формат правил может быть различным; для представления приближенных (неточных, нечетких) значений системных переменных используется лингвистический подход; алгоритмы формирования фронта готовых продукций упрощаются за счет использования для каждого правила оценок истинности. Однако в случае нечетких продукционных систем возникают другие проблемы, решение которых существенно влияет на эффективность и качество результата логического вывода. К таким проблемам, в частности, относится выбор представлений нечетких логических связок, методов дефазификации и фазификации, способов объединения результатов вывода, полученных для различных продукционных правил. Большинство этих вопросов решаются в представленной статье. Показано, что вариантов реализации нечеткого логического вывода может быть достаточно много, при этом целесообразно использовать параметрические формы, которые позволяют настраивать параметр на информационную среду конкретной прикладной задачи и обеспечить лучшее качество ее решения. 

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Dadone, P. Design Optimization of Fuzzy Logic Systems / P. Dadone. – Blacksburg, 2001. – 197 p.
2. Kandel A. Fuzzy Control Systems / A. Kandel, G. Landholz. – Boca Raton: CRC Press, 1994. – 656 p.
3. Ledeneva, T. Special Aspects of the Fuzzy Inference Mechanism / T. Ledeneva // Proceedings – 2020 2^nd International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency, SUMMA 2020. - - P. 128-132.
4. Pegat, A. Fuzzy modelling and control. / A. Pegat. – Moscow: BINOM, 2009. – 798 p.
5. Mishra, S. K. An empirical study of the performance of heuristic methods for clustering / S. K Mishra, V. V Raghavan // Pattern Recognition in Practice. – 1994. – P. 425–436.
6. Леденева, Т.М. Об одном подходе к формированию базы знаний для сегментации временных рядов / Т.М. Леденева, М.А. Сергиенко // Вестн. Воронеж. гос. ун-та. Серия: Системный анализ и информационные технологии. – 2017. - №3. – С. 156-164.
7. Татаркин, Д.С. Исследование моделей нечеткого логического вывода / Д.С. Татаркин, Т.М. Леденева // Вестн. Воронеж. гос. ун-та. Серия: Системный анализ и информационные технологии. – 2006. - №2. – С. 110-118.
8. Wang L.-X. Fuzzy systems are universal approximators / L.-X. Wang // IEEE 1992 Intern. Conf. Fuzzy Systems. – San Diego, 1992. – P. 1163-1170.
9. Klement E. Triangular norms. Position paper II: general constructions and parameterized families / E. Klement, R. Mesiar, E. Pap // Fuzzy Set and Systems. – 2004. – №145. – P. 411-438.
10. Ledeneva, T. Additive generators of fuzzy operations in the form of linear fractional functions / T. Ledeneva // Fuzzy Set and System. – 2020. – № 386. – P. 1-24. DOI: 1016/j.fss.2019.03.005.
11. Ledeneva, T. New Family of Triangular Norms for Decreasing Generators in the Form of a Logarithm of a Linear Fractional Function / T. Ledeneva // Fuzzy Sets and Systems. – 2020. DOI: 10.1016/j.fss.2020.11.020
12. Ledeneva, T. Analysis of additive generators of fuzzy operations represented by rational functions / T. Ledeneva // Journal of Physics: Conf. Series. – 2018. – №973. doi :10.1088/1742-6596/973/1/012037.
13. Леденева, T.M. О нечетких импликациях, полученных обобщением булевой функции / Т.М. Леденева, А.В. Грибовский // Вестн. Воронеж. гос. ун-та. Серия: Математика. – 2003. - №2. - 189-196.
14. Леденева, Т.М. Агрегирование информации в оценочных системах / Т.М. Леденева, С.Л. Подвальный // Вестн. Воронеж. гос. ун-та. Серия: Системный анализ и информационные технологии. – 2016. - №4. - 155-164.
15. Леденева, Т.М. Обработка нечеткой информации. / Т.М. Леденева. – Воронеж: Воронежский государственный университет, 2006. – 233 с.
16. Леденева, Т.М. Экспертная система для оценки проектов воздухораспределения / Т.М. Леденева, А.Д. Решетников // Сб. труд. Междунар. науч.-техн. конф. «Математические методы в технике и технологиях», – СПб.: Изд-во Политехн. ун-та, 2017. – С. 119-126.

Список литературы на английском языке / References in English

1. Dadone, P. Design Optimization of Fuzzy Logic Systems / P. Dadone. – Blacksburg, 2001. – 197 p.
2. Kandel A. Fuzzy Control Systems / A. Kandel, G. Landholz. – Boca Raton: CRC Press, 1994. – 656 p.
3. Ledeneva, T. Special Aspects of the Fuzzy Inference Mechanism / T. Ledeneva // Proceedings – 2020 2^nd International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency, SUMMA 2020. - - P. 128-132.
4. Pegat, A. Fuzzy modelling and control. / A. Pegat. – Moscow: BINOM, 2009. – 798 p.
5. Mishra, S. K. An empirical study of the performance of heuristic methods for clustering / S. K Mishra, V. V Raghavan // Pattern Recognition in Practice. – 1994. – P. 425–436.
6. Ledeneva, T.M. Ob odnom podhode k formirovaniju bazy znanij dlja segmentacii vremennyh rjadov [On one approach to building a knowledge base for time series segmentation] / M. Ledeneva, M.A. Sergienko // Vestn. Voronezh. gos. un-ta. Serija: Sistemnyj analiz i informacionnye tehnologii [Bulletin of Voronezh State University. System analysis and information technologies]. – 2017. –№3. – P. 156-164. [in Russian]
7. Tatarkin, D.S. Issledovanie modelej nechetkogo logicheskogo vyvoda [Investigating Fuzzy Inference Models] / D.S. Tatarkin, T.M. Ledeneva // Voronezh. gos. un-ta. Serija: Sistemnyj analiz i informacionnye tehnologii [Bulletin of Voronezh State University. System analysis and information technologies]. – 2006. – №2. – P.110-118. [in Russian]
8. Wang L.-X. Fuzzy systems are universal approximators / L.-X. Wang // IEEE 1992 Intern. Conf. Fuzzy Systems. – San Diego, 1992. – P. 1163-1170.
9. Klement E. Triangular norms. Position paper II: general constructions and parameterized families / E. Klement, R. Mesiar, E. Pap // Fuzzy Set and Systems. – 2004. – №145. – P. 411-438.
10. Ledeneva, T. Additive generators of fuzzy operations in the form of linear fractional functions / T. Ledeneva // Fuzzy Set and System. – 2020. – № 386. – P. 1-24. DOI: 1016/j.fss.2019.03.005.
11. Ledeneva, T. New Family of Triangular Norms for Decreasing Generators in the Form of a Logarithm of a Linear Fractional Function / T. Ledeneva // Fuzzy Sets and Systems. – 2020. DOI: 10.1016/j.fss.2020.11.020.
12. Ledeneva, T. Analysis of additive generators of fuzzy operations represented by rational functions / T. Ledeneva // Journal of Physics: Conf. Series. – 2018. – №973. doi :10.1088/1742-6596/973/1/012037.
13. Ledeneva, T.M. O nechetkih implikacijah, poluchennyh obobshheniem bulevoj funkcii [On fuzzy implications obtained by generalisation of a Boolean function] / T.M. Ledeneva, A.V. Gribovsky // Voronezh. gos. un-ta. Serija: Matematika [Bulletin of Voronezh State University. Mathematics]. – 2003. – №2. – P. 189-196. [in Russian]
14. Ledeneva, T.M. Agregirovanie informacii v ocenochnyh sistemah [Aggregation of information in evaluation systems] / T.M. Ledeneva, S.L. Podvalny // Voronezh. gos. un-ta. Serija: Sistemnyj analiz i informacionnye tehnologii [Bulletin of Voronezh State University. System analysis and information technologies]. – 2016. - №4. - P. 155-164. [in Russian]
15. Ledeneva T.M. Obrabotka nechetkoj informacii [Processing of fuzzy information] / T.M. Ledeneva. – Voronezh: Voronezh State University, 2006. 233 p. [in Russian]
16. Ledeneva T.M. Jekspertnaja sistema dlja ocenki proektov vozduhoraspredelenija [Expert system for evaluating air distribution projects] / T.M. Ledeneva, A.D. Reshetnikov // trud. Mezhdunar. nauch.-tehn. konf. «Matematicheskie metody v tehnike i tehnologijah» [Proceedings of the International Scientific and Technical Conference "Mathematical Methods in Engineering and Technology"], – SPb.: Publishing House of the Polytechnic University, 2017. – P. 119-126. [in Russian]