Submit manuscript Sign in / Sign up
Advanced search
Article sections

A COMBINED METHODOLOGY FOR SUBSTANTIATING THE UNCERTAINTIES OF THE CALCULATED RESULTS WHEN CONDUCTING RISK ANALYSIS AND PREDICTING EMERGENCY SITUATIONS

Research article
Aleksandrov A.E.
Azhder T.B.
Stepanova I.V.
Yashnikov D.A.
Livinskaya L.B.
DOI:
https://doi.org/10.23670/IRJ.2021.108.6.007
Issue: № 6 (108), 2021
Published:
2021/06/17
PDF

КОМБИНИРОВАННАЯ МЕТОДИКА ДЛЯ ОБОСНОВАНИЯ НЕОПРЕДЕЛЕННОСТЕЙ РАСЧЕТНЫХ РЕЗУЛЬТАТОВ ПРИ ПРОВЕДЕНИИ АНАЛИЗА РИСКОВ И ПРОГНОЗИРОВАНИИ АВАРИЙНЫХ СИТУАЦИЙ

Научная статья

Александров А.Е.1, Аждер Т.Б.2, *, Степанова И.В.3, Яшников Д.А.4, Ливинская Л.Б.5

1, 2, 3, 5 МИРЭА - Российский технологический университет, Москва, Россия;

4 Научно-технический центр по ядерной и радиационной безопасности, Москва, Россия

* Корреспондирующий автор (AzhderTB[at]yandex.ru)

Аннотация

При проведении анализа рисков и прогнозировании аварийных ситуаций к расчетным моделям предъявляются требования по обоснованию значений погрешностей и неопределенностей полученных результатов. Реализация этих требований рассматривается, как правило, применительно к диапазонам изменения исходных данных расчетной модели, которые должны быть согласованы с предполагаемой предметной областью исследования, а также со значениями неопределенности расчетной модели. В работе приводится комбинированная методика, позволяющая рассчитывать неопределенность выходной характеристики, обусловленной как детерминированными исходными параметрами, так и случайными, а также корректировать диапазоны изменения исходных параметров для уменьшения неопределенности выходной характеристики. Разработанная методика была использована для расчета неопределенности выходной характеристики применительно к вероятностному анализу хрупкого разрушения трубопроводов первого контура РУ типа ВВЭР при различных условиях эксплуатации и в аварийных режимах.

Ключевые слова: анализа рисков, прогнозирование, погрешность, неопределенность, детерминированные параметры, вероятностный анализ.

A COMBINED METHODOLOGY FOR SUBSTANTIATING THE UNCERTAINTIES OF THE CALCULATED RESULTS WHEN CONDUCTING RISK ANALYSIS AND PREDICTING EMERGENCY SITUATIONS

Research article

Aleksandrov A.E.1, Azhder T.B.2, *, Stepanova I.V.3, Yashnikov D.A.4, Livinskaya L.B.5

1, 2, 3, 5 MIREA - Russian Technological University, Moscow, Russia;

4 Scientific and Engineering Centre for Nuclear and Radiation Safety, Moscow, Russia

* Corresponding author (AzhderTB[at]yandex.ru)

Abstract

When conducting risk analysis and predicting emergency situations, the calculation models are required to justify the values of errors and uncertainties of the results obtained. As a rule, the implementation of these requirements is viewed in relation to the ranges of changes in the initial data of the computational model, which must be consistent with the intended subject area of the study, as well as with the uncertainty values of the computational model. The article presents a combined method that allows for calculating the uncertainty of the output characteristic due to both deterministic initial parameters and random ones, as well as adjusting the ranges of changes in the initial parameters to reduce the uncertainty of the output characteristic. The developed method was used to calculate the uncertainty of the output characteristic in relation to the probabilistic analysis of the brittle fracture of the RU primary pipelines of the VVER type reactor plant under various operating conditions and in emergency conditions.

Keywords: risk analysis, forecasting, error, uncertainty, deterministic parameters, probabilistic analysis.

Введение

При проведении анализа рисков и прогнозировании аварийных ситуаций к расчетным моделям помимо прочих предъявляются требования по обоснованию значений погрешностей и неопределенностей полученных результатов [1]. Эти требования необходимо обеспечить также при проведении аттестации программ для ЭВМ, используемых применительно к объектам ядерной энергетики [2]. Реализация этих требований рассматривается, как правило, применительно к диапазонам изменения исходных данных расчетной модели, которые должны быть согласованы с предполагаемой предметной областью исследования. Для выбранных диапазонов могут присутствовать особенности расчетной модели, приводящие к ее высокой чувствительности по отдельным исходным параметрам, и, как следствие, к большой неопределенности выходной характеристики. Особенно часто данная ситуация возникает, когда в качестве исходных данных при моделировании используются как детерминированные, так и случайные параметры [5], [7], [9]. В связи с этим, появляется дополнительная задача при проведении расчетов, связанная с анализом выбранных диапазонов исходных параметров и согласованием их со значениями неопределенностей расчетной модели.

Для решения этой задачи была рассмотрена следующая методика, используемая в обычной практике, основанная на линеаризации исходной расчетной модели, и применяемая к детерминированным процессам [3]. Заданная связь, в этом случае, между исходными параметрами и выходной характеристикой расчетной модели может быть представлена в виде следующей функциональной зависимости:

01-08-2021 13-02-16   (1)

где 01-08-2021 13-02-27 - выходная характеристика расчетной модели,

01-08-2021 13-02-35 - исходные параметры расчетной модели.

Внесение погрешностей в исходные параметры 01-08-2021 13-02-44 приводит к возникновению неопределенности выходной характеристики 01-08-2021 13-02-54, которая может быть рассчитана на основе выше упомянутого метода линеаризации функции 01-08-2021 13-03-03 [4]. В соответствии с этим методом математическое ожидание выходной характеристики составит:

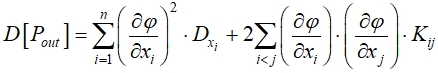01-08-2021 13-03-12   (2) а значение дисперсии: 01-08-2021 13-03-24    (3)

где 01-08-2021 13-03-34 - значение дисперсии для i-го исходного параметра,

01-08-2021 13-03-42 - коэффициент корреляции между i-ым и j-ым исходными параметрами.

Если исходные параметры некоррелированные (01-08-2021 13-03-42 =0), то формула (3) для вычисления дисперсии принимает более простой вид:

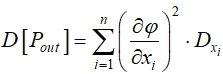01-08-2021 13-04-01    (4)

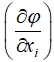где 01-08-2021 13-09-11- коэффициенты чувствительности i-го исходного параметра.

Задавая номинальные значения исходных параметров, и используя зависимости (1), (2) и (3), можно рассчитать неопределенность выходной характеристики, которая обусловлена используемой расчетной программой.

Комбинированная методика для обоснования неопределенностей расчетных результатов

Рассмотренная методика была модифицирована для случая, когда одна часть исходных данных является детерминированной, а другая часть – случайной, и использована применительно к вероятностному анализу хрупкого разрушения трубопроводов первого контура РУ типа ВВЭР при различных условиях эксплуатации и аварийных режимах. Для расчета неопределенности была использована объединенная модель, включающая вероятностную модель расчета хрупкого разрушения трубопроводов и моделирование случайных ошибок или неопределенностей методом Монте-Карло [9], [10]. В качестве исходных данных были использованы виртуальные данные, включающие истинные значения исходных параметров и их неопределенности, что дало возможность проследить влияние исходных параметров на результирующую неопределенность выходной характеристики. Аналогичный подход был использован в работе [5].

Принятые первоначальные значения исходных параметров и диапазоны их изменения, выбранные на основе экспертных оценок, составили:

1) вязкость разрушения – от 20 до 300 МПа√м;

2) напряжения, приведенные к постоянным – от 0 до 500 МПа;

3) математическое ожидание глубин трещин – от 0 до 0.017 м;

4) математическое ожидание длин трещин – от 0 до 0.051 м;

5) среднее квадратичное отклонение (СКО) глубин и длин трещин принималось равным 10 %; 20 %; 60 % от величины мат ожидания соответственно для глубин и длин.

При расчете вероятности разрушения трубопровода глубины и длины трещин рассматривались как случайные величины, имеющие заданные исходные распределения. При моделировании исходного распределения глубин и длин трещин использовался нормальный закон распределения. Моделирование распределения размеров трещин проводилось в диапазоне от 0 до 0,7 толщины стенки трубопровода. Толщина стенки принималась постоянной и равной s=0,065 м. Число экспериментов при выбранных значениях математического ожидания глубин и длин трещин принималось равным 01-08-2021 13-10-26 . Предварительные эксперименты с исходной расчетной моделью показали, что указанное число экспериментов обеспечивает устойчивые статистические значения для выходной характеристики. Остальные исходные параметры принимались детерминированными, изменяемыми в указанных выше диапазонах при исходных неопределенностях равных 10 % от выбранного номинального значения. Указанные неопределенности 10 % рассматривались как исходные данные и могли изменяться в зависимости от целей и задач проводимого эксперимента.

Выбор номинальных исходных параметров для каждого численного эксперимента проводился случайным образом из приведенного диапазона на основе равномерного распределения. Число экспериментов при формировании случайной выборки исходных параметров принималось равным 01-08-2021 13-10-38.

Сформированная таким образом совокупность исходных номинальных параметров использовалась для расчета выходной характеристики – вероятности хрупкого разрушения 01-08-2021 13-10-45 и ее неопределенности 01-08-2021 13-10-51.

Поскольку для рассматриваемой модели выходная характеристика определялась на основе разработанного алгоритма, то вычислить коэффициенты чувствительности 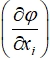01-08-2021 13-11-01, приведенные в формуле (4) аналитически невозможно. Поэтому коэффициенты чувствительности для каждого исходного параметра вычислялись с использованием конечно-разностных соотношений, на основе расчетного программного кода по следующей зависимости:

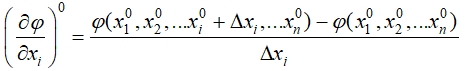01-08-2021 13-14-12  (5) где значения 01-08-2021 13-14-24 - вычислялись в точках номинальных значений исходных параметров.

Учитывая, что величина 01-08-2021 13-03-03 является случайной, то в формуле (5) для величины 01-08-2021 13-03-03 использовалось значение математического ожидания выходной характеристики, т.е.

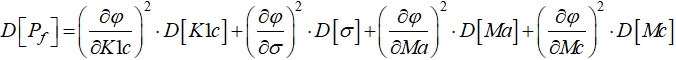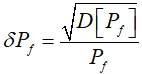01-08-2021 13-14-36    (6) Величина дисперсии выходной характеристики с учетом зависимости (4) может быть записана в виде следующей формулы: 01-08-2021 13-14-53     (7) где 01-08-2021 13-15-07 - заданные дисперсии для исходных параметров. Относительная неопределенность выходной характеристики составит: 01-08-2021 13-15-17   (8)

Для наглядного сопоставления влияния каждого из исходных параметров наряду с коэффициентами чувствительности, определяемыми по формуле (5), были вычислены также относительные неопределенности по каждому исходному параметру, рассчитываемые по следующим зависимостям:

С учетом (9-12) формула (8) может быть записана в виде:

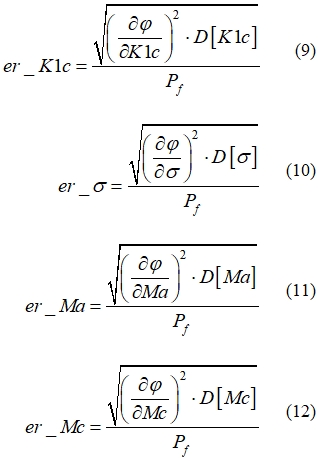01-08-2021 13-15-48 С учетом (9-12) формула (8) может быть записана в виде: 01-08-2021 13-20-38  

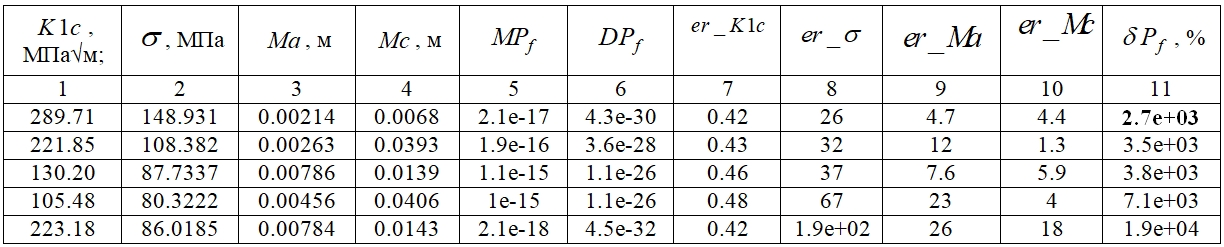
В результате проведенных численных экспериментов были получены неопределенности для всего массива значений исходных параметров во всем диапазоне их изменений. В таблице №1 приведены значения исходных параметров, а также рассчитанных выходных характеристик и относительных неопределенностей по каждому исходному параметру, для пяти наиболее высоких значений неопределенностей, полученных по результатам проведенного численного эксперимента. В заголовке столбцов таблицы использованы следующие сокращенные обозначения параметров:

1) исходные номинальные значения параметров: 01-08-2021 13-21-29 – вязкость разрушения; σ – напряжения, приведенные к постоянным значениям; Ma, Mc – математические ожидания глубин и длин трещин;

2) рассчитанные выходные характеристики: 01-08-2021 13-22-11– математическое ожидание вероятности хрупкого разрушения; 01-08-2021 13-23-36 – дисперсия вероятности разрушения; 01-08-2021 13-23-46 – относительные неопределенности по каждому исходному параметру; 01-08-2021 13-24-10,% – относительная неопределенность выходной характеристики в процентах.

 

Таблица 1 – Расчетные значения параметров, полученные для числа испытаний

01-08-2021 13-27-15

Примечание: n=1000 и СКО=60%  

Следует заметить, что полученные неопределенности (Таблица №1) имеют очень большие значения (значение относительной неопределенности выходной характеристики достигает величины 01-08-2021 13-24-10=19000 %).

Модификация исходной методики в части стратификации расчетных результатов по значению выходной характеристики

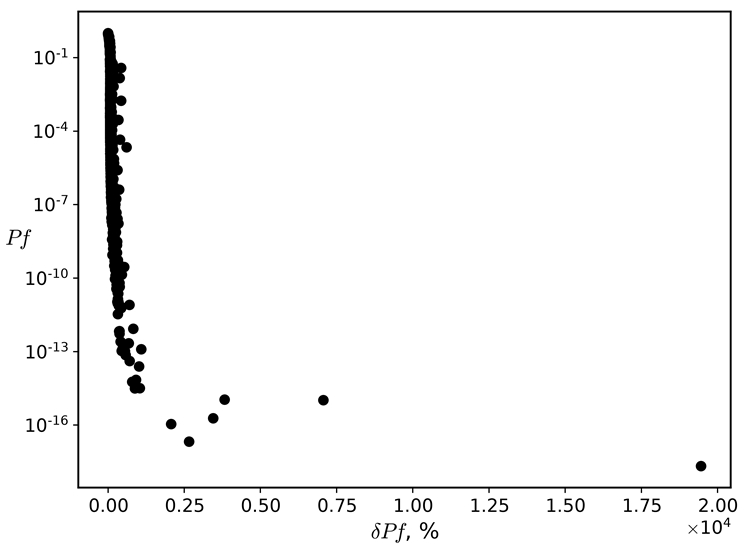
При анализе рассчитанных значений была обнаружена особенность в распределении неопределенности выходной характеристики, выраженная в том, что высокие значения неопределенности наблюдаются для очень малых значений вероятности разрушения. Отмеченная особенность приводит к мысли – представить полученные результаты в виде функциональной зависимости вероятности разрушения от значений полученных неопределенностей, которая приводится на рисунке 1. Характер приведенного распределения показывает, что значения неопределенностей могут быть стратифицированы по группам, выделенным по значению выходной характеристики. Такая стратифицированная выборка сохраняет консервативность значений неопределенностей, но разделяет их в зависимости от значений вероятности разрушения, что позволяет для высоких значений вероятности получить более реалистичные и существенно меньшие значения неопределенностей, сохранив, в то же время, их консервативность.

01-08-2021 13-31-16

Рис. 1 – Зависимость вероятности разрушения от ее неопределенности для всего диапазона изменений исходных параметров

 

На основе полученных результатов, приведенных на рисунке 1, в соответствии с предложенным способом, были выделены группы данных, сформированные по следующим признакам: 1-ая группа -10-01 ≤ Pf ≤ 1; 2-ая группа - 10-03 ≤ Pf  ≤ 10-01 ; 3-ая группа -10-07 ≤ Pf ≤ 1003; 4-ая группа -10-10 ≤ Pf  ≤ 10-07; 5-ая группа -10-16 ≤ Pf  ≤ 10-10.

Для каждой выделенной группы были определены максимальные значения неопределенности, которые составили:

1-ая группа - 10-01 ≤ Pf  ≤ 1;  = 88%.

2-ая группа -10-03 ≤ Pf  ≤ 10-01;  = 430%

3-ая группа - 10-07 ≤ Pf  ≤ 10-03;  = 610%;

4-ая группа -10-10 ≤ Pf  ≤ 10-07;  = 530%;

5-ая группа - 10-16 ≤ Pf  ≤ 10-10;  = 19000%.

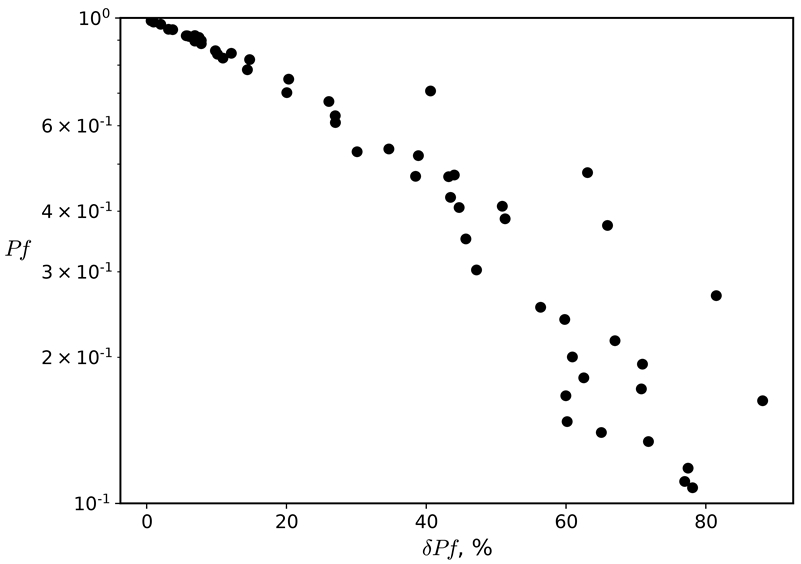
Результаты распределений значений вероятности разрушения от неопределенности для 1-ой группы приведены на рисунке 2. Для остальных групп характер изменения неопределенностей сохраняется, но с уменьшением вероятности разрушения увеличивается рассеянность значений неопределенности.

01-08-2021 13-31-37

Рис. 2 – Зависимость вероятности разрушения от ее неопределенности для 1 группы

Примечание: диапазон изменения вероятности 10-01 ≤ Pf  ≤ 1

 

Параметрический анализ относительных неопределенностей расчетной модели

Полученный в результате расчета набор данных, приведенных в таблице №1, позволяет провести дополнительный параметрический анализ о влиянии относительных неопределенностей по каждому исходному параметру, вносимых в результирующую неопределенность выходной характеристики. При этом было установлено, что основной вклад вносится двумя исходными параметрами: напряжением и вязкостью разрушения. Построив зависимости относительных неопределенностей для напряжения (01-08-2021 13-33-54 ) и вязкости разрушения (01-08-2021 13-34-01 ) от исходных параметров, можно определить области экстремальных значений для относительных неопределенностей, а по ним и области допустимых значений исходных параметров. Сужая области изменения исходных параметров, можно существенно уменьшить неопределенность выходной характеристики, управляя тем самым ее значением.

В соответствии с предложенной методикой были построены графики относительных неопределенностей для напряжения (01-08-2021 13-33-54) и вязкости разрушения (01-08-2021 13-34-01) в зависимости от исходных параметров. На рисунках 3 - 5 приведены выборочные графики относительных неопределенностей от исходных параметров, использованных в дальнейшем для параметрического анализа. Отметим следующие особенности поведения относительной неопределенности по напряжению 01-08-2021 13-33-54:

1) значительные величины неопределенностей находятся при самых низких выбранных значениях напряжения. Причем с уменьшением размеров трещин значения максимальных неопределенностей сильно возрастают.

2) области больших значений неопределенностей совпадают с областью малых значений вероятности хрупкого разрушения, что подтверждает полученные выше выводы.

Выделим также следующие особенности поведения относительной неопределенности по вязкости разрушения 01-08-2021 13-34-01:

1) максимальные значения неопределенностей наблюдаются при самых низких значениях исходных параметров вязкости разрушения и напряжения в заданных диапазонах изменения;

2) области больших значений неопределенностей так же, как и для неопределенностей по напряжению совпадают с областью малых значений вероятности хрупкого разрушения.

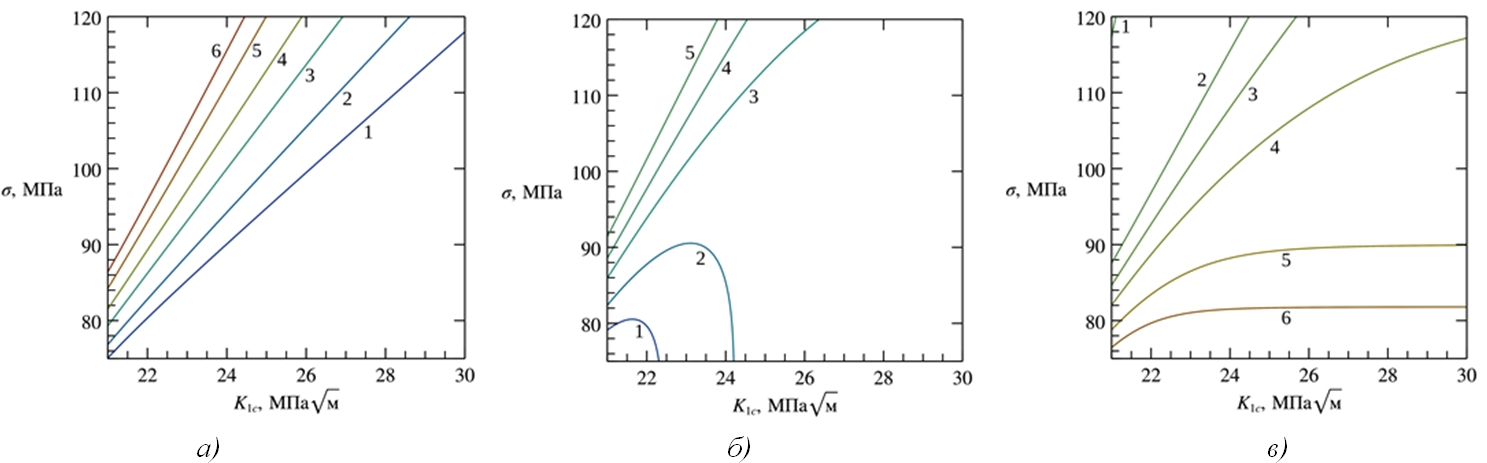
01-08-2021 13-40-22

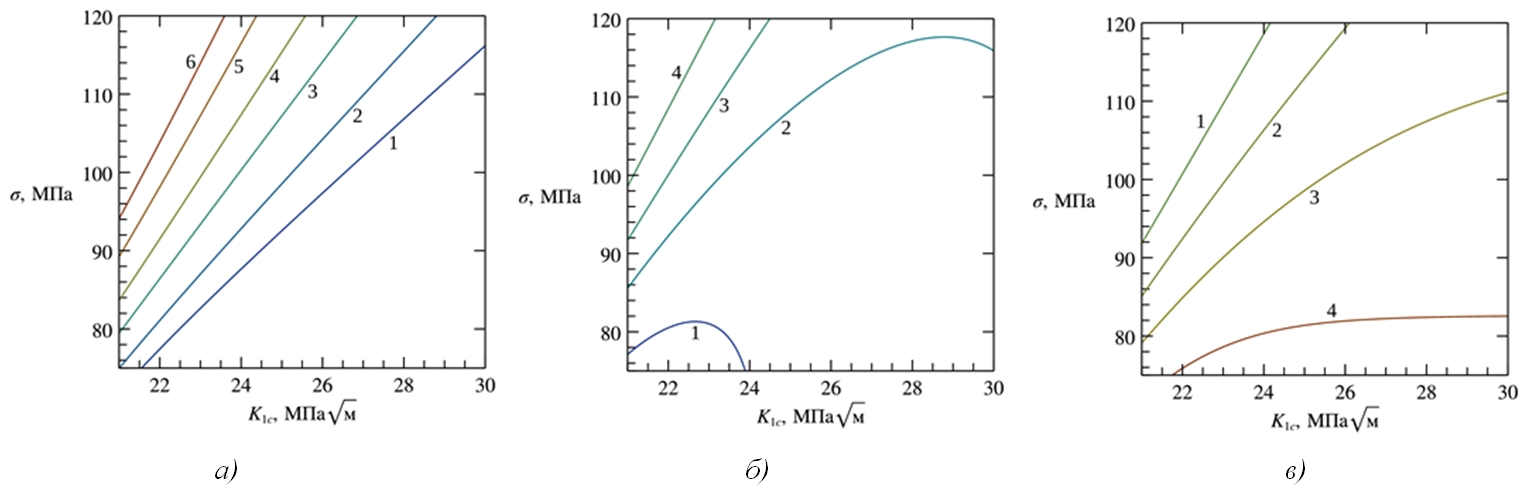
Рис. 3 – Зависимость вероятности разрушения и относительных неопределенностей от исходных параметров для значений: Ma=0,025; Mс=0,050; СКО=10%:

a) вероятность разрушения Pf;1 – 0,1; 2 – 0,2; 3 – 0,4; 4 – 0,6; 5 – 0,8; 6 – 0,9; б) относительная неопределенность 01-08-2021 13-37-41; 1 – 3; 2 – 2; 3 – 1; 4 – 0,5; 5 – 0,2; в) относительная неопределенность 01-08-2021 13-33-54; 1 – 0; 2 – 0,2; 3 – 0,5; 4–1; 5–2; 6–3

 

01-08-2021 13-40-36

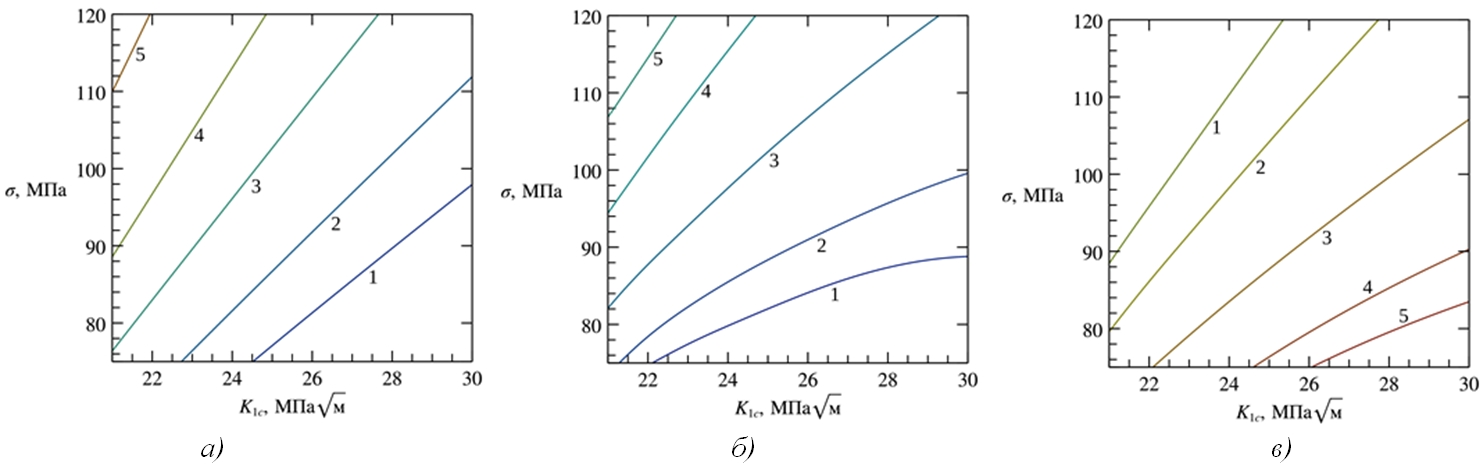
Рис. 4 – Зависимость вероятности разрушения и относительных неопределенностей от исходных параметров для Ma=0,025; Mс=0,050; СКО=20%:

a) вероятность разрушения Pf;1 – 0,1; 2 – 0,2; 3 – 0,4; 4 – 0,6; 5 – 0,8; 6 – 0,9; б) относительная неопределенность 01-08-2021 13-37-41 ; 1 – 2; 2 – 1; 3 – 0,5; 4 – 0,2; в) относительная неопределенность 01-08-2021 13-33-54; 1 – 0; 2 – 0,5; 3 – 1; 4 – 2

 

01-08-2021 13-40-53

Рис. 5 – Зависимость вероятности разрушения и относительных неопределенностей от исходных параметров для Ma=0,025; Mс=0,050; СКО=60%:

a) вероятность разрушения Pf;;1 – 0,1; 2 – 0,2; 3 – 0,4; 4 – 0,6; 5 – 0,8; б) относительная неопределенность 01-08-2021 13-37-41 ; 1 – 0,8; 2 – 0.7; 3–0,5; 4–0,3; 5–0,2; в) относительная неопределенность 01-08-2021 13-33-54; 1 – 0,2; 2 – 0,3; 3 – 0,5; 4–0,7; 5–0,8

 

На основе полученных результатов анализа принятые ранее значения исходных параметров были откорректированы, и выбраны новые:

1) вязкость разрушения – от 20 до 300 МПа√м;

2) напряжения, приведенные к постоянным – от 100 до 500 МПа;

3) математическое ожидание глубин трещин – от 10 до 17 мм;

4) математическое ожидание длин трещин – от 20 до 34 мм;

5) среднее квадратичное отклонение (СКО) глубин и длин трещин принималось равным10 %; 20 %; 60 % от величины мат ожидания соответственно для глубин и длин.

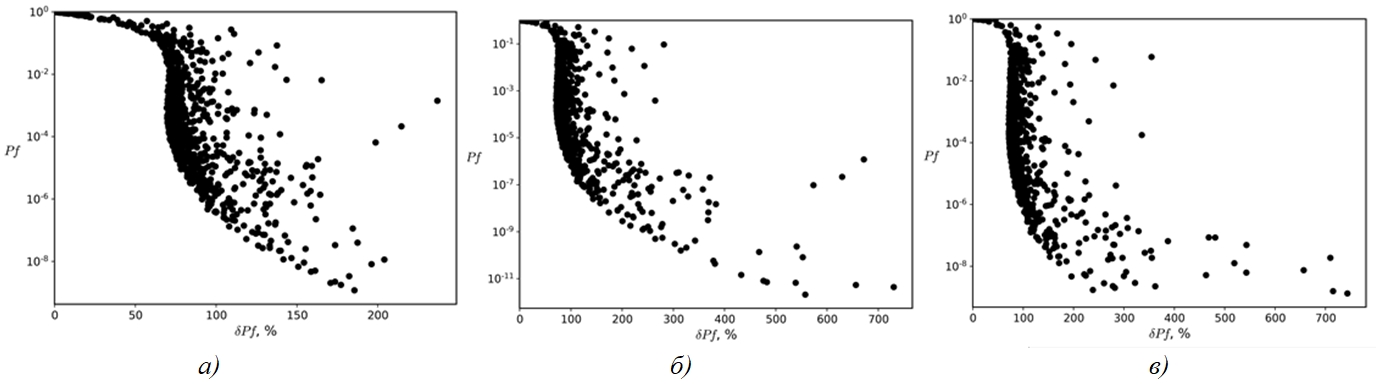
Выборочные результаты расчетов для новых диапазонов исходных данных приведены на рисунке 6. Анализ полученных данных для новых диапазонов показал, что максимальное значение неопределенности не превысило 740%, что явилось допустимым для проводимых расчетов. В случае получения значений неопределенностей, не удовлетворяющих исходным требованиям, необходимо выполнить новую итерацию по корректированию области исходных параметров.

01-08-2021 13-45-13

Рис. 6 – Зависимость вероятности разрушения от ее неопределенности для нового диапазона изменения исходных параметров:

а – СКО=60%; б – СКО=20%; в – СКО=10%

  Заключение

Предложена комбинированная методика, позволяющая рассчитывать неопределенность выходной характеристики для случая, когда одна часть исходных данных является детерминированной, а другая часть – случайной, а также корректировать диапазоны исходных параметров с целью обеспечения требуемой неопределенности выходной характеристики.

Разработанная методика была использована для расчета неопределенности выходной характеристики применительно к вероятностному анализу хрупкого разрушения трубопроводов первого контура РУ типа ВВЭР при различных условиях эксплуатации и в аварийных режимах. Для заданных диапазонов изменения исходных параметров, используемой расчетной модели, были проведены численные эксперименты и получены неопределенности выходной характеристики для всего объема значений исходных параметров.

Предложен способ формирования расчетных данных – разбиение их на группы в зависимости от значения выходной характеристики, что позволило исключить большие выбросы значений неопределенности для диапазонов выходной характеристики, используемых в практике расчетов.

Из анализа полученных экспериментальных данных были выделены наиболее значимые исходные параметры, вносящие наибольший вклад в значение неопределенности выходной характеристики. На основе полученных зависимостей относительных неопределенностей были откорректированы диапазоны изменения исходных параметров, что позволило получить реалистичные значения неопределенности выходной характеристики.

Конфликт интересов Не указан. Conflict of Interest None declared.

Список литературы / References

  1. Звонарев С. В. Основы математического моделирования: учебное пособие / С. В. Звонарев. – Екатеринбург: Изд‑во Урал. ун‑та, 2019. – 112 с.
  2. Порядок проведения экспертизы программ для электронных вычислительных машин, используемых в целях построения расчетных моделей процессов, влияющих на безопасность объектов использования атомной энергии и (или) видов деятельности в области использования атомной энергии. Утвержден приказом №325 ФСЭТАН от 30.07.2018г.
  3. Вентцель Е.С. Теория вероятностей / Е.С. Вентцель. – М.: Издательский центр «Академия», 2005. – 576 с.
  4. Вольперт А.И. Анализ в классах разрывных функций и уравнения математической физики / А.И.Вольперт, С.И.Худяев. – М.: Наука, 1975. – 395с.
  5. Ciroth, A. Uncertainty calculation in life cycle assessments / A. Ciroth, G. Fleischer, J. Steinbach. – Int J LCA 9, 2004. – 216 p.
  6. Самарский А. А. Математическое моделирование / А. А. Самарский, А.П. Михайлов. – М.: Наука. Физматлит, 1997. – 320 с.
  7. Строгалев В. П. Имитационное моделирование: учеб. пособие для вузов/ В. П. Строгалев, И. О. Толкачева. – М.: Изд‑во МГТУ им. Н. Э. Баумана, 2008.– 276 с.
  8. Пономарев В. Б. Математическое моделирование технологических процессов: курс лекций / В. Б. Пономарев, А. Б. Лошкарев. – Екатеринбург: ГОУ ВПО УГТУ‑УПИ, 2006. – 129 с.
  9. Ермаков С. М. Методы Монте–Карло и смежные вопросы / С.М.Ермаков. – М.: Наука, 1971.
  10. Попов Ю. П. Вычислительный эксперимент / Ю. П. Попов, А.А.Самарский. – М.: Знание, 1983. – 64 с.

Список литературы на английском языке / References in English

  1. Zvonarev S. V. Osnovy matematicheskogo modelirovanija: uchebnoe posobie [Fundamentals of Mathematical Modeling: A Textbook] / S. V. Zvonarev. - Yekaterinburg:‑Ural University Publishing House. ‑, 2019 – 112 p. [in Russian]
  2. Porjadok provedenija ehkspertizy programm dlja ehlektronnykh vychislitel'nykh mashin, ispol'zuemykh v celjakh postroenija raschetnykh modelejj processov, vlijajushhikh na bezopasnost' ob"ektov ispol'zovanija atomnojj ehnergii i (ili) vidov dejatel'nosti v oblasti ispol'zovanija atomnojj ehnergii. Utverzhden prikazom №325 FSEhTAN ot 30.07.2018g. [The procedure for the examination of programs for electronic computers used for the construction of computational models of processes that affect the safety of nuclear energy facilities and (or) activities in the field of nuclear energy use. Approved by Order No. 325 of The Federal Service for Environmental, Technological and Nuclear Supervision dated 30.07.2018] [in Russian]
  3. Wentzel E. S. Teorija verojatnostejj [Probability Theory] / E. S. Wentzel. - M.: Publishing house «Akademija», 2005. - 576 p. [in Russian]
  4. Volpert A. I. Analiz v klassakh razryvnykh funkcijj i uravnenija matematicheskojj fiziki [Analysis in classes of discontinuous functions and equations of mathematical physics] / A. I. Volpert, S. I. Khudyaev. - M.: Nauka, 1975 – 395 p.[in Russian]
  5. Ciroth, A. Uncertainty calculation in life cycle assessments / A. Ciroth, G. Fleischer, J. Steinbach. – Int J LCA 9, 2004. – 216 p.
  6. Samarsky A. A. Matematicheskoe modelirovanie [Mathematical modeling] / A. A. Samarsky, A. P. Mikhailov. - M.: Nauka. Fizmatlit, 1997. - 320 p. [in Russian]
  7. Strogalev V. P. Imitatsionnoe modelirovanie: ucheb. posobie dlya vuzov [Simulation Modeling: a Textbook] / V. P. Strogalev, I. O. Tolkacheva. - M.: Publishing House of the Bauman Moscow State Technical University.‑ , 2008 – - 276 p.[in Russian]
  8. Ponomarev V. B. Matematicheskoe modelirovanie tekhnologicheskikh processov: kurs lekcijj [Mathematical modeling of technological processes: course of lectures] / V. B. Ponomarev, A. B. Loshkarev. – Y‑ekaterinburg: Ural State Technical University, 2006. - 129 p. [in Russian]
  9. Ermakov S. M. Metody Monte–Karlo i smezhnye voprosy [Monte Carlo methods and related issues] / S. M. Ermakov. - Moscow: Nauka, 1971. [in Russian]
  10. Popov Yu. P. Vychislitel'nyjj ehksperiment [Computational experiment] / Yu. P. Popov, A. A. Samarsky. - Moscow: Znanie, 1983. – 64 p. [in Russian]