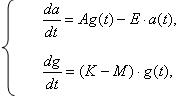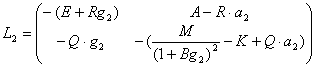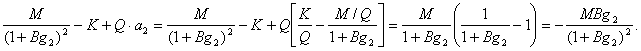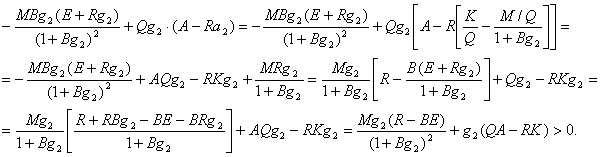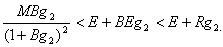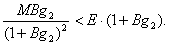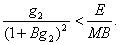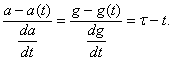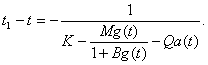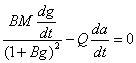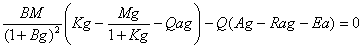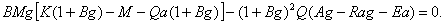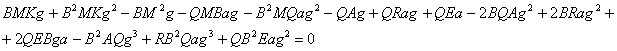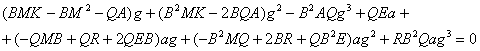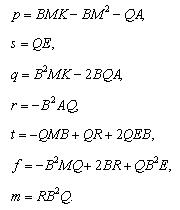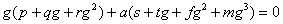УПРАВЛЕНИЕ ДИНАМИЧЕСКИМИ СИСТЕМАМИ МЕТОДОМ МИНИМИЗАЦИИ ПОДКАСАТЕЛЬНОЙ

Research article

Агранович Ю.Я.

Демёхина А.С.

Issue: № 5 (5), 2012

Published:

2012/10/31

PDF

УПРАВЛЕНИЕ ДИНАМИЧЕСКИМИ СИСТЕМАМИ МЕТОДОМ МИНИМИЗАЦИИ ПОДКАСАТЕЛЬНОЙ

Научная статья

Агранович Ю.Я.¹, Демёхина А.С.²

^{1, 2}Воронежский государственный технический университет, Воронеж, Россия

Аннотация

В данной работе предложен один из вариантов оптимального решения динамической задачи связанной с иммунным ответом организма при хроническом гепатите B. Решение основано на минимизации величины проекции подкасательной к точкам траектории системы на ось времени.

Ключевые слова: устойчивость динамических систем, минимум подкасательной.

Key words: stability of dynamical systems, a minimum subtangent.

В данной работе в качестве математического описания иммунного ответа организма на вирусную инфекцию использовалась модель Диброва-Лившица-Волькенштейна, которая представлена системой из двух дифференциальных уравнений с одним временем запаздывания:

(1)

где a(t) - количество специфических антител в 1 мл блоков иммунной системы (клетка/мл);

g(t) - количество вирусных частиц (HBV) в 1 мл блоков иммунной системы (клетка/мл);

T - время деления и дифференцировки стимулированных лимфоцитов (2:3 суток). Эта система зависит от семи переменных параметров и позволяет качественно описывать основные закономерности иммунного ответа организма. В связи с этим обстоятельством данная модель является наиболее подходящей для приложений в области лечения хронической формы гепатита В. Заметим, что хроническая форма заболевания предполагает значительно большее время, на порядок превосходящее время запаздывания Т, поэтому мы будем рассматривать систему (1), пренебрегая Т:

(2)

с некоторыми начальными данными a(0) = a₀, g(0) = g₀, которые соответствуют данным биохимического исследования в начале очередного обследования пациента.

Последующий анализ системы (2) направлен на решение следующих двух задач:

а) определение области устойчивости/неустойчивости стационарных решений системы соответствующих хронической форме заболевания и потому уничтожению вируса HBV;

б) определение оптимального времени вакцинации совместной с адъювантами, позволяющей в кратчайшие сроки вылечить хронического больного.

Стационарные точки системы

Для определения стационарных точек системы (2) решим следующую систему алгебраических уравнений:

(3)

Из второго уравнения получим

При g₁= 0 имеем a₁= 0. Эта стационарная точка соответствует полному выздоровлению. Подставляя a из (4) в первое уравнение (3) получим соотношение для определения g:

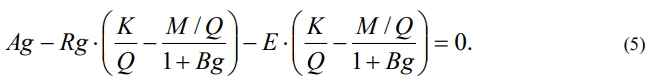
Откуда

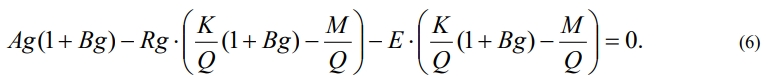
Из (6) после некоторых преобразований получим уравнение для определения g:

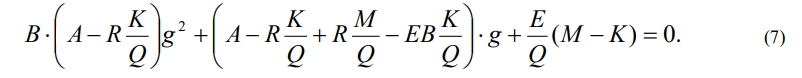
Дискриминант уравнения (7) равен

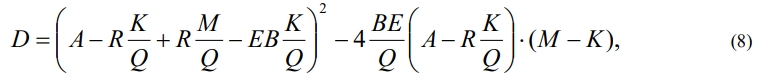
понятно, что, если D<0, то других стационарных точек, кроме (0,0) нет, т.е. хронический сценарий болезни отсутствует. Корни уравнения (7) имеют вид

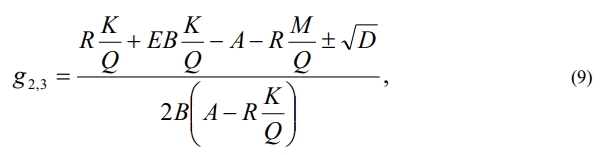
соответствующие значения a_2,3 находятся из соотношения (4) подстановкой g_2,3 из (9).

Устойчивость стационарных точек

а) Стационарная точка (0,0).

В окрестности точки (0,0) линеаризованная система (2) имеет вид

(10)

с матрицей

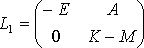(11)

Так как Е>0, то условие устойчивости (10) принимает вид det L₁>0, т.е. E(K-M)<0 или М>K, при этом t₂ L₁<0. Далее предполагаем, что это условие выполняется.

б) Стационарные точки (a_2,3, g_2,3).

Численные эксперименты показывают, что при всех значимых параметрах а₃ g₃равны нулю, поэтому будем рассматривать только стационарную точку (a₂, g₂), что соответствует знаку "+" в (9). Обозначая через a(t) и g(t) возмущения в окрестности стационарной точки (a₂, g₂) получим из (2)

Линейная часть (12) определяется матрицей

(13)

Устойчивость матрицы (13) определяется следующими неравенствами

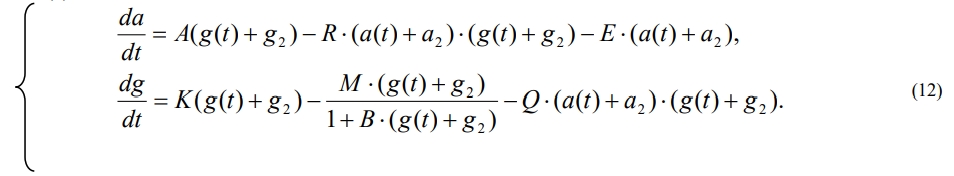
t₂L₂<0, det L₂>0. (14)

Отсюда

т.е.

(15)

Второе условие принимает вид:

(16)

По терминологии ДЛВ-модели, иммунная система имеет "сильный" специфический иммунитет", если выполнено неравенство AQ>RK. Однако, как видно из (16) этого условия еще не достаточно для выполнения второго неравенства в (14). Мы потребуем дополнительно выполнение неравенства

R>BE, (17)

которое означает, что антитела гибнут в основном за счет из взаимодействия молекулами антигена, а не путем естественной гибели. Будем называть такое свойство специфической активностью иммунной системы. Таким образом, далее будем предполагать, что рассматриваемая система обладает сильным специфическим иммунитетом и специфической активностью к антигену HBV. Если эти условия выполнены, то неравенство (16) выполнено и нам остается выяснить алгебраическую структуру условия (15). Из (17) и (15) получим

(18)

Отсюда

(19)

Выполнение неравенства (19) достаточно для выполнения (15).

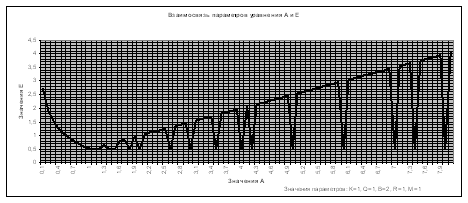
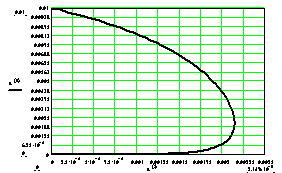
Рисунок 1 - Область устойчивости при K=1, Q=1, B=2, R=1, M=1.

На рисунке 1 представлен пример результатов численных экспериментов по визуализации области устойчивости в координатах (А, Е) при различных значения остальных параметров.

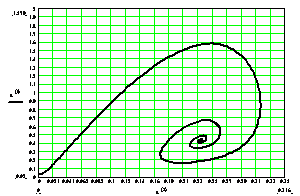
Рисунок 2 - Хроническая форма гепатита В; устойчивая стационарная точка.

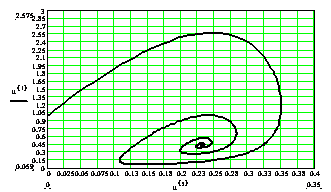
Рисунок 3 - Острая форма гепатита В; неустойчивая стационарная точка.

(а)

(б)

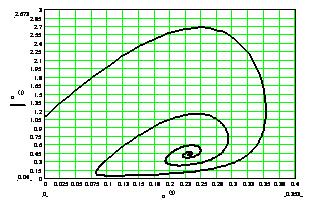
Рисунок 4 - Траектории динамической системы на фазовой плоскости. Вертикальная ось - концентрация антигена HBV, 10⁶ частиц/мл; горизонтальная ось - концентрация специфических антител, 10⁴ частицы/мл. При различных начальных данных и значениях параметров: a(0)=0, А=0.5, Е=0.5. а) g(0)=0.01, б) g(0)=0.02.

(а)

(б)

Рисунок 5 - Траектории динамической системы на фазовой плоскости. Вертикальная ось - концентрация антигена HBV, 10⁶ частиц/мл; горизонтальная ось - концентрация специфических антител, 10⁴ частицы/мл. При различных начальных данных и значениях параметров: a(0)=0, А=0.5, Е=0.5. а) g(0)=1, б) g(0)=1.1. Хроническая форма гепатита В.

Рисунки 4-5 - это численное моделирование динамики вируса HBV и антител для случаев различных значений параметров соответствующих выздоровлению и появлению хронической формы болезни.

Проведенные численные эксперименты позволяют сделать следующий вывод: выполнение свойств специфической активности (17) и сильного специфического иммунитета делает организм стойким по отношению к вирусу гепатита В, переводя сценарий острой формы заболевания, приводящий к летальному исходу, в спиралевидную форму траектории соответствующей хроническому варианту болезни, что демонстрируют рисунки 2-3.

Отсюда следует, что применение лекарственны средств, в частности вакцины и адъювантов, должно быть в первую очередь направлено на обеспечение устойчивости обеих стационарных точек с (2), т.е. на выполнение неравенств:

М>K, QA>RK, R>BE. (20)

Линейное приближение в задаче оптимального управления процессом лечения больных хроническим гепатитом В

Из рисунка 6 понятно, что хроническая форма заболевания представляется спиралевидной кривой в пространстве координат (a, g, t) "наматывающейся" на ось «стационарное состояние».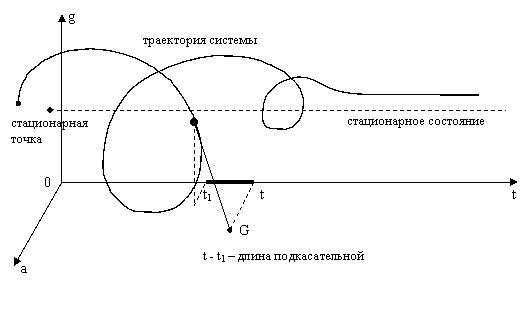

Рисунок 6 - Проекция подкасательной на ось времени.

Вектор касательной к рассматриваемой кривой (a(t), g(t), t) в момент времени t имеет вид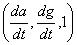

, а касательная прямая, направленная вдоль этого вектора определяется следующими уравнениями:

(21)

Найдем точку пересечения этой прямой с плоскостью g = 0. Из второго уравнения (21) получим

(22)

где через t₁ обозначена координата по оси t точки пересечения касательной с плоскостью g=0 (на рис. 6 это точка G). Заметим теперь, что величина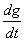

определяется исходной системой дифференциальных уравнений (2). Поэтому, из второго уравнения (2) и (22) получим, что

(23)

отсюда

(24)

Таким образом, минимум величины t₁-t соответствует минимуму величины

. Производная знаменателя в (24) дает следующее условие экстремума:

(25)

Подставляя в (25) значение производных из исходной системы (2), получаем:

(26)

(27)

Уравнение (27) определяет кривую четвертого порядка в фазовом пространстве рассматриваемой динамической системы (плоскость (a,g)).

Обозначим

В этих обозначениях уравнение (27) приобретает такой вид:

(28)

(29)

Далее находим точки пересечения алгебраической кривой, найденной выше, и фазового портрета, соответствующего рассматриваемой динамической системе. Эти точки определяют значения (a, g) при которых надо делать инъекции. Зная указанные точки можно найти соответствующие моменты времени.

Эти моменты времени интересны тем, что касательные в этих точках кривой (a(t), g(t), t) более быстро пересекают плоскость g = 0 (полное уничтожение антигена). Иными словами, в линейном приближении, именно в эти моменты времени организм быстрее всего может выздороветь. Поэтому, естественно предложить применение вакцины усиленной высокомолекулярными адъювантами в указанные моменты времени. Применение данных лекарственных препаратов в несколько раз увеличивает величину А - коэффициент, определяющий скорость воспроизводства специфических антител в результате реагирования на присутствие поверхностного фрагмента вируса HB_SAg, так как этот фрагмент содержится в вакцине, и заметно снижает величину Е - коэффициент, определяющий скорость естественной гибели специфических к данному вирусу антител, за счет присутствия адъюванта.

Список литературы / References

Дибров Б.Ф., Лившиц М.А., Волькенштейн М.В. Математическая модель иммунной реакции // Биофизика. - том 21, № 5, 1976. - С. 905 - 909.
Дибров Б.Ф., Лившиц М.А., Волькенштейн М.В. Математическая модель иммунной реакции. Стохастические аспекты // Биофизика. - том 22, № 2, 1977. - С.313 - 317.
Дибров Б.Ф., Лившиц М.А., Волькенштейн М.В. Математическая модель иммунной реакции // Биофизика. - том 23, № 1, 1978. - С. 143 - 148.
Дибров Б.Ф., Лившиц М.А., Волькенштейн М.В. Математическая модель иммунной реакции. Пороговый характер инфекционного процесса // Биофизика. - том 23, № 3, 1978. - С. 494 - 499.