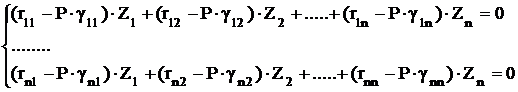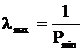PROBLEMS OF CALCULATION OF FARMS AND TRELLISED SYSTEMS ON STABILITY

Сон М.П.

Кандидат технических наук, Пермский национальный исследовательский политехнический университет

ПРОБЛЕМЫ РАСЧЕТА ФЕРМ И РЕШЕТЧАТЫХ СИСТЕМ НА УСТОЙЧИВОСТЬ

Аннотация

Если задаться функциями прогиба в задачах устойчивости такими же, как в задачах статики, без учета продольных сил, получим более простой вариант решения. Такая замена точных решений приближенными  дает решение с удовлетворительной точностью, когда критическое значение продольной силы в элементе сильно меньше критической силы в основной системе метода перемещений, и некорректный  результат в противоположном случае. Показанная методика является простейшим вариантом метода конечных элементов (МКЭ) применительно к исследованию устойчивости стержневых систем. В данной статье приводится анализ проблем связанных с расчетом устойчивости шарнирно-стержневых систем МКЭ. Показаны причины неточности расчетов и способы достижения адекватных решений.

Ключевые слова: устойчивость, ферма, метод конечных элементов, программные комплексы.

Son M. P.

 PhD in Engineering, Perm national research polytechnical university

PROBLEMS OF CALCULATION OF FARMS AND TRELLISED SYSTEMS ON STABILITY

Abstract

Considering deflection function in stability problems like in statics problems, excluding longitudinal forces, we could achieve a simpler version of the solution. This replacement of precise solution with approximate one provides the solution with reasonable accuracy when the critical value of the longitudinal force in the element is much less than the critical force in the main system of displacement method and the incorrect solution otherwise. The illustrated method is the simplest version of the finite element method (FEM) applied to the research of the stability of bar systems. This paper  provides an analysis of the problems related to the calculation of stability of hinged-rod FEM systems. The reasons for the calculations inaccuracies and ways to achieve adequate solutions are shown.

Keywords: stability, farm, final elements method, program complexes.

Зададим  форму потери устойчивости с точностью до нескольких параметров 

                      (1)

Где  - функции только от х, удовлетворяющим некоторым или всем граничным условиям стержня

При исследовании устойчивости стержневых систем в качестве неизвестных параметров, входящих в (1) и характеризующих деформации системы можно принять перемещения и углы поворота узлов системы, а также (при необходимости) отдельных сечений стержней. Задаваясь формой изгиба стержней, можно избежать применения специальных трансцендентных функций и свести задачу определения критической силы к виду (2).

                   (2)

Где ,                                               (3)

Если стержни системы имеют постоянную жесткость, то можно, приняв в качестве формы изгиба те же функции формы, что и в задачах статики, получить для элементов   и  простую механическую и геометрическую трактовку.

В классическом методе перемещений для расчета на устойчивость влияние продольной силы учитывалось путем умножения реакций  на специальные функции , но если задаться функцией прогиба y(x) от поворота и линейного смещения на безразмерные единицы   такие же, как в задачах статики, без учета продольной силы, то коэффициенты метода перемещений примут следующий вид:

                                                                  (4)

Или в матричном виде: 

Соответственно уравнения энергетического метода (5)

Определяя минимальный параметр P при котором система имеет не нулевое решение Z, получаем приближенное, несколько завышенное значение критической нагрузки и форму потери устойчивости. P_кр можно определить: либо раскрывая определитель матрицы, либо вычисляя матрицу податливости как обратную матрицу жесткости. Уравнение (5) эквивалентно равенству

, где , .

Найти  и соответствующего собственного вектора перемещений с использованием современных ЭВМ не является проблемой [3].

Изложенная форма энергитического метода, предложенная в работах В.В. Болотина [4] при выборе в качестве неизвестных узловых перемещений, может быть также получена, согласно А.Р. Ржаницину, простым разложением специальных функций  метода перемещений  в ряды с удержанием первых двух членов ряда.

Такая замена точных решений приближенными  дает удовлетворительное решение при достаточно малых значениях Ni (продольных сил), когда критическое значение N_iкр меньше критической силы в основной системе метода перемещений (!), и неудовлетворительный результат в противоположном случае.

Показанная методика является простейшим вариантом метода конечных элементов применительно к исследованию устойчивости стержневых систем. Устойчивость равновесия образует сложный и порой противоречивый раздел строительной механики [5]. Современные программные комплексы, реализующие метод конечных элементов порой допускают те же самые ошибки. Покажем это на следующем примере: рама (рис.1.) жесткости всех элементов EI, размеры (высота и длины пролетов) l.

Рис. 1. рама (стержневая конструкция)

Из аналитического решения показанной рамы получим: , но если мы возьмем основную систему метода перемещений (закрепим от поворота узлы рамы), то две стойки будут работать как стержни с двумя жесткими заделками, для которых критическая сила равна .  Поскольку значение критических сил близко,то согласно (!) мы можем получить некорректное решение. Рассмотрим результаты решение задачи (рис.2.), выполненной в ПК “Лира” (для удобства EI=1, l=1).

Рис. 2. Результаты расчета рамы на устойчивость

Видно, что критическая сила найденная расчетом в программном комплексе равна , что соответствует форме потери устойчивости для основной системы метода перемещений. Для получения точного решения необходимо соблюдение (!), этого можно добиться путем установки более густой сетки конечных элементов, так, например, при разбиении стоек пополам мы увеличим критическую силу для основной системы метода перемещений в 4 раза, т.к. она обратно пропорциональна квадрату длины. Таким образом (!) соблюдается, и мы приходим к верному решению (рис. 3.).

Рис.3. Результаты расчета рамы на устойчивость, при дроблении стоек пополам

Аналогичные проблемы будут возникать и при расчете ферм, представляющих собой совокупность шарнирных треугольников, т.к. основная система метода перемещений для них совпадает с исходной схемой.

Рассмотрим устойчивость шарнирно-опертого сжатого стержня, состоящего из двух ветвей, соединенных между собой решеткой. Исходные данные: h=11м, EI=50кНм², EF=10МН. Очевидно, что критическая сила зависит не только от сечения ветвей, но и от сечений соединительной решетки, и от ее способа соединения с ветвями.

Рис.4. Шарнирно-стержневая система

Выполним расчет фермы (рис.4.) на вертикальную нагрузку Vв ПК «Лира», при этом проанализируем изменение критической силы в зависимости от способов соединения ее элементов между собой. Получим. При жестком соединении всех элементов , при жестких стойках с шарнирно прикрепленной решеткой: , при шарнирном соединении всех элементов: . Результаты такого расчета парадоксальны при ослаблении фермы (путем введения шарниров) и уменьшения ее жесткости мы получаем увеличение критической силы. Причиной этого парадокса является (!), так  ничто иное, как критическая сила для отдельного элемента пояса фермы. Для получения адекватного результата необходимо разбить элементы фермы на несколько частей (что обычно не делается в расчетных моделях). Результаты расчета сведены в таблицу 1.

Таблица 1. Результаты расчета фермы на устойчивость

Условие соединение решетки	, без разбиения стержней фермы, кН	, с разбиением стержней фермы на два КЭ, кН	Приближенное решение согласно [1], кН
Жесткое	374	374	350
Стойки с шарнирной решеткой	484	364
Шарнирное	987	358

Точный расчет на устойчивость составных стержней разработан проф. А.Р. Ржаницыным и весьма полно изложен в его книге [2].

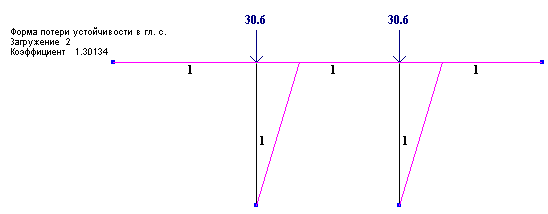
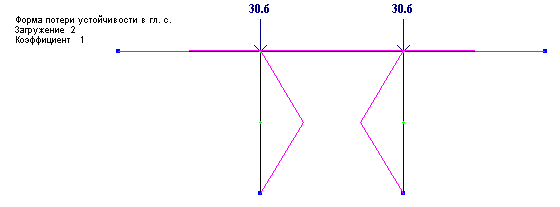
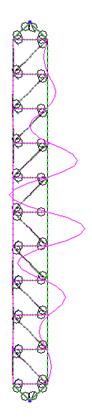
Необходимо отметить, что при расчете фермы (рис.4.) на горизонтальную нагрузку G, решения при дроблении стержней на более густую сетку КЭ не дает заметных расхождений. Но сгущение целесообразно для лучшего понимания форм потери устойчивости (рис.5.).

Рис.5. потеря устойчивости сжатого пояса фермы от горизонтальной нагрузки

На реальные фермы и колонны с решеткой,  и подобные конструкции действуют горизонтальные и вертикальные силы, поэтому, в случае анализа критических сил и форм устойчивости, необходимо дробление сжатых элементов на несколько частей.

Литература

1. Основы расчета сооружений на устойчивость./ Раевский А.Н. /Высшая школа 1962
2. Устойчивость равновесия упругих систем./Ржаницын А.Р./ Гостеортехиздат 1955
3. Расчетные модели сооружений и возможность их анализа. /Перельмутер А.В., Сливкер В.И./ ДМК пресс 2007
4. Болотин В.В./ О вариационных принципах теории упругой устойчивости./ Проблемы механики твердого деформируемого тела./ Судостроение 1973, с.83-88
5. Устойчивость равновесия конструкций и родственные проблемы. Том 1./Перельмутер А.В., Сливкер В.И./ СКАД СОФТ 2007

References

1. Osnovyraschetasooruzheniynaustoychivost'./Raevskiy A.N. /Vysshayashkola 1962
2. Ustoychivost' ravnovesiyauprugikhsistem./Rzhanitsyn A.R./ Gosteortekhizdat 1955
3. Raschetnyemodelisooruzheniyivozmozhnost' ikhanaliza. /Perel'muter A.V., Slivker V.I./ DMK press 2007
4. Bolotin V.V./ O variatsionnykhprintsipakhteoriiuprugoyustoychivosti./ Problemymekhanikitverdogodeformiruemogotela./ Sudostroenie 1973, s.83-88
5. Ustoychivost'ravnovesiyakonstruktsiyirodstvennyeproblemy. Tom 1./Perel'muter A.V., Slivker V.I./ SKAD SOFT 2007