TO THE STUDY OF THE BEHAVIOUR OF TRAJECTORIES OF POINT MAPPING BETWEEN PLANES IN REMOTE PARTS OF THE PHASE PLANE
TO THE STUDY OF THE BEHAVIOUR OF TRAJECTORIES OF POINT MAPPING BETWEEN PLANES IN REMOTE PARTS OF THE PHASE PLANE
Abstract
The question of ‘infinity stability-instability’ is an important issue in the study of the dynamics of a system in the plane. In this work, to solve this question, a methodology for analysing the behaviour of trajectories of a point mapping between planes is proposed, using a substitution of variables that translates the plane into the interior of a circle of unit radius (i.e., an infinitely distant part of the plane into a finite one). On the example of studying specific quasilinear systems, the expediency of using the suggested methodology to obtain a clear picture of the behaviour of the trajectories of the point mapping on the entire phase plane, including its remote parts, is shown. It is noted that the use of the indicated replacement allows to confirm the earlier research of the influence of the character of nonlinearity on the results of the qualitative study of systems with small parameter at nonlinear terms by asymptotic methods.
1. Введение
Известно, что в основе наиболее эффективного подхода к исследованию тех задач теории нелинейных колебаний , в которых классические методы оказываются малоэффективными, лежит метод точечных отображений , в последние годы все шире и чаще привлекающийся как для рассмотрения общих вопросов теории динамических систем, так и для решения различных прикладных задач. Следует отметить, что изучение многих типов динамических систем может быть сведено к построению и исследованию точечного преобразования некоторого множества в себя. То есть задачу изучения динамической системы можно разбить на два основных этапа. Целью первого этапа является выбор некоторого геометрического образа (прямой, плоскости, пространства или какой-то то их части), к изучению точечного отображения которого в себя сводится изучение системы. На втором этапе строится точечное отображение в явном виде, если это возможно. Если получение его в явном виде невозможно или затруднительно, то применяются приближенные (в том числе и асимптотические) методы, а также те или иные численные методы. И вместо исходной динамической системы исследуется соответствующее ей точечное отображение, и уже по поведению его траекторий делаются выводы о поведении динамической системы при тех или иных значениях параметров.
2. Основная часть
Применение метода точечных отображений для построения математических моделей дискретных систем второго порядка, а также его использование при исследовании непрерывных систем на плоскости, предоставляет возможность получения адекватной информации о динамике систем математическими методами .
При изучении качественной картины поведения траекторий точечных отображений в конкретных задачах большую роль играет исследование поведения траекторий в удаленных частях фазовой плоскости. Существует математический аппарат, позволяющий решать задачу, совершив замену переменных, которая перевела бы бесконечно удаленную часть плоскости в конечную. Этого, например, можно достичь с помощью преобразования Бендиксона .
;
,
которое переводит бесконечно удаленные точки плоскости x0, y0 в начало координат плоскости u0, v0. Удобно пользоваться также преобразованием Пуанкаре , переводящим плоскость x0, y0 на сферу радиуса 1, касающуюся плоскости x0, y0 в начале координат
,
,
где τ0 есть тангенс направления на исследуемую точку. Координатные линии z0=const и τ0=const суть на плоскости прямые, параллельные оси y, и прямые, проходящие через начало координат. На сфере же они являются большими кругами, проходящими через взаимно перпендикулярные диаметры. Рассмотрение производится на плоскости τ0, z0, касательной к сфере, куда точки сферы проектируются из ее центра.
Заметим, что не менее удобным при исследовании поведения траекторий точечного отображения в удаленных частях плоскости может быть использование замены переменных .
непосредственно переводящей плоскость x0, y0 во внутренность круга единичного радиуса u02+v02<1 (при этом бесконечно удаленным точкам плоскости соответствует окружность единичного радиуса u02+v02=1). Заметим, что отображения (1) и (2) являются взаимно-непрерывными и взаимно-однозначными, т.к. их якобианы отличны от нуля. Исключение для (2) составляют точки окружности u02+v02=1. При этом, поскольку
,
,
то направление на исследуемую точку при замене (2) остается неизменным, изменение претерпевает лишь расстояние до нее от начала координат (при x0=y0=0 u0=v0=0).
примут вид
а значит при
. Доопределив (4) на окружности по правилу
в случае существования соответствующих пределов, получим точечное отображение единичного круга в себя, качественное поведение траекторий которого отражает качественное поведение траекторий исходного отображения (3) в конечной части плоскости x0, y0, причем поведение траекторий (4) в окрестности окружности
отражает поведение траекторий (3) в удаленных частях плоскости, при этом картина обладает большей наглядностью .
Для примера рассмотрим следующие системы.
1. Уравнение Дуффинга
где 0<μ<<1, A>0. Известно , что исследование поведения траекторий (5) может быть сведено к изучению поведения траекторий точеного отображения
с точностью до величин порядка μ2 приближающего точечное отображение, порождаемое траекториями соответствующей (5) системы на секущей поверхности .
В переменных u0, v0 точечное отображение (6)-(7) примет вид
допускающий численное исследование траекторий на всем множестве .
Окружность является инвариантным многообразием (8). В точках этой окружности
Таким образом, любая точка окружности является неподвижной точкой отображения
(т.е. каждой такой точке соответствует цикл 4 порядка отображения
— рисунок 1 — а именно:
). А вопрос об устойчивости окружности
легко решается посредством сравнения величин
и
вблизи окружности (
).
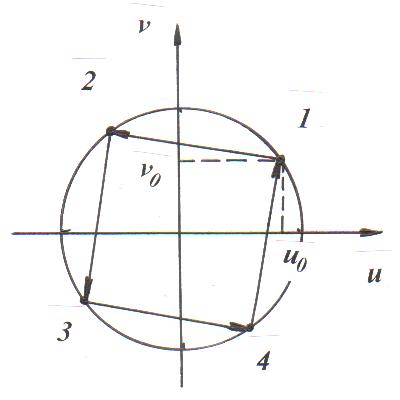
Рисунок 1 - Поведение точечного отображения на окружности u02+v02=1 в случае уравнения Дуффинга
2. Уравнение синхронизуемого осциллятора с нелинейностью вида кубической параболы:
где 0<μ<<1, A>0. Известно , что исследование поведения траекторий (5) может быть сведено к изучению поведения траекторий точеного отображения
с точностью до величин порядка μ2 приближающего точечное отображение, порождаемое траекториями соответствующей (10) системы на секущей поверхности t=[t/(2π)]2π.
В переменных u0, v0 точечное отображение (11)-(12) примет вид
допускающий численное исследование траекторий на всем множестве .
Окружность является инвариантным многообразием (8). В точках этой окружности
Таким образом, любая точка окружности является неподвижной точкой отображения
(т.е. каждой такой точке соответствует цикл 2 порядка отображения
– рисунок 2 — а именно:
). А вопрос об устойчивости окружности
легко решается посредством сравнения величин
и
вблизи окружности (
).
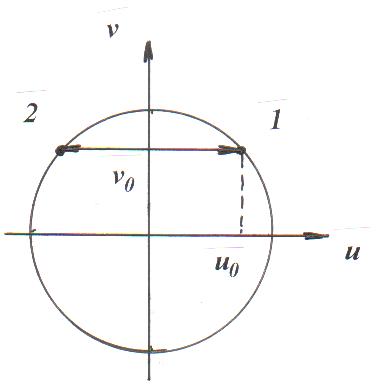
Рисунок 2 - Поведение точечного отображения на окружности u02+v02=1 в случае нелинейности типа кубической параболы
3. Уравнение синхронизуемого осциллятора с типа Ван-дер-Поля :
где 0<μ<<1, A>0. Известно
, что исследование поведения траекторий (15) может быть сведено к изучению поведения траекторий точеного отображенияс точностью до величин порядка μ2 приближающего точечное отображение, порождаемое траекториями соответствующей (15) системы на секущей поверхности .
В переменных u0, v0 точечное отображение (11)-(12) примет вид
допускающий численное исследование траекторий на всем множестве .
Окружность является инвариантным многообразием (18). В точках этой окружности
т.е. отображение на окружности является тождественным.
Численное исследование поведения траекторий (19) показало, что всегда является притягивающим множеством (что подтверждает результаты статьи об «устойчивости бесконечности» в случае полиномиальной нелинейности системы).
4. Уравнение квазигармонического осциллятора с квадратичным трением .
где 0<μ<<1, A>0. Известно , что исследование поведения траекторий (20) может быть сведено к изучению поведения траекторий точеного отображения
с точностью до величин порядка μ2 приближающего точечное отображение, порождаемое траекториями соответствующей (20) системы на секущей поверхности .
В переменных u0, v0 точечное отображение (21)-(22) примет вид
допускающий численное исследование траекторий на всем множестве .
Окружность является инвариантным многообразием (23). В точках этой окружности
Таким образом, любая точка окружности является неподвижной точкой отображения
(т.е. каждой такой точке соответствует цикл 2 порядка отображения
– рисунок 3 – а именно:
). А вопрос об устойчивости окружности
легко решается посредством сравнения величин
и
вблизи окружности (
).
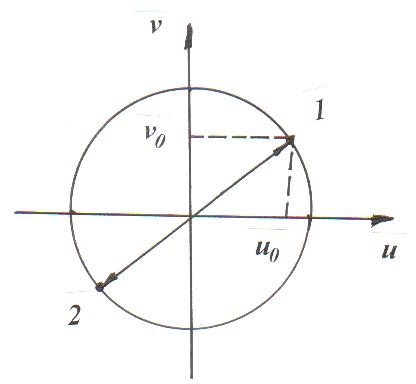
Рисунок 3 - Поведение точечного отображения на окружности u02+v02=1 в случае квадратичного трения в системе
5. Уравнение синхронизуемого осциллятора с нелинейностью вида sgn
где 0<μ<<1, A>0. Известно , что исследование поведения траекторий (20) может быть сведено к изучению поведения траекторий точеного отображения .
В этом случае точечное отображение (26)-(27) в переменных u0, v0 примет вид
допускающий численное исследование траекторий на всем множестве . Окружность
является инвариантным многообразием (28)-(29). В точках этой окружности
а т.к. то можно ввести обозначения
,
, а (30)-(31) переписать как
где
Т.е. отображение (30)-(31) на окружности есть
или отображение поворота на угол -α*. Таким образом, условия ,
могут выполняться только если ξ=0, μπ<0, причем отображение становится тождественным. Отображение (34) может иметь циклы порядка n∈N только если существует такое m∈N, что nα*=2πm. Скажем, цикл порядка n=2 может существовать при ξ=0, μπ>1 (при этом отображение (34) таково, что
является тождественным отображением на окружности u02+v02=1).
Численное исследование поведения траекторий (30)-(31) показало, что в случае существования устойчивой неподвижной точки областью ее притяжения является все множество u02+v02<1 . В случае, когда неподвижных точек у (30)-(31) нет, либо они неустойчивы, но 0<μπ<<1, у отображения (30)-(31) всегда существует устойчивое многообразие при u02+v02<1, все более расширяющееся при |ξ|→|ξac| . Таким образом, в случае существования устойчивой неподвижной точки (25) областью ее притяжения является все фазовое пространство. При |ξ|→|ξac| у отображения (25) всегда существует притягивающее множество в конечной части плоскости, областью притяжения которого является все фазовое пространство. При |ξ|→|ξac| все траектории (25), отличные от существующих неподвижных точек, уходят в бесконечность . Следует также отметить, что изучение поведения траекторий
посредством перехода к переменным u0, v0 позволяет установить факт рождения устойчивой инвариантной кривой при переходе через границу Nφ и ее ухода в бесконечность при |ξ|→|ξac|.
Следует отметить, что предложенный выше подход к исследованию поведения траекторий точечного отображения позволил на только подтвердить, но и уточнить полученные результаты.
3. Заключение
В работе рассмотрена методика изучения поведения траекторий двумерного точечного отображения в удаленных частях фазовой плоскости, основанная на отображении всех точек фазовой плоскости внутрь круга единичного радиуса. Это отображение является взаимно однозначным для точек конечной части плоскости, поэтому выводы о поведении траекторий системы обладают не только наглядностью, но и достоверностью , а методика позволяет не только решать вопрос об «устойчивости или неустойчивости бесконечности», но и оценивать характер поведения траекторий в целом. Предложенная методика апробирована на примере изучения отображений, описывающих реальные динамические системы. Динамика рассмотренных систем в конечно части плоскости ранее была рассмотрена в работах , , , . Поэтому приведенное выше исследование является дополнением и уточнением исследований, проведенных ранее.