NUMERICAL SIMULATION OF GAS MICROFLOWS
NUMERICAL SIMULATION OF GAS MICROFLOWS
Abstract
The paper considers numerical simulation of unsteady gas flow through a microscopic hole into a space filled with an equilibrium gas, taking into account the effects of strong nonequilibrium and sparsity.
The kinetic Boltzmann equation for the distribution function in the form of BGC is solved by the method of discrete velocities. Integration of a non-stationary equation in time within one time step allows us to obtain an algebraic formulation representing the process of evolution of the system in the form of a sequence of flights and collisions.
The main results of calculations are presented in the form of graphical distributions that clearly demonstrate the course of the microjet flow depending on the gas rarefaction parameter. The Compaq Visual Fortran programming environment is used for modeling.
1. Введение
Микротехнологии и современные материалы открывают перед исследователями новые возможности, новые направления исследования. В области гидрогазодинамики сформировавшимся новым направлением является микрофлюидика – исследование течения жидкости и газа в микромасштабах. При проектировании и создании устройств, основанных на микротечениях различного направления, необходимо прежде всего знать законы течения жидкости и газа на микро- и наноуровне.
Технологическим применением микроструй является смешение газов и защита поверхностей от воздействия химически агрессивной или высокотемпературной среды, осуществление процесса охлаждения. В настоящее время наиболее интенсивно развиваются численные методы исследования микротечений, позволяющие детально понять природу течений в микросистемах
, , . При этом особенности течения газовой среды определяются числом Кнудсена Kn – отношением длины свободного пробега молекул газа λ к характерному размеру системы L:Для микротечений, когда характерный размер системы L сравним с длиной свободного пробега λ, число Кнудсена , нарушаются условия применимости модели сплошной среды, и уравнения Навье-Стокса не работают должным образом. В данном случае для описания системы необходимо использовать кинетическое уравнение Больцмана
В работе рассматривается нестационарное истечение газа через отверстие в пространство, заполненное равновесным газом с учетом эффектов сильной неравновесности и разреженности.
2. Постановка задачи
Рассмотрим цилиндрическую расчетную область пространства высотой H и радиусом R вблизи отверстия радиусом в твердой стенке, через которое происходит истечение газа (рис. 1). Ось цилиндра z совпадает с центром отверстия O.
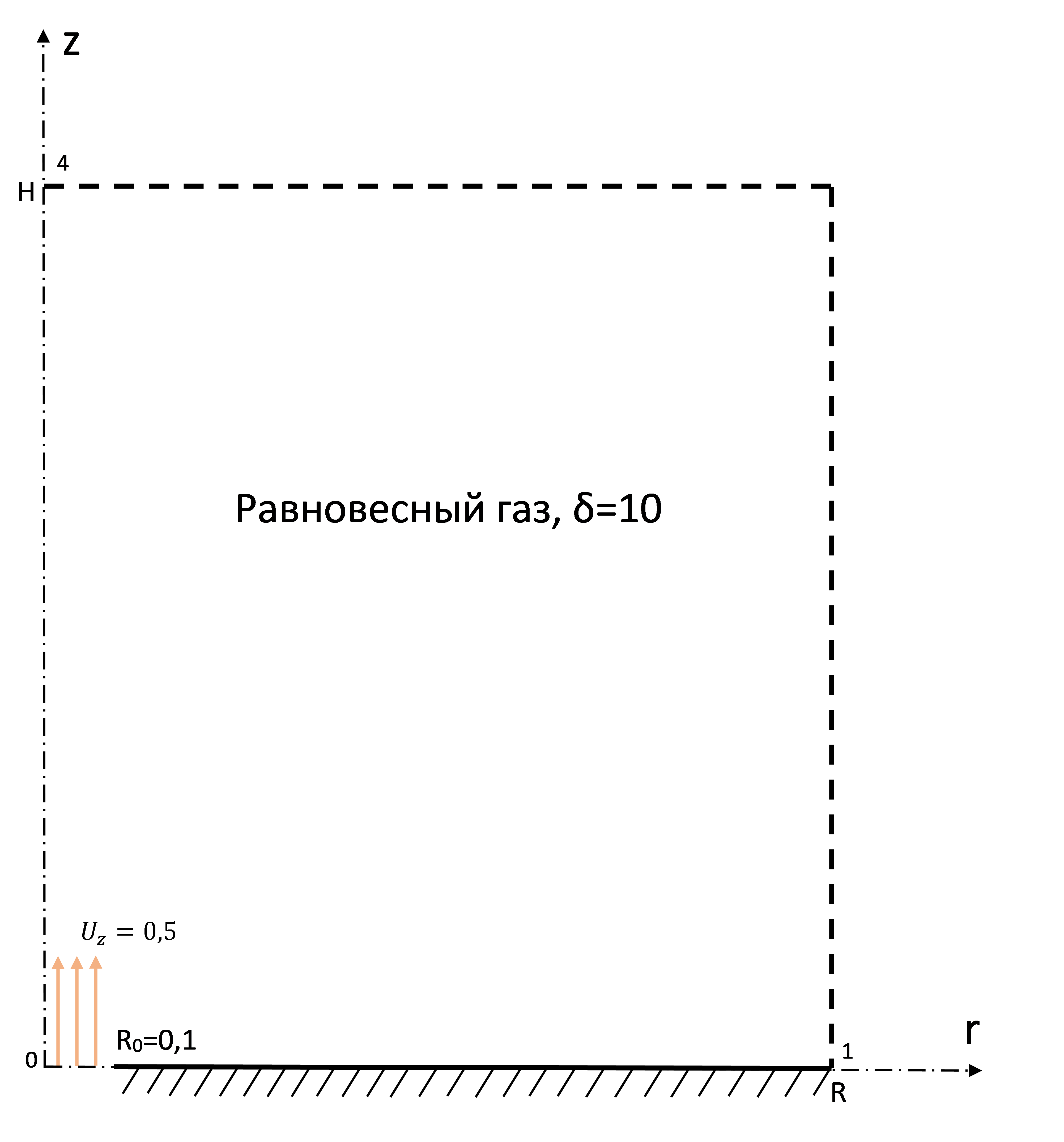
Рисунок 1 - Схематичное представление задачи
где P – давление, – коэффициент вязкости, – наиболее вероятная скорость газовых молекул массой m при температуре T.
Граничные условия:
1. Снизу расчетная область ограничена твердой стенкой с микроотверстием. На непроницаемой поверхности стенки для функции распределения задаются условие диффузного рассеяния. Верхняя и боковая границы – проницаемы для молекул газа, при этом функция распределения для влетающих в расчетную область молекул принимается локально-равновесной. Функция распределения вылетающий молекул на этих границах рассчитывается с помощью экстраполяции из объема.
2. В плоскости отверстия задается локальная-равновесная функция распределения с заданной средней скоростью истечения газа.
3. Температура на всех границах задана и поддерживается постоянной.
Исследуются различные режимы течения, соответствующие различным параметрам разреженности среды.
3. Методика расчета
3.1. Уравнение Больцмана
Нестационарное уравнение Больцмана позволяет найти функцию распределения, то есть определить плотность вероятности для частиц газа иметь определённые скорости в произвольный момент времени в любой точке пространства. В свою очередь знание функции распределения дает возможность вычислить все локальные макроскопические величины (плотность, температуру, среднюю скорость течения и др.) , , .
Простейшей моделью столкновений для уравнения Больцмана является модель Бхатнагара-Гросса-Крука (БГК) :
где – функция распределения в точке пространства,
– полная скорость частиц газа.
– локально-равновесная функция распреления, к которой стремится
в результате столкновений между частицами за характерное время релаксации
,
где – собственная скорость частиц,
– средняя скорость потока,
– газовая постоянная,
– числовая плотность и
– температура,
3.2. Метод дискретных скоростей (DVM)
В численном расчете необходимо дискретизировать как простанство координат , так и пространство скоростей
. Соответсвенно, уравнение Больцмкана для дискретных скоростей (DVBE) принимает вид:
где – дискретная функция распределения вдоль направления дискретной скорости
.
Вместо интегралов для макропараметров можно записать квадратурные формулы:
где – квадратурный вес.
Интегрирование уравнения Больцмана для дискретных скоростей по времени в течение одного временного шага дает:
где – характерное время столкновительной релаксации в центре рассматриваемой ячейки пространства в момент времени
Таким образом, на каждом временном шаге решение нестационарного уравнения Больцмана может быть приближенно представлено в виде двух последовательных процессов:
1. Процесс перелетов.
2. Процесс столкновений.
Здесь – промежуточная функция распределения в центре пространственной ячейки
в момент времени
. Для того, чтобы получить функцию распределения
, функции
и
должны быть определены заранее.
– это функции распределения в окружающих центрах соседних ячеек, которые могут быть получены с помощью интерполяционных методов:
4. Результаты и обсуждение
На рисунке 2 представлен результат истечения струи со скоростью в область, заполненную газом при
, при этом
. Количество дискретных молекулярных скоростей
, количество дискретных азимутальных углов молекулярной скорости
количество дискретных осевых углов молекулярной скорости
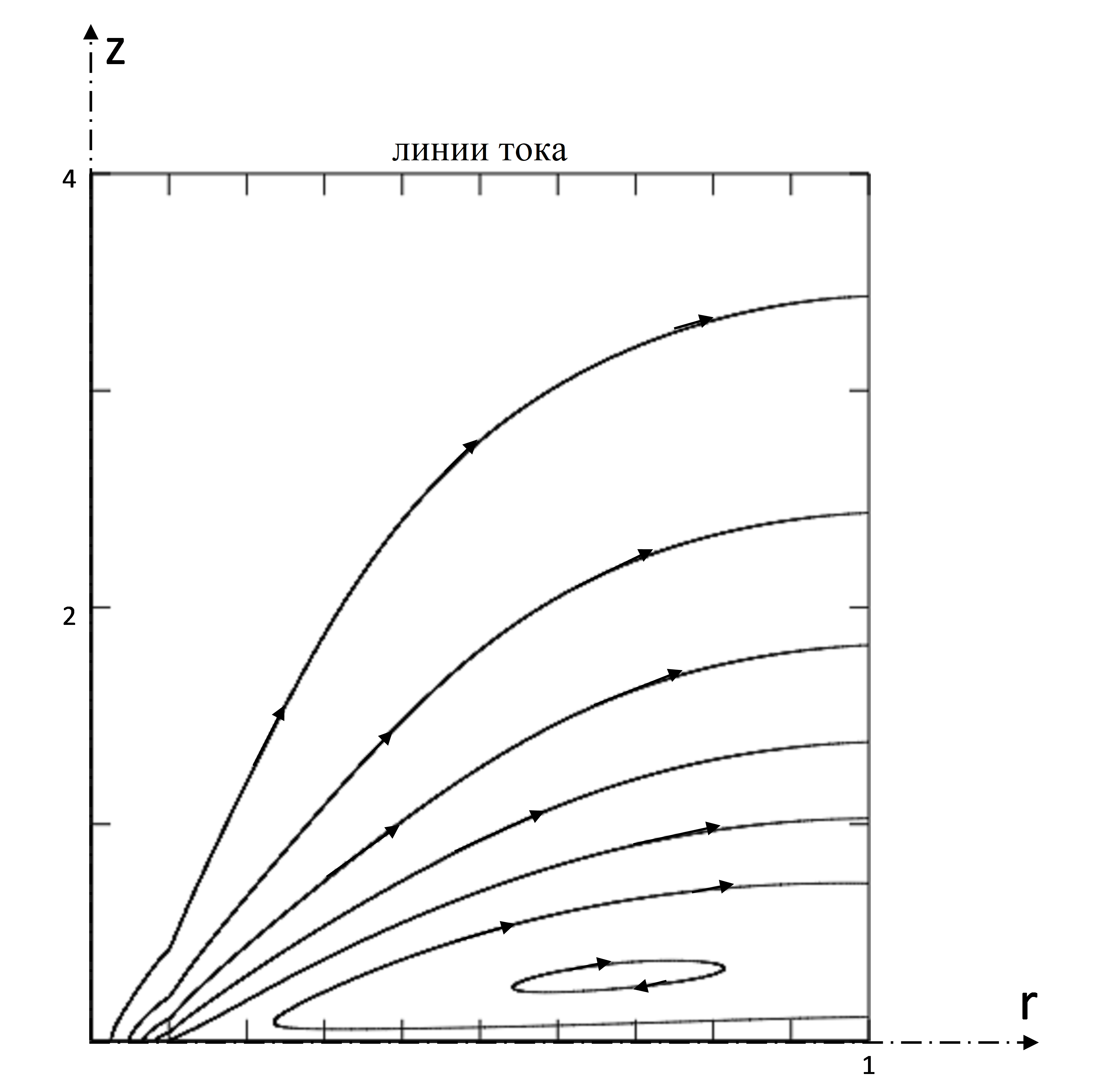
Рисунок 2 - Общий вид линии тока течения при t → ∞
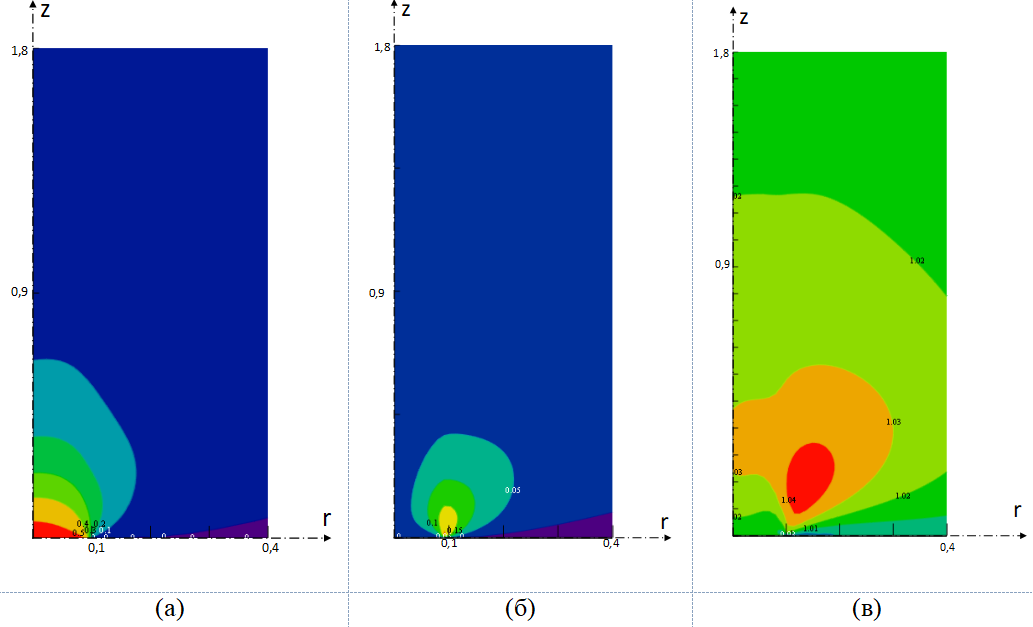
Рисунок 3 - Поле течения струи:
а – графики распределения азимутальной компоненты скорости;
б – графики распределения радиальной компоненты скорости;
в – графики распределения температуры
1. Эффективному смешению газов способствует:
– максимальная скорость потока при невысоких температурах;
– увеличение температуры потока при уменьшении скорости истечения.
2. Охлаждению способствует уменьшение скорости теплового движения частиц, что приводит к снижению скорости распространения струи в пространстве.
Азимутальная скорость снижается с 0,5 до 0,1 в области , поэтому наиболее интенсивное перемешивание при начальной скорости
наблюдается в области z = 0,7 и r = 0,2 (рисунок 3а). Радиальная скорость снижается с 0,5 до 0,15 в области периферии отверстия
(рисунок 3б). Наблюдается зона возвратного течения (т.е. течения вдоль поверхности) со скоростью
в области от r = 0,2 (фиолетовые зоны графика 3а и 3б), что способствует охлаждению. Характерное увеличение температуры составляет 0,05%. Зона наибольшей температуры соответствует красной зоне на графике 3в
минимальная соответствует наиболее вероятной максвелловской температуре
.
5. Заключение
Для большей интенсификации течения необходимо увеличивать скорости течения до сверхзвуковых.
Результаты расчетов течений в микроканалах свидетельствуют, что численное решение модельных кинетических уравнений может быть успешно использовано для моделирования стационарных и нестационарных внутренних течений.
Полученные результаты способствуют пониманию природы течений газа при различных скоростях и параметрах разреженности среды. Результаты исследований могут иметь значение для приложений, в которых встречаются течения газа: в аэрокосмической технике, при разработке МЭМС и многое другое.
