THE STUDY OF THE PEROVSKITE SOLAR CELL PARAMETER INFLUENCE ON THEIR EFFICIENCY BY USING MACHINE LEARNING

Машинное обучение становится все более популярным инструментом для исследований в области материаловедения. При помощи методов машинного обучения можно оптимизировать поиск исходных структур соединений, что способствует созданию новых материалов с определёнными свойствами, их улучшению, ускорению процесса разработки новых инновационных решений, сокращению затрат ресурсов и времени на исследование

Набор данных для обучения алгоритмов машинного обучения для решения задачи поиска наилучших параметров для получения соединения с высокой эффективностью (PCE) был получен при помощи моделирования PSC различной архитектуры (зарядовые слои, перовскиты, толщины перовскитного слоя) в программном пакете SCAPS

Перед непосредственной настройкой алгоритмов и их обучением требуется предварительная обработка набора данных, поскольку полученный набор имеет пропуски в данных. На рисунке 1 представлен фрагмент датасета после обработки.

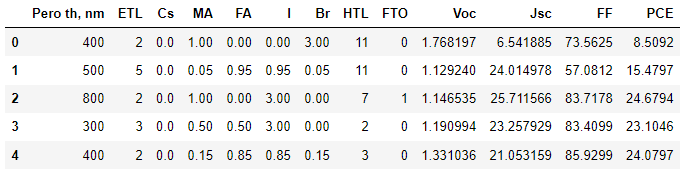
Рисунок 1 - Фрагмент датасета

Примечание: Примечание: Pero th, nm – толщина перовскитного слоя, нм; ETL – тип электронно-транспортного слоя; Cs – количество Cs в А-положении; MA – количество MA в А-положении, FA – количество FA в А-положении, I – количество йода в Х-положении, Br – количество брома в Х-положении, HTL – тип дырочно-транспортного слоя, FTO – присутствие слоя FTO, Voc – напряжение холостого хода, Jsc – ток короткого замыкания, FF – фактор заполнения, PCE – эффективность преобразования энергии

DOI:10.60797/IRJ.2024.143.121.1

Тип зарядово-транспортных слоёв задавался цифрами, кодировка представлена в таблице 1.

Обучение было разбито на два этапа:

1. Решение задачи регрессии (несколько признаков и одна целевая переменная).

2. Решение задачи многоцелевой регрессии (несколько признаков и несколько целевых переменных).

Всего получилось 7182 объекта, которые будут анализироваться по 12 признакам ('Pero th', 'ETL', 'Cs', 'MA', 'FA', 'I', 'Br', 'HTL’, ’FTO’, 'Voc', 'Jsc', 'FF') и 1 целевой переменной ('PCE') для первого этапа, а также по 9 признакам ('Pero th', 'ETL', 'Cs', 'MA', 'FA', 'I', 'Br', 'HTL', ‘FTO’) и 4 целевым переменным ('Voc', 'Jsc', 'FF', 'PCE'), значение которых и будут предсказываться на втором этапе.

Перед загрузкой данных в алгоритм была построена тепловая карта взаимокорреляций Пирсона для признаков (см. рис. 2). Корреляция – важнейший фактор, лежащий в основе анализа данных. Он сообщает, как переменные в наборе данных связаны друг с другом.

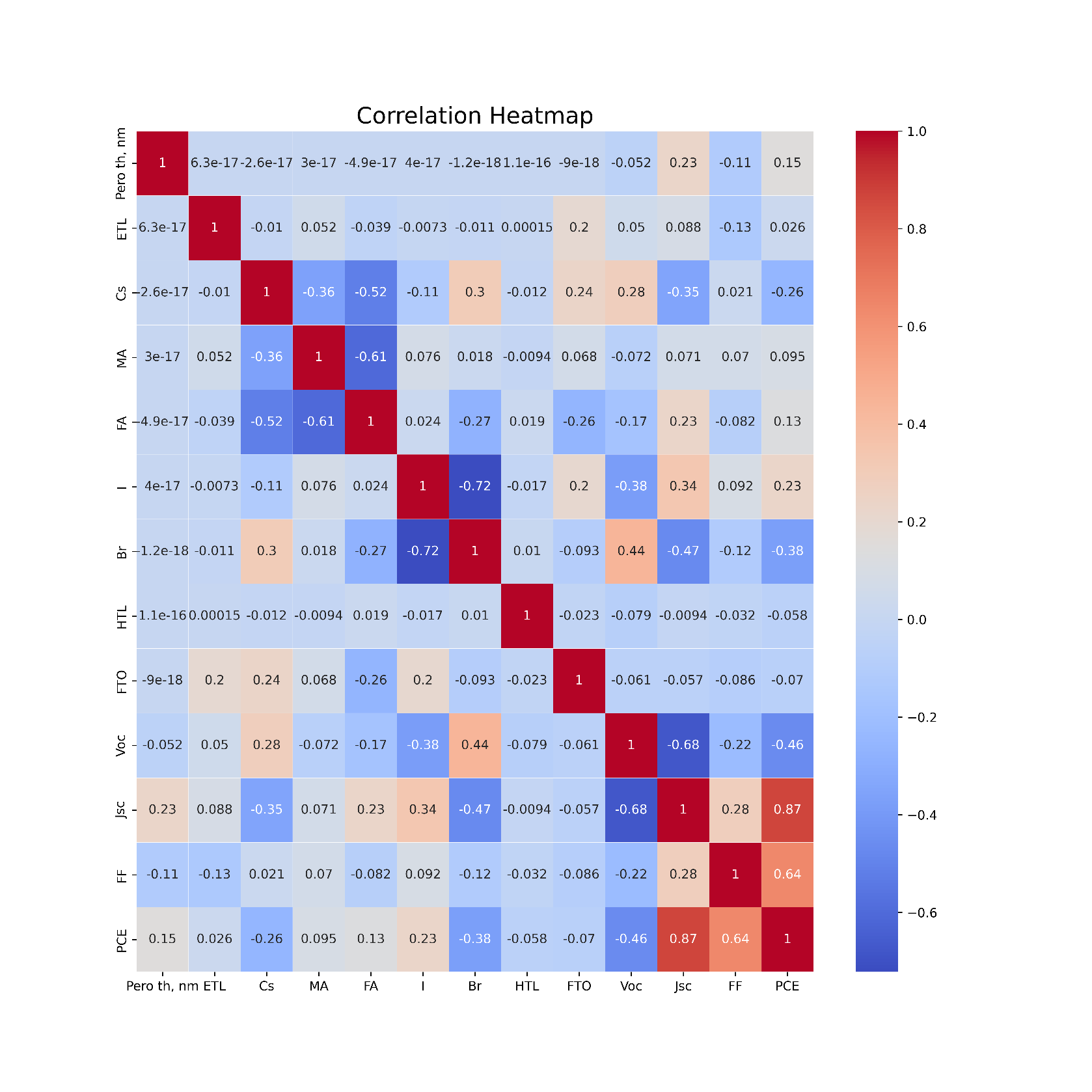
Рисунок 2 - Тепловая карта матрицы корреляции признаков и целевых переменных

DOI:10.60797/IRJ.2024.143.121.3

Поскольку коэффициент корреляции Пирсона обладает несколькими недостатками: работает только с непрерывными переменными, учитывает только линейную связь между ними, чувствителен к выбросам, использовалась Phik (φk) корреляция, лишенная данных недостатков (см. рис. 3).

Согласно рисунку 3 сильная корреляция (больше 0,6) со значениями целевых переменных наблюдается у следующих признаков: HTL, Cs, MA, FA, I, Br.

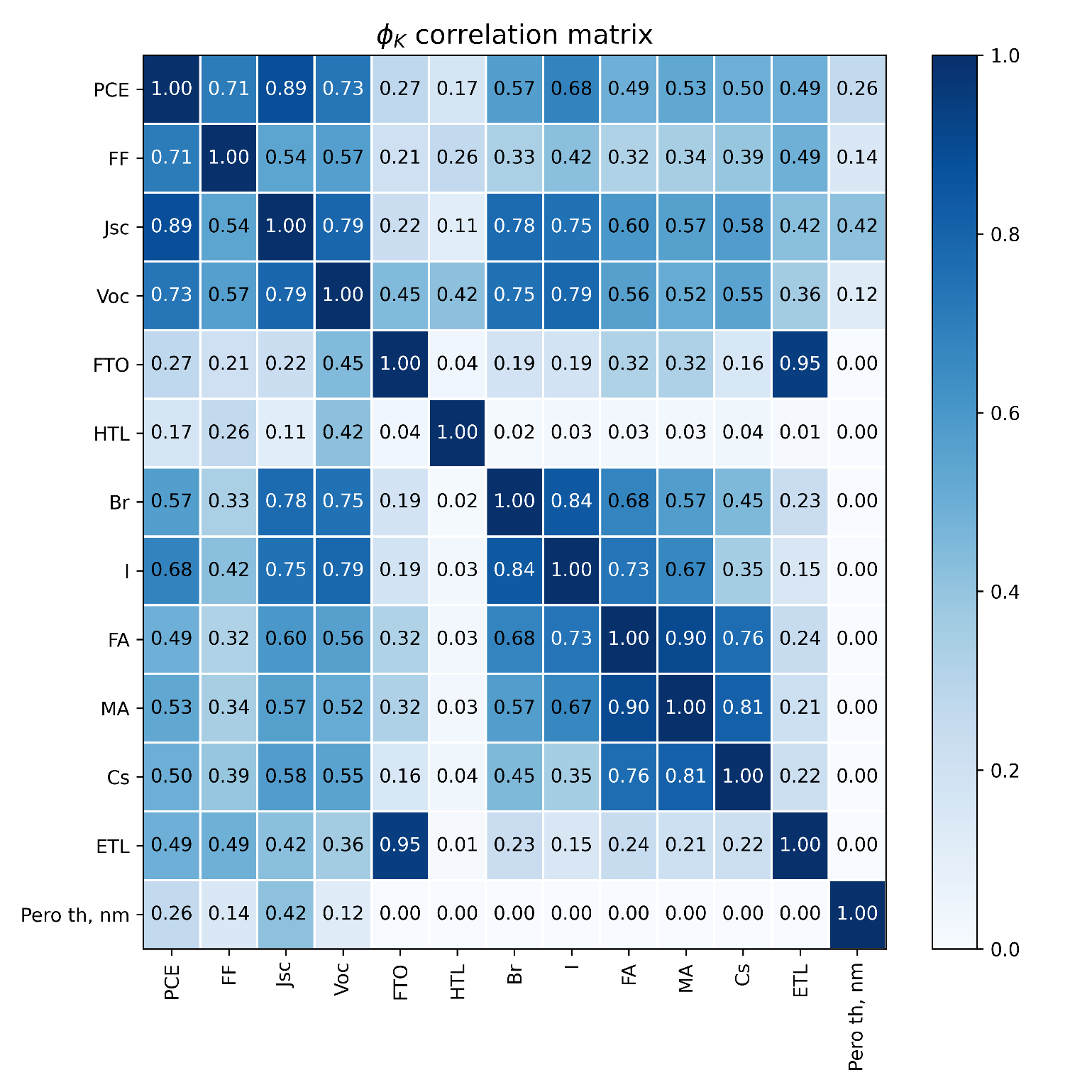
Рисунок 3 - Матрица коэффициентов корреляции φk

DOI:10.60797/IRJ.2024.143.121.4

Однако при оценке корреляций необходимо также исследовать статистическую значимость данной корреляции.

Для определения значимости, необходимо учесть значение p-критерия. Значение p менее 0,05 обычно считается статистически значимым, и в этом случае нулевую гипотезу следует отклонить на взятом уровне значимости, то есть связь между двумя наблюдаемыми событиями существует. Значение p больше 0,05 означает, что нулевая гипотеза не отвергается, следовательно, не существует связи между двумя наблюдаемыми событиями.

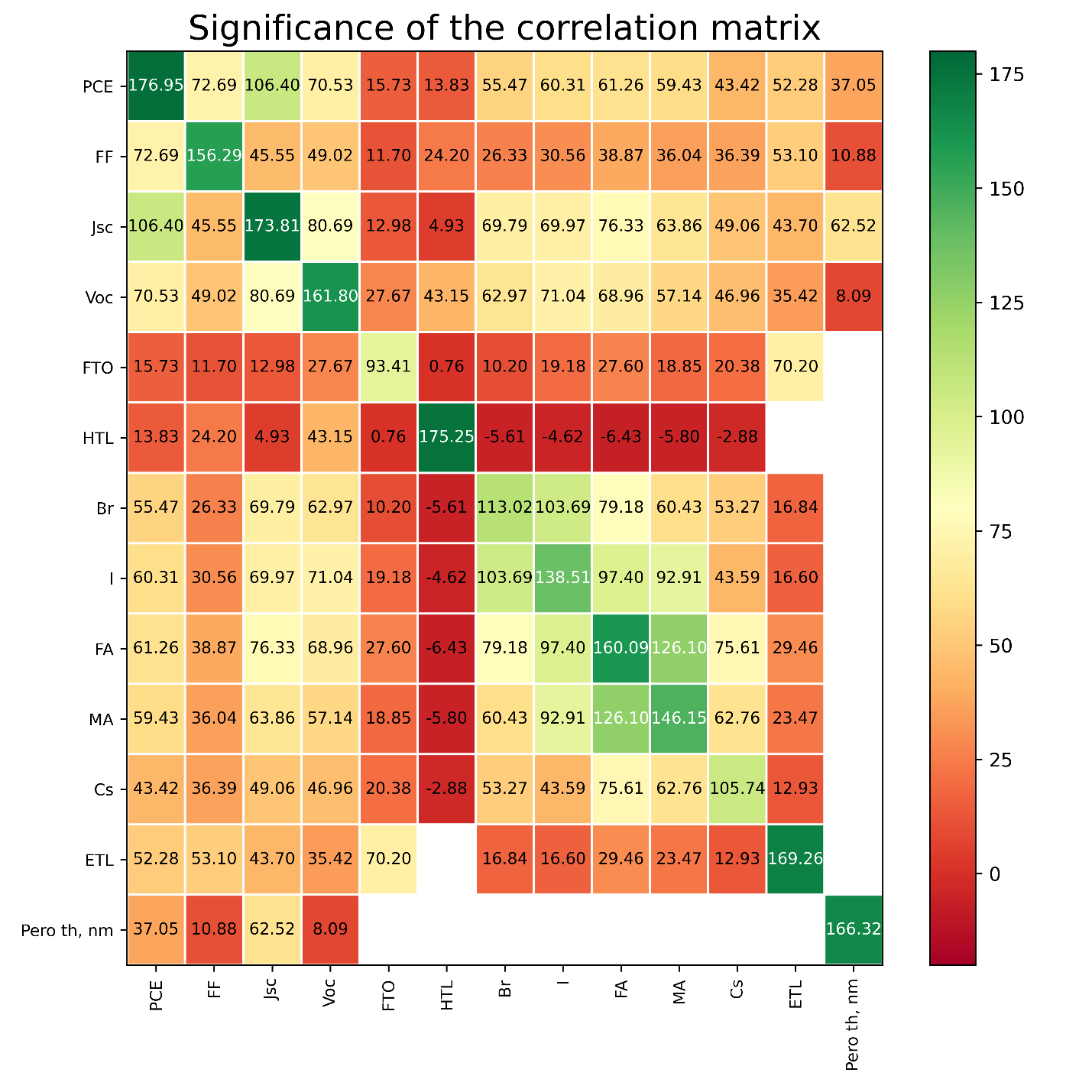
Рисунок 4 - Значимость корреляции

DOI:10.60797/IRJ.2024.143.121.5

Согласно рисунку 4 почти все коэффициенты корреляции признаков (кроме ‘Pero th, nm’, ‘HTL’, ‘FTO’, ‘Cs’, ‘ETL’) с целевыми переменными статистически значимы при выбранном уровне значимости. Также стоит отметить, что в матрице отсутствуют некоторые значения коэффициентов значимости корреляции, поскольку нет зависимости между данными переменными.

В качестве алгоритмов машинного обучения применялись не только базовые алгоритмы, такие как линейная регрессия (англ. Linear Regression), К-ближайших соседей (англ. K-Nearest Neighbors), метод опорных векторов (англ. Support vector Machine), дерево решений (англ. Decision Tree), но и современные ансамблевые методы, такие как случайный лес (англ. Random Forest) и методы основанные на бустинге (англ. Extreme Gradient Boosting (XGBoosting), Light Gradient Boosting Machine (LightGBM), Gradient Boosting Regressor). Для тонкой настройки алгоритмов, а также для борьбы с переобучением необходимо использовать разбиение набора данных на обучающую и тестовую выборки, кросс-валидацию, различные регуляризации, масштабирование признаков, подбор гиперпараметров при помощи метода GridSearchCV и другие приемы для увеличения обобщающей способности алгоритмов. В результате на основе выбранных алгоритмов можно будет оценить важность выбранных признаков, а также оценить точность алгоритмов по метрикам средняя квадратичная ошибка (англ. mean squared error, MSE) и средняя абсолютная ошибка (англ. mean absolute error, MAE).

Далее представлены результаты обучения алгоритмов, а также важности признаков для первого этапа.

Исходя из данных таблицы 2, низкую ошибку показали ансамблевые методы (Random Forest и методы, основанные на бустинге).

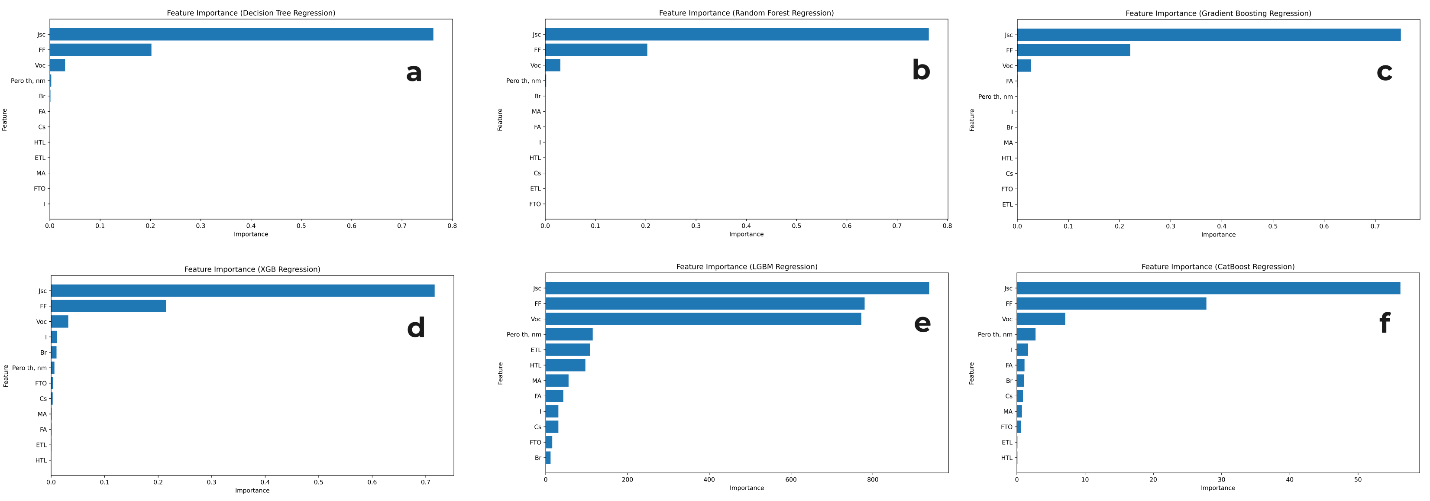
Рисунок 5 - Важность признаков в алгоритмах

Примечание: Примечание: a – decision tree regression, b – random forest regression, c – gradient boosting regression, d – xgboosting regression, e – lightgbm regression, f – catboost regression

DOI:10.60797/IRJ.2024.143.121.7

Почти все алгоритмы показали примерно одинаковые значения важности признаков (см. рис. 5). Из рисунков видно, что наибольшую важность вносят следующие признаки: 'Voc', 'Jsc', 'FF'. Методы, основанные на бустинге LightGBM и CatBoost показали, что помимо вышеупомянутых признаков, также важны, но в меньшей степени, такие признаки как 'Pero th', 'ETL', 'Cs', 'MA', 'FA', 'I', 'HTL'.

Далее представлены результаты обучения алгоритмов для второго этапа.

Исходя из данных табл. 3, самые низкие значения ошибки показали следующие алгоритмы: XGBoosting, CatBoost и Random Forest.

В работе были применены методы машинного обучения для поиска наилучших параметров PSC с высоким PCE. Для обучения алгоритмов был создан набор данных, содержащий информацию о PSC, таких как толщина перовскитного слоя, тип электронно-транспортного слоя и т.д., а также целевые переменные: Voc, Jsc, FF и PCE. Были применены различные алгоритмы машинного обучения, включая линейную регрессию, K-ближайших соседей, метод опорных векторов, дерево решений, случайный лес и методы, основанные на бустинге. Результаты показали, что:

1) низкую ошибку на обоих этапах обучения показали XGBoosting, CatBoost и Random Forest;

2) наибольшую важность для PCE имеют такие параметры, как Voc, Jsc и FF;

3) дополнительными важными параметрами, в меньшей степени влияющими на PCE, являются Pero th, ETL, Cs, MA, FA, I и HTL.

Данная работа демонстрирует потенциал применения машинного обучения для оптимизации PSC и может быть использована для ускорения разработки новых материалов с высокой PCE.