IMPROVING THE DURABILITY OF PLAIN BEARER WITH NONLINEAR SHAPE AND METAL COVERING
ТЕХНИЧЕСКИЕ НАУКИ / ENGINEERING
DOI: https://doi.org/10.2 3670/IRJ.2022.119.5.043
ПОВЫШЕНИЕ ИЗНОСОСТОЙКОСТИ ПОДШИПНИКА СКОЛЬЖЕНИЯ С НЕЛИНЕЙНЫМ КОНТУРОМ И МЕТАЛЛИЧЕСКИМ ПОКРЫТИЕМ
Научная статья
ORCID: 0000-0002-0737-1846,
Ростовский государственный университет путей сообщения, Ростов-на-Дону, Россия
* Корреспондирующий автор (bolgova_katya6[at]mail.ru)
Аннотация
В работе представлена методика формирования точного решения задачи гидродинамического расчета трибосистемы с нестандартным, адаптированным к условиям трения опорным профилем ползуна и направляющей с металлическим покрытием. На основе использования уравнений: движения несжимаемой жидкости для «тонкого слоя» с учетом сил инерции; уравнении неразрывности и уравнении, определяющего профиль расплавленного контура поверхности направляющей с металлическим покрытием, учитывая скорость механической энергии, получены аналитические зависимости для основных рабочих характеристик пары трения для экстремального и не экстремального случая.
Ключевые слова: гидродинамика, опора скольжения, расплавленная поверхность направляющей, адаптированный профиль, экстремальный случай.
IMPROVING THE DURABILITY OF PLAIN BEARER WITH NONLINEAR SHAPE AND METAL COVERING
Research article
Bolgova E.A.*
ORCID: 0000-0002-0737-1846,
Rostov State Transport University, Rostov-on-Don, Russia
* Corresponding author (bolgova_katya6[at]mail.ru)
Abstract
The work presents an adequate hydrokinetic calculation method of tribosystem with slide surface support profile and metal covered runner, adjusted to friction. Based on the following equations: ideal liquid movement for "thin layer", inertial force accounted for; continuity, metal covered runner surface fused shape profile, mechanical energy accounted for, - analytical dependence of basic working characteristics for friction pair for extreme and non-extreme cases was drawn out.
Keywords: fluid dynamicist, sliding support, runner fused surface, adjusted profile, extreme case.
Введение
Общеизвестно, что работоспособность машин и механизмов в значительной степени зависит от конструкции узлов. Для обеспечения устойчивого гидродинамического режима смазывания в условиях смазочного голодания, особенно при пуске и выбегах, а также в случаях перекосов валов, можно обеспечить использованием новых моделей течения применяемых смазочных материалов с нестандартным опорным профилем подшипниковой втулки и металлическим или пористым покрытием рабочей поверхности. В современном машиностроении в качестве модели жидкого смазочного материала в опорах скольжения широко используются смазочные материалы, обладающие ньютоновскими и неньютоновскими реологическими свойствами, [1], [2], [12]. [13] а также смазочные материалы, обусловленные расплавом покрытия рабочих поверхностей. В приведенных расчетных моделях [14], [15], [23], [24] не учитывается влияние нелинейных факторов, кроме того рассматриваемые подшипники имеют традиционно линейный контур опорной поверхности. Разработанная расчётная модель подшипников скольжения, учитывающая нелинейные факторы и наличие расплава на одной из рабочих поверхностей, является одним из перспективных направлений современной трибологии. Данная статья посвящена исследованию выше изложенных особенностей, что является на наш взгляд актуальным.
Постановка задачи
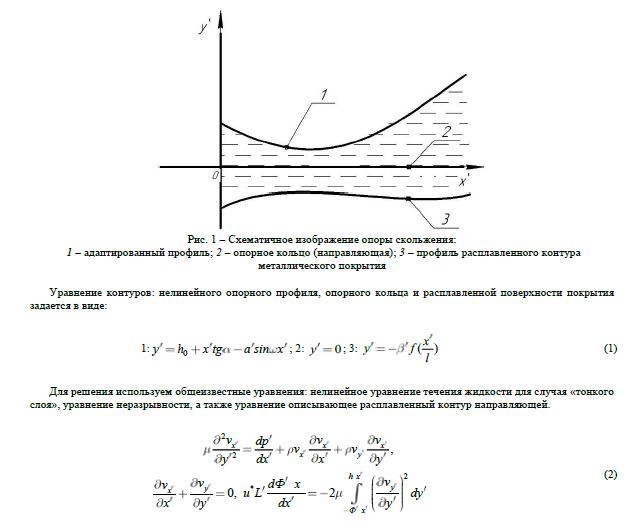
Рассмотрим установившиеся течение несжимаемой жидкости в рабочем зазоре нелинейной опоры скольжения. Предполагается, что нестандартная поверхность неподвижна, а опорное кольцо с металлическим покрытием движется со скоростью (рис.1).
В не экстремальном случае, то есть при промежуточных значениях L для определения контура расплавленной поверхности, направляющей воспользуемся третьим уравнением системы (2), предварительно осредним интегрально по промежутку Ф(x),h(x) . Для нахождения функции характеризующей контур расплавленного покрытия получаем следующее уравнение:
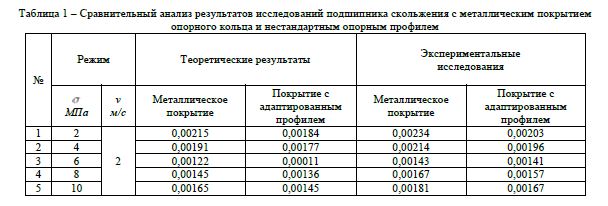
Анализ полученных результатов подтверждает эффективность теоретических моделей и доказывает преимущества исследованных подшипников, обеспечивающих повышение несущей способности и снижение коэффициента трения. По результатам экспериментального исследования полученный гидродинамический режим характеризуется после приработки (колебания) коэффициент трения 0,0011 – 0,00215 независимо от условия нагружения. При этом величина износа не превысила 0,0095мм.
Анализ полученных результатов подтверждает эффективность теоретических моделей и доказывает преимущества исследованных подшипников, обеспечивающих повышение несущей способности и снижение коэффициента трения.
По результатам экспериментального исследования полученный гидродинамический режим характеризуется после приработки (колебания) коэффициент трения 0,0011 – 0,00215 независимо от условия нагружения. При этом величина износа не превысила 0,0095мм.

| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Mukutadze M. A. Working out of an analytical model of an axial bearing taking into account dependence of viscous characteristics of micropolar lubrication on pressure and temperature / A. Mukutadze, E. O. Lagunova, K. S. Solop //International Journal of Applied Engineering Research. – 2017. – № 14. – Vol. 12.– pp. 4644-4650.
- Расчетная модель радиального подшипника скольжения с повышенной несущей способностью, работающего на микрополярной смазке с учетом ее вязкостных характеристик от давления /К. С. Ахвердиев, М. А. Мукутадзе, Е. О. Лагунова и др. // Инженерный вестник Дона. – 2013. – №4 (27). – С. 22.
- Расчетная модель упорного подшипника скольжения с повышенной несущей способностью, работающего на неньютоновских смазочных материалах с адаптированной опорной поверхностью / К. С. Ахвердиев, М. А. Мукутадзе, Е. О. Лагунова и др. // Инженерный вестник Дона. – 2013. – №4 (27). – С. 23.
- Расчетная модель гидродинамической смазки неоднородного пористого подшипника конечной длины, работающего в устойчивом нестационарном режиме трения при наличии принудительной подачи смазки / М. А. Мукутадзе, Б. М. Флек, Н. С. Задорожная и др. // Инженерный вестник Дона. – – №3 (26). – С. 9.
- Akhverdiev K. S. Hydrodynamic calculation of a thrust plain bearing that operates with viscoelastic lubricant under turbulent friction conditions/ K. S. Akhverdiev, M. A. Mukutadze, I. S.Semenko // Journal of Machinery Manufacture and Reliability. – 2011. – № 4. – Vol. 40. – pp. 359-365.
- Стратифицированное течение трехслойной смазки в зазоре упорного подшипника, обладающего повышенной несущей способностью / К. С. О. Ахвердиев, А. Ч. Эркенов, Е. Е. Александрова и др. // В сборнике: Трибология и надежность.Сбор.научн. трудов X Международной конференции. Федеральное агентство ж.-д. трансп., ФГБОУ ВПО "Петербургский государственный университет путей сообщения Императора Александра I", Межведомственный науч. совет по трибологии при РАН, Российский нац. ком. по трибологии; под общ. ред. К.Н. Войнова. – Санкт-Петербург, 2010. – С. 15-24.
- Стратифицированное течение двухслойной смазки в зазоре упорного подшипника, обладающего повышенной несущей способностью / К. С. Ахвердиев, Е. В. Александрова, Е. Е. Кручинина и др. // Вестник Донского государственного технического университета. – 2010. – №2 (45). – Т. 10. – С. 217-223.
- Гидродинамический расчет радиального подшипника скольжения, работающего в турбулентном режиме трения при неполном заполнении зазора вязкоупругой смазкой / К. С. О. Ахвердиев, М. А. Мукутадзе, В. А. Замшин и др. //Вестник машиностроения. – 2009. – № – С. 11-17.
- Ахвердиев К.С. Гидродинамический расчет радиального подшипника при наличии электромагнитного поля с учетом зависимости вязкости и электропроводимости от температуры /К. С. Ахвердиев, Е. О. Лагунова, М. А. Мукутадзе //Вестник Донского государственного технического университета. – 2009. – № 3 (42). – Т. 9.– С. 529-536.
- Математическая модель гидродинамической смазки бесконечно широких опор, работающих в турбулентном режиме на микрополярной смазке /К. С. Ахвердиев, А. Ю. Вовк, М. А. Мукутадзе и др. // Трение и смазка в машинах и механизмах. 2007. – № – С. 12-15.
- Мукутадзе М. А.Разработка системы расчетных моделей подшипников скольжения на основе развития гидродинамической и реодинамической теории смазки. Автореферат дис. доктора технических наук / РГУПС. Ростов-на-Дону, 2015.
- Гидродинамический расчет радиального подшипника, работающего в нестационарном режиме на вязкопластичной смазке, обладающей микрополярными свойствами /К. С. Ахвердиев, М. А. Мукутадзе, А. Ю. Вовк и др. //Вестник Ростовского государственного университета путей сообщения. – 2008. – №4 (32). – С. 131-138.
- Математическая модель гидродинамической смазки радиального подшипника, работающего в нестационарном режиме на микрополярной смазке /К. С. Ахвердиев, М. А. Мукутадзе, М. А. Савенкова и др. //Вестник Ростовского государственного университета путей сообщения. – 2008. – №1 (29). – С. 147-15.
- Мукутадзе М. А. Гидродинамическая модель клиновидной опоры скольжения с легкоплавким металлическим покрытием / М. А. Мукутадзе, Д. У. Хасьянова, А. М.Мукутадзе // Проблемы машиностроения и надежности машин. – 2020. – № – С. 51-58.
- Mathematical model of a plain bearer lubricated with molten metal / A. Mukutadze, V. V. Vasilenko, A.M. Mukutadze et al. //В сборнике: IOP Conference Series: Earth and Environmental Science. International Conference on Innovations and Prospects of Development of Mining Machinery and Electrical Engineering. – 2019. – С. 012021.
- Mukutadze M. A. Simulation model of thrust bearing with a free-melting and porous coating of guide and slide surfaces / A. Mukutadze, A. M. Mukutadze, V. V.Vasilenko // В сборнике: IOP Conference Series: Materials Science and Engineering. – Novosibirsk, 2019. – pp. 012031.
- Mukutadze M.A. Radial friction bearing with a fusible coating in the turbulent friction mode / A. Mukutadze, D. U. Khasyanova // Journal of Machinery Manufacture and Reliability. – 2019. – VOL. 48. – № 5. – PP. 421-430.
- Akhverdiev K. S. Calculated model of wedge-shaped sliding supports taking into account rheological properties of viscoelastic lubricant / S. Akhverdiev, E. O. Lagunova, M. A.Mukutadze // Advances in Engineering Research. Proceedings of the International Conference "Aviamechanical engineering and transport" (AVENT 2018). – 2018. – PP. 246-253.
- Mukutadze M. A. Optimization of the supporting surface of a slider bearing according to the load-carrying capacity taking into account the lubricant viscosity depending on pressure and temperature / A. Mukutadze, D. U. Khasyanova // Journal of Machinery Manufacture and Reliability. – 2018. – VOL. 47. – № 4. – PP. 356-361.
- Mukutadze M. A., Development of the design model of a hydrodynamic lubricating material formed during melting of the axial bearing, in the presence of forced lubrication / A. Mukutadze, E. O. Lagunova, V. V. Vasilenko //Journal of Machinery Manufacture and Reliability. – 2018. – VOL. 47. – № 3. – PP. 271-277.
- Mathematical model of a radial sliding bearing with a porous layer on its operating surface with a low-melting metal coating on shaft surface / S. Akhverdiev, E. A. Bolgova, M. A. Mukutadze et al. // IOP Conference Series: Materials Science and Engineering. Сер. "International Conference on Mechanical Engineering, Automation and Control Systems, MEACS 2020". – 2021. – PP. 012005
- Кохановский В. А. Матричные материалы антифрикционных композитов /В. А. Кохановский, М. А.Мукутадзе // Вестник Донского государственного технического университета. 2001. – Т. 1. – № – С. 51-56.
- Lagunova E. O. Calculation of a radial slider bearing with a fusible coating / O. Lagunova, M. A.Mukutadze // Journal of Friction and Wear. – 2019. – Т. 40. – № 1. – С. 88-94.
- Mukutadze M. A. Optimization of the supporting surface of a slider bearing according to the load-carrying capacity taking into account the lubricant viscosity depending on pressure and temperature / A. Mukutadze, D. U. Khasyanova //Journal of Machinery Manufacture and Reliability. – 2018. – Т. 47. – № 4. – С. 356-361.
Список литературы на английском языке / References in English
- Mukutadze M. A. Working out of an analytical model of an axial bearing taking into account dependence of viscous characteristics of micropolar lubrication on pressure and temperature / A. Mukutadze, E. O. Lagunova, K. S. Solop //International Journal of Applied Engineering Research. – 2017. – Vol. 12. – № 14. – PP. 4644-4650.
- Raschetnaja model' radial'nogo podshipnika skol'zhenija s povyshennoj nesushhej sposobnost'ju, rabotajushhego na mikropoljarnoj smazke s uchetom ee vjazkostnyh harakteristik ot davlenija. [Calculation model of a radial sliding bearing with increased bearing capacity, operating on a micropolar lubricant, taking into account its viscosity characteristics from pressure] / K. S. Akhverdiev, M. A. Mukutadze, E. O. Lagunova et al. // Inzhenernyj vestnik Dona. [Engineering vestnik of the Don]. – 2013. – No. 4 (27). – p. 22. [in Russian]
- Raschetnaja model' upornogo podshipnika skol'zhenija s povyshennoj nesushhej sposobnost'ju, rabotajushhego na nen'jutonovskih smazochnyh materialah s adaptirovannoj opornoj poverhnost'ju [Calculation model of a thrust sliding bearing with increased bearing capacity, operating on non-Newtonian lubricants with an adapted bearing surface] / K. S. Akhverdiev, M. A. Mukutadze, E. O. Lagunova et al. // Inzhenernyj vestnik Dona [Engineering vestnik of the Don]. – 2013. – No. 4 (27). – p. 23. [in Russian]
- Raschetnaja model' gidrodinamicheskoj smazki neodnorodnogo poristogo podshipnika konechnoj dliny, rabotajushhego v ustojchivom nestacionarnom rezhime trenija pri nalichii prinuditel'noj podachi smazki [Computational model of hydrodynamic lubrication of a nonuniform porous bearing of finite length operating in a stable non-stationary friction mode in the presence of forced lubrication supply] / M. A. Mukutadze, B. M. Fleck, N. S. Zadorozhnaya et al. // Inzhenernyj vestnik Dona [Engineering vestnik of the Don]. – 2013. – No. 3 (26). – p. 9.[in Russian]
- Akhverdiev K. S. Hydrodynamic calculation of a thrust plain bearing that operates with viscoelastic lubricant under turbulent friction conditions / S. Akhverdiev, M. A. Mukutadze, I. S. Semenko // Journal of Machinery Manufacture and Reliability. – 2011. – Vol. 40. – № 4. – PP. 359-365.
- Stratificirovannoe techenie trehslojnoj smazki v zazore upornogo podshipnika, obladajushhego povyshennoj nesushhej sposobnost'ju [Stratified flow of a three-layer lubricant in the gap of a thrust bearing with increased bearing capacity] / K. S. O. Akhverdiev, A. Ch. Erkenov, E. E. Alexandrova et al. // In the collection: Tribology and reliability. Collection of scientific papers of the X International Conference. Federal Agency of Railway Transport, St. Petersburg State University of Railways of Emperor Alexander I, Interdepartmental Scientific. Council on Tribology at the Russian Academy of Sciences, Russian National Com. on tribology; under the general editorship of K.N. Voynov. – Saint Petersburg, 2010. – pp. 15-24. [in Russian]
- Stratificirovannoe techenie dvuhslojnoj smazki v zazore upornogo podshipnika, obladajushhego povyshennoj nesushhej sposobnost'ju [Stratified flow of a two-layer lubricant in the gap of a thrust bearing with increased bearing capacity] / K. S. Akhverdiev, E. V. Alexandrova, E. E. Kruchinina et al. // Vestnik Donskogo gosudarstvennogo tehnicheskogo universiteta [Vestnik of the Don State Technical University]. – 2010. – Vol. 10. – No. 2 (45). – pp. 217-223. [in Russian]
- Gidrodinamicheskij raschet radial'nogo podshipnika skol'zhenija, rabotajushhego v turbulentnom rezhime trenija pri nepolnom zapolnenii zazora vjazkouprugoj smazkoj [Hydrodynamic calculation of a radial sliding bearing operating in a turbulent friction mode with incomplete filling of the gap with viscoelastic lubricant] / K. S. O. Akhverdiev, M. A. Mukutadze, V. A. Zamshin et al. // Vestnik of Mechanical Engineering. – 2009. – No. 7. – pp. 11-17. [in Russian]
- Akhverdiev K. S. Gidrodinamicheskij raschet radial'nogo podshipnika pri nalichii jelektromagnitnogo polja s uchetom zavisimosti vjazkosti i jelektroprovodimosti ot temperatury [Hydrodynamic calculation of a radial bearing in the presence of an electromagnetic field taking into account the dependence of viscosity and electrical conductivity on temperature] / K. S. Akhverdiev, E. O. Lagunova, M. A.Mukutadze // Vestnik Donskogo gosudarstvennogo tehnicheskogo universiteta [Vestnik of the Don State Technical University]. – 2009. – Vol. 9. – No. 3 (42). – pp. 529-53. [in Russian]
- Matematicheskaja model' gidrodinamicheskoj smazki beskonechno shirokih opor, rabotajushhih v turbulentnom rezhime na mikropoljarnoj smazke [Mathematical model of hydrodynamic lubrication of infinitely wide supports operating in turbulent mode on micropolar lubrication] / K. S. Akhverdiev, A. Yu. Vovk, M. A. Mukutadze et al. // Friction and lubrication in machines and mechanisms. – 2007. – No. 9. – pp. 12-15. [in Russian]
- Mukutadze M. A. Razrabotka sistemy raschetnyh modelej podshipnikov skol'zhenija na osnove razvitija gidrodinamicheskoj i reodinamicheskoj teorii smazki [Development of a system of calculation models of sliding bearings based on the development of the hydrodynamic and rheodynamic theory of lubrication] M. A. Mukutadze abstract dis.Doctors of Technical Sciences /Rostov-on-Don, 2015. [in Russian]
- Gidrodinamicheskij raschet radial'nogo podshipnika, rabotajushhego v nestacionarnom rezhime na vjazkoplastichnoj smazke, obladajushhej mikropoljarnymi svojstvami [Hydrodynamic calculation of a radial bearing operating in a non-stationary mode on a viscoplastic lubricant with micropolar properties] K. S. Akhverdiev, M. A. Mukutadze, A. Yu. Vovk et al. // Vestnik Rostovskogo gosudarstvennogo universiteta putej soobshhenija. [Vestnik of the Rostov State Transport University]. – 2008. – No. 4 (32). – pp. 131-138. [in Russian]
- Matematicheskaja model gidrodinamicheskoj smazki radial'nogo podshipnika, rabotajushhego v nestacionarnom rezhime na mikropoljarnoj smazke [Mathematical model of hydrodynamic lubrication of a radial bearing operating in non-stationary mode on micropolar lubrication] / K. S. Akhverdiev, M. A. Mukutadze, M. A. Savenkova et al. // Vestnik Rostovskogo gosudarstvennogo universiteta putej soobshhenija. [Vestnik of the Rostov State Transport University]. – 2008. – No. 1 (29). – pp. 147-15. [in Russian]
- Mukutadze M. A. Gidrodinamicheskaja model' klinovidnoj opory skol'zhenija s legkoplavkim metallicheskim pokrytiem [Hydrodynamic model of a wedge-shaped sliding support with a fusible metal coating] / M. A. Mukutadze, D. U. Khasyanova, A. M. Mukutadze // Problems of mechanical engineering and machine reliability. – 2020. – No. 4. – pp. 51-58.[in Russian]
- Mathematical model of a plain bearer lubricated with molten metal / A. Mukutadze, V. V. Vasilenko, A. M. Mukutadze et al. // IOP Conference Series: Earth and Environmental Science. International Conference on Innovations and Prospects of Development of Mining Machinery and Electrical Engineering 2019. – 2019. – pp. 012021.
- Mukutadze M. A. Simulation model of thrust bearing with a free-melting and porous coating of guide and slide surfaces / A. Mukutadze, A. M. Mukutadze, V. V.Vasilenko // IOP Conference Series: Materials Science and Engineering. – Novosibirsk, 2019. – C. 012031.
- Mukutadze M. A. Radial friction bearing with a fusible coating in the turbulent friction mode / A. Mukutadze, D. U. Khasyanova // Journal of Machinery Manufacture and Reliability. – 2019. – Vol. 48. – № 5. – Pp. 421-430.
- Akhverdiev K. S. Calculated model of wedge-shaped sliding supports taking into account rheological properties of viscoelastic lubricant / S. Akhverdiev, E. O. Lagunova, M. A.Mukutadze // Advances in Engineering Research. Proceedings of the International Conference "Aviamechanical engineering and transport" (AVENT 2018). – 2018. – PP. 246-253.
- Mukutadze M. A. Optimization of the supporting surface of a slider bearing according to the load-carrying capacity taking into account the lubricant viscosity depending on pressure and temperature / A. Mukutadze, D. U.Khasyanova // Journal of Machinery Manufacture and Reliability. – 2018. – Vol. 47. – № 4. – PP. 356-361.
- Mukutadze M. A., Development of the design model of a hydrodynamic lubricating material formed during melting of the axial bearing, in the presence of forced lubrication / A. Mukutadze, E. O. Lagunova, V. V. Vasilenko // Journal of Machinery Manufacture and Reliability. – 2018. – Vol. 47. – № 3. – PP. 271-277.
- Mathematical model of a radial sliding bearing with a porous layer on its operating surface with a low-melting metal coating on shaft surface / S. Akhverdiev, E. A. Bolgova, M. A. Mukutadze et al. // IOP Conference Series: Materials Science and Engineering. Сер. "International Conference on Mechanical Engineering, Automation and Control Systems, MEACS 2020". – 2021. – PP. 012005
- Kohanovsky V. A. Matrichnye materialy antifrikcionnyh kompozitov [Matrix materials of antifriction composite] / V. A. Kohanovsky, M. A. Mukutadze // Vestnik of the Don State Technical University. – 2001. – Vol. 1. – No. 2. – pp. 51-56.[in Russian]
- Lagunova E. O. Calculation of a radial slider bearing with a fusible coating / O. Lagunova, M. A.Mukutadze // Journal of Friction and Wear. – 2019. – Vol. 40. – № 1. – pp. 88-94.
- Mukutadze M. A. Optimization of the supporting surface of a slider bearing according to the load-carrying capacity taking into account the lubricant viscosity depending on pressure and temperature / A. Mukutadze, D. U. Khasyanova // Journal of Machinery Manufacture and Reliability. – 2018. – Vol. 47. – № 4. – pp. 356-361