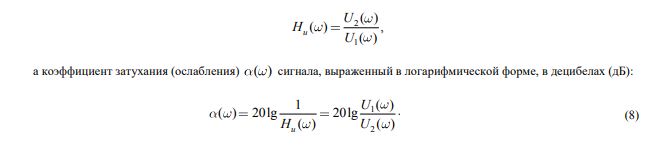THE USE OF EDUCATIONAL AND SOFTWARE ENVIRONMENTS IN STUDY OF DISCIPLINE «ELECTRICAL ENGINEERING AND ELECTRONICS» DURING THE COVID-19 PANDEMIC

DOI:https://doi.org/10.23670/IRJ.2022.119.5.053

ИСПОЛЬЗОВАНИЕ УЧЕБНО-ПРОГРАММНЫХ СРЕД ПРИ ИЗУЧЕНИИ ДИСЦИПЛИНЫ «ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА» В УСЛОВИЯХ ПАНДЕМИИ COVID-19

Научная статья

Марченко А.Л.^*

ORCID: 0000-0002-1825-0023,

Московский авиационный институт, Москва, Россия

^* Корреспондирующий автор (marchenkoal[at]mail.ru)

Аннотация

Вынужденный перевод технических вузов полностью или частично в связи с вирусной пандемией на дистанционную форму обучение студентов потребовал разработки и использования электронных образовательных ресурсов для поддержки всех видов аудиторных занятий и самостоятельной работы студентов при изучении технических дисциплин, в том числе дисциплины «Электротехника и электроника». Курс указанной дисциплины требует большой практической работы при ограниченном объеме выделенных часов на изучение курса. Использование разработанных электронных образовательных ресурсов (учебно-программных сред моделирования и анализа электронных устройств, учебно-программных тренажеров, компьютерного лабораторного практикума и др.) позволило выполнить требования ФГОС ВО последнего поколения по обеспечению качества подготовки студентов по дисциплине. В статье приведен пример использования учебно-программной среды ARCF при изучении активного RC-фильтра, благодаря которой появилась возможность снизить вероятность появления вычислительных ошибок, свести к минимуму рутинную счетную работу для построения графиков частотных характеристик фильтра и тем самым к увеличению времени на решение поставленных задач обучения.

Ключевые слова: учебно-программная среда, электроника, активный RC-фильтр.

THE USE OF EDUCATIONAL AND SOFTWARE ENVIRONMENTS IN STUDY OF DISCIPLINE «ELECTRICAL ENGINEERING AND ELECTRONICS» DURING THE COVID-19 PANDEMIC

Research article

Marchenko A.L. ^*

ORCID: 0000-0002-1825-0023,

Moscow Aviation Institute, Moscow, Russia

^* Correspondent author (marchenkoal[at]mail.ru)

Abstract

The forced transfer of technical universities, altogether or partly, due to the pandemic, to distance learning required the development and use of electronic educational resources to support all types of classroom studies and work of students in their study of technical disciplines, including the discipline of «Electrical engineering and electronics». Its course requires a lot of practical work with a limited amount of hours allocated for the studying. Use of developed electronic educational resources (educational and software environments of modeling and analysis of electronic devices, educational and training software, computer laboratory workshop, etc.) made it possible to meet the requirements of the FSES HE last edition of quality assurance of students' training in the discipline. The article provides an example of the educational and software environment of ARCF use in the study of the active RC-filter, with which it became possible to reduce the probability of  computational errors occurrences, to minimize the routine counting work for constructing charts of frequency characteristics of the filter and this way to increase the time to solve the set tasks of training.

Keywords: educational and software environment, electronics, active RC-filter.

Введение

Концепция дистанционного образования предполагает наличие или разработку учебно-программных сред (УПС) моделирования и анализа электронных устройств, учебно-программных тренажеров, компьютерного лабораторного практикума, сессий тестирования с мультимедийными заданиями в открытой форме и др.), необходимых для успешного формирования у обучаемых профессиональных компетенций в изучаемой предметной области, предписанных в ФГОС ВО последнего поколения [1].

Использование кафедральных лицензионных УПС типа Mathcad, Multisim и др. для моделирования и анализа электронных устройств при дистанционном образовании невозможно, так как они функционируют только при их инсталляции на конкретном вычислительном устройстве (ВУ) обучаемого, поэтому для поддержки учебного процесса по электротехническим дисциплинам дря всех видов занятий используются открытые или разработанные на кафедрах УПС.

Содержание типового УПС обычно включает обобщенную схему электронного устройства, техническое задание на проектирование на ее основе вариантов заданий, рекомендованную методику его синтеза, пример расчета параметров элементов схемы с построением графиков характеристик смоделированного устройства. Составленный отчет о выполненных заданиях студенты отправляют для контроля в lms-структуру вуза.

Учебно-программные тренажеры [2], [3], [4], [5], разработанные с участием студентов в рамках их проектной деятельности, функционируют в двух режимах: в тренировочном и контрольном. При работе в тренировочном режиме оцениваются действия студента при выполнении каждого этапа задания: при его программной проверке отмечаются красным цветом ошибочные операции и выводятся подсказки по их устранению. Он может многократно выполнять этот этап задания без ограничения времени, до устранения ошибок, так как для него заблокирован переход к выполнению следующего этапа задания.

В контрольном режиме студент выполняет задание в течение ограниченного времени без подсказок с выводом интегральной оценки за выполнение всех операций задания в баллах, вычисленных как отношение правильно выполненных операций к общему числу необходимых действий.

Учебно-программные среды и тренажеры включены в учебно-методические комплексы: по электротехнике [6], [7] и электронике [8], [9].

Моделирование, расчет и построение характеристик ARC-фильтров

Рассмотрим одну из подобных учебно-программных сред - среду АRCF, разработанную с использованием программной среды BorlandC++ Builder. Для функционирования среды ARCF необходимо ВУ с ОС Windows 11, c браузером MSEdge и объемом свободной памяти 20 МБ.

Цель разработки УПС АRCF- создание электронного образовательного ресурса по изучению методики синтеза активных RC-фильтров студентами технических вузов всех форм обучения для поддержки учебного процесса модуля «Электроника» как в условиях вспышек пандемии, так и при сокращении объема аудиторных часов на треть и более в последние годы по многим направлениям подготовки бакалавров с увеличения времени на самостоятельную работу на изучение дисциплины «Электротехника и электроника»

Задача проектирования активных RC-фильтров представляет собой типовую задачу синтеза, которая решается математическим методом, при котором процедура проектирования состоит из ряда последовательно выполняемых этапов. При этом результаты, полученные в процессе решения задач на предыдущем этапе, являются исходными данными для задач, решаемых на последующих этапах проектирования.

Основными этапами проектирования активных RC-фильтров являются: а) формулировка и решение аппроксимационной задачи: обычно используется идеализированная нормированная амплитудно-частотная характеристика Нu(w); б) выбор элементной базы и схемная реализация ARC-фильтра нижних частот.

Основные теоретические положения

Требования к миниатюризации электронной аппаратуры фильтрации сигналов на низких частотах (скажем, с частотами среза wс = 10…500 Гц) привели к разработке активных фильтров, которые не содержат индуктивных элементов и могут быть реализованы в виде интегральных микросхем.

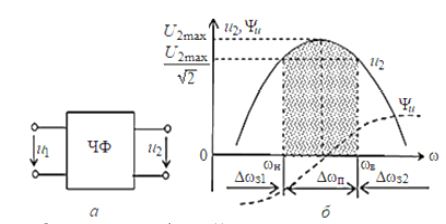
Частотный (полосно-пропускающий) фильтр (ЧФ) - селективный четырёхполюсник (рис. 1, а), пропускающий без заметного ослабления электрические колебания (напряжения, тока) определённых частот и подавляющий колебания остальных частот. Полосу частот с возможно малым затуханием, например, напряжения u2 называют полосой пропускания Δωп (рис. 1, б), а полосы частот с большим ослаблением сигнала - полосами задерживания (задержки) Δωз1 и Δωз2. Граничные частоты между полосой пропускания и полосами задерживания называют частотами среза wс: нижней wн и верхней wв. Тогда ширина полосы пропускания Δωп = wв -wн.

Рис. 1 - Условное обозначение частотного фильтра (а), граничные частоты и полосы пропускания и задержки напряжения u2 полосового фильтра (б)

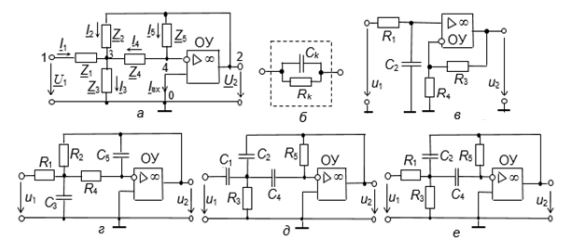
Активные RC-фильтры (ARC-фильтры) состоят из активных элементов (транзисторов, операционных усилителей и др.), работающих в линейном режиме, постоянных резисторов R и конденсаторов С (RC- двухполюсников). На рис. 2 даны примеры реализации звена 2-го порядка АRC-фильтра в общем виде (а), состоящего из операционного усилителя ОУ и пяти RC-двухполюсников Zk (б), звена 1-го порядка (в) и звеньев 2-го порядка фильтров нижних (ФНЧ) (г) и верхних (ФВЧ) (д) частот и полосового фильтра (ПФ) (е) [12].

Рис. 2 – Схемы звеньев ARC-фильтров

Определение коэффициентов передачи звеньев ARC-фильтров

В качестве объекта моделирования электронного устройства был выбран активный RC-фильтр, построенный на основе операционных усилителей (ОУ) с бесконечным усилением и с многопетлевой отрицательной обратной связью.

Существует много способов реализации АRС-фильтра с заданной передаточной функцией по напряжению Нu(р) п-го порядка. Наиболее распространенным является способ, при котором эту функцию представляют в виде произведения сомножителей (звеньев) второго порядка [11], т.е.

а для фильтров нечетного порядка в качестве сомножителя входит функция одного звена 1-го порядка.

Заменив оператор р = jw в передаточной функции Hu(p) звена, получают его комплексный коэффициент передачи Hu(jw) = U2/U1, а после несложных преобразований функции Hu(jw) - его амплитудно-частотную Hu(w) (АЧХ) и фазо-частотную Y(w) (ФЧХ) (см. рис. 1, б) характеристики.

Используя обобщенную схему звена (см. рис. 2, а) АRC-фильтра, найдем выражение его коэффициента передачи по напряжению Hu(w). Для этого составим уравнения первого закона Кирхгофа для узлов 3 и 4 схемы с учетом того, что входной ток ОУ Iвх » 0 и напряжение U4 » 0 [10]:

где Yk = 1/Zk = 1/Rk + jwCk = gk + jwCk- комплексная пров одимость k-го вухполюсника в предположении, что каждый двухполюсник содержит параллельно включенные резистор Rk и конденсатор Ck (см. рис. 2, б).

Используя выражения (2) и (3), соответствующим выбором параметров двухполюсников, в которых оставляют один элемент (либо резистор, либо конденсатор), получают выражения коэффициентов передачи Hk(jw) звеньев разных типов фильтров.

Примечание. На базе одного ОУ, в обратной связи которого отсутствуют звенья типа Т-образного моста, рекурсивный фильтр реализовать нельзя [12].

Базовой моделью при математическом описании передаточной функции п-го порядка ARC-фильтров является фи­льтр ФНЧ. Фильтры с другими частотными характеристиками – ФВЧ и ПФ – рассматривают как модификации базовой модели.

Так, для звена 2-го порядка ФНЧ (см. рис. 2, г) комплексный коэффициент передачи Hu(jw) по напряжению

где с0, b и с - нормированные коэффициенты; H0 - коэффициент усиления звена при w = 0; wс = 2pfс - угловая частота среза зве­на фильтра.

В таблице 1 приведены коэффициенты bk и сk для фильтров ФНЧ типов В и Т от 2-го до 6-го порядков включительно, заимствованные из таблиц справочника [12], где они приведены с бόльшим числом значащих цифр и для существенно бόльшего числа разновидностей фильтров.

Таблица 1 - Варианты задания

n ®	2		3		4			5					6
Звено	1		1	2	1	2		1	2		3		1	2		3
amaх ¯	Нормированные к wс = 1 рад/c коэффициенты функции Нu(р) звеньев ARC-фильтров типов В и Т
Тип B: -3,0 дБ при wс	b c	1,4142 1,0000	-1,0000	1,0000 1,0000	0,7654 1,0000		1,8478 1,0000	-1,0000		0,6180 1,0000		1,6180 1,0000	0,5176 1,0000		1,4142 1,0000	1,9319 1,0000
Тип T: -0,1 дБ	b с	2,3124 3,3140	-0,9694	0,9696 1,6891	0,5283 1,3300		1,2755 0,6229	-0,5389		0,3331 1,1949		0,8719 0,6359	0,2294 1,1294		0,6267 0,6964	0,8561 0,2634
Тип T: -0,5 дБ	b c	1,4256 1,5162	-0,6265	0,6265 1,1424	0,3507 1,0635		0,8467 0,3564	-0,3623		0,2239 1,0358		0,5862 0,4768	0,1553 1,0230		0,4243 0,5900	0,5794 0,1570
Тип Т: -1,0 дБ	b с	1,0977 1,1025	-0,4942	0,4042 0,9942	0,2791 0,9865		0,6737 02794	-0,2895		0,1789 0,9883		0,4684 04293	0,1244 0,9907		0,3398 0,5577	0,4641 0,1247
Тип Т: -2,0 дБ	b с	0,8038 0,8231	-0,3689	0,9942 1,6897	02098 0,9287		0,5064 0,2216	-0,2183		01349 0,0522		0,3592 0,3932	0,0939 0,9660		,02367 0,5329	0,3506 0,0999
Tип Т: -3,0 дБ	b с	0,6440 0,7079	-0,2986	0,9694 1,6897	0,1703 0,9031		0,4112 0,1960	-01795		0,3331 1,1949		0,8719 0,6359	0,0765 0,9548		0,2089 0,5216	0,2853 0,0888

Примечание: коэффициент усиления звеньев Н0 = 2, частота среза фильтра fс = 100 Гц, amin = -40 или -50 дБ

Введение в выражение (6) угловой частоты среза wс даёт возможность оперировать безразмерными коэффициентами bk и сk: они нормированы приведением к частоте wс = 1 рад/с для не­равномерности коэффициента передачи Hu(w) в полосе про­пускания, рассчитанной: для фильтров Баттерворта так, что на частоте среза wс их АЧХ имеют спад -3 дБ , а АЧХ фильтров Чебышева типа T на частоте wс имеют спад, равный значению допустимых пульсаций в полосе пропускания, т.е. в полосе пропускания АЧХ пульсирует между уровнем  и 1, где обычно принимается amax = -0,1, -0,5, -1,0, -2,0 или -3,0 дБ. Так, например, при amax = -0,5 дБ АЧХ пульсирует между уровнями 0,944 и 1.

При больших значениях H0 и Q чрезвычайно расширяется диапазон параметров элементов схемы и требуются более сложные схемы звеньев.

В теории фильтров за основной параметр принимают не АЧХ фильтра

В полосе пропускания Dwп идеальных фильтров коэффициент затухания и  т.е. затухания нет. В реальных фильтрах достичь значения  в полосе Dwп невозможно даже при полном согласо­вании фильтра с источником сигнала и нагрузкой на какой-то частоте, так как входные характеристические сопротивления фильтров зависят от частоты.

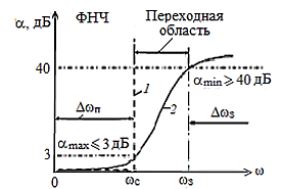
В качестве примера на рис. 3 представлена характеристика затухания  идеального (кривая 1) и реального (кривая 2) фильтра нижних частот.

Рис. 3 – График логарифмической АЧХ идеального 1 и реального 2 ФНЧ

Минимальное гарантированное значение коэффициента затухания  на границе полосы задерживания (на частоте , см. рис. 3) обычно принимают равным , иногда

Расчет параметров элементов звеньев и ARC-фильтра ФНЧ

Исходными данными для расчета ФНЧ являются:

• wс - частота среза фильтра;
• допустимое небольшое затухание amax [дБ] в полосе пропускания Dwп;
• wз - граничная частота задерживания;
• относительно большое затуха­ние amin [дБ] на границе частоты wз;
• метод аппроксимации идеального АЧХ фильтра (фильтр Баттерворта или фильтр Чебышева);
• H0 – коэффициент усиления при w = 0;
• n – порядок фильтра.

Примечание. Обычно порядок п фильтра находят по формулам или номограммам, приводимым в справочниках [11], [12], используя заданные коэффициенты amax, amin и частоты wс и wз: чем меньше |amax| и больше |amin|, тем ýже переходная область (wз -wс) и выше порядок п фильтра.

Выписываем из таблицы 1 коэффициенты: с0 полинома 1-го порядка при нечетном п; bk и сk полиномов 2-го порядка вида .

Выражения для расчета параме­тров Rk и Ck двухполюсников (см. рис. 2, г), получим путём почленного сопоставления выражений табличного Hu(р) звена с полученной функцией Hu(р) звена. Один из параметров звена (обычно С3) выбирают произвольно (в долях микрофарад) или близкое к значению C3 » 10/fс [мкФ], где циклическая частота fс фильтра в герцах.

Итак, сопоставляя формулы (5) и (6), нетрудно вывести формулы для расчёта сопротивлений резисторов и ёмкостей конденсаторов звеньев 1-го и 2-го порядков. Так, для ФНЧ В и T типов 2-го порядка из сопоставления указанных формул

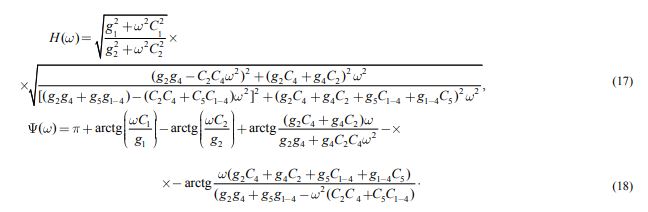
Выполнив умножение АЧХ звеньев (17) и сложив их ФЧХ (18), получим выражения АЧХ и ФЧХ фильтра, а взяв 20lg[H(w)] от АЧХ звеньев и фильтра, а также lgw- выражения логарифмических частотных характеристик (ЛАЧХ и ЛФЧХ) звеньев и фильтра.

Моделирование фильтра ARC-ФНЧ-Т5 в среде ARCF

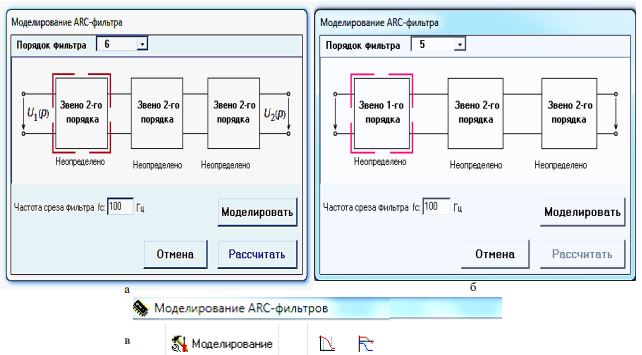
Моделирование заданного типа ARC-фильтра выполним на основе обобщенной его схемы, состоящей из трёх звеньев, представленных в виде квадратов (рис. 4, а).

При вводе в активное окно модели трехзвенного ARC-фильтра значения его порядка n = 3 или n = 5 первое звено 2-го порядка автоматически преобразовывается в звено 1-го порядка (рис. 4, б).

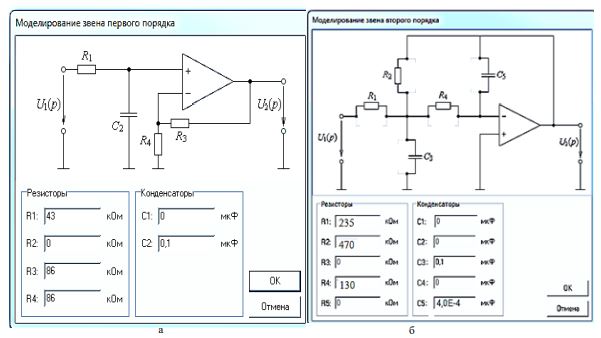
После ввода порядка фильтра n = 5, частоты среза fc = 100 Гц (см. рис. 4, б) и щелчка мышью на кнопке с надписью Моделировать, на экран ВУ выводится схема звена 1-го порядка (рис. 5, а) с активными полями, в которые нужно ввести с клавиатуры ВУ найденные значения параметров элементов его схемы, завершая ввод щелчком мышью на кнопке ОК. При этом всплывает модель схемы фильтра (см. рис. 4, б).

Рис. 4 – Стартовые станицы среды ARCF моделирования ARC-фильтров:

Рис. 5 – Моделирование звеньев:

 1-го (а) и 2-го (б) порядков фильтра АRC-ФНЧ-Т5

После щелчков мышью на втором квадрате модели фильтра и на кнопке Моделировать, ввод параметров первого звена 2-го порядка производится на выведенной на экран схеме (рис. 5, б): вначале «убирается» изображение резистора Rk или конденсатора Ck из каждого двухполюсника звена после щелчков мышью на их изображениях. При этом автоматически обнуляются значения их параметров, которые были записаны в размещенные ниже схемы активные поля.

После ввода в активные поля найденных ранее значений параметров для оставшихся в этом звене элементов схемы и щелчка мышью на кнопке ОК выводится вновь заставка с обобщенной моделью фильтра (см. рис. 4, б). Щелкнув мышью на третьем квадрате и на кнопке Моделировать, и выполнив описанные выше операции по моделированию оставшегося второго звена 2-го порядка, нужно щелкнуть мышью на кнопке ОК, а затем на ставшей активной кнопке Рассчитать (см. рис. 4, б, внизу справа).

Расчет по программам среды ARCF: АЧХ, ФЧХ, ЛАЧХ и ЛФЧХ как отдельных звеньев, так и фильтра в целом, ведется с формированием базы данных указанных функций. По окончании расчетов вверху рабочего поля среды ARCF активируются две кнопки (рис. 4, в): кнопка  и кнопка .

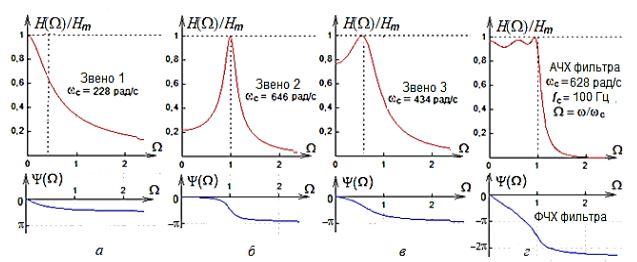
Щелчком мыши на кнопке  на экран ВУ выводятся графики нормированных АЧХ çH(W)/Hmçи ФЧХ Y(W) отдельных зве­ньев и трехзвенного фильтра (рис. 6), где Hm- максимальное значение функции Hu(W);

Рис. 6 – Нормированные АЧХ и ФЧХ звеньев (а, б и в) и фильтра АRC-ФНЧ-Т5 (г)

Анализ результатов моделирования ARC-фильтра свидетельствует, что вид графиков и значения основных параметров характеристик звеньев и трехзвенного АRС-фильтра с допустимыми отклонениями соответствуют их виду и рассчитанным значениям параметров.

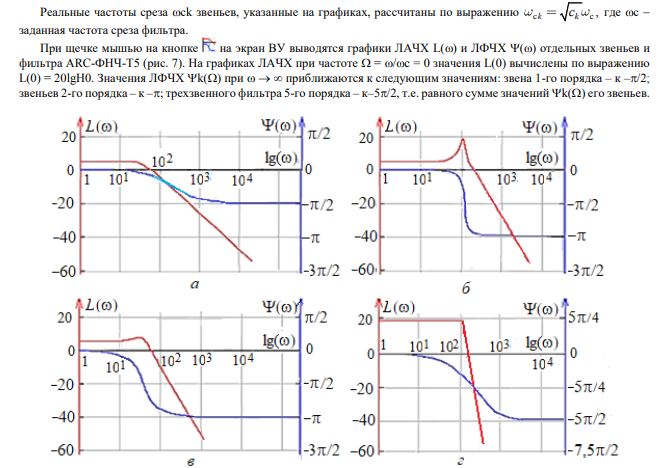
Реальные частоты среза wсk звеньев, указанные на графиках, рассчитаны по выражению  где wс - заданная частота среза фильтра.

Рис. 7 – ЛАЧХ и ЛФЧХ звеньев (а, б и в) и фильтра АRC-ФНЧ-Т5 (г)

Моделирование АRC-фильтра в программной среде NIMultisim

Исследуем возможность применимости программной среды NIMultisim при решении поставленной задачи, и проверим вероятность появления вычислительных ошибок в разработанной среде ARCF.

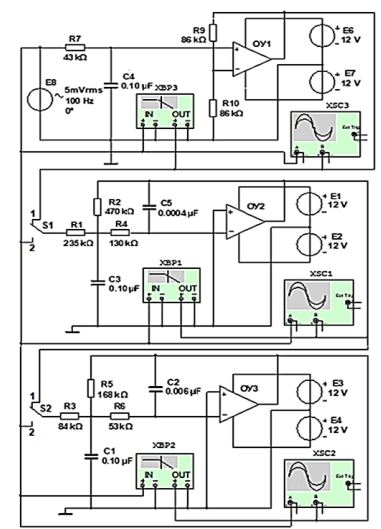
Электрическая схема (рис. 8) собрана из звеньев активного ФНЧ Чебышева 5-­го порядка (ARC-ФНЧ-Т5) на рабочем поле программной среды моделирования и анализа схем электронных устройств NIMultisimv.11 (в дальнейшем -MS11), с введенными значениями параметров элементов обобщенной схемы активного RC-фильтра

Для отображения графической информации (аналогичных графиков частотных характеристик, представленных на рис. 6 и рис. 7), во все схемы звеньев вставлены модели плоттеров XBP1-XBP3 среды MS11, а для снятия осциллограмм входного и выходного напряжений u1 и u2 каждого звена - модели двухканальных осциллографов XSC1-XSC3.

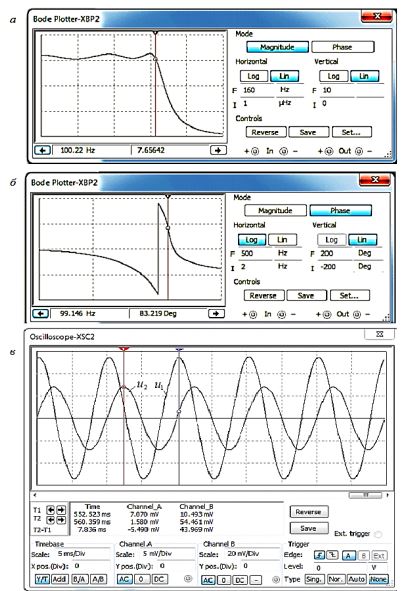
При испытании звена 1-го порядка и фильтра ARC-ФНЧ-Т5 переключатели S1 и S2 должны быть в положениях 1, первого звена 2-го порядка – переключатель S1 нужно включить в положения 2, а при испытании второго звена 2-го порядка – S1 вернуть в положении 1, а S2 включить в положении 2 (см. рис. 8). После щелчков мышью на изображениях плоттеров XSC1-XSC3, осциллографов XSC1-XSC3 и на кнопке запуска среды MS11, на их экранах (рис. 9) устанавливались пределы изме­нения частоты f, угла сдвига фаз Yu(f) (Phase), коэффициента передачи Нu(f)

(Magnitude), выбирались логарифмические (Log) или линейные (Lin) шкалына осях графиков АЧХ и ФЧХ звеньев, а также визирные линии на частотах звена 3:  и

Рис. 8 -Электрическая схема фильтра ARС-ФНЧ-Т5

Рис. 9 – АЧХ (а) и ФЧХ (б) и осциллограммы напряжений u1 и u2 фильтра ARC-ФНЧ-Т5 (в)

часть графика опустить вниз (к началу скачка вверх), то легко убедиться, что при увеличении частоты f отставание выходного напряжения u2 от входного u1 стремится к -450 (см. график ФЧХ () на рис. 7, г (среда ARCF)).

Заключение

Показана возможность моделирования по известной методике параметров элементов схемы частотного активного RC-фильтра, и вывода на экран ВУ графиков частотных характеристик звеньев и многозвенного фильтра, рассчитанных посредством программного обеспечения, содержащегося в учебно-программной среде ARCF.

Сравнение частотных характеристик ФНЧ Чебышева 5-го порядка, полученных при моделировании в среде ARCF (см. рис. 7, г) и в среде МS11 (см. рис. 9, а и б), показало, что их изменения носят аналогичный характер, а значения характерных точек (Нс, wс звеньев и др.) на графиках АЧХ и ФЧХ отличаются незначительно от расчетных значений указанных величин. Это свидетельствует о малой вероятности появления вычислительных ошибок при выполнении вариантов заданий по моделированию и построению частотных характеристик активных RC-фильтров в среде ARCF.

Благодаря использованию учебно-программной среды ARCF появилась возможность свести к минимум рутинную счетную работу для построения графиков частотных характеристик фильтра и тем самым к увеличению времени на решение поставленных задач обучения.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Марченко А. Л. Актуальные вопросы разработки и использования электронных изданий и ресурсов в обучении электротехнике и электронике в вузе. Монография. / А. Л.Марченко.- М.: ДМК Пресс. 2010. - 272 с.
2. Беневоленский С.Б. Использование виртуальных тренажеров в процессе изучения электротехнических дисциплин. / С.Б.Беневоленский, А.Л. Марченко.-M.: Педагогическая информатика. 2009. – №3. - С. 24-30.
3. Марченко А.Л. Программные комплексы для испытания электрических двигателей. / А.Л. Марченко.- М.: Вестник компьютерных и информационных технологий, 2011. – №11. - С. 30-35.
4. Марченко А.Л.Тренажер МИВ для анализа трехфазных цепей. Свидетельство о регистрации электронного ресурса в Институте научной информации и мониторинга РАО №17229 от 28.06.2011./ А.Л.Марченко, С.С.Воробьев, А.Г.Иванов
5. Марченко А.Л.Тренажер Э5 для анализа цифровых схем. Свидетельство о регистрации электронного ресурса в ОФЕРНиО №22131 от 06.09.2016 г. / А.Л.Марченко, Ю.Ф.Опадчий, Д.А.Шульгин
6. Марченко А.Л. Разработка учебно-методического комплекса по электротехнике. / А.Л. Марченко.- Екатеринбург: Международный научно-исследовательский журнал. Технические науки. – №10 (52). – Октябрь 2016, часть 2. -C. 86-92.
7. Марченко А.Л. УМК-Э1 (учебно-методический комплекс по электротехнике). Свидетельство о регистрации электронного ресурса в ОФЕРНиО №24117 от 24.06.2019 г.
8. Марченко А.Л. УМК-Э2 (учебно-методический комплекс по электронике). Свидетельство о регистрации электронного ресурса в ОФЕРНиО №24181 от 09.09.2019 г.
9. Марченко А.Л. Разработка учебно-методического комплекса по электронике: структура и функциональные возможности. / А. Л. Марченко // - Екатеринбург: Международный научно-исследовательский журнал. Технические науки. – №5 (95). – Май 2020, часть 1. -C. 49-58.
10. Марченко А.Л. Частотные фильтры: пассивные, активные и цифровые. Учебное методическое пособие. / А. Л. Марченко– М.: Горячая линия – Телеком. 2017. - 166 с.
11. Христиан Э. Таблицы и графики по расчёту фильтров. / Э.Христиан, Е.Эйзенман - М.: Связь. 1975. - 408 с.
12. Джонсон Д. Справочник по активным фильтрам. / Д.Джонсон, Дж.Джонсон, Г. Мур.- М.: Энергоатомиздат. 1983. - 218 с.

Список литературы на английском языке / ReferencesinEnglich

1. Маrchenko А.L. Aktual’niyevoprosyrazrabotkiiispol’zovaniyaelektronnykhizdaniyiresursovvobucheniielektrotekhnikeielektronikevvuze. Monografiya. [Topical issues of development and use of electronic publications and resources in teaching electrical engineering and electronics at the university. Monograph]. / А.L. Маrchenko.- М.: DMK Press. 2010. - P. 272. [in Russian]
2. Benevolenskiy S.B. Ispol’zovaniye virtual’nikh trenazhjorov v prozhese izucheniya elektrotekhnicheskikh disziplin [The use of virtual simulators in the process of studying electrical engineering diszhiplines]. / S.B.Benevolenskiy, А.L. Маrchenko - M.: Pedagogical Informatics. 2009, No. 3. - P. 24-30. [in Russian]
3. Маrchenko А.L. Programmnyye kompleksy dlya ispitaniya elektricheskykh dvigateley [Software systems for testing electric motors]. / А.L. Маrchenko .- M.: Vestnik computer and information technologii. 2011. No. 11. - P. 30-35. [in Russian]
4. Trenazher MIV dlja analiza triohfaznykh zhepey. Svidetel’stvo о registratsii elektronnogo resursa v Institute nauchnoy informatsii i monitoringa RAO [Simulator for the analysis of three-phase circuits. Certificate of registration of en electronic resource in Institute of scientific information and monitoring of the Russian Academy Education]. / А.L.Маrchenko, A.G.Ivanov, S.S. Vorobjov - No. 17229 оf 28.06.2011. [in Russian]
5. Маrchenko А.L.Trenazher E5 dlja analiza zhzifrovykh skhem. Svidetel’stvo о registratsii elektronnogo resursa v ОFЕRNiО [Simulator E5 for analysis of digital circuits. Certificate of registration of an electronic resource in OFERNiO]. / А.L.Маrchenko, U.F.Оpadchiy, D.A. Shulgin - No. 22131 оf 06.09.2016. [in Russian]
6. Маrchenko А.L. Razrabotka uchebno-metodicheskogo compleksa pо elektrotekhnike [Development of training materials in electrical engineering]. / А.L. Маrchenko .- Yekaterinburg: Mezhdunarodniy nauchno-issledovatel’skiy zhurnal. Tekhnicheskiye nauki [Yekaterinburg: International research journal. Technical sciences]. - No. 10 (52). - Oktober 2016. - Part 2. - P. 86-92. [in Russian]
7. Маrchenko А.L. UМК-E1 (uchebno-metodicheskiy compleks pо elektrotekhnike). Svidetel’stvo о registratsii elektronnogo resursa v ОFЕRNiО [UMC-E1 (educational and methodical complex on electrical engineering). Certificate of registration of an electronic resource in OFERNiO]. - No. 24117 оf 24.06.2019. [in Russian]
8. Маrchenko А.L. UМК-E2 (uchebno-metodicheskiy compleks pо elektronike). Svidetel’stvo о registratsii elektronnogo resursa v ОFЕRNiО [UMC-E2 (educational and methodical complex on electronics). Certificate of registration of an electronic resource in OFERNiO]. - No. 24181 оf 09.09.2019. [in Russian]
9. Маrchenko А.L. Razrabotka uchebno-metodicheskogo compleksa pо elektronike: struktura i funktsional’niye vozmozhnosti [Development of training on electronics: structure and functionality]. / А.L. Маrchenko .- Yekaterinburg: Mezhdunarodniy nauchno-issledovatel’skiy jurnal. Tekhnicheskiye nauki [Yekaterinburg: International research journal. Technical sciences]. - No. 5 (95). - May 2020. - Part 1. - P. 49-58. [in Russian]
10. Маrchenko А.L. Chastotnyye filtry: passivnyye, aktivnyye i tsifrovyye. Uchebnoye metodicheskoye posobiye [Frequency filters: passive, active and digital. Training manual]. / A.L. Marchenko .- M.: Hot line – Telekom. 2017. - 166 p. [in Russian]
11. Christian E. Tablitsy i grafiki po raschetu filtrov [Tables and graphs for the calculation of filters]. / E.Christian, E. Eisenman .- M.: Svyaz. 1975. - 408 p. [in Russian]
12. Dzhоnson D. Spravochnik po aktivnym filtram [Handbook of Active Filters]. / D.Johnson, J.Johnson, G. Moore.- M.: Energoatomizdat. 1983. - 218 p. [inRussian]