A SIMULATION OF A CONTROL LOOP FOR RADIO HOMING SYSTEMS VIA PROPORTIONAL NAVIGATION GUIDANCE

МОДЕЛИРОВАНИЕ КОНТУРА УПРАВЛЕНИЯ ДЛЯ РАДИОСИСТЕМ САМОНАВЕДЕНИЯ ПРИ НАВЕДЕНИИ МЕТОДОМ ПРОПОРЦИОНАЛЬНОЙ НАВИГАЦИИ

Научная статья

Буренко Е.А.*

ORCID: 0000-0003-0660-0843;

Московский авиационный институт (национальный исследовательский университет), Москва, Россия

* Корреспондирующий автор (super.evgeny-burenko2012[at]yandex.ru)

Аннотация

Разработана математическая модель контура управления для радиосистемы самонаведения крестокрылой управляемой ракеты класса «воздух-воздух» средней дальности при наведении на цель методом пропорциональной навигации (пропорционального наведения). Проведено математическое моделирование процессов наведения ракеты на воздушную цель, совершающую манёвр с заданной нормальной перегрузкой. В модели учтены угловые искажения, вносимые антенным обтекателем ракеты. Представлены результаты по оценке точности наведения ракеты с моноимпульсным суммарно-разностным пеленгатором, полученные на математической модели в результате статистического моделирования процессов наведения при действии флюктуаций углового шума воздушной цели. Представлены смоделированные траектории движения носителя, ракеты и цели в плоскости наведения, а также основные фазовые переменные модели, характеризующие процесс наведения.

Ключевые слова: радиосистема самонаведения, моноимпульсный пеленгатор, контур управления, метод пропорциональной навигации, математическое моделирование.

A SIMULATION OF A CONTROL LOOP FOR RADIO HOMING SYSTEMS VIA PROPORTIONAL NAVIGATION GUIDANCE

Research article

Burenko E.A.*

Moscow Aviation Institute (National Research University), Moscow, Russia

* Corresponding author (super.evgeny-burenko2012[at]yandex.ru)

Abstract

The current study develops a mathematical model of the control loop for the radio homing system of a medium-range cruciform-wing guided air-to-air missile when aiming at a target by the method of proportional navigation (proportional guidance). The author carries out a mathematical simulation of the processes of aiming a missile at an air target performing a maneuver with a given normal acceleration. The model takes into account the angular distortions introduced by the aerial fairing of the rocket. The article presents the results on the estimation of the accuracy of the missile guidance with a monopulse Sigma Delta direction finder obtained on a mathematical model as a result of statistical modeling of the guidance processes under the influence of fluctuations in the angular noise of the air target. The simulated trajectories of the carrier, missile, and target in the guidance plane are presented with the main phase variables of the model that characterize the guidance process.

Keywords: radio homing system, monopulse direction finder, control loop, proportional navigation method, mathematical modeling.

В настоящее время широкое развитие вычислительной и компьютерной техники позволяет производить математическое моделирование различных процессов в режиме реального времени. Целью настоящей статьи является разработка математической модели контура управления для радиосистемы самонаведения крестокрылой управляемой ракеты класса «воздух-воздух» средней дальности при наведении на цель методом пропорциональной навигации с визуальным отображением траекторий движения носителя, ракеты и цели в плоскости наведения.

Одним из наиболее мощных и эффективных средств моделирования различных систем и процессов является среда компьютерной алгебры MathCAD, в которой разработана модель контура управления. Для моделирования был использован математический аппарат дифференциальных уравнений и эквивалентный ему аппарат функциональных схем. Структура и блоки подробной математической модели контура управления, представленные своими дифференциальными уравнениями в правильной форме Коши, приводятся далее в основной части работы. Моделирование по оценке точности наведения ракеты проводилось при условии отсутствия помех и при воздействии на контур управления случайных флюктуаций углового шума цели.

Математическая модель контура управления

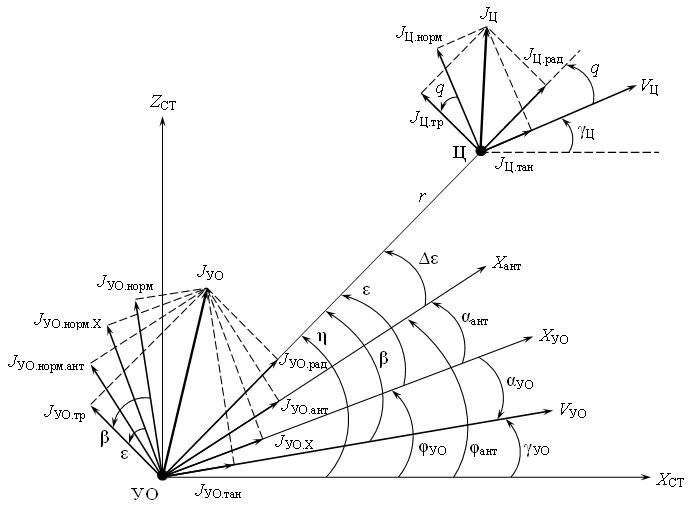
Рассматривается процесс самонаведения в стартовой системе координат OX_стZ_ст, невращающейся подвижной, в центре которой находится ракета, именуемая далее, как «управляемый объект» (УО). При этом рассматривается только один канал управления (канал курса) при движении в горизонтальной плоскости [1, С. 134], [2, С. 239]. Соответствующие геометрические соотношения представлены на рис. 1, где:

V_Ц – вектор скорости цели,

V_УО, X_УО – вектор скорости и строительная (продольная) ось управляемого объекта,

X_ант – ось антенны головки самонаведения управляемого объекта (соответствует равносигнальному направлению диаграммы направленности антенны), которая следит за целью,

r – линия визирования (вектор дальности, соединяющий управляемый объект и цель),

J_Ц – вектор ускорения цели,

Рис. 1 – Геометрические соотношения при самонаведении в стартовой системе координат

 

J_Ц.рад, J_Ц.тр – радиальная и трансверсальная составляющие вектора ускорения цели,

J_Ц.тан, J_Ц.норм – тангенциальная и нормальная составляющие вектора ускорения цели,

J_УО – вектор ускорения управляемого объекта,

J_УО.рад, J_УО.тр – радиальная и трансверсальная составляющие вектора ускорения управляемого объекта,

J_УО.X, J_УО.ант – проекции вектора ускорения управляемого объекта на его продольную ось X_УО и ось следящей антенны головки самонаведения (ГСН) X_ант,

J_УО.тан, J_{УО.норм} – тангенциальная и нормальная составляющие вектора ускорения управляемого объекта,

J_{УО.норм.X}, J_{УО.норм.ант} – составляющие вектора ускорения управляемого объекта, перпендикулярные (нормальные) его строительной оси X_УО и оси антенны ГСН X_ант,

γ_Ц, γ_УО – углы векторов скорости цели и управляемого объекта соответственно (курсовые углы цели и УО),

η – угол линии визирования, соединяющей управляемый объект и цель,

q = η – γ_Ц, β = η – γ_УО – углы между линией визирования r и векторами скоростей цели и управляемого объекта соответственно (углы упреждения цели и УО),

φ_УО, α_УО – углы поворота строительной оси (рысканья) и скольжения (атаки) соответственно управляемого объекта,

φ_ант, α_ант – углы поворота (рысканья) и разворота соответственно следящей антенны ГСН управляемого объекта,

ε – угол между продольной осью управляемого объекта X_УО и линией визирования r (угол пеленга цели),

∆ε – ошибка слежения по углу, которая определяется, как угол между направлением оси следящей антенны ГСН X_ант и направлением линии визирования цели r.

Направления отсчёта углов против часовой стрелки считаются положительными.

Модель контура управления создаётся с учётом:

- модели движения цели;

- модели движения ракеты;

- модели измерительного устройства;

- модели устройства формирования и передачи команд управления;

- модели относительного движения ракеты и цели.

В контуре управления все перечисленные модели образуют отдельные звенья.

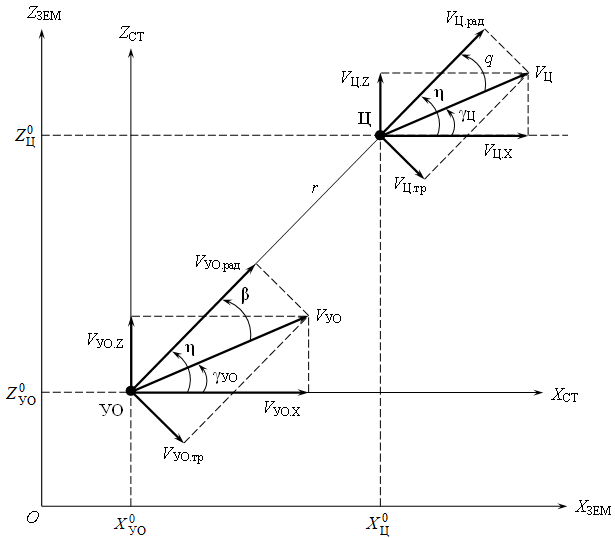
Модель относительного движения ракеты и цели (уравнения кинематической связи ракеты с целью) составляется исходя из проецирования векторов скоростей ракеты (управляемого объекта) и цели на линию визирования r и на нормаль к ней, что иллюстрируется рис. 2.

Рис. 2 – Формирование проекций векторов скоростей управляемого объекта и цели в плоскости наведения в земной системе координат

 

При этом образуются радиальные (V_УО.рад, V_Ц.рад) и трансверсальные (V_УО.тр, V_Ц.тр) составляющие векторов скоростей (радиальная составляющая направлена вдоль линии визирования, трансверсальная – по нормали к ней). Тогда модель относительного движения ракеты и цели представляется двумя дифференциальными уравнениями:

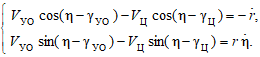     (1) Для решения уравнений численным методом, они должны быть представлены в правильной форме Коши: 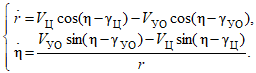     (2) В контуре управления полученные уравнения задают кинематическое звено. Начальные значения дальности r₀ от ракеты до цели и угла линии визирования η₀, соответствующие моменту времени отделения ракеты от носителя, определяются через начальные координаты ракеты   на момент отделения следующим образом (рис. 2):

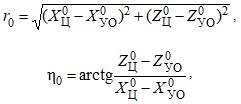
и задаются в виде соответствующих начальных условий системы (2).

В процессе наведения ракеты на цель имеют место ошибки наведения, вызванные различными факторами.

В частности, ошибки наведения, вызванные инерционностью контура управления при наличии манёвров цели, характеризуются соотношением:

    (3)

где h_max – максимальное значение ошибки (промаха), вызванной манёвром цели с ускорением J_Ц ≈ n_Ц·g (g = 9,81 м/с², n_Ц – перегрузка цели), при наличии в системе управления запаздывания на время τ_З. Из (3) следует, что данная ошибка вызвана совместным действием двух факторов – манёвра цели и запаздывания. При отсутствии любого из этих факторов ошибка данного вида исчезает. В предположении, что цель движется с максимальной перегрузкой n_Ц = 2 ед. п., а в системе управления имеет место временнóе запаздывание на τ_З ≈ 0,5 сек, то ошибка h_max в соответствии с (3) составляет приблизительно 1,635 м. Среднеквадратическое отклонение (СКО) ошибки (промаха) обусловленной манёвром цели характеризуется соотношением:

     (4)

и составляет приблизительно 0,545 м.

На точность наведения могут оказывать влияние угловые шумы (вызванные случайными флюктуациями направления прихода сигнала) и амплитудные шумы (вызванные флюктуациями амплитуды отражённого от цели сигнала). На моноимпульсные системы самонаведения амплитудные шумы практически не оказывают влияния, поскольку компенсируются в суммарно-разностном канале принимаемого сигнала.

Ошибки наведения могут вноситься также и антенным обтекателем, закрывающим антенну ГСН. При прохождении радиолуча через антенный обтекатель направление прихода сигнала изменяется на угол ν. Зависимость ошибки ν от угла прихода сигнала ε называется статической пеленгационной характеристикой ν(ε). Конкретный её вид зависит от вида поляризации сигнала, и поэтому даже при полной симметрии антенного обтекателя ошибки в разных плоскостях будут различными. Статическая пеленгационная характеристика очень трудно поддаётся расчёту и определяется экспериментальным путём. При моделировании систем самонаведения можно полагать, что функция ν(ε) задана. В модели контура управления функция ν(ε) аппроксимируется полиномом второй степени в виде:

    (5)

где ε – угол пеленга (в градусах),

ν – ошибка, вносимая обтекателем (в угловых минутах),

a₂ = –0,021, a₁ = –0,6, a₀ = 20,626 – коэффициенты полинома (5).

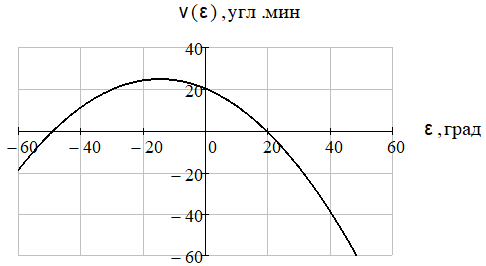
График функции (5) представлен на рис. 3.

 

Рис. 3 – Статическая пеленгационная характеристика антенного обтекателя ракеты, аппроксимированная полиномом второй степени

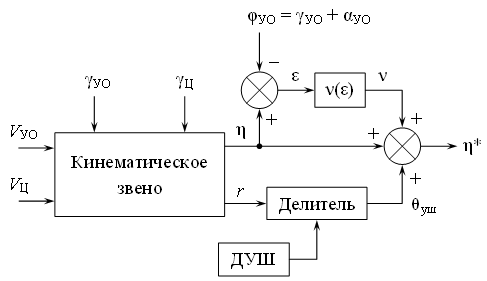
  Схема учёта ошибок, вносимых совместно антенным обтекателем и угловым шумом приведена на рис. 4.

Рис. 4 – Схема учёта ошибок, вносимых антенным обтекателем ракеты и угловым шумом цели

 

Здесь ДУШ – датчик углового шума, генерирующий шум со спектральной плотностью

    (6)

где k_УШ – коэффициент пропорциональности, который для разных типов целей может меняться в пределах k_УШ = 0,15 ÷ 0,33 град²/Гц [2, С. 263],

L_Ц – характерный размер цели.

Дисперсия величины промаха, обусловленная наличием углового шума цели, определяется как [2, С. 262]:

    (7)

где τ_УО ≈ 3,098 сек – аэродинамическая постоянная времени управляемого объекта (ракеты).

Для средней воздушной цели типа «истребитель» с эффективной площадью рассеяния (ЭПР) σ_Ц = 3 м², протяжённость составляет L_Ц ≈ 10 м, при этом дисперсия величины промаха в соответствии с (7) составляет  м², что соответствует СКО промаха σ₂ ≈ 2,541 м. Таким образом, СКО суммарной ошибки составляет

Данная ошибка учитывает только факторы, обусловленные характеристиками системы наведения, без учёта ошибок автопилота ракеты.

Конечной задачей наведения снаряда (ракеты) является поражение цели. В общем случае факт поражения рассматривается как случайное событие и оценивается некоторой условной вероятностью P_пор, определяемой как:

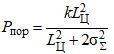    (8)

где L_Ц = 10 м – характерный размер цели,

k = 95% = 0,95 – эффективность заряда боевой части ракеты.

Таким образом, в соответствии с (8) оцениваемая вероятность поражения цели составляет приблизительно 0,837, что является достаточно высоким статистическим показателем моделируемой системы наведения.

Для решения задачи самонаведения используются различные методы наведения, определяющие закон движения ракеты. Наиболее распространённым методом наведения ракет «воздух-воздух» с радиолокационными системами самонаведения является метод пропорциональной навигации (пропорционального наведения). Данный метод применяется для наведения ракет на быстродвижущиеся и маневрирующие цели [2, С. 28-29].

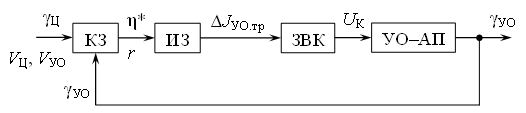
Структурная схема контура управления для метода пропорциональной навигации представлена на рис. 5.

Рис. 5 – Структурная схема контура радиоуправления для метода пропорциональной навигации

В состав контура входят:

КЗ – кинематическое звено, ИЗ – измерительное звено, ЗВК – звено выработки и передачи команд управления, УО–АП – звено «управляемый объект – автопилот» (ракета с автопилотом).

Сущность метода пропорциональной навигации состоит в том, что при движении ракеты задаётся оптимальное (требуемое) значение трансверсального ускорения ракеты  Закон управления вырабатывается через угловую скорость вращения линии визирования и имеет следующий вид:

    (9)

где N₀ = 3 – постоянная метода наведения (навигационная константа),

 – скорость сближения ракеты с целью (r – вектор дальности, соединяющий ракету и цель),

 – измеренная бортовой аппаратурой ракеты угловая скорость вращения линии визирования (η* – измеренный аппаратурой ракеты угол линии визирования),

Достоинством метода пропорциональной навигации является обеспечение малой перегрузки ракеты на протяжении всей траектории.

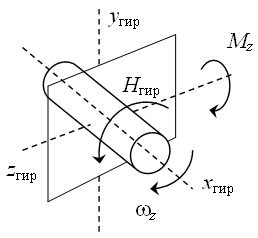
Для реализации метода используется специальный силовой следящий гиропривод на основе управляемого позиционного гироскопа. Гироскоп выполняет функции одновременно следящего и стабилизирующего устройств. Основное свойство позиционного гироскопа заключается в способности сохранять неизменным направление вращающегося ротора, ось которого является основной осью x_гир гироскопа, при колебаниях корпуса ракеты. В управляемом позиционном гироскопе имеется возможность создавать моменты M_y и M_z на осях y_гир и z_гир гироскопа, перпендикулярные его основной оси. Под действием этих моментов основная ось безынерционно поворачивается так, чтобы по кратчайшему пути совместить вектор кинетического момента гироскопа с моментами M_y и M_z (рис. 6). То есть, при действии момента M_z ось гироскопа вращается вокруг оси y_гир, а при действии момента M_y – вокруг оси z_гир. Данное явление называется прецессией. При этом проекции вектора угловой скорости разворота оси x_гир на плоскости, соответствующей контурам управления ракеты по курсу и тангажу, пропорциональны создаваемым моментам.

Рис. 6 – Прецессия гироскопа

 

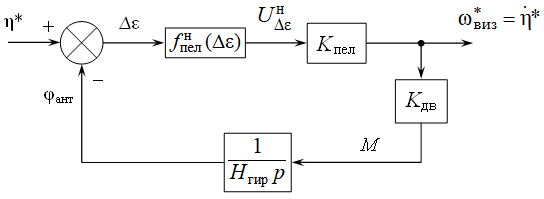
Совмещая подвижный элемент пеленгатора с ротором гироскопа, и используя его выходной сигнал для создания управляющих моментов M_y и M_z в каждом из контуров управления (по курсу и тангажу), образуется замкнутая следящая система с интегратором в цепи отрицательной обратной связи, соответствующая рис. 7.

Рис. 7 – Модель угломерного устройства ГСН с моноимпульсным пеленгатором и силовым следящим гироприводом

 

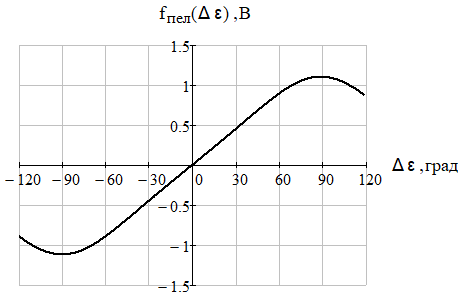
Пеленгатор в данном случае моделируется в виде последовательного соединения безынерционного нелинейного звена с нормированной пеленгационной характеристикой вида  и линейного динамического звена со статическим коэффициентом передачи K_пел. При этом крутизна пеленгационной характеристики в точке ∆ε = 0 совпадает с коэффициентом K_пел. Для моноимпульсного пеленгатора с суммарно-разностным методом измерения угловых координат пеленгационная характеристика имеет следующий вид [1, С. 5-6], [4, С. 382]:

   (10) где λ = 3 см – рабочая длина волны излучения ГСН, d = 0,8 см – расстояние между излучающими щелями антенны ГСН.  – нормированное напряжение на выходе пеленгатора. График пеленгационной характеристики (10) при заданных параметрах пеленгатора ГСН представлен на рис. 8.  

Рис. 8 – Нормированная пеленгационная характеристика моноимпульсного суммарно-разностного пеленгатора

 

При отклонении оси подвижного элемента пеленгатора (оси гироскопа x_гир) от направления цели на угол ∆ε пеленгатор вырабатывает сигнал рассогласования , который подаётся на моментный электродвигатель с коэффициентом передачи K_дв. Электродвигатель создаёт момент M, под действием которого ось x_гир, а вместе с ней и подвижный элемент пеленгатора поворачиваются в сторону цели с угловой скоростью , где H_гир – кинетический момент гироскопа, который определяется как , где J_x – момент инерции вращающегося тела гироскопа относительно оси x_гир, ω – угловая скорость вращения.

Система уравнений, описывающих устройство (рис. 7) имеет вид:

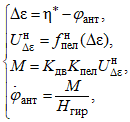
где .

Путём исключения промежуточных переменных в системе (11), образуется одно дифференциальное уравнение. Оно представлено в правильной форме Коши и имеет следующий вид:

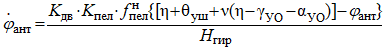    (12)

На выходе устройства (рис. 7) формируется измеренное значение угловой скорости вращения линии визирования, которое определяется как . В модели контура управления данное устройство является измерительным звеном.

Информационным признаком наведения в исследуемой системе является рассогласование реального (измеряемого) трансверсального ускорения с оптимальным (требуемым) (∆J_УО.тр). Тогда управляющая команда в звене выработки и передачи команд (ЗВК) вырабатывается в соответствии с выражением:

где f – функциональный оператор, определяющий правило формирования команды управления.

Звено выработки и передачи команд соответствует устройству формирования команд (формирователю команд), расположенному на ракете, и реализуемому обычно программно в бортовой электронно-вычислительной машине. Звено выработки команд представляется безынерционным звеном с коэффициентом передачи K_ЗВК, поэтому

   (13)

Реальное трансверсальное ускорение определяется датчиками линейных ускорений (ДЛУ), совмещёнными с осью антенны. Конструктивно ДЛУ могут быть установлены либо на подвижном элементе пеленгатора, либо непосредственно на корпусе ракеты. В первом случае ДЛУ будет формировать напряжение, пропорциональное составляющей ускорения J_{УО.норм.ант}, перпендикулярной оси X_ант следящего элемента пеленгатора. Поскольку направление оси X_ант отличается от направления линии визирования на ошибку слежения ∆ε, которая мала, то можно считать, что . Если подвижный элемент пеленгатора имеет малые массу и габариты, то установка на нём ДЛУ становится невозможной. В этом случае на корпусе ракеты размещаются два ДЛУ, измеряющие составляющие ускорения J_УО.X и J_{УО.норм.Х} (рис. 1). Для формирования напряжения, пропорционального трансверсальному ускорению, показания этих ДЛУ пересчитываются по формулам преобразования координат. Поскольку на борту ракеты направление линии визирования отождествляется с направлением оси X_ант, пересчёт даёт составляющую J_{УО.норм.ант}, которая близка к .

В обоих случаях для построения модели системы самонаведения модель ракеты должна формировать составляющую ускорения J_{УО.норм.ант}. Для этого вычисляется J_{УО.норм.ант} по формулам преобразования координат. С учётом того, что J_УО.тан  0, из геометрических соотношений (рис. 1) получается:

Нормальное скоростное ускорение (т. е. перпендикулярное вектору скорости ракеты) определяется из соотношения

Поскольку угол скольжения , то

где τ – аэродинамическая постоянная времени управляемого объекта.

Таким образом, реальное (измеряемое) трансверсальное ускорение управляемого объекта, пересчитанное в антенную систему координат, равно:

      (14)

В состав внешнего контура управления обязательно также входит звено «управляемый объект – автопилот». Входной переменной его является команда управления U_К, поступающая из ЗВК (13), а выходной – курсовой угол γ_УО, определяющий направление вектора скорости УО.

Модель управляемого объекта (крестокрылой осесимметричной ракеты) представляется системой дифференциальных уравнений, описывающих действие сил и моментов на ракету в процессе полёта:

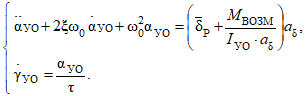Первое уравнение соответствует уравнению моментов, описывающему вращательное движение ракеты, второе уравнение – соответствует уравнению сил, описывающему динамику движения ракеты. Входной переменной модели (15) в общем случае является воздействие в виде суммы угла отклонения рулей  и внешнего возмущающего момента M_ВОЗМ, выходной переменной является угол вектора скорости управляемого объекта γ_УО.

В этих уравнениях:

a_δ – коэффициент при переменной воздействия в правой части уравнения,

I_УО – момент инерции управляемого объекта относительно осей OY_cв и OZ_св связанной системы координат,

ξ – коэффициент демпфирования (затухания), определяющий колебательные свойства управляемого объекта (определяет характер переходного процесса и зависит от конструктивных характеристик ракеты, скорости и высоты полёта),

ω₀ – угловая частота собственных колебаний управляемого объекта.

При переходе к правильной форме Коши, система уравнений (15) приобретает следующий вид:

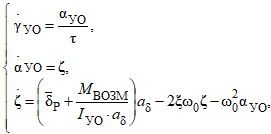где ζ – дополнительно введённая вспомогательная переменная.

Начальное значение курсового угла ракеты , соответствующего моменту времени отделения ракеты от носителя, задаётся в виде соответствующего начального условия системы (16).

Управление летательным аппаратом (ЛА) осуществляется с помощью автопилота, т. е. бортового устройства, осуществляющего отклонение рулей с целью обеспечения заданной траектории. Автопилот является составной частью системы управления и содержит каналы управления курсом, тангажом и креном. У крестокрылых ЛА каналы управления курсом и тангажом аналогичны и работают независимо друг от друга.

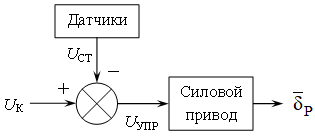
Рассматривается курсовой канал автопилота. Он состоит из исполнительного устройства – силового привода (СП), разностного звена (сумматора с вычитающим входом) и системы чувствительных элементов (датчиков), контролирующих положение ЛА (рис. 9).

Рис. 9 – Схема автопилота ракеты

 

Путём суммирования командного U_К и стабилизирующего U_СТ напряжений образуется управляющее напряжение U_УПР = U_К – U_СТ. Выходным параметром системы является угол отклонения рулей .

Силовой привод предназначен для отклонения рулей УО на угол  пропорционально управляющему напряжению U_УПР. Он представляется в виде замкнутой следящей системы, состоящей из электродвигателя, редуктора и датчика угла отклонения руля, расположенного в цепи отрицательной обратной связи системы, выполняющего роль преобразователя «угол-напряжение». Все элементы безынерционны. При подаче напряжения на электродвигатель, он начинает вращаться. Вращение вала электродвигателя через редуктор приводит к отклонению рулей. Датчик угла отклонения руля формирует напряжение, противоположное по знаку управляющему. За счёт отрицательной обратной связи руль фиксируется под углом .

Таким образом, модель силового привода представляется безынерционным звеном с коэффициентом передачи K_СП.

Особенностью звена СП является нелинейность типа «ограничение», так как рулевые органы имеют предел отклонения рулей, связанный с допустимыми перегрузками и устойчивостью полёта.

Автопилот обеспечивает:

- стабилизацию ЛА и демпфирование возмущающих воздействий;

- обеспечение заданной траектории путём связи сигнала команды системы наведения U_К с углом отклонения рулей ;

- стабилизацию передаточных чисел УО (т. е. коэффициентов пропорциональности между командным сигналом и углами отклонения рулей).

Датчики являются автономными чувствительными элементами, предназначенными для выработки стабилизирующих сигналов. Поскольку пропорциональное наведение применяется для поражения быстродвижущихся и маневрирующих целей, жёсткая обратная связь в автопилоте ракеты не используется. Для простоты в автопилоте упущена также и обратная связь на основе датчика линейных ускорений. Таким образом, рассматривается модель автопилота только с гибкой обратной связью, то есть через скоростной гироскоп с коэффициентом передачи K_СКГ. Выходной сигнал гироскопа, который и будет стабилизирующим сигналом, определяется следующим образом:

    (17)

Движение цели – по окружности с постоянной скоростью V_Ц и постоянной нормальной перегрузкой n_Ц (в частности – прямолинейное и равномерное, когда n_Ц = 0). Тогда дифференциальное уравнение, описывающее динамику движения цели, имеет следующий вид:

    (18)

где g = 9,81 м/с² – ускорение свободного падения вблизи поверхности Земли, а знак « ± » обусловлен направлением движения цели.

Начальное значение курсового угла цели  задаётся в виде соответствующего начального условия уравнения  (18).

Движение носителя – прямолинейное с постоянной скоростью V_Н и постоянным курсовым углом γ_Н. Тогда текущие координаты носителя в плоскости наведения определяются следующим образом:

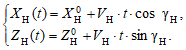    (19)

Полёт носителя до момента отделения ракеты моделируется в течение заданного времени ∆T = 25 сек. При этом его курсовой угол в момент отделения равен начальному курсовому углу ракеты, то есть . Поэтому координаты носителя для момента начала моделирования  были выбраны такими, чтобы к моменту отделения ракеты они соответствовали заданным начальным координатам ракеты  на момент её отделения, то есть:

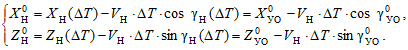    (20)

Таким образом, модель контура управления описывается семью дифференциальными уравнениями первого порядка, представленными в правильной форме Коши:

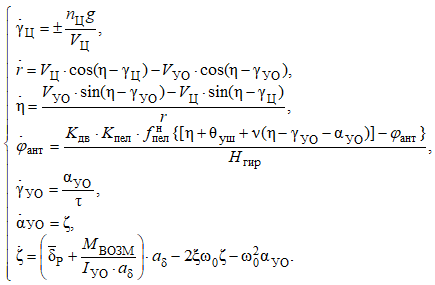    (21)

Численное решение уравнений (21) позволяет определить основные фазовые переменные модели, характеризующие процесс наведения ракеты на цель. Решение уравнений в модели осуществляется методом Рунге-Кутты четвёртого порядка с фиксированным шагом интегрирования [2, С. 259].

Для построения траекторий движения носителя, ракеты и цели в земной системе координат, необходимо получить выражения для их координат как функций времени, то есть {X_Н(t), Z_Н(t)}, {X_УО(t), Z_УО(t)}, {X_Ц(t), Z_Ц(t)}. При этом траектории движения представляют собой зависимости вида:

Z_Н = F₁(X_Н), Z_УО = F₂(X_УО), Z_Ц = F₃(X_Ц).

Выражения для координат {X_Н(t), Z_Н(t)} носителя были рассмотрены ранее и описываются соотношениями (19) и (20).

Для получения выражений для координат ракеты {X_УО(t), Z_УО(t)} и цели {X_Ц(t), Z_Ц(t)}, необходимо сформировать проекции векторов их скоростей на оси OX_зем и OZ_зем земной системы координат, что иллюстрируется рис. 2. В соответствии с рис. 2 эти проекции выражаются следующим образом:

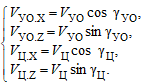   (22) Тогда выражения для текущих координат образуются путём интегрирования по времени составляющих (22): 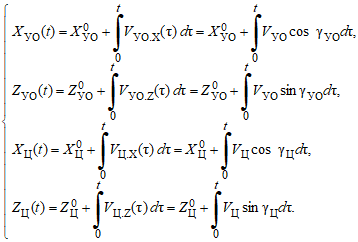    (23)

Начальные координаты ракеты , соответствующие моменту времени отделения ракеты от носителя, были выбраны таким образом, чтобы начальная дальность по линии визирования r₀ соответствовала дальности пуска ракеты (примерно 110 км), а именно  

Результаты моделирования

В результате моделирования были исследованы свойства контура управления при наведении на цель, совершающую манёвр с заданной нормальной перегрузкой n_Ц = 2 и 2,5 ед. п., получены основные фазовые переменные модели, характеризующие процесс наведения ракеты на цель с момента отделения от носителя до встречи с целью при отсутствии углового шума цели (рис. 10 – 18) и при его наличии (рис. 24 – 31).

Представлены смоделированные траектории движения носителя, ракеты и цели в плоскости наведения (рис. 19 – 22).

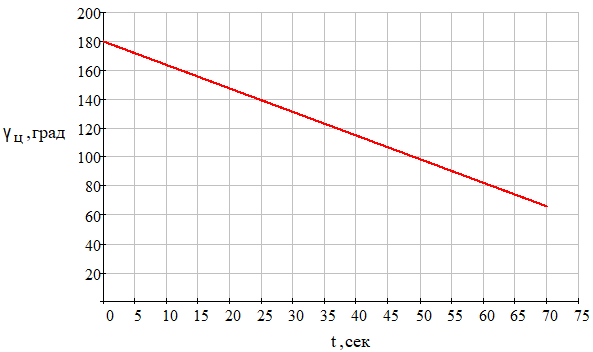
Рис. 10 – Зависимость курсового угла цели от времени

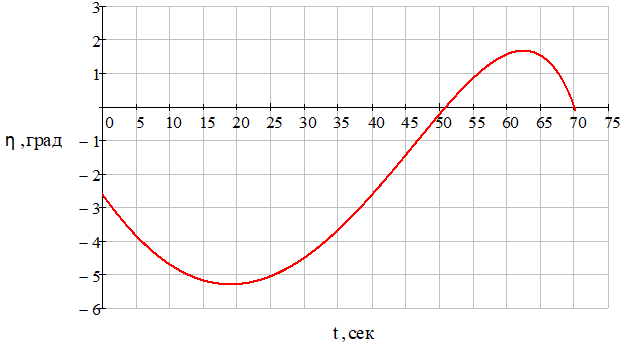
Рис. 11 – Зависимость угла поворота линии визирования от времени при отсутствии углового шума цели

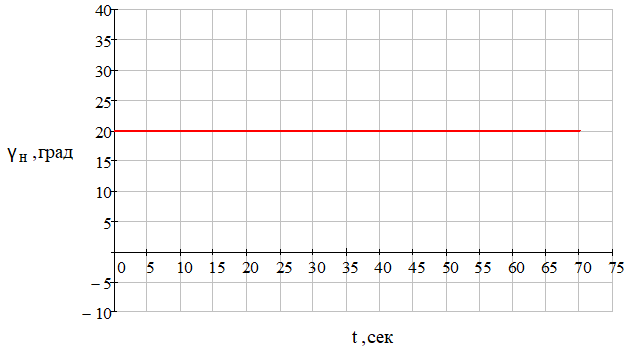
Рис. 12 – Зависимость курсового угла носителя от времени

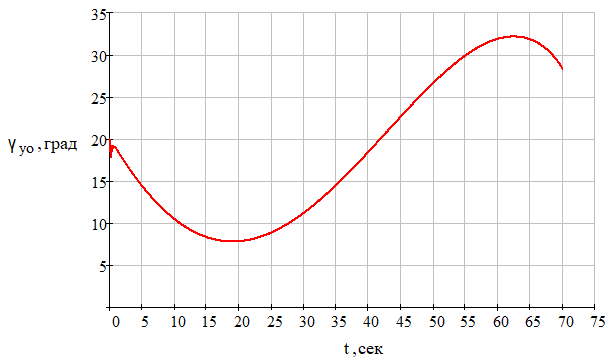
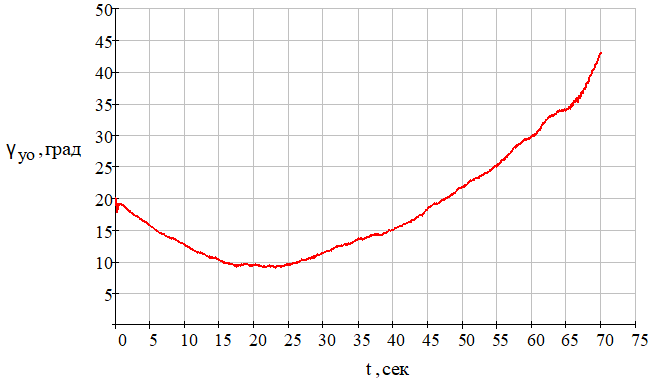
Рис. 13 – Зависимость курсового угла управляемого объекта (ракеты) от времени при отсутствии углового шума цели

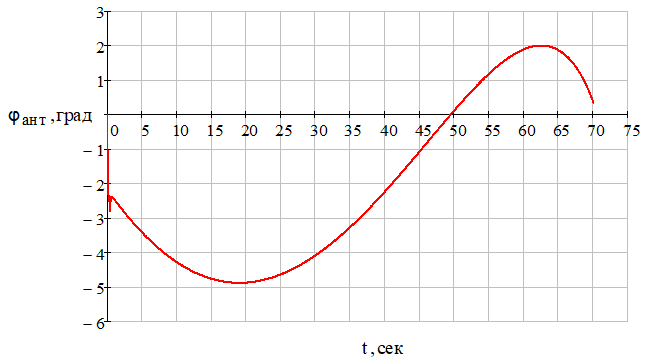
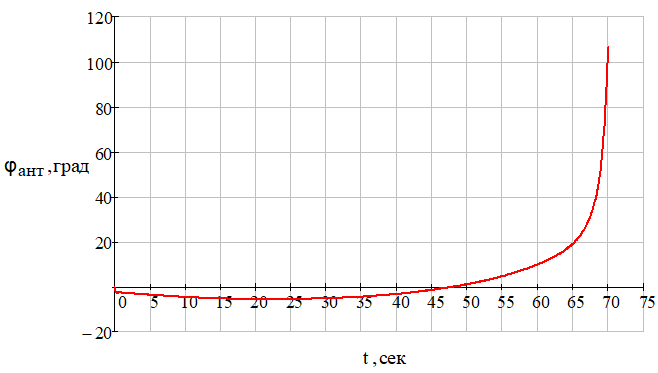
Рис. 14 – Зависимость угла поворота следящего элемента пеленгатора ГСН управляемого объекта (ракеты) от времени при отсутствии углового шума цели

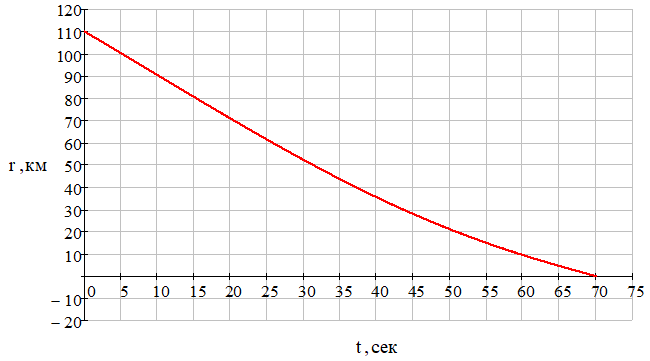
Рис. 15 – Зависимость относительной дальности «ракета – цель» от времени

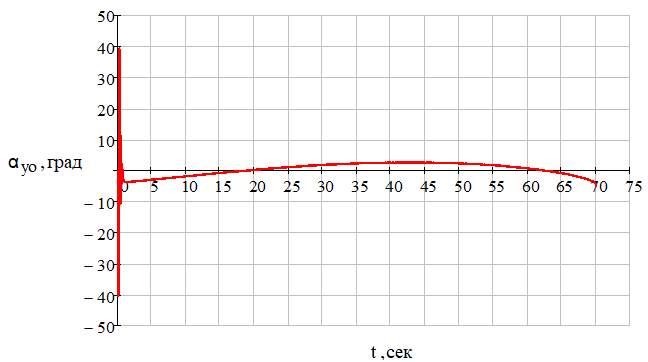
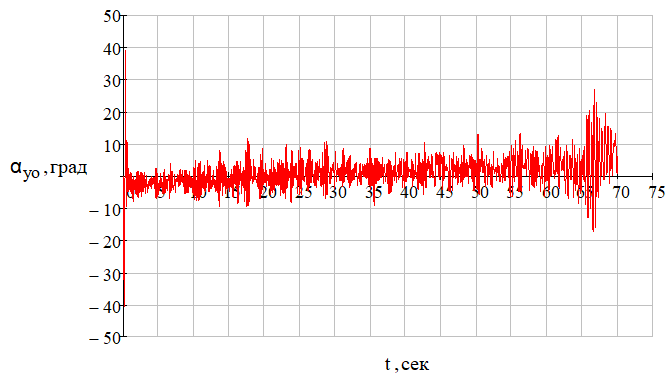
Рис. 16 – Зависимость угла скольжения управляемого объекта (ракеты) от времени при отсутствии углового шума цели

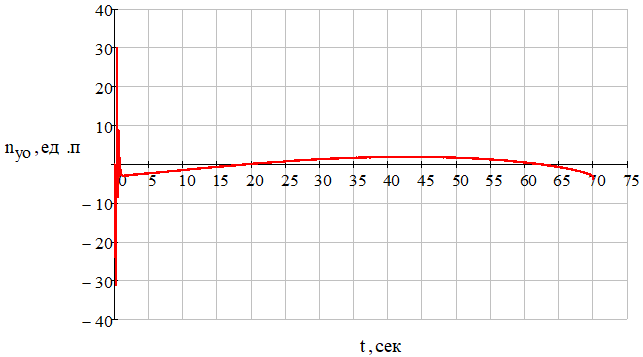
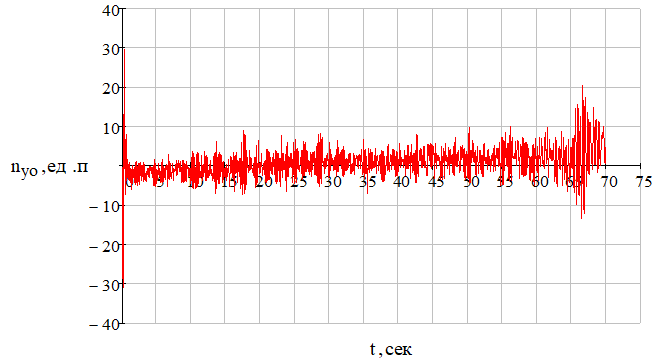
Рис. 17 – Зависимость текущей нормальной перегрузки управляемого объекта (ракеты) от времени при отсутствии углового шума цели

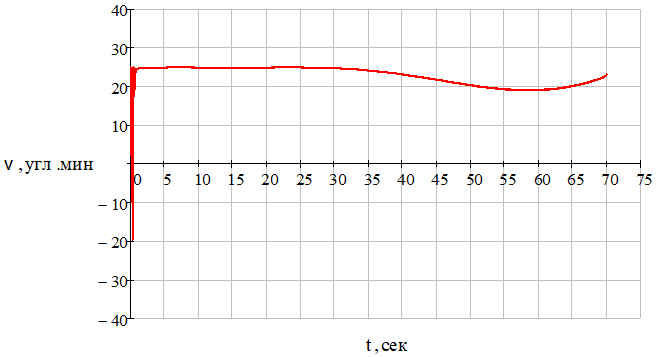
Рис. 18 – Зависимость угловой ошибки, вносимой антенным обтекателем ракеты от времени при отсутствии углового шума цели

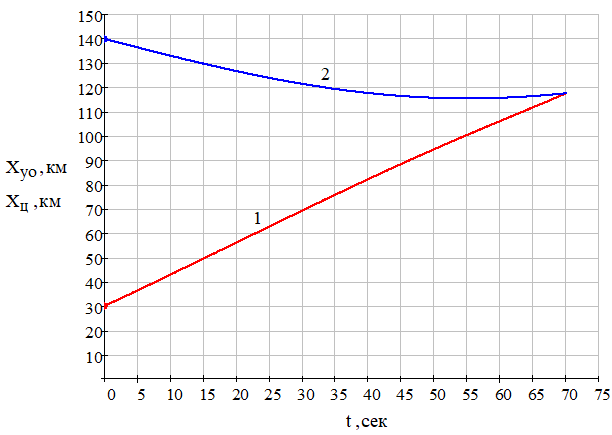
Рис. 19 – Зависимость текущих координат X управляемого объекта (ракеты) (1) и цели (2) от времени

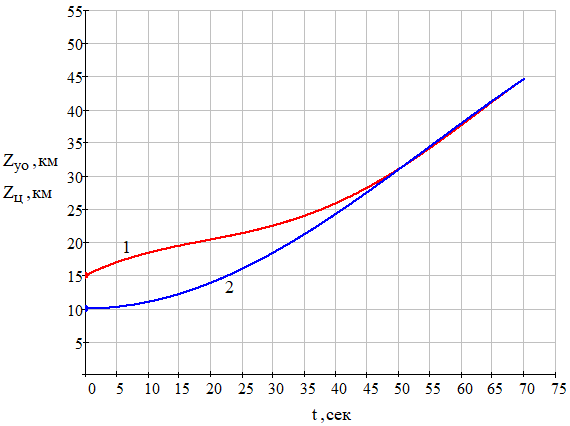
Рис. 20 – Зависимость текущих координат Z управляемого объекта (ракеты) (1) и цели (2) от времени

 

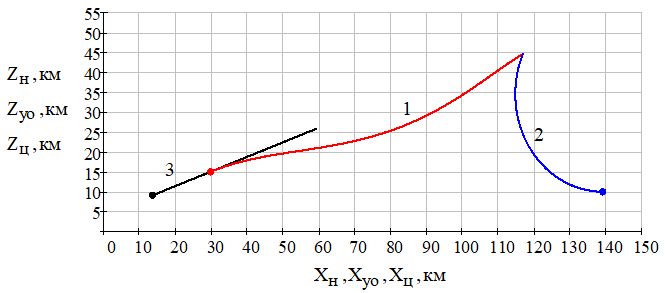
Траектории движения носителя, ракеты и цели с нанесёнными на них начальными координатами при n_Ц = 2 ед. п. приведены на рис. 21.

Рис.21 – Траектории движения управляемого объекта (1), цели (2) и носителя (3) в плоскости наведения в земной системе координат при n_Ц = 2 ед. п.

 

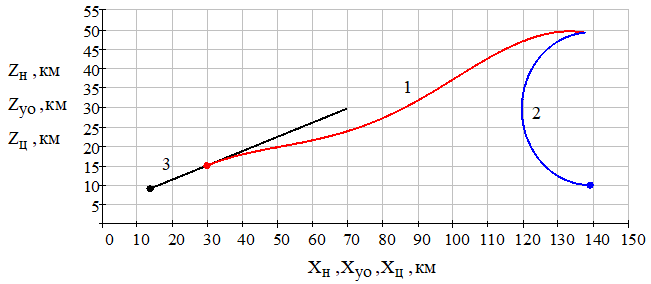
Траектории движения носителя, ракеты и цели с нанесёнными на них начальными координатами при n_Ц = 2,5 ед. п. приведены на рис. 22.

Рис. 22 – Траектории движения управляемого объекта (1), цели (2) и носителя (3) в плоскости наведения в земной системе координат при n_Ц = 2,5 ед. п.

 

Оценка точности наведения выполнялась по исходным данным о конечном взаимном положении ракеты и цели, полученным в результате статистического моделирования процессов наведения. Условия в момент пуска ракеты и результаты моделирования приведены в таблице 1, где приняты следующие обозначения:

Н – высота горизонтального полёта,

V_Н – скорость движения носителя,

γ_Н – курсовой угол носителя,

V_УО – скорость движения управляемого объекта (ракеты),

 – начальный курсовой угол УО,

V_Ц – скорость движения цели,

 – начальный курсовой угол цели,

n_Ц – заданная перегрузка цели,

М_∆r – математическое ожидание (МО) промаха ∆r ракеты относительно цели,

σ_∆r – среднеквадратическое отклонение (СКО) промаха,

Оценка МО и СКО промаха выполнялась по десяти реализациям пуска ракеты (табл. 1).

Таблица 1 – Результаты по оценке точности наведения ракеты при отсутствии углового шума цели

№ п/п	H, км	VН, Мах	γН	VУО, Мах		VЦ, Мах		nЦ, ед. п.	Промах ∆r, м
									M∆r	σ∆r
1	5	2,35	10°	4,5	10°	2,35	0°	0	1,102	0,126
2	5	2,35	10°	4,5	10°	2,35	30°	0	1,203	0,115
3	10	2,35	10°	4,5	10°	2,35	60°	0	1,416	0,201
4	10	2,35	15°	4,5	15°	2,35	90°	1,0	1,821	0,225
5	15	2,35	15°	4,5	15°	2,35	180°	1,0	2,024	0,161
6	15	2,35	15°	4,5	15°	2,35	30°	1,0	2,158	0,253
7	20	2,35	20°	4,5	20°	2,35	90°	2,0	2,236	0,256
8	20	2,35	20°	4,5	20°	2,35	180°	2,0	2,321	0,121
9	25	2,35	20°	4,5	20°	2,35	0°	2,5	2,451	0,237
10	25	2,35	20°	4,5	20°	2,35	60°	2,5	2,482	0,189

 

Анализ результатов, приведённых в таблице 1, а также анализ процессов наведения, показывает следующее.

При отсутствии углового шума цели обеспечивается достаточно высокая точность наведения, характеризуемая математическим ожиданием промаха M_∆r ≈ 1,1 ÷ 2,4 м и среднеквадратическим отклонением σ_∆r ≈ 0,1 ÷ 0,2 м.

Угловой шум цели, порождаемый случайными перемещениями линии визирования вследствие того, что цель перестаёт быть точечным объектом, представлен на рис. 23.

Рис. 23 – Угловой шум цели, как нестационарный по дисперсии случайный процесс, нарастающий по мере сближения с целью

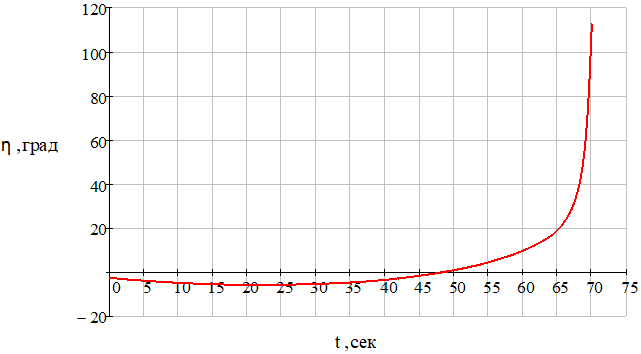
Рис. 24 – Зависимость угла поворота линии визирования от времени при наличии углового шума цели

Рис. 25 – Зависимость курсового угла управляемого объекта (ракеты) от времени при наличии углового шума цели

Рис. 26 – Зависимость угла поворота следящего элемента пеленгатора ГСН управляемого объекта (ракеты) от времени при наличии углового шума цели

Рис. 27 – Зависимость угла скольжения управляемого объекта (ракеты) от времени при наличии углового шума цели

Рис. 28 – Зависимость текущей нормальной перегрузки управляемого объекта (ракеты) от времени при наличии углового шума цели

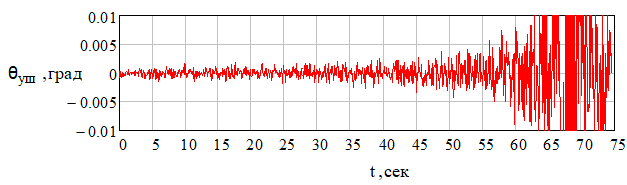
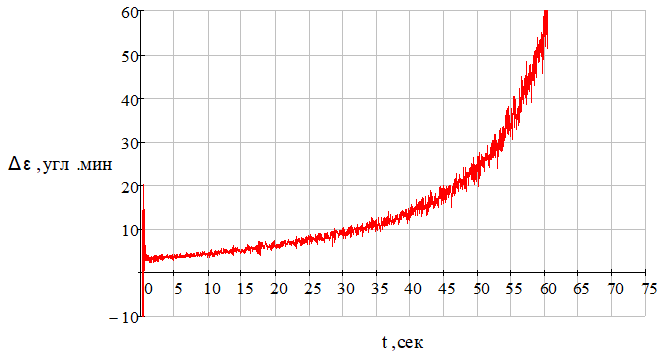
Рис. 29 – Зависимость угловой ошибки, вносимой антенным обтекателем ракеты от времени при наличии углового шума цели

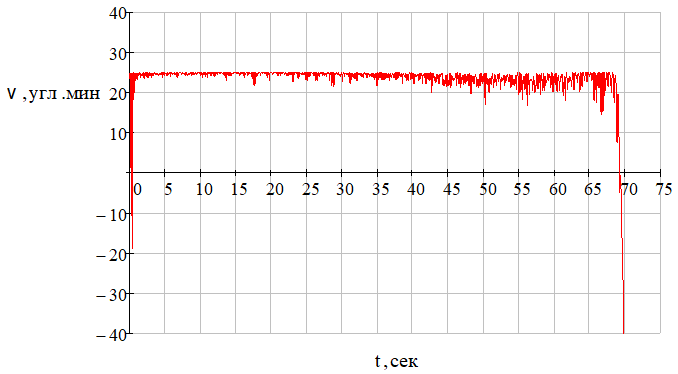
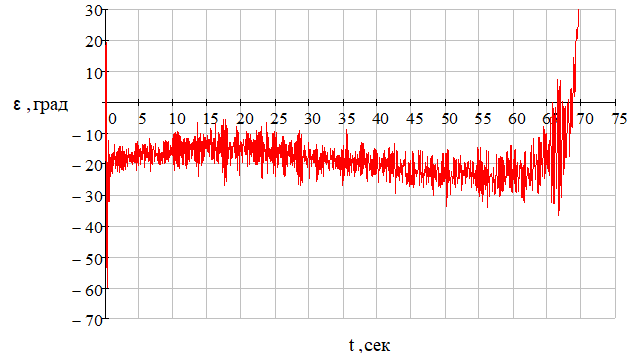
Рис. 30 – Зависимость угла пеленга цели от времени при наличии углового шума

Рис. 31 – Зависимость ошибки слежения по углу (ошибки пеленгования цели) от времени при наличии углового шума

 

Оценка МО и СКО промаха при действии углового шума цели выполнялась аналогично по десяти реализациям пуска ракеты (табл. 2).

 

Таблица 2 – Результаты по оценке точности наведения ракеты при наличии углового шума цели

№ п/п	H, км	VН, Мах	γН	VУО, Мах		VЦ, Мах		nЦ, ед. п.	Промах ∆r, м
									M∆r	σ∆r
1	5	2,35	10°	4,5	10°	2,35	0°	0	5,509	1,213
2	5	2,35	10°	4,5	10°	2,35	30°	0	5,813	1,227
3	10	2,35	10°	4,5	10°	2,35	60°	0	6,246	1,504
4	10	2,35	15°	4,5	15°	2,35	90°	1,0	6,651	1,545
5	15	2,35	15°	4,5	15°	2,35	180°	1,0	7,097	1,612
6	15	2,35	15°	4,5	15°	2,35	30°	1,0	7,491	1,698
7	20	2,35	20°	4,5	20°	2,35	90°	2,0	8,102	1,721
8	20	2,35	20°	4,5	20°	2,35	180°	2,0	8,382	1,789
9	25	2,35	20°	4,5	20°	2,35	0°	2,5	9,083	1,802
10	25	2,35	20°	4,5	20°	2,35	60°	2,5	9,503	1,876

 

Анализ результатов, приведённых в таблице 2, а также анализ процессов наведения, показывает следующее.

При введении в модель углового шума цели, высокой точности наведения не обеспечивается: математическое ожидание промаха составляет M_∆r ≈ 5,5 ÷ 9,5 м, среднеквадратическое отклонение σ_∆r ≈ 1,2 ÷ 1,8 м. Низкая точность определяется недостаточной динамикой контура управления и высокой чувствительностью к воздействию случайных флюктуаций углового шума цели. Временное запаздывание контура в отработке заданной перегрузки при подлёте к цели достигает τ_З ≈ 0,5 ÷ 1 сек.

Заключение

Таким образом, из результатов моделирования следует, что угловой шум цели, может оказывать существенное влияние на точность наведения при различных условиях пуска ракеты и параметрах звеньев контура наведения. Параметры звеньев контура наведения, а также исходные данные для моделирования, задаются, и в дальнейшем могут быть уточнены по результатам анализа реальных (телеметрических) параметров с натурных (практических) работ, проводимых на оценку точности наведения в целях обеспечения сходимости результатов математического моделирования и натурных работ. Для повышения точности наведения в условиях действия углового шума необходимо применение специальных методов обработки радиолокационного сигнала, отражённого от цели, что выходит за рамки моделирования поставленной проблемы и метода моделирования в данной математической модели.

Конфликт интересов	Conflict of Interest
Не указан.	None declared.

 

Список литературы / References

1. Проектирование управляемых авиационных ракет класса «воздух-воздух» (теория, конструкция, технология, испытания, экономика, техника безопасности) в 2-х частях: Учебное пособие / под редакцией Соколовского Г.А. – М.: Изд-во ГосМКБ «Вымпел», 2005. – 1168 с.
2. Вейцель В.А. Радиосистемы управления: Учебник для вузов / В.А. Вейцель, А.С. Волковский, С.А. Волковский и др. Под ред. В.А. Вейцеля. – М.: Дрофа, 2005. – 416 с., ил.
3. Меркулов В.И. Авиационные системы радиоуправления. Т. 2. Радиоэлектронные системы самонаведения / В.И. Меркулов, В.В. Дрогалин, А.И. Канащенков и др. Под ред. А. И. Канащенкова и В. И. Меркулова. – М.: «Радиотехника», 2003. – с.: ил.
4. Радиотехнические системы: Учеб. пособие для вузов по спец. «Радиотехника» / Ю.П. Гришин, В.П. Ипатов, Ю.М. Казаринов и др.; Под ред. Ю.М. Казаринова. – М.: Высш. шк., 1990. – 496 с: ил.
5. Семяшкина М.А. Математические модели систем наведения / М.А. Семяшкина, Д.В. Кошкин // Научное сообщество студентов: Междисциплинарные исследования: сб. ст. по мат. XXXVII междунар. студ. науч.-прак. конф. №2 (37). [Электронный ресурс]. – URL: https://sibac.info/archive/meghdis/2(37).pdf (дата обращения: 09.04.2021).

Список литературы на английском языке / References in English

1. Proektirovanie upravljaemyh aviacionnyh raket klassa «vozduh-vozduh» (teorija, konstrukcija, tehnologija, ispytanija, jekonomika, tehnika bezopasnosti) [Design of guided air-to-air missiles (theory, design, technology, testing, economics, safety)] in 2 parts: Textbook / edited by Sokolovsky G. A.-M.: Publishing house of the GosMKB "Vympel", 2005 – - 1168 p. [in Russian]
2. Weitzel V. A. Radiosistemy upravlenija [Radio control systems]: Textbook for universities / V. A. Weitzel, A. S. Volkovsky, S. A. Volkovsky, etc. Ed. by V. A. Weitzel. - M.: Bustard, 2005 – - 416 p., ill. [in Russian]
3. Merkulov V. I. Aviacionnye sistemy radioupravlenija. T. 2. Radiojelektronnye sistemy samonavedenija [Aviation systems of radio control. Vol. 2. Radioelectronic systems of homing] / V. I. Merkulov, V. V. Drogalin, A. I. Kanashchenkov, etc. Edited by A. I. Kanashchenkov and V. I. Merkulov. - M.: "Radio Engineering", 2003. [in Russian]
4. Radiotehnicheskie sistemy [Radio-technical systems] : Textbook for universities on spec. "Radio Engineering" / Yu. P. Grishin, V. P. Ipatov, Yu. M. Kazarinov, et al.; Edited by Yu. M. Kazarinov. - M.: Higher School of Economics, 1990. - 496 p. [in Russian]
5. Semyashkina M. A. Matematicheskie modeli sistem navedenija [Mathematical models of guidance systems] / M. A. Semyashkina, D. V. Koshkin // Nauchnoe soobshhestvo studentov: Mezhdisciplinarnye issledovanija: sb. st. po mat. XXXVII mezhdunar. stud. nauch.-prak. konf. [Scientific community of students: Interdisciplinary research: sat. st. po mat. XXXVII mezhdunar. stud. nauch. - prak. conf.] No. 2 (37). [Electronic resource]. - URL: https://sibac.info/archive/meghdis/2 (37).pdf (accessed: 09.04.2021). [in Russian]