MATHEMATICAL MODEL OF VISCOSITY OF UNFILLED EPOXY RESIN
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЯЗКОСТИ НЕНАПОЛНЕННОЙ ЭПОКСИДНОЙ СМОЛЫ
Научная статья
Бормотов А.Н.1, *, Горохова А.А.2
1 ORCID: 0000-0001-7069-6603,
1 Пензенский государственный технологический университет, Пенза, Россия;
2 Пензенский государственный университет архитектуры и строительства, Пенза, Россия
* Корреспондирующий автор (aleks21618[at]yandex.ru)
АннотацияПредложен математический метод моделирования полимерных композиционных материалов при помощи функционалов качества кинетических (переходных) процессов. Обоснована целесообразность рассмотрения кинетических (переходных) процессов как необходимого и достаточного признака формирования структуры термореактивного вяжущего. Рассмотрены процессы, протекающие при формировании модифицированного полимера и появление качественно новых свойств при сохранении химической индивидуальности каждого компонента, учитываемые в предложенном функционале качества. Построена математическая модель вязкости ненаполненной эпоксидной смолы ЭД-16.
Ключевые слова: композиционные материалы, математическое моделирование, вязкость, пластификация, оптимизация свойств.
MATHEMATICAL MODEL OF VISCOSITY OF UNFILLED EPOXY RESIN
Research article
Bormotov A.N.1, *, Gorokhova A.A.2
1 ORCID: 0000-0001-7069-6603,
1 Penza State Technological University, Penza, Russia;
2 Penza State University of Architecture and Construction, Penza, Russia
* Corresponding author (aleks21618[at]yandex.ru)
Abstract
The paper proposes a mathematical modeling method for polymer composite materials using the quality functional of kinetic (transient) processes. The expediency of considering kinetic (transient) processes as a necessary and sufficient sign of the formation of a thermosetting binder structure is substantiated. Processes occurring during the formation of the modified polymer and the emergence of qualitatively new properties while maintaining the chemical identity of each component are considered in the proposed quality functional. Mathematical model of the viscosity of unfilled epoxy resin ED-16 is created.
Keywords: composite materials, mathematical modeling, viscosity, plasticization, optimization of properties.
ВведениеЭпоксидная смола марки ЭД-16 представляет собой высоковязкую прозрачную жидкость от светло-жёлтого до коричневого цвета, растворимую в толуоле, ксилоле, кетонах; устойчивую к действию воды, растворов солей, кислот, щелочей и радиоактивного излучения. Эпоксидная смола ЭД-16 по своим реологическим свойствам относится к низковязким ньютоновским жидкостям с вязкостью при 40оС 20000-60000 спз [1]. Эпоксидная смола ЭД-16 в силу своей высокой молекулярной массы более других подходит для приготовления композиционных материалов. Но приготовление различных композиционных материалов на основе смолы ЭД-16 представляет собой очень трудоёмкий процесс, так как при обычной (комнатной) температуре данная смола практически не может быть использована из-за высокой вязкости.
Методы и принципы исследования
Изучение вязкости и действия модификаторов проводилось на вискозиметре ВЗ-4 по стандартной методике.
В ходе исследований была получена экспериментальная зависимость вязкости В(t) от температуры смолы t, которая имеет вид:
| B(t) = A × exp (-b × t), | (1) |
где В (t) – вязкость смолы, сек; t – температура смолы, оС; А и b – постоянные коэффициенты, равные А = 7267,2 и b = – 0,0723.
Уравнение (1) представляет собой модифицированное уравнение текучести Аррениуса:
где B(t) – вязкость; B(ti) – вязкость при i-й температуре; E – энергия активации; R – газовая постоянная; T – температура.
Совершенно очевидно, что уравнение (2) легко трансформируется в уравнение (1). Однако использование уравнения вида (1) позволяет значительно облегчить оценку эффективности действия модификаторов на вязкость смолы.
Визуальная оценка эффективности действия модификаторов затруднена из-за погрешностей определения вязкости, неточности графических построений, произвольности в выборе масштаба, множества сравниваемых кривых и т.д.
Дифференцируя уравнение вязкости вида (1) и приравнивая первую производную к нулю, легко найти тангенс угла (или сам угол) наклона касательной к оси абсцисс в любой точке кривой. Пусть это будет точка 40оС, соответствующая предельной температуре совмещения смолы и отвердителя (рис. 1). Из рис. 1 видно, что ![]() . Это означает, что вязкость системы, описанной функцией «I», будет выше, чем вязкость системы, описанной функцией «II», при температуре 40 оС. При большом количестве опытов и при наличии погрешностей эксперимента такой метод позволяет значительно ускорить процесс анализа данных (за счет применения ЭВМ), а также повысить его качество.
. Это означает, что вязкость системы, описанной функцией «I», будет выше, чем вязкость системы, описанной функцией «II», при температуре 40 оС. При большом количестве опытов и при наличии погрешностей эксперимента такой метод позволяет значительно ускорить процесс анализа данных (за счет применения ЭВМ), а также повысить его качество.
Применяя данный метод, были найдены концентрации пластификаторов и модификаторов.
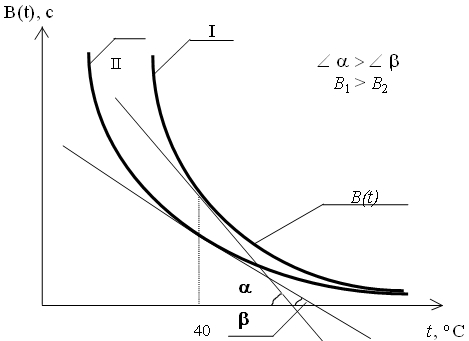
Рис. 1 – Иллюстрация метода определения эффективности действия модификаторов на вязкость ненаполненной смолы ЭД-16
Основные результатыКак известно, существует два метода модификации полимеров путём введения пластифицирующих добавок – молекулярная пластификация и структурная пластификация [2], [3]. Молекулярная пластификация подразумевает изменение механических свойств путём введения в них, в основном, низкомолекулярных веществ, совмещающихся с полимером на молекулярном уровне. Действие таких пластификаторов заключается в том, что благодаря взаимодействию полимера с молекулами пластификатора ослабляются силы взаимодействия макромолекул между собой. Из-за этого появляется возможность взаимной перегруппировки звеньев макромолекул под влиянием внешних механических полей и, соответственно, увеличивается податливость системы. Структурная пластификация связана с эффектом изменения механических свойств при введении относительно малых количеств низкомолекулярных веществ, практически не совместимых с полимером. При этом пластификатор распределяется между элементами структуры в виде тонких слоёв и оказывает своеобразный эффект "смазки".
В данной работе использовались в качестве пластифицирующих добавок следующие вещества: минеральное машинное масло – ММ, растительное масло – РМ, подсолнечное масло – ПМ, ДБФ – дибутилфталат.
На рис. 2 показано, как изменяется вязкость смолы ЭД-16 от добавок оптимальных концентраций масел ПМ, РМ и ММ.
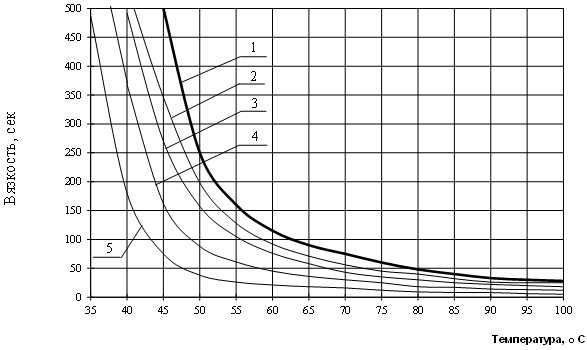
Рис. 2 – Влияние различных пластификаторов оптимальной концентрации на вязкость ненаполненной эпоксидной смолы:
1– чистая смола; 2 – РМ в концентрации 5 %; 3 – ПМ в концентрации 5 %; 4 – ММ в концентрации 10 %; 5 – ДБФ в концентрации 15 %
Химический состав минеральных и растительных масел очень сложен. Они содержат парафиновые, нафтеновые, ароматические, асфальто-смолистые вещества, а также смеси высоконепредельных, непредельных и предельных жирных кислот с рядом других углеводородов. Часть этих веществ по отношению к эпоксидной смоле являются реакционноспособными пластификаторами и осуществляют молекулярную пластификацию, другая же часть практически несовместима с эпоксидной смолой и выступает в качестве структурных пластификаторов. Поэтому, в случае использования модификаторов типа ММ, ПМ и РМ, имеет место комплексная пластификация. Некоторая часть молекул пластификатора ММ вступает во взаимодействие с молекулами полимера, ослабляя силы взаимодействия макромолекул между собой. Одновременно другая часть молекул пластификатора ММ своими углеводородными радикалами раздвигают цепи макромолекул полимера, создавая плоскости проскальзывания [3], [4].
С целью описания процессов пластификации полимерных материалов представляется перспективным использование динамических моделей, определённых в классе дифференциальных уравнений. Для гомогенных систем такая модель в классе обыкновенных дифференциальных уравнений рассматривается в [5], [6], [7]. Повышение порядка дифференциального уравнения позволяет описать кинетические процессы в гетерогенных, дисперсных и полидисперсных системах для многих контролируемых параметров [8, 9]. При этом, как правило, оказывается возможным ограничиться классом обыкновенных дифференциальных уравнений с постоянными коэффициентами [10]. В частности, для процессов вида, приводимого на рис. 3, с асимптотическим выходом контролируемого параметра на эксплуатационное значение можно использовать модель вида:
где ![]() – модули корней (отрицательных) характеристического полинома.
– модули корней (отрицательных) характеристического полинома.
Значение l2 можно определить по концу переходного процесса. Можно показать справедливость соотношения ![]() . Оно позволяет определить значение λ1, а стало быть, и процесс x(t).
. Оно позволяет определить значение λ1, а стало быть, и процесс x(t).
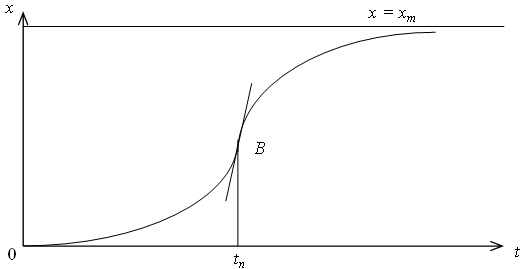
Рис. 3 – Вид кинетического процесса
Экспериментально легко определить зависимости λ1, λ2, xm (то есть процесс x(t)) от параметров модели wo и n (вместо n можно использовать безразмерный коэффициент демпфирования ![]() ), с учётом корреляционных связей между λi и Ф(S).
), с учётом корреляционных связей между λi и Ф(S).
Для высоковязких материалов, на основе смолы ЭД-16 в частности, нет теоретических аспектов пластификации этих систем и, естественно, отсутствуют оптимальные рецептурно-технологические параметры композиций. Поэтому при практической апробации метода определялись оптимальные концентрации пластификаторов и модификаторов.
Самой простой, но и достаточно грубой, является ступенчатая аппроксимация. Ее можно применять или при мелкой сетке в пространстве аргумента x, или при специальном ступенчатом виде самой функции.
При создании математической модели вязкости ненаполненной эпоксидной смолы задача приближения функции нескольких переменных может решаться на основе метода наименьших квадратов, представляя ее суммой одной переменной.
Для случая функции двух переменных ![]() с прямоугольной областью изменения аргументов
с прямоугольной областью изменения аргументов
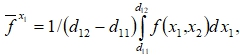 (7)
(7)
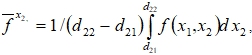 (8)
(8)
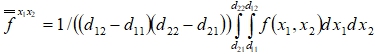 (9)
(9)
В случае приближения ![]() в виде произведения двух одномерных функций, введя
в виде произведения двух одномерных функций, введя ![]() и выполнив приближение этой функции суммой
и выполнив приближение этой функции суммой ![]() , получаем:
, получаем:
где ![]() .
.
На основе описанных выше решений предлагается новый математический метод моделирования многомерных таблично заданных функций обобщенными многочленами при получении математической модели вязкости ненаполненной эпоксидной смолы. В частности, при двумерной аппроксимации аппроксимирующий многочлен определяется в виде:
где ![]() – функции, выбранные по экспериментальным данным.
– функции, выбранные по экспериментальным данным.
Тогда коэффициенты ![]() определяются из условия минимума
определяются из условия минимума
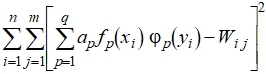 (12)
где
(12)
где 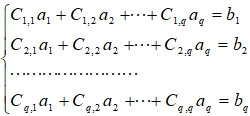 (13)
Здесь
(13)
Здесь
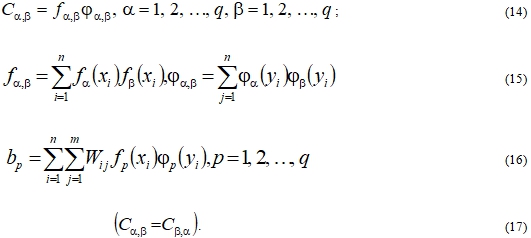
В табл. 1 приводятся данные по определению зависимости вязкости В связующего на основе эпоксидной смолы ЭД-16 от температуры t °C и специальных добавок (ММ) в различных концентрациях x, %.
Таблица 1 – Зависимость вязкости (с) эпоксидного связующего от температуры и процентного содержания пластификатора (ММ)
| t, °C x, % | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 0 | 172 | 119 | 84 | 65 | 50 | 40 | 30 | 25 | 22 | 20 | 19 |
| 1 | 210 | 145 | 105 | 80 | 65 | 52 | 43 | 35 | 30 | 27 | 25 |
| 5 | 250 | 160 | 115 | 90 | 75 | 60 | 48 | 40 | 33 | 30 | 28 |
| 10 | 97 | 65 | 45 | 33 | 22 | 17 | 13 | 10 | 11 | 9 | 8 |
| 15 | 132 | 91 | 62 | 47 | 36 | 30 | 21 | 18 | 17 | 15 | 12 |
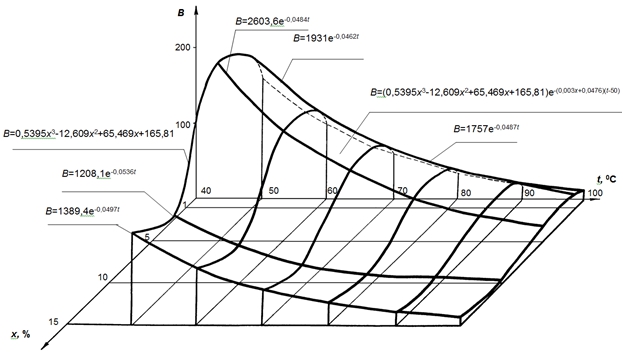
Рис. 4 – Двухфакторная зависимость вязкости эпоксидных композитов от температуры и процентного содержания ММ
Математическая модель вязкости ненаполненной эпоксидной смолы, согласно представленному выше математическому методу моделирования вязкости, может быть получена в виде:
Заключение
Как видно из рис. 4, оптимальная концентрация пластификатора составляет 10% от массы смолы, а это значит, что на 2-4 молекулы смолы приходится 1 молекула пластификатора. Такое количественное соотношение веществ характерно, например, для реакции поликонденсации между эпоксидной смолой и алифатическими аминами (ПЭПА). Следовательно, будет справедливо предположить взаимодействие между макромолекулами эпоксидной смолы и реакционно-способными составляющими пластификатора ММ, что доказывает эффект молекулярной пластификации. Кривые вязкости, полученные с использованием ММ, приближаются к кривым, полученным с использованием традиционного нереакционного пластификатора – дибутилфталата (рис. 2). Это, в свою очередь, доказывает присутствие эффекта структурной пластификации. Однако, в отличие от случая применения ДБФ, машинное масло в эпоксидной смоле способствует поперечным сшивкам, хорошо распределяется в массе смолы, что не приводит к резкому разупрочнению структуры. Известно, что эпоксидные полимеры обладают статической клубкообразной конформацией с сильным переплетением цепей на молекулярном уровне [11]. Введение небольших количеств пластификатора (1-5%) приводит к образованию агрегатов из эпоксидных олигомеров и реакционноспособной части пластификатора ММ, что вызывает некоторое увеличение вязкости системы. Дальнейшее увеличение концентрации пластификатора до 10-15 % приводит к дроблению образованных агрегатов, появлению более мелких глобул и пачек и снижению сил трения между новообразованиями, клубками и отдельными молекулами эпоксидного олигомера, приводя к эффективной молекулярной и структурной пластификации системы. Эффектом комплексной пластификации также можно объяснить и тот факт, что при введении в систему пластификатора ММ снижение физико-механических свойств не превышает 10%, в то время как при использовании пластификатора ДБФ – эти свойства уменьшаются на 35-40%.
Предложенные математические методы и модели позволяют эффективно решать задачу пластификации высоковязких полимеров при помощи функционалов качества кинетических (переходных) процессов с целью многокритериального синтеза полимерных композиционных материалов.
| Конфликт интересов Не указан | Conflict of Interest None declared |
Список литературы / References
- Энциклопедия полимеров / Под ред. В.А. Кабанова. – Т. III. – М.: Издательство "Советская энциклопедия", 1977. – С. 992-998.
- Еремеева М.А. Исследование отверждения эпоксидных смол в присутствии поверхностно-активных веществ и наполнителя / М.А. Еремеева, И.М. Юрьевская, Г.Н. Кузнецова и др. // Работоспособность композиционных строительных материалов в условиях воздействия различных эксплуатационных факторов. – Казань: КИСИ, – С. 61-64.
- Иржак В.П. Особенности кинетики формирования сетчатых полимеров / Иржак В.П., Розенберг Б.А // ВМС. – 1985. – Т. (А), ХХVII, № 9. – С. 1795-1806.
- Иржак В.П. Сетчатые полимеры. Синтез, структура, свойства / В.А. Иржак, Б.А. Розенберг, Н.С. Ениколопян. – М.: Наука, – 248 с.
- Бормотов А.Н. Математическое моделирование и многокритериальный синтез композиционных материалов / А.Н. Бормотов, И.А. Прошин, Е.В. Королев. – Пенза, Изд-во ПГТА, 2011. – 352 с.
- Бормотов А.Н. Математическое моделирование и многокритериальный синтез композиционных материалов специального назначения : дис. … док. техн. наук : 05.13.18 : защищена 21.12.2011 : утв. 30.08.2012 / Бормотов Алексей Николаевич. – Пенза, Пензенский государственный технологический университет, 2011 – 316 с.
- Бормотов А.Н. Полимерные композиционные материалы для защиты от радиации : монография. – М., Палеотип, 2012. – 272 с.
- Бормотов А.Н. Исследование математических моделей структурообразования композиционных материалов аналитическими методами / А.Н. Бормотов, И.А. Прошин, А.В. Васильков // Вестник Брянского государственного технического университета. – 2011.– №2 (30). – С. 62-70.
- Бормотов А.Н. Исследование реологических свойств композиционных материалов методами системного анализа / А.Н. Бормотов, И.А. Прошин // Вестник Тамбовского государственного технического университета. – 2009. – Т. 15.– № – С. 916-925.
- Proshin A.P. The Extra-Heavy Concrete For Protection From Radiation / P. Proshin, E.V. Korolev, A.N. Bormotov, O.L. Figovsky //Proceedings of the International Conference on Role of Concrete in Nuclear Facilities2005 International Congress – Global Construction: Ultimate Concrete Opportunities. Ser. "Role of Concrete in Nuclear Facilities – Proceedings of the International Conference". – University of Dundee, Concrete Technology Unit. Dundee, Scotland, 2005. – С. 69-76.
- Тагер А.А. Физикохимия полимеров. – М.: Химия, – 544 с.
Список литературы на английском языке / References in English
- Enciklopediya polimerov [Encyclopedia of Polymers] / Edited by V.A. Kabanova. – V. III. – M.: Iz-datel'stvo "Sovetskaya enciklopediya" [Soviet encyclopedia], 1977. – P. 992-998. [in Russian]
- Eremeeva M.A. Issledovanie otverzhdeniya epoksidnyh smol v prisutstvii poverhnostno-aktivnyh veshchestv i napolnitelya [The study of curing of epoxy resins in the presence of surfactants and filler] / M.A. Eremeeva, I.M. YUr'evskaya, G.N. Kuznecova and others // Rabotosposobnost' kompozicionnyh stroitel'nyh materialov v usloviyah vozdejstviya razlichnyh ekspluatacionnyh faktorov [Efficiency of composite building materials under the influence of various operational factors]. – Kazan: KIBI, 1982. – P. 61-64. [in Russian]
- Irzhak V.P.Osobennosti kinetiki formirovaniya setcha-tyh polimerov [Features of the kinetics of the formation of cross-linked polymers.] / Irzhak V.P., Rozenberg B.A. // VMS. – 1985. – V. (A), XXVII, № 9. – P. 1795-1806. [in Russian]
- Irzhak V.P. Setchatye polimery. Sintez, struktura, svojstva [Reticulated polymers. Synthesis, structure, properties] / A. Irzhak, B.A. Rozenberg, N.S. Enikolopyan. – M.: Nauka, 1979. – 248 p. [in Russian]
- Bormotov A.N. Matematicheskoe modelirovanie i mnogokriterial'nyj sintez kompozicionnyh materialov [Mathematical modeling and multicriteria synthesis of composite materials] / A.N. Bormotov, I.A. Proshin, E.V. Korolev. – Penza, Izd-vo PGTA [Publishing house PSTA], 2011. – 352 p. [in Russian]
- Bormotov A.N. Matematicheskoe modelirovanie i mnogokriterial'nyj sintez kompozicionnyh materialov special'nogo naznacheniya [Mathematical modeling and multicriteria synthesis of composite materials for special purposes] : dis. … of PhD in Engineering : 05.13.18 : defense of the thesis 21.12.2011 : approved 30.08.2012 / Bormotov Aleksej Nikolaevich [Bormotov Alexey Nikolaevich]. – Penza, Penzenskij gosudarstvennyj tekhnologicheskij universitet [Penza State Technological University], 2011 – 316 p. [in Russian]
- Bormotov A.N. Polimernye kompozicionnye materialy dlya zashchity ot radiacii : monografiya [Polymeric composite materials for radiation protection: monograph]. – M., Paleotip [Paleotype], 2012. – 272 p. [in Russian]
- Bormotov A.N. Issledovanie matematicheskih modelej strukturoobrazovaniya kompozicionnyh materialov analiticheskimi metodami [Research of mathematical models of structure formation of composite materials by analytical methods] / A.N. Bormotov, I.A. Proshin, A.V. Vasil'kov // Vestnik Bryanskogo gosudarstvennogo tekhnicheskogo universiteta [Bulletin of the Bryansk State Technical University]. – 2011. – № 2 (30). – P. 62-70. [in Russian]
- Bormotov A.N. Issledovanie reologicheskih svojstv kompozicionnyh materialov metodami sistemnogo analiza [The study of the rheological properties of composite materials by systems analysis] / A.N. Bormotov, I.A. Proshin // Vestnik Tambovskogo gosudarstvennogo tekhnicheskogo universiteta [Bulletin of the Tambov State Technical University]. – 2009. – V. 15. – № 4. – P. 916-925. [in Russian]
- Proshin A.P. The Extra-Heavy Concrete For Protection From Radiation / P. Proshin, E.V. Korolev, A.N. Bormotov, O.L. Figovsky //Proceedings of the International Conference on Role of Concrete in Nuclear Facilities2005 International Congress – Global Construction: Ultimate Concrete Opportunities. Ser. "Role of Concrete in Nuclear Facilities – Proceedings of the International Conference". – University of Dundee, Concrete Technology Unit. Dundee, Scotland, 2005. – С. 69-76. [in English]
- Tager A.A. Fizikohimiya polimerov [Physicochemistry of polymers]. – M.: Himiya, 1976. – 544 p. [in Russian]