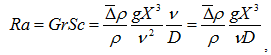INFLUENCE OF GRAVITY CONVECTION TO TRANSFER IN ELECTROMEMBRANE SYSTEMS FOR CLEANING MASSIVE GROUND AND SEWAGE WATER

Антониади Д.Г.¹, Лаврентьев А.В. ²

¹Доктор технических наук, профессор, ²ORCID: 0000-0002-4701-2020, докторант, Кубанский государственный технологический университет

ВЛИЯНИЕ ГРАВИТАЦИОННОЙ КОНВЕКЦИИ НА ПЕРЕНОС В ЭЛЕКТРОМЕМБРАННЫХ СИСТЕМАХ ОЧИСТКИ ПЛАСТОВЫХ И СТОЧНЫХ ВОД

Аннотация

Показано, что успешного применения электромембранных систем требуется глубокое понимание процессов массопереноса в этих системах. Отсюда возникает необходимость в построении адекватных математических моделей различных видов конвективных течений и исследовании основных закономерностей переноса в этих условиях. Проведен анализ большого количества работ, посвященных построению и исследованию математических моделей электрохимических систем с учетом гравитационной конвекции. Установлено, что в этих работах ограничиваются рассмотрением сравнительно простых математических моделей при различных упрощающих предположениях. В частности, в них изучен в основном стационарный перенос, не рассматривается вынужденная конвекция и перенос тепла через мембрану, имеющие важное значение в ряде случаев. Следовательно, сегодняшний день не существует математических моделей, достаточно адекватно описывающих нестационарные неизотермические процессы переноса в электромембранных системах с учетом совместного действия различных видов конвекции, что и определяет актуальность данной работы.

Ключевые слова: электромембранные системы, перенос ионов, математические модели, гравитационная конвекция.

 

Antoniady D.G.¹, Lavrentiev A.V.²

¹PhD in Engineering, professor, ²ORCID: 0000-0002-4701-2020, Doctoral student, Kuban State Technological University

INFLUENCE OF GRAVITY CONVECTION TO TRANSFER IN ELECTROMEMBRANE SYSTEMS FOR CLEANING MASSIVE GROUND AND SEWAGE WATER

Abstract

It is shown that the successful application of electro systems require a deep understanding processes of mass transfer in these systems. This makes it necessary to construct an adequate mathematical models of different types of convective flows and study the basic laws of transport in these conditions. The analysis of a large number of works devoted to the the construction and investigation of mathematical models of electrochemical systems with regard the gravity convection. It was found that in these works are limited to the consideration of comparatively simple mathematical models at various simplifying assumptions. In particular, they studied mainly stationary transfer is not considered and forced convection heat transfer through the membrane, which are important in several cases. Therefore, today there is no mathematical models that rather adequately describe the nonstationary nonisothermal transport processes in electro-membrane systems based on the combined action of various types of convection, and this determines the relevance of this work.

Keywords: electromembrane systems, transfer of ions, mathematical models, gravity convection.

Увеличение потока противоионов соли за счет эффекта превышения значения электрического тока над предельным j_i lim (экзальтации) в электромембранных системах относительно невелико. Например, оно составляет около 0.2 j_i lim, когда поток OH^– ионов достигает значений, равных j_i lim. На практике приращение противоионов соли значительно выше [1, 2 - 3], следовательно, оно не может быть объяснено только эффектом экзальтации. Существенный вклад в сверхпредельный перенос противоионов соли должны вносить другие сопряженные эффекты. Именно речь идет о двух типах сопряженной конвекции, обеспечивающей дополнительное по сравнению с вынужденной конвекцией перемешивание раствора. Такое перемешивание вызвано локальными вихрями, возникающими в результате действия объемных сил, порожденных протеканием электрического тока [4]. Первый тип, сопряженной конвекции, гравитационная конвекция, развивается благодаря неравномерному распределению плотности раствора, которое является причиной возникновения объемной Архимедовой силы [5 - 7]. Заметим, что нередко в литературе можно встретить термины «естественная», «свободная», «термоконцентрационная» конвекция, используемые как синонимы гравитационной конвекции. Второй тип -электроконвекция, возникает вследствие действия электрического поля на пространственный электрический заряд в граничащем с мембраной обессоленном растворе [6].

В случае гравитационной конвекции возникновение объемной силы вызвано градиентами концентрации (концентрационная конвекция) и/или температуры (тепловая конвекция) [5-7]. В отличие от концентрационной, тепловая конвекция исследована достаточно подробно [5]. Это обусловлено, во-первых, относительно простым механизмом сил плавучести, во-вторых, более широким ее распространением [8, 9] и многочисленными техническими приложениями, в частности, для мониторинга окружающей среды [10, 11] и создания эффективных средств противопылевой [12] и противопожарной защиты [13]. В электрохимических системах силы плавучести индуцируются электродными процессами, и гравитационная конвекция представляет значительно более сложное явление. В тепловых системах только градиент температуры определяет изменение плотности жидкости и плотность сил плавучести. В электрохимических системах раствор содержит несколько сортов ионов, и градиент концентрации каждого из них влияет на плотность сил плавучести. Кроме того, в растворах электролитов, наряду с диффузионным существует и электромиграционный поток ионов, пропорциональный напряженности электрического поля. Поэтому число переменных, описывающих гравитационную конвекцию в электрохимических системах, возрастает, а сами уравнения становятся более сложными, чем в тепловых системах, в результате возникает сложная картина нелинейных взаимодействий концентрационных, гидродинамических и электрических полей. В некоторых случаях задачу о гравитационной конвекции в растворах электролитов можно свести к аналогичной проблеме для тепловой конвекции [5]. Однако, круг объектов, к которым применима такая аналогия, ограничен. Заметим, что оба типа гравитационной конвекции более вероятны в относительно концентрированных растворах, поскольку в них имеет место более сильный разогрев раствора и больший градиент концентраций [5, 7], обусловленные большей величиной предельной плотности электрического тока, в первом приближении пропорциональной концентрации раствора.

Явления, связанные с гравитационной конвекцией, можно разделить на два класса: свободную конвекцию и конвективную устойчивость. Свободная конвекция возникает в жидкости, если векторное произведение градиента плотности и вектора ускорения свободного падения удовлетворяет условию . Если же градиент плотности параллелен ускорению свободного падения , в жидкости возможно механическое равновесие. Однако это равновесие может оказаться неустойчивым, если плотность сил плавучести превысит некоторое критическое значение. При потере устойчивости амплитуда малых случайных возмущений начинает нарастать и в растворе возникают неравновесные диссипативные структуры, аналогичные ячейкам Бенара в неоднородно нагретой жидкости [14].

В случае отсутствия вынужденной конвекции (прокачивания раствора) известно [15], что, когда межфазная граница раствор/электрод (или мембрана) находится в вертикальном положении и градиент плотности раствора горизонтален, гравитационная конвекция возникает в беспороговом режиме, т.е. имеет место всегда и нарастает постепенно с увеличением тока/потенциала. Когда межфазная граница расположена горизонтально и плотность раствора, заключенного между двумя параллельными горизонтальными плоскостями, меняется по нормальной координате, возможны два случая. Если более легкий слой раствора (обедненный диффузионный слой) находится под рассматриваемой мембраной, а более тяжелый (обогащенный диффузионной слой) - над мембраной, конвекция вблизи этой мембраны не возникает. Если более легкий слой находится над мембраной, в развитии гравитационной конвекции имеется некоторый порог, определяемый значением числа Рэлея [16]:

где  − число Грасгофа;  − число Шмидта;  − изменение плотности раствора ρ между верхней и нижней частью слоя толщиной X, в котором происходит вариация плотности раствора; g – ускорение свободного падения; v − вязкость раствора, D − коэффициент диффузии электролита. Система стабильна, т. е. конвекция не возникает, если Ra<Ra_cr=1708. В этом случае характерное время, которое необходимо для диффузионной диссипации флуктуации плотности в небольшом объеме раствора, меньше, чем характерное время всплытия этого объема. Если Ra>Ra_cr, то объем с отрицательным градиентом плотности всплывает с ускорением, поскольку плотность внутри всплывающего объема увеличивается медленнее, чем в окружающем его растворе. Амплитуда небольшого возмущения в этом случае увеличивается со временем, и раствор между двумя плоскостями достигает состояния, характеризуемого периодической ячеистой вихревой структурой, где жидкость в двух соседних ячейках (ячейках Бенара) вращается в противоположных направлениях [5,7]. Из теории тепломассопереноса известно, что в случае «пустого» (не содержащего сепаратора) канала прямоугольного сечения гравитационная конвекция не подавляется вынужденной конвекцией, если соблюдается условие: Ri=Gr/Re²>1, где Ri − это число Ричардсона, а  − число Рейнольдса, V₀ – средняя линейная скорость вынужденного течения раствора.

Экспериментально роль гравитационной конвекции в увеличении массопереноса и уменьшении толщины обедненного диффузионного слоя при интенсивных токовых режимах была оценена с использованием вольтамперометрии и измерения парциальных чисел переноса ионов [17,18]. Её влияние на концентрационную поляризацию электромембранных систем изучали методами хронопотенциометрии и лазерной интерферометрии [19, 20]. Последний метод, а также микрофотосъемка с лазерной подсветкой [21, 22] были применены для визуализации конвективного движения жидкости. Параллельно структуру ячеек Бенара исследовали методом хронопотенциометрии [21, 22] с использованием Фурье - анализа полученных кривых. Фурье - анализ, а также вейвлет - анализ вольтамперных кривых позволил С.Ф. Тимашеву и сотрудникам [23] описать последовательность событий при развитии сопряженной конвекции у поверхности гомогенной катионообменной мембраны. В частности, было показано [23], что частота оборотов вихрей в стационарном состоянии электромембранной системы находится в области 0.1–0.4 Гц. Эти данные коррелируют с результатами Г.П. Весслера и соавторов [21], которые установили связь между характером колебаний потенциала на хронопотенциограммах и жизненным циклом вихрей у границы электрод/раствор. Авторы [21] показали также, что сопряженная конвекция может проявляться при Ra<Ra_cr=1708, и объяснили это воздействием кулоновских сил, т. е. электроконвекцией.

Цикл экспериментальных исследований массопереноса в электродиализных каналах обессоливания [14] позволил установить, что гравитационная конвекция является доминирующей, когда концентрация раствора достаточно высокая (порядка 0.05 М и больше), межмембранное расстояние составляет 5-7 мм, а скорость течения раствора не превышает 0.3 см/с. С разбавлением раствора, уменьшением межмембранного расстояния и увеличением скорости течения вклад гравитационной конвекции в массоперенос уменьшается, а электроконвекции – увеличивается. Дополнительные физические поля, в частности, магнитное поле,  могут усилить гравитационную конвекцию [24].

В соответствии со сложившимися к настоящему времени теоретическими представлениями, обзор которых можно найти в работах [7], основным механизмом развития электроконвекции в мембранных системах считается электроосмотическое скольжение второго рода (электроосмос II, согласно терминологии С.С. Духина и Н.А. Мищук [6], первыми изучавшими это явление). Электроосмос второго рода в мембранных системах возникает в результате взаимодействия электрического поля с индуцированным этим полем пространственным зарядом [25], появляющимся в обедненном диффузионном слое у межфазной границы. Поскольку протяженность пространственного заряда увеличивается с разбавлением раствора [26], следует ожидать, что с уменьшением концентрации соли вклад электроконвекции в сверхпредельный массоперенос будет расти.

Выяснено, что для возникновения электроконвекции в мембранной системе необходимы три условия [27]:

• наличие достаточно большого пространственного заряда;
• локализация заряда в растворе на достаточном удалении от поверхности мембраны;
• неравномерное распределение пространственного заряда.

Интенсивность электроконвекции должна зависеть не только от протяженности и плотности пространственного заряда, а также величины приложенного электрического поля, но также и от стоксовского радиуса ионов, формирующих область пространственного заряда. В самом деле, чем больше этот радиус, тем эффективнее жидкость должна вовлекаться в конвективное движение. С. Мун и сотрудники, по-видимому, первыми обратили внимание на это обстоятельство и сравнили вольтамперные характеристики мембраны CMX в растворах различных электролитов. Они действительно обнаружили, что с ростом стоксовского радиуса противоионов длина плато на вольтамперных характеристиках сокращается (чем короче плато, тем меньше напряжение, при котором начинается интенсивная сопряженная конвекция), а сопротивление электромембранной системы в сверхпредельных режимах уменьшается. Максимальная длина плато найдена в случае раствора HCl, поскольку перенос H⁺ ионов в растворе осуществляется не по гидродинамическому, а по эстафетному механизму [28]. Наличие электроосмоса II было подтверждено экспериментально у поверхности гранул ионообменной смолы, помещенных в разбавленный раствор между двумя поляризующими электродами. О наличии электроконвекции в электромембранных системах свидетельствует рост массопереноса в тех случаях, когда другие сопряженные эффекты концентрационной поляризации подавлены [17, 18].

Кроме того, в таких системах методом хронопотенциометрии зафиксировано появление высокочастотных осцилляций потенциала при условиях, предсказываемых теорией И. Рубинштейна [7].

Таким образом, анализ научной литературы показывает, что в теоретических исследованиях тепловой конвекции были получены выдающиеся результаты, в частности построено автомодельное решение, описывающее свободную конвекцию при больших числах Грасгофа [29]. Однако попытка распространить эти результаты на электрохимические системы сталкивается с серьезными проблемами, обусловленными прежде всего, многокомпонентной природой сил плавучести и существованием миграционного тока. Как показано в обзорной работе В.М. Волгина и Д.А. Давыдова [5], большинство из этих проблем не получило своего адекватного решения, но именно они в настоящее время привлекают к себе все большее внимание так как их решение открывает возможность исследования новых физико-химических явлений, не известных в тепловой конвекции.

Вместе с тем, вклад конвекции и ее учет при описании и анализе явлений переноса в электрохимических и в мембранных системах весьма важен. Во многих случаях при решении такого рода задач достаточно ограничиться использованием модели диффузионного слоя Нернста [26, 28]. Однако существует ряд задач, когда невозможно корректно описать процесс без непосредственного учета конвективного переноса. Речь идет о протяженных каналах в электрохимических мембранных системах, когда толщина диффузионного слоя меняется по длине, и особенно в тех случаях, когда диффузионные слои перекрываются, а понятие диффузионного слоя как погранслоя фактически теряет смысл [26, 30].

Другим интересным случаем, когда необходим учет гравитационной конвекции, является массоперенос в мембранной системе без вынужденной конвекции при протекании так называемого сверхпредельного тока. В этих условиях часто в системе появляется гидродинамическая неустойчивость, описанная в работах [1, 18, 23], в которых показано, что гравитационная конвекция разрушает диффузионный слой вблизи электрода/мембраны, способствуя резкому увеличению скорости подвода реагирующих веществ к их поверхности.

Проблема учета гравитационной конвекции важна также в теории хронопотенциометрических измерений, где гравитационная конвекция во многом определяет скорость массопереноса и существенно влияет на величину переходного времени. В.Г. Левич  в монографии дал решение задачи переноса ионов с учетом естественной конвекции, обусловленной неоднородным концентрационным полем, формирующимся в полубесконечном пространстве возле электрода при протекании постоянного тока. Он показал, что при достаточно большом удалении электродов друг от друга толщина стационарного диффузионного слоя обратно пропорциональна разности концентраций электролита в объеме и на поверхности электрода в степени 1/4. Современное состояние теории массопереноса в электродных системах с гравитационной конвекцией описано и проанализировано в обзоре [15]. В мембранных системах описание гравитационной конвекции с учетом изменения концентраций и джоулева разогрева проведено в работах В.А. Шапошника, Е.Н. Коржова и О.В. Григорчук (см., например, [30]). Однако в этих работах изучен только стационарный перенос и не рассматривается вынужденная конвекция и перенос тепла через мембрану, имеющие важное значение в ряде случаев.

Несовершенство модельных представлений делает невозможным адекватное описание процессов, протекающих в реальных электрохимических системах. Развитие этих модельных представлений, более корректное математическое описание сопряженной конвекции, и, в частности, гравитационной конвекции, позволило бы выявить условия, где этот эффект в наибольшей степени способствует интенсификации массопереноса, и открыло бы новые возможности совершенствования оборудования, предназначенного для очистки промышленных стоков и природных вод от антропогенных и естественных загрязнений.

Из проведенного анализа экспериментальных и теоретических работ можно сделать следующие выводы:

1. Для успешного применения электромембранных систем требуется глубокое понимание процессов массопереноса в этих системах. Отсюда возникает необходимость в построении адекватных математических моделей различных видов конвективных течений и исследовании основных закономерностей переноса в этих условиях.
2. Имеется большое количество работ, посвященных построению и исследованию математических моделей электрохимических систем с учетом гравитационной конвекции и электроконвекции. Однако в этих работах ограничиваются рассмотрением сравнительно простых математических моделей при различных упрощающих предположениях. В частности, в них изучен в основном стационарный перенос, не рассматривается вынужденная конвекция и перенос тепла через мембрану, имеющие важное значение в ряде случаев.
3. На сегодняшний день не существует математических моделей, достаточно адекватно описывающих нестационарные неизотермические процессы переноса в электромембранных системах с учетом совместного действия различных видов конвекции, что и определяет актуальность данной работы.

Литература

1. Певницкая М.В. Интенсификация массопереноса при электродиализе разбавленных растворов // Электрохимия. – 1992. – Т.28, №11. – С.1708-1715.
2. Zabolotsky V.I. On the role of gravitational convection in the transfer en-hancement of salt ions in the course of dilute solution electrodialysis / V.I. Zabolotsky, V.V. Nikonenko, N.D. Pismenskaya // J. Membr. Sci. – 1996. – V.119. – P.171-181.
3. Zabolotsky V.I. Coupled transport phenomena in overlimiting current electrodialysis / V.I. Zabolotsky, V.V. Nikonenko, N.D. Pismenskaya, M.Kh. Urtenov, E.V. Laktionov, H. Strathmann, M. Wessling, G.H. Koops // Sep. Pur. Tech. – 1998. – V.14. – P.255-267.
4. Тимашев С.Ф. Физико-химия мембранных процессов. – М.: Химия, 1988. – 240 с.
5. Волгин В.М. Естественно-конвективная неустойчивость электрохими-ческих систем / В.М. Волгин, А.Д. Давыдов // Электрохимия. – 2006. – Т.42, №6. – С.635-678.
6. Духин С.С. Электроосмос второго рода и неограниченный рост тока в смешанном монослое ионита / С.С. Духин, Н.А. Мищук, П.В. Тахистов // Коллоидн. журн. – 1989. – Т.51, № 3. – С.616-618.
7. Рубинштейн И. Экспериментальная проверка электроосмотического механизма формирования «запредельного» тока в системе с катионо-обменной электродиализной мембраной / И. Рубинштейн, Б. Зальцман, И. Прец, К. Линдер // Электрохимия. – 2002. – Т.38, № 8. – С.956-967.
8. Ambrosone L. Double-diffusive instability in free diffusing layers: a general formulation // Physica B: Condensed Matter. – 2000. – V.292, N.1-2. – P.136-152.
9. Anufriev A.P. The Boussinesq and anelastic liquid approximations for con-vection in the Earth’s core / A.P. Anufriev, C.A. Jones, A.M. Soward // Physics of The Earth and Planetary Interiors. – 2005. – V.152, N.3. – P.1-7.
10. Gertman I. The Dead Sea hydrography from 1992 to 2000 / I. Gertman, A. Hecht // J. Marine Systems. – 2002. – V.35, N.3-4. – P.169-181.
11. Simmons C.T. Mixed convection processes below a saline disposal basin / C.T. Simmons, K.A. Narayan // J. Hydrology. – 1997. – V.194, N.1-4. – P.263-285.
12. Nazaroff W.W. Mass-transport aspects of pollutant removal at indoor sur-faces / W.W. Nazaroff, G. R. Cass // Environment International. – 1989. – V.15, N.1-6. – P.567-584.
13. Wang H.Y. Three-dimensional modeling for prediction of wall fires with buoyancy-induced flow along a vertical rectangular channel / Wang H.Y., Joulain P. // Combustion and Flame. – 1996. – V.105, N.3. – P.391-406.
14. Григин А.П. Естественная конвекция в электрохимических системах / А.П. Григин А.Д. Давыдов // Электрохимия. – 1998. – Т.34, № 11. – С.1237-1263.
15. Григин А.П. Естественная конвекция в электрохимических системах / А.П. Григин А.Д. Давыдов // Электрохимия. – 1998. – Т.34, № 11. – С.1237-1263.
16. Volgin V.M. Simulation of ion transfer under conditions of natural con-vection by the finite difference method / V.M. Volgin, O.V. Volgina, D.A. Bograchev, A.D. Davydov // J. Electroanal. Chem. – 2003. V.546. – P.15-22.
17. Zabolotsky V.I. On the role of gravitational convection in the transfer en-hancement of salt ions in the course of dilute solution electrodialysis / V.I. Zabolotsky, V.V. Nikonenko, N.D. Pismenskaya // J. Membr. Sci. – 1996. – V.119. – P.171-181.
18. Zabolotsky V.I. Coupled transport phenomena in overlimiting current electrodialysis / V.I. Zabolotsky, V.V. Nikonenko, N.D. Pismenskaya, M.Kh. Urtenov, E.V. Laktionov, H. Strathmann, M. Wessling, G.H. Koops // Sep. Pur. Tech. – 1998. – V.14. – P.255-267.
19. Шапошник В.А. Термоконвективная неустойчивость в электродиализе / В.А. Шапошник, В.И. Васильева, Р.Б. Угрюмов, М.С. Кожевников // Электрохимия. – 2006. – Т.42, №5. – С.531-537.
20. Shaposhnik V.A. Concentration fields of solutions under electrodialysis with ion-exchange membranes / V.A. Shaposhnik, V.I. Vasil’eva, D.B. Praslov // J. Membr. Sci. – 1995. – V.101. – P.23-30.
21. Весслер Г.П. Оптическое и электрохимическое изучение диссипативных структур в растворах электролитов / Г.П. Весслер, В.С. Крылов, П. Шварц, Х. Линде // Электрохимия. – 1986. – Т.22, № 5. – С.623-628.
22. Lifson S. Flicker-noise of ion selective membranes and turbulent convection in the depleted layer / S. Lifson, B. Gavish, S. Reich // Biophys. Struct. Mech. – 1978. V.4, N 1. – P.53-65.
23. Вейвлет-анализ в приложении к исследованию природы запредельного тока в электрохимической системе с катионообменной мембраной / Е.Ю. Будников, А.В. Максимычев, А.В. Колюбин, В.Г. Меркин, С.Ф. Тимашев // Журнал физ. химии. – 1999. – Т.73. – С.198-213.
24. Голицын В.Ю. Электромассоперенос через ионселективные мембраны в условиях естественной конвекции в постоянном магнитном поле / В.Ю. Голицын, О.В. Бобрешова, С.Ф. Тимашев // Теор. основы хим. технол. – 1989. - Т.23, №3. – С.399-403.
25. Rubinstein I. Voltage against current curves of cation exchange mem-branes / I. Rubinstein, L. Shtilman // J. Chem. Soc. Faraday Trans. II. – 1979. – V.75. – P.231-246.
26. Заболоцкий В.И. Перенос ионов в мембранах / В.И. Заболоцкий, В.В. Никоненко. – М.: Наука, 1996. – 390 с.
27. Бабешко В.А. Взаимодействие гидродинамических и электрохимиче-ских полей в мембранных процессах / В.А. Бабешко, В.И. Заболоцкий, М.Х. Уртенов, Р.Р. Сеидов // Проблемы физико-математического моде-лирования. – 1998. – №1. – С.3.
28. Дамаскин Б.Б. Электрохимия / Б.Б. Дамаскин, О.А. Петрий, Г.А. Цир-лина. – М.: Химия, 2001. – 624 с.
29. Давыдов А.Д. Методы интенсификации некоторых электрохимических процессов / А.Д. Давыдов, Г.Р. Энгельгард // Электрохимия. – 1988. – Т.24, № 1. – С.3-17.
30. Коржов Е.И. Гидродинамические модели электромембранных систем: Дис. канд. физ.-мат. наук: 01.02.05 / – Воронеж, 1991 – 152 с.

References

1. Pevnickaja M.V. Intensifikacija massoperenosa pri jelektrodialize razbavlennyh rastvorov // Jelektrohimija. – 1992. – T.28, №11. – S.1708-1715.
2. Zabolotsky V.I. On the role of gravitational convection in the transfer en-hancement of salt ions in the course of dilute solution electrodialysis / V.I. Zabolotsky, V.V. Nikonenko, N.D. Pismenskaya // J. Membr. Sci. – 1996. – V.119. – P.171-181.
3. Zabolotsky V.I. Coupled transport phenomena in overlimiting current electrodialysis / V.I. Zabolotsky, V.V. Nikonenko, N.D. Pismenskaya, M.Kh. Urtenov, E.V. Laktionov, H. Strathmann, M. Wessling, G.H. Koops // Sep. Pur. Tech. – 1998. – V.14. – P.255-267.
4. Timashev S.F. Fiziko-himija membrannyh processov. – M.: Himija, 1988. – 240 s.
5. Volgin V.M. Estestvenno-konvektivnaja neustojchivost' jelektrohimi-cheskih sistem / V.M. Volgin, A.D. Davydov // Jelektrohimija. – 2006. – T.42, №6. – S.635-678.
6. Duhin S.S. Jelektroosmos vtorogo roda i neogranichennyj rost toka v smeshannom monosloe ionita / S.S. Duhin, N.A. Mishhuk, P.V. Tahistov // Kolloidn. zhurn. – 1989. – T.51, № 3. – S.616-618.
7. Rubinshtejn I. Jeksperimental'naja proverka jelektroosmoticheskogo mehanizma formirovanija «zapredel'nogo» toka v sisteme s kationo-obmennoj jelektrodializnoj membranoj / I. Rubinshtejn, B. Zal'cman, I. Prec, K. Linder // Jelektrohimija. – 2002. – T.38, № 8. – S.956-967.
8. Ambrosone L. Double-diffusive instability in free diffusing layers: a general formulation // Physica B: Condensed Matter. – 2000. – V.292, N.1-2. – P.136-152.
9. Anufriev A.P. The Boussinesq and anelastic liquid approximations for con-vection in the Earth’s core / A.P. Anufriev, C.A. Jones, A.M. Soward // Physics of The Earth and Planetary Interiors. – 2005. – V.152, N.3. – P.1-7.
10. Gertman I. The Dead Sea hydrography from 1992 to 2000 / I. Gertman, A. Hecht // J. Marine Systems. – 2002. – V.35, N.3-4. – P.169-181.
11. Simmons C.T. Mixed convection processes below a saline disposal basin / C.T. Simmons, K.A. Narayan // J. Hydrology. – 1997. – V.194, N.1-4. – P.263-285.
12. Nazaroff W.W. Mass-transport aspects of pollutant removal at indoor sur-faces / W.W. Nazaroff, G. R. Cass // Environment International. – 1989. – V.15, N.1-6. – P.567-584.
13. Wang H.Y. Three-dimensional modeling for prediction of wall fires with buoyancy-induced flow along a vertical rectangular channel / Wang H.Y., Joulain P. // Combustion and Flame. – 1996. – V.105, N.3. – P.391-406.
14. Grigin A.P. Estestvennaja konvekcija v jelektrohimicheskih sistemah / A.P. Grigin A.D. Davydov // Jelektrohimija. – 1998. – T.34, № 11. – S.1237-1263.
15. Grigin A.P. Estestvennaja konvekcija v jelektrohimicheskih sistemah / A.P. Grigin A.D. Davydov // Jelektrohimija. – 1998. – T.34, № 11. – S.1237-1263.
16. Volgin V.M. Simulation of ion transfer under conditions of natural con-vection by the finite difference method / V.M. Volgin, O.V. Volgina, D.A. Bograchev, A.D. Davydov // J. Electroanal. Chem. – 2003. V.546. – P.15-22.
17. Zabolotsky V.I. On the role of gravitational convection in the transfer en-hancement of salt ions in the course of dilute solution electrodialysis / V.I. Zabolotsky, V.V. Nikonenko, N.D. Pismenskaya // J. Membr. Sci. – 1996. – V.119. – P.171-181.
18. Zabolotsky V.I. Coupled transport phenomena in overlimiting current electrodialysis / V.I. Zabolotsky, V.V. Nikonenko, N.D. Pismenskaya, M.Kh. Urtenov, E.V. Laktionov, H. Strathmann, M. Wessling, G.H. Koops // Sep. Pur. Tech. – 1998. – V.14. – P.255-267.
19. Shaposhnik V.A. Termokonvektivnaja neustojchivost' v jelektrodialize / V.A. Shaposhnik, V.I. Vasil'eva, R.B. Ugrjumov, M.S. Kozhevnikov // Jelektrohimija. – 2006. – T.42, №5. – S.531-537.
20. Shaposhnik V.A. Concentration fields of solutions under electrodialysis with ion-exchange membranes / V.A. Shaposhnik, V.I. Vasil’eva, D.B. Praslov // J. Membr. Sci. – 1995. – V.101. – P.23-30.
21. Vessler G.P. Opticheskoe i jelektrohimicheskoe izuchenie dissipativnyh struktur v rastvorah jelektrolitov / G.P. Vessler, V.S. Krylov, P. Shvarc, H. Linde // Jelektrohimija. – 1986. – T.22, № 5. – S.623-628.
22. Lifson S. Flicker-noise of ion selective membranes and turbulent convection in the depleted layer / S. Lifson, B. Gavish, S. Reich // Biophys. Struct. Mech. – 1978. V.4, N 1. – P.53-65.
23. Vejvlet-analiz v prilozhenii k issledovaniju prirody zapredel'nogo toka v jelektrohimicheskoj sisteme s kationoobmennoj membranoj / E.Ju. Budnikov, A.V. Maksimychev, A.V. Koljubin, V.G. Merkin, S.F. Timashev // Zhurnal fiz. himii. – 1999. – T.73. – S.198-213.
24. Golicyn V.Ju. Jelektromassoperenos cherez ionselektivnye membrany v uslovijah estestvennoj konvekcii v postojannom magnitnom pole / V.Ju. Golicyn, O.V. Bobreshova, S.F. Timashev // Teor. osnovy him. tehnol. – 1989. - T.23, №3. – S.399-403.
25. Rubinstein I. Voltage against current curves of cation exchange mem-branes / I. Rubinstein, L. Shtilman // J. Chem. Soc. Faraday Trans. II. – 1979. – V.75. – P.231-246.
26. Zabolockij V.I. Perenos ionov v membranah / V.I. Zabolockij, V.V. Nikonenko. – M.: Nauka, 1996. – 390 s.
27. Babeshko V.A. Vzaimodejstvie gidrodinamicheskih i jelektrohimiche-skih polej v membrannyh processah / V.A. Babeshko, V.I. Zabolockij, M.H. Urtenov, R.R. Seidov // Problemy fiziko-matematicheskogo mode-lirovanija. – 1998. – №1. – S.3.
28. Damaskin B.B. Jelektrohimija / B.B. Damaskin, O.A. Petrij, G.A. Cir-lina. – M.: Himija, 2001. – 624 s.
29. Davydov A.D. Metody intensifikacii nekotoryh jelektrohimicheskih processov / A.D. Davydov, G.R. Jengel'gard // Jelektrohimija. – 1988. – T.24, № 1. – S.3-17.
30. Korzhov E.I. Gidrodinamicheskie modeli jelektromembrannyh sistem: Dis. kand. fiz.-mat. nauk: 01.02.05 / – Voronezh, 1991 – 152 s.