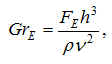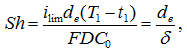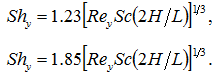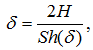INFLUENCE OF ELECTROCONVECTION ON TRANSPORT IN THE ELECTROMEMBRANE SYSTEMS FOR CLEANING MASSIVE GROUND AND SEWAGE WATER

Research article

Antoniady D.G.

Lavrentiev A.V.

DOI:

https://doi.org/10.18454/IRJ.2016.46.157

Issue: № 4 (46), 2016

Published:

2016/04/18

PDF

Антониади Д.Г.¹, Лаврентьев А.В.²

¹Доктор технических наук, профессор, ²ORCID: 0000-0002-4701-2020, докторант, Кубанский государственный технологический университет

ВЛИЯНИЕ ЭЛЕКТРОКОНВЕКЦИИ НА ПЕРЕНОС В ЭЛЕКТРОМЕМБРАННЫХ СИСТЕМАХ ОЧИСТКИ ПЛАСТОВЫХ И СТОЧНЫХ ВОД

Аннотация

Установлено, что электроконвекция приводит к существенному уменьшению эффективной толщины диффузионного слоя, так, например, при увеличении плотности тока в пять раз, толщина диффузионного слоя, монотонно убывая, падает практически в 5,5 раз.

Получена оценка: электроконвективные вихри имеют макроскопический размер, возмущения охватывают практически весь канал. Созданные модели, соответствующий математический аппарат и полученные фундаментальные результаты могут быть использованы в следующих практических целях: 1) при решении задач тепло- и массопереноса в экологии, в которых учитывается влияние электрического поля, вынужденной конвекции; 2) для совершенствования геометрических характеристик электромембранных модулей, в частности, конструкций электродиализных аппаратов; 3) для оптимизации условий эксплуатации существующих электромембранных систем очистки воды; 4) для выявления наиболее приемлемых параметров поверхности новых материалов, применяемых в мембранных нанотехнологиях.

Ключевые слова: электроконвекция, электромембранные системы очистки вод, математические модели.

Antoniady D.G.¹, Lavrentiev A.V.²

¹PhD in Engineering, professor, ²ORCID: 0000-0002-4701-2020, Doctoral student, Kuban State Technological University

INFLUENCE OF ELECTROCONVECTION ON TRANSPORT IN THE ELECTROMEMBRANE SYSTEMS FOR CLEANING MASSIVE GROUND AND SEWAGE WATER

Abstract

Established that electroconvection leads to a significant reduction in the effective thickness of the diffusion layer, for example, by increasing the current density in five times the thickness of the diffusion layer decreases monotonically decreases practically by 5.5 times.

An estimate is obtained: electric convective vortices have a macroscopic size, indignation cover almost the entire channel. The created models, the corresponding mathematical apparatus and obtained fundamental results can be used in the following practical reasons: 1) in solving of tasks of heat and mass transfer in the environment, which take into account the influence of the electric field, forced convection; 2) to improve geometrical characteristics of the electromembrane modules in particular constructions electrodialysis apparatus; 3) to optimize the of operating conditions existing electromembraneof water treatment systems; 4) to identify the most acceptable parameters of the surface new materials used in membrane nanotechnology.

Keywords: electroconvection, electromembrane systems of water treatment, mathematical models.

Далее рассмотрим явление электроконвекции, возникающей вследствие неоднородной электропроводности поверхности ионообменных мембран.

Неоднородность электрического поля, возникающая, вследствие неоднородной поверхности мембраны вызывает появление пространственной электрической (кулоновской) силы.

Эта электрическая сила воздействует на пространственный заряд, локализованный вблизи межфазной границы раствор/мембрана.

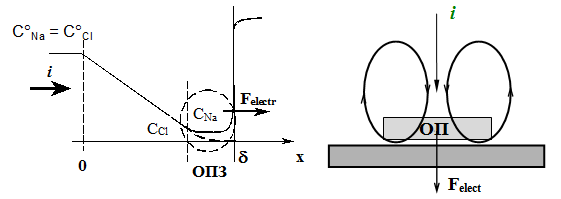
В результате воздействия электрической силы в некотором месте возникает избыточное давление, выталкивающее раствор. При своем движении выдавленная часть раствора встречает инерционное сопротивление невозмущенных слоев электролита и поверхности мембраны, что вызывает изменение направления движения жидкости, а именно удаление ее от поверхности мембраны, вследствие чего образуются два разнонаправленных вихря (рисунок 1). Эти вихри облегчают доставку ионов соли к межфазной границе и частично разрушают диффузионный слой, что приводит к уменьшению величины электрической силы.

Это в свою очередь вызывает уменьшение величины вихрей и соответственно влияния электроконвекции на массоперенос. Таким образом, с учетом диссипации энергии электроконвекция прекратится еще до того, как ток уменьшится до значения, равного предельному электродиффузионному току.

Рисунок 1 – Механизм возникновения электроконвекции

Ожидается, что электроконвекция должна приобретать большую роль с уменьшением концентрации раствора [2].

Исходя из этих рассуждений, получаем, что необходимым условием возникновения электроконвекции являются:

а) электрическая неоднородность поверхности мембраны. Эта неоднородность обусловлена структурой образования мембраны. Визуально поверхность мембрана представлена на рисунке 2. Армированная сетка полиэтилена помещается в ионообменную смолу. Под действием температуры и давления данное соединение раскатывается, в результате чего образуется мембрана. Как видно из указанного рисунка поверхность мембраны электрически является неоднородной.

Рисунок 2 – (а) Фотография поверхности ионообменной мембраны МА-41, полученной электронным микроскопом в Европейском Институте Мембран (г.Монпелье Франция) [1]. (б) Увеличенное изображение участка поверхности мембраны, где видно, что смола прорывает полиэтилен

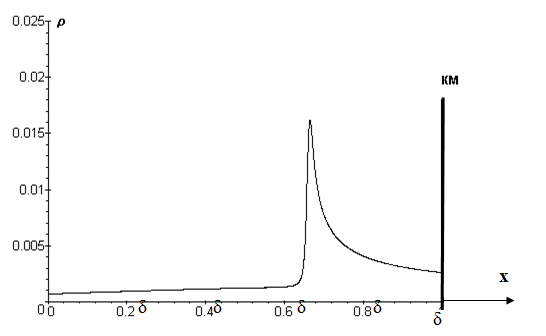
Рисунок 3 – Распределение плотности электрического заряда в диффузионном слое из расчета одномерной модели (КМ – катионоообменная мембрана)

Смола прорывает полиэтилен. И с учетом того, что смола пропускает электрический ток, а полиэтилен является изолятором и не пропускает электрический ток, то можно утверждать, что мембрана имеет электрически неоднородную поверхность. Наличие этой неоднородности можно считать, таким образом, установленной экспериментально;

б) наличие пространственного заряда, локализованного на некотором расстоянии от межфазной границы. Численный и асимптотический анализ модельных краевых задач для указанной выше системы уравнений Нернста-Планка и Пуассона в одномерном случае показывает наличие пространственного заряда, локализованного на некотором расстоянии от межфазной границы (рисунок 3) [3, 4].

в) величина электрической силы должна быть достаточно большой. Электрическое число Грасгофа

достигает величин уже при скачке потенциалов 3–4 В на парную камеру;

г) при моделировании электроконвекции кулоновская сила, как массовая сила, входит в правую часть системы уравнений Навье-Стокса.

Расчеты вихрей, полученные в результате решения краевой задачи для этой системы с соответствующими граничными условиями для указанных выше чисел Грасгофа и сил специального вида, показывают, что вихри захватывают большую часть канала обессоливания [3, 5];

д) можно ожидать, что электроконвекция вызывает уменьшение эффективной толщины диффузионного слоя, что в свою очередь быстро приводит к уменьшению величины электрической силы и соответственно влияния электроконвекции и в результате возникает некоторое равновесие, которому соответствует определенная эффективная толщина диффузионного слоя, которую будем называть «равновесной».

Для составления математической модели необходимо установить связь между числовыми характеристиками вихрей и массопереносом и на основе, которой составить уравнение для «равновесной» толщины диффузионного слоя, а также решить это уравнение.

Независимо от природы образования, вихри в канале обессоливания электродиализатора приводят к интенсификации массопереноса, т.е. к дополнительному массопереносу по сравнению с безвихревым случаем.

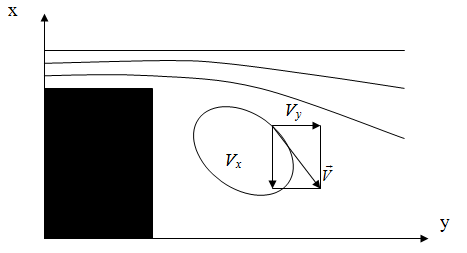
Как видно из рисунка 4, дополнительный подвод ионов соли происходит за счет составляющей скорости V_x, которая в безвихревом течении равна нулю.

Рисунок 4 – Схема к выводу характеристики массопереноса в каналах с препятствием

Чтобы установить связь между числовыми характеристиками вихря и массопереносом, проанализируем характеристики массопереноса в каналах без препятствия и с препятствием.

Характеристики массопереноса в каналах без препятствий

Гидродинамические свойства безвихревого течения характеризуются числом Рейнольдса

которое выражает отношение сил инерции к силам вязкости.

Отношение сил вязкости к силам диффузии выражается числом Шмидта:

Скорость массопереноса определяется числом Шервуда, которое с учетом связи предельной плотности тока с толщиной диффузионного слоя δ может быть выражено в двух формах:

где T₁ и t₁ – соответственно эффективное число переноса противоионов в мембране и в растворе; d_e – характерный размер, который для каналов ширины H равен d_e=2H.

Для не слишком длинных (L) и гладких каналов толщина диффузионного слоя может быть рассчитана по формуле [3]

Следовательно, формулы для локального и интегрального чисел Шервуда принимают, соответственно, вид:

Характеристики массопереноса в каналах с препятствиями.

Для каналов с препятствиями V_x≠ 0, и поэтому естественно наряду с числом ввести в рассмотрение еще одно число Рейнольдса:

где d – "диаметр" вихря. Добавочный массоперенос можно теперь описать по аналогии с этой формулой еще одним числом Шервуда:

а общий массоперенос – общим числом Шервуда:

Заметим, что число Шервуда, вследствие формулы (6.1), зависит от "диаметра" вихря d, т.е.

Коэффициенты k₁, n₁ в этой формуле берем такие же, как для ламинарного течения, т.е. k₁=1.23, n₁=0.33, n₂ полагаем равным 1, а k₂ рассчитываем, используя экспериментальные данные по массопереносу в системах с спейсерами. При этом размер вихря d полагается равным высоте препятствия. В таблице 1 представлены экспериментальные данные, полученные на кафедре физической химии КубГУ.

Таблица 1 – Зависимость Sh от Re

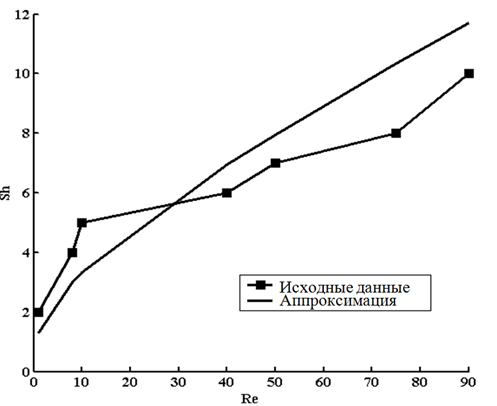
Ниже на рисунке 5 приведен график, построенный по исходным данным, и график аппроксимирующий их функции.

Рисунок 5 – Графики исходных данных и аппроксимирующей их функции. Расчеты производятся при следующих значениях: k₁ = 1,23; n₁ = 0,33; k₂ = 0,069661; n₂ = 1.

«Диаметр» вихря d зависит от величины массовой силы , которая, в свою очередь, зависит от безразмерной толщины диффузионного слоя δ, т.е. и таким образом число Шервуда также зависит от δ, т.е. .

С использованием числа Шервуда Sh, толщина диффузионного слоя находится по формуле

откуда получаем следующее уравнение для толщины диффузионного слоя δ:

Вид полученного выше уравнения определяется зависимостью числа Шервуда Sh от толщины диффузионного слоя d. Нахождение этой зависимости представляет собой нетривиальную задачу математического моделирования решенную в [3]. С учетом полученной в [3] зависимости для толщины диффузионного слоя d получается квадратное уравнение, при помощи которого и вычисляется данная величина.

Зная δ и используя конечно-разностные методы можно расчитать все характеристики массопереноса.

Приведем некоторые результаты численного анализа [6].

На рисунках 6 и 7 приведены линии тока жидкости.

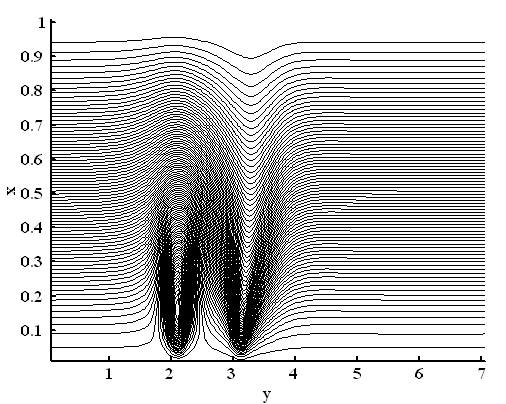
Рисунок 6 – Функция тока жидкости

На рисунке 6 раствор прокачивается слева направо. В области от 2.1 до 2.3 по у и от 0 до 0.5 по х образуется вихрь, закручивающийся по часовой стрелке. В области от 3.1 до 3.3 по у и от 0 до 0.5 по х вихрь не образуется, но происходит сильное искривление течения.

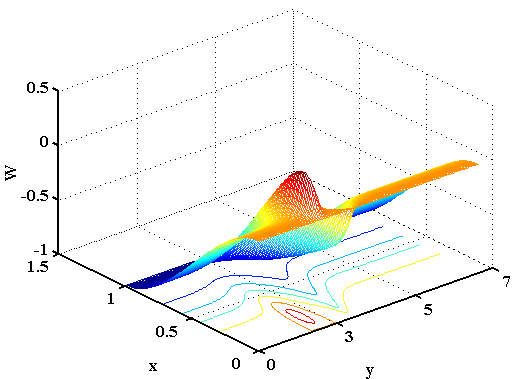
На рисунке 7 представлен график функции тока жидкости, на котором видны числовые значения функции тока. В области от 2.1 до 2.3 по у и от 0 до 0.5 по х, где образуется вихрь, который закручивается по часовой стрелке, функция тока принимает положительные значения, а в области от 3.1 до 3.3 по у и от 0 до 0.5 по х принимает отрицательные значения.

Рисунок 7 – Функция тока жидкости

На рисунке 8 приведены зависимость толщины диффузионного слоя δ (см) от плотности тока i⁽^d⁾, причем расчеты проведены при следующих данных: см²/с, моль/см³, F=96484.56 Кл/моль, H=5 см, v=0.01 см²/с, u=10 см/с, Re_y=10.

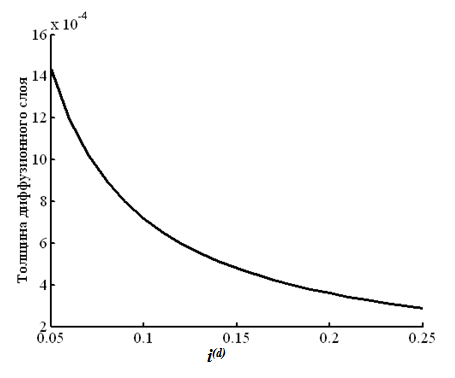
Из рисунка видно, что при увеличении плотности тока в пять раз, толщина диффузионного слоя, монотонно убывая, падает практически в 5,5 раз.

Рисунок 8 – Поведение толщины диффузионного слоя δ (см) в зависимости от плотности тока i⁽^d⁾(А/см² )

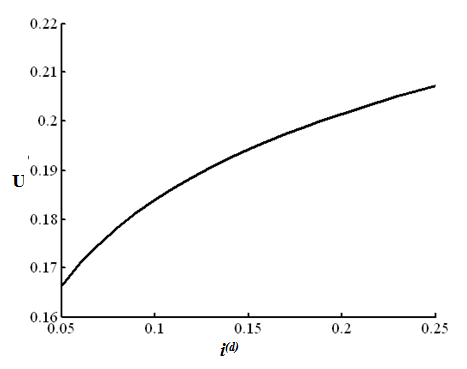
Рисунок 9 – Поведение вольтамперной характеристики

На рисунке 9 приведена вольтамперная характеристика, рассчитанная с использованием математической модели. Видно, что с увеличением плотности тока i⁽^d⁾ от 0.05 до 0.25 А/см², падение потенциала также увеличивается, монотонно возрастая, причем она увеличивается примерно в 2 раза при увеличении плотности тока в 5 раз. Заметим, что на кривой отсутствует выраженное «плато», возникающее в моделях, не учитывающих явление электроконвекции.

Анализируя, полученные выше результаты можно сделать выводы:

Установлено, что электроконвекция приводит к существенному уменьшению эффективной толщины диффузионного слоя, так, например, при увеличении плотности тока в пять раз, толщина диффузионного слоя, монотонно убывая, падает практически в 5,5 раз.
Получена оценка: электроконвективные вихри имеют макроскопический размер, возмущения охватывают практически весь канал.
Созданные модели, соответствующий математический аппарат и полученные фундаментальные результаты могут быть использованы в следующих практических целях: 1) при решении задач тепло- и массопереноса в экологии, в которых учитывается влияние электрического поля, вынужденной конвекции; 2) для совершенствования геометрических характеристик электромембранных модулей, в частности, конструкций электродиализных аппаратов; 3) для оптимизации условий эксплуатации существующих электромембранных систем очистки воды; 4) для выявления наиболее приемлемых параметров поверхности новых материалов, применяемых в мембранных нанотехнологиях.

Литература

Цай Б.Н., Бондаренко Т.Т., Бахтыбаев Н.Б. О дилатансии горных пород при их разрушении // Вестник КазНТУ, 2008. – № 5 – С. 21-36.
Лаврентьев А.В. Антониади Д.Г. Влияние сопряженной конвекции на процесс электродиализной очистки сточных вод. Научно-технический журнал «Защита окружающей среды в нефтегазовом комплексе». 2015. № 12. – С. 38-44.
Лаврентьев А.В., Письменский А.В., Уртенов М.Х. Математическое моделирование переноса в электромембранных системах с учётом конвективных течений (монография). – Краснодар: Изд-во КубГУ, 2006. – 146 с.
Лаврентьев А.В., Сеидова Н.М., Уртенов М.Х. Математические модели некоторых сопряжённых эффектов в электромембранных системах. – Краснодар: Издательство КубГТУ, 2005.
Антониади Д.Г., Лаврентьев А.В. и др. Математическое моделирование электро-мембранной очистки пластовых и сточных вод. Труды IV Международной научно-практической конференции «Достижения и перспективы естественных и технических наук». Направление «Охрана окружающей среды и экология». – Ставрополь, 2014. – С.
Лаврентьев А.В. Описание нестационарного неизотермического процесса переноса ионов при электромембранной очистке воды. Материалы ХI Международной научно-практической конференции «Науки о земле на современном этапе». – М.: Из-дательство «Спутник+», 2014. – С. 68-76.

References

Caj B.N., Bondarenko T.T., Bahtybaev N.B. O dilatansii gornyh porod pri ih razrushenii // Vestnik KazNTU, 2008. – № 5 – S. 21-36.
Lavrent'ev A.V. Antoniadi D.G. Vlijanie soprjazhennoj konvekcii na process jelektrodializnoj ochistki stochnyh vod. Nauchno-tehnicheskij zhurnal «Zashhita okruzhajushhej sredy v neftegazovom komplekse». 2015. № 12. – S. 38-44.
Lavrent'ev A.V., Pis'menskij A.V., Urtenov M.H. Matematicheskoe modelirovanie perenosa v jelektromembrannyh sistemah s uchjotom konvektivnyh techenij (monografija). – Krasnodar: Izd-vo KubGU, 2006. – 146 s.
Lavrent'ev A.V., Seidova N.M., Urtenov M.H. Matematicheskie modeli nekotoryh soprjazhjonnyh jeffektov v jelektromembrannyh sistemah. – Krasnodar: Izdatel'stvo KubGTU, 2005.
Antoniadi D.G., Lavrent'ev A.V. i dr. Matematicheskoe modelirovanie jelektro-membrannoj ochistki plastovyh i stochnyh vod. Trudy IV Mezhdunarodnoj nauchno-prakticheskoj konferencii «Dostizhenija i perspektivy estestvennyh i tehnicheskih nauk». Napravlenie «Ohrana okruzhajushhej sredy i jekologija». – Stavropol', 2014. – S.
Lavrent'ev A.V. Opisanie nestacionarnogo neizotermicheskogo processa perenosa ionov pri jelektromembrannoj ochistke vody. Materialy HI Mezhdunarodnoj nauchno-prakticheskoj konferencii «Nauki o zemle na sovremennom jetape». – M.: Iz-datel'stvo «Sputnik+», 2014. – S. 68-76.