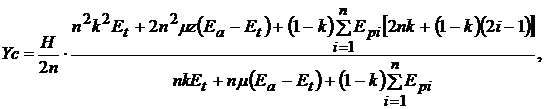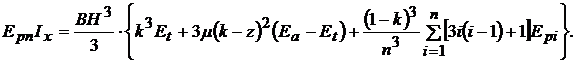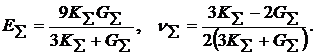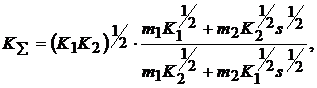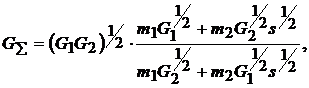EVALUATION OF BEARING CAPACITY OF REINFORCED BENDING ELEMENTS MADE OF POLYMER COMPOSITE MATERIAL WITH NONLINEAR ELASTIC HETEROGENEOUS MATRIX

Вержбовский Г.Б.¹, Жданов А.Г.²

¹ ORCID: 0000-0002-8412-2675, Доктор технических наук, ² Магистрант, Ростовский государственный строительный университет

ОЦЕНКА НЕСУЩЕЙ СПОСОБНОСТИ АРМИРОВАННЫХ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ, ВЫПОЛНЕННЫХ ИЗ ПОЛИМЕРНОГО КОМПОЗИТНОГО МАТЕРИАЛА С НЕЛИНЕЙНО УПРУГОЙ РАЗНОМОДУЛЬНОЙ МАТРИЦЕЙ

Аннотация

Предложена инженерная методика оценки несущей способности изгибаемых элементов несущих строительных конструкций с армированием и без, выполненных из полимерных композитных материалов. Представлены результаты численного эксперимента по оценке влияния на жесткость элемента нелинейной упругости и разномодульности матрицы композита.

Ключевые слова: полимерный композит, порошковый наполнитель, нелинейная упругость, арматура, численный эксперимент.

 

Verzhbovskiy G.B.¹, Zhdanov A.G.²

¹ ORCID: 0000-0002-1825-0097, PhD in Engineering, ² Undergraduate, Rostov State University of Civil Engineering

EVALUATION OF BEARING CAPACITY OF REINFORCED BENDING ELEMENTS MADE OF POLYMER COMPOSITE MATERIAL WITH NONLINEAR ELASTIC HETEROGENEOUS MATRIX

Abstract

Engineering methods of estimation of bearing capacity of flexible bearing elements of building structures with and without reinforcement, made of polymer composite materials is proposed. The results of a numerical experiment to assess the influence on the stiffness element for heterogeneous nonlinear elasticity matrix of the composite are presents.

Keywords: polymer composites, powdered filler, nonlinear elasticity, reinforcing bar, numerical experiment.

Появление в последнее время новых искусственных строительных материалов, особое место среди которых занимают порошковые композиты с полимерными матрицами, требует всестороннего изучения их физико-механических характеристик и корректного прогнозирования поведения изделий из них. Такие полимеры как полипропилен и полиэтилен, используемые в качестве связующего композитного материала (КМ), обладают рядом специфических свойств. Прежде всего – это различные модули упругости материала, учитываемые при его работе на сжатие, растяжение и изгиб, а также нелинейно упругая зависимость между напряжениями и деформациями сжатой зоны [1, 2].

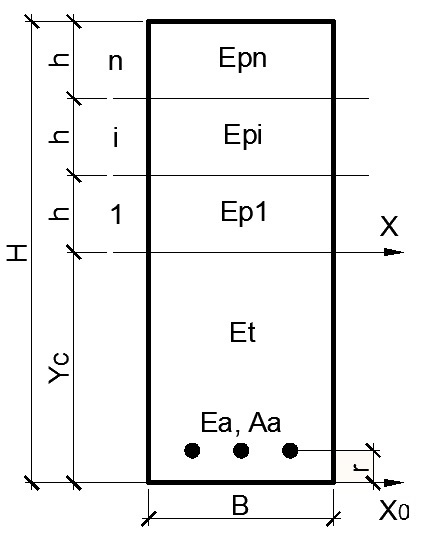
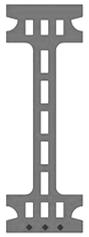
Рассмотрим сплошной прямоугольный выполненный из КМ с полипропиленовой матрицей и наполнителем из древесной муки изгибаемый элемент, показанный на рисунке 1.

Рис. 1. Расчетная модель изгибаемого элемента

Предположим, что сжатая зона располагается выше нейтральной плоскости. Обозначим модули упругости композиционного материала при растяжении и сжатии, а также модуль упругости арматуры как E_t, E_p и E_a соответственно. Принимая во внимание сведения, представленные в работе [1], будем считать, что при уровне напряжений в материале, не превосходящем его длительную прочность E_t=const, а E_p изменяется по нелинейному закону, описываемому алгебраическим полиномом третьей степени. Ставится задача определения приведенных геометрических характеристик элемента.

В рассматриваемом случае для получения результатов с заданной точностью разобьем сжатую зону поперечного сечения элемента на n участков одинаковой высоты с нумерацией, начинающейся от нейтральной плоскости. На верхней границе каждого участка определяется величина нормальных напряжений, возникающих в элементе от внешних воздействий. Далее по полученным значениям σ отыскиваются значения E_pi, вычисляются геометрические характеристики сечения и производится уточнение положения нейтральной плоскости. Итерационный процесс сходится для всех реальных сочетаний материалов матрицы и наполнителя.

Запишем выражения, определяющие положение нейтральной плоскости (1) и величину приведенного к E_pn центрального осевого момента инерции (2),:

         (1)

   (2)

В последних формулах с целью сокращения письма использованы следующие подстановки:

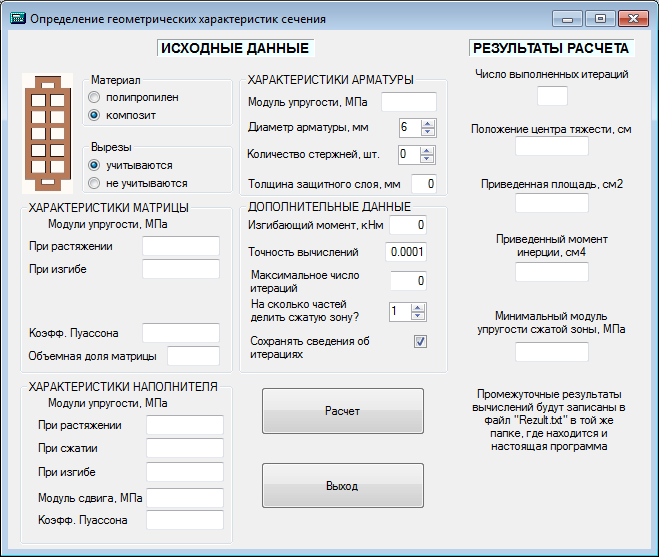
Для поперечных сечений иной формы можно записать аналогичные выражения, однако они будут значительно сложнее и потребуют применения вычислительной техники. В связи с этим составлена программа для персонального компьютера, при помощи которой был выполнен численный эксперимент над несколькими видами изгибаемых элементов, выполненных из полимерного композитного материала. Рисунок 2 представляет стартовое окно программы для изделия, являющегося частью универсального набора элементов, предназначенного для замены деловой древесины в легкокаркасных и брусчатых малоэтажных зданиях. На указанный набор подана заявка на изобретение, в настоящее время проходящая экспертизу.

Рис. 2. Стартовое окно программы

Особенностью программы является ее универсальность, позволяющая оценивать несущую способность как сплошных прямоугольных сечений, так и изделий с вырезами, выполненных из композитного материала, либо только из полимера.

Первый этап численного эксперимента заключался в определении оптимального числа частей, на которые необходимо разделить сжатую зону изгибаемого элемента с поперечным сечением в виде сплошного прямоугольника, полностью выполненного из полипропилена. При этом приемлемым для инженерных расчетов результатом считалось совпадение значений Y_c двух последовательных вычислений с точностью до целых миллиметров. Установлено, что разбиение сжатой зоны на пять частей оказывается достаточным, а решение сходится в среднем за семь итераций.

На следующем этапе оценивалось влияние учета вырезов в изделии на точность результатов. Для элемента, полностью выполненного из полипропилена, можно по-прежнему ограничиться разбиением сжатой зоны на пять частей. С учетом того, что доля матрицы в композитном материале составляет обычно не более 30%, было принято решение о сохранении подобного разбиения и при рассмотрении задачи об изгибе изделия из композита.

Физико-механические характеристики современных искусственных материалов зависят от многих факторов, в том числе и от свойств их составляющих. Безусловно, точные значения модулей упругости, пределов прочности и т.п. композитных материалов можно установить после проведения физических экспериментов. Тем не менее, существуют методики, позволяющие оценить эти характеристики еще на этапе создания материала. Одна из таких методик, учитывающая положения закона Гука и правило смеси, была предложена в [3].

Согласно ей, модуль упругости и коэффициент Пуассона КМ находятся по формулам:

                                                       (3)

Входящие в правые части выражений (3) объемные модули материала представляются в виде

                                   (4)

                            (5)

причем m₁ и m₂ – объемные доли матрицы и наполнителя соответственно (m₁ + m₂ = 1), а s=E₁/E₂.

Зависимости (3) – (5) использованы в компьютерной программе для определения несущей способности изделий из композитных материалов. В результате численного эксперимента установлена несущая способность показанного на рисунке 2 элемента без армирования, принятая за базовую при дальнейших расчетах.

Заключительная часть эксперимента была посвящена изучению влияния армирования на жесткость изделия. Конструктивные особенности его поперечного сечения ограничили верхний предел общей площади используемой арматуры одним процентом от площади нетто элемента. Предполагалось применение композитной арматуры периодического профиля, которую возможно вводить в расплав КМ во время экструзионного производства изделий. Расчеты показали, что таким образом жесткость можно увеличить на 6%.

Существенно лучшие результаты показал расчет балки двутаврового поперечного сечения (рисунок 3), возрастание жесткости которого в полтора раза произошло при проценте армирования 3%.

Численный эксперимент над армированными изгибаемыми элементами, выполненными из композитных материалов, доказал необходимость учета особенностей поведения матрицы для корректной оценки их прочностных и жесткостных свойств. Армирование несущих конструкций из полимерных КМ приводит к достаточно существенному возрастанию их несущей способности и способствует массовому внедрению новых материалов в малоэтажное домостроение. Предложенная инженерная методика является универсальной и может быть использована для расчета других аналогичных изделий.

 Рис. 3. Армированная балка перекрытия из композитного материала

Литература

1. Пилиповский П.И., Ярцев И.К. Полипропилен. Л: Химия, 1967, 316 с.
2. Ochsner Andreas and others. Mechanics and Properties of Composed Materials and Structures. Berlin Heidelberg: Springer-Verlag, - 2012. - 195 p.
3. Вержбовский Г. Б. Прогнозирование характеристик композитных материалов на основе свойств составляющих их частей // Науковедение. - 2014. - №7. - С. 909-914.

References

1. Pilipovskij P.I., Jarcev I.K. Polipropilen. L: Himija, 1967, 316 s.
2. Ochsner Andreas and others. Mechanics and Properties of Composed Materials and Structures. Berlin Heidelberg: Springer-Verlag, - 2012. - 195 p.
3. Verzhbovskiy G. B. Prognozirovanie harakteristik kompozitnyh materialov na osnove svojstv sostavljajushhih ih chastej // Naukovedenie. - 2014. - №7. - S. 909-914.