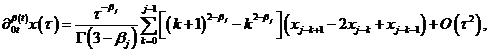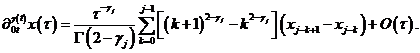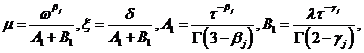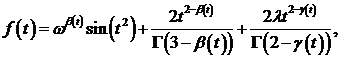CONCERNING ONE FINITE DIFFERENCE SCHEMES FOR MATHEMATICAL MODELS HEREDITARITY LINEAR OSCILLATOR

Паровик Р.И.

ORCID: 0000-0002-1576-1860, кандидат физико-математических наук, доцент, Камчатский государственный университет имени Витуса Беринга, ²Институт космофизических исследований и распространения радиоволн ДВО РАН

ОБ ОДНОЙ КОНЕЧНО-РАЗНОСТНОЙ СХЕМЕ ДЛЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ НЕЛИНЕЙНОГО ЭРЕДИТАРНОГО ОСЦИЛЛЯТОРА

Аннотация

В статье рассматривается обобщение нелинейного осциллятора на случай учета свойства эредитарности или памяти. В этом случае модельное уравнение осциллятора приводится к уравнению с производными дробных порядков. Далее ставиться задача Коши, которая решается с помощью явной конечно-разностной схемы. Исследованы вопросы аппроксимации, устойчивости и сходимости этой конечно-разностной схемы к точному решению.

Ключевые слова: эредитарность, численные методы, нелинейный осциллятор.

Parovik R.I.

ORCID: 0000-0002-1576-1860, PhD in Physics and Mathematics, Associate professor, Vitus Bering Kamchatka State University, Institute of Cosmophysical Research and Radio Wave Propagation FEB RAS

CONCERNING ONE FINITE DIFFERENCE SCHEMES FOR MATHEMATICAL MODELS HEREDITARITY LINEAR OSCILLATOR

Abstract

The article discusses the generalization of nonlinear oscillator to the case of properties hereditarity or memory. In this case, the oscillator model of the equation is an equation with derivatives of fractional order. Then put the Cauchy problem, which is solved by the explicit finite-difference scheme. The problems of approximation, stability and convergence of the finite-difference scheme to the exact solution.

Keywords: hereditarity, numerical methods, nonlinear oscillator.

Введение

В настоящее время развивается новое научное направление в нелинейной динамике – дробная или фрактальная динамика [1]. Дробная динамика характеризует нелокальные по времени динамические процессы с памятью или эредитарностью. В такой динамической системе ее состояния зависят от предыстории. С точки зрения математики, такую систему можно описать с помощью интегро-дифференциальных уравнений, как в работе Вито Вольтерры по исследованию эредитарного осциллятора [2]. Если интегральный оператор обладает степенным ядром, то с помощью некоторых преобразований интегро-дифференциальные уравнения динамической системы переходят в уравнения с дробными производными [3-5]. Поэтому такую динамику называют дробной или фрактальной. Мы же будем назвать ее эредитарной, а динамическими процессы – эредитарными как в работах [2,3,6].

В настоящей работе мы рассмотрим обобщение нелинейного осциллятора с трением и внешней силой, который описывает эредитарный колебательный процесс. Это обобщение заключается во введении в модельное уравнение производных дробного порядка. Далее с помощью явной конечно-разностной схемы находится его решение [7,8]. В работе также рассматриваются вопросы аппроксимации, устойчивости и сходимости конечно-разностной схемы.

Постановка задачи

Рассмотрим следующую задачу Коши:

,               (1)

,

где 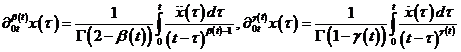 – операторы производных дробных переменных порядков  и ,  – гамма-функция Эйлера,  – заданные параметры,  – внешнее воздействие,  – время процесса.

Отметим, что задача (1) в случае, когда  переходит в задачу для классического нелинейного осциллятора с трением и внешней силой.  Заметим, что дробные параметры  и   представляют собой ограниченные функции.

Методика решения

Задача (1) в общем случае не имеет точного решения. Поэтому мы будем искать решение с помощью теории разностных схем [9]. Построим явную конечно-разностную схему. Разобьем отрезок  на  равных частей с постоянным шагом . Тогда  – численное сеточное решение, аппроксимирующее решение  дифференциальной задачи (1). Операторы производных дробного порядка аппроксимируются следующим образом [10]:

               (2)

Подставляя соотношения (2) в уравнение (1), после некоторых преобразований приходим к следующей явной конечно-разностной схеме:

                                                                       (3)

Заметим, что схема (3) имеет во внутренних точках второй порядок аппроксимации, однако за счет аппроксимации в граничных точках, порядок понижается до единицы. Это можно устранить, аппроксимируя значения в граничных точках специальным образом, например, введением фиктивного узла.

В рамках этой работы нас не будет интересовать улучшение схемы (3). Исследуем схему (3) на устойчивость и сходимость. Для этого проведем численный эксперимент. Можно показать, что функция  является решением следующей задачи Коши:

,

                               (4)

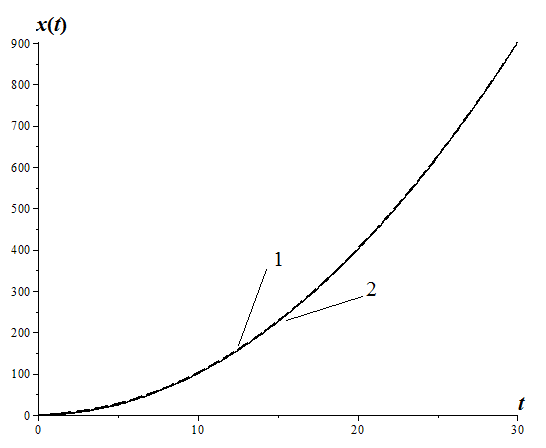
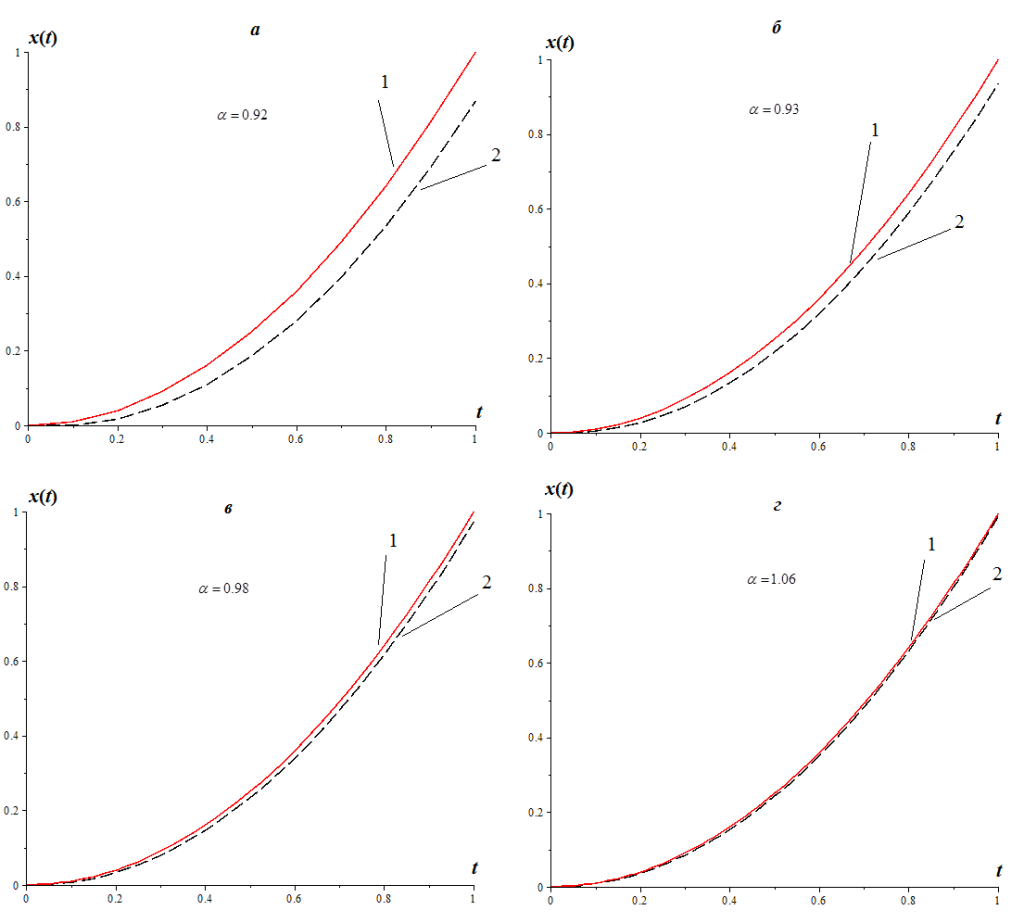
На рис.1 приведены расчетные кривые: кривая 1 – точное решение, кривая 2 – численное решение задачи (4), полученное по схеме (3) с учетом, что ,

   

Рис.1 -  Расчетные кривые: 1- точное решение, 2 – численное решение, полученное по схеме (3)

На рис.1 видно, что численное решение задачи (4) хорошо аппроксимирует точное. Рассмотрим вопросы устойчивости и сходимости схемы (3).  Напомним, что конечно-разностная схема будет являться устойчивой по правой части или по начальным данным, если их малое возмущение приводит к малому возмущению решения. Это определение можно записать так:

,                                   (5)

где   – возмущенное решение задачи,  – невозмущенное решение задачи,  – возмущение задачи,  – константа, которая не зависит от сеточных параметров.

Проведем численный эксперимент. Добавим сначала возмущение   в правую часть задачи (4) и решим возмущенную задачу с помощью схемы (3) при различных значениях узлов расчетной сетки.  Результаты приведены табл. 1.

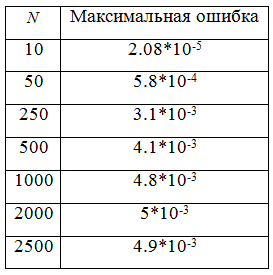
Таблица 1. Устойчивость по правой части

Из табл.1 можно сделать вывод, что при выбранных значениях управляющих параметров задачи (4) и возмущении , явная конечно-разностная схема (3) устойчива по правой части, так как значения максимальной по абсолютной величине ошибка между численным и точным решениями соизмеримы  с максимальным значением возмущения .

Можно также заметить, что при увеличении количества узлов  в расчетной сетке, максимальная ошибка составляет величину , что удовлетворяет неравенству (5) .

Аналогично проведем численный эксперимент для проверки устойчивости по начальным данным конечно-разностной схемы (3). Введем в начальные данные возмущение вида:   и найдем решение возмущенной задачи с помощью схемы (3). Результаты эксперимента приведены в следующей табл. 2.

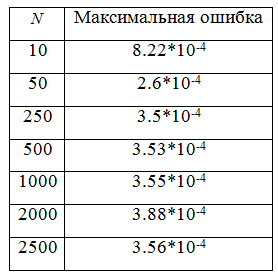
Таблица 2. Устойчивость по начальным данным

 

Из табл. 2 можно сделать вывод, что значения максимальной ошибки при увеличении количества узлов  расчетной сетки соизмеримы с возмущением . Поэтому в этом случае схема (3) устойчива по начальным данным.

Сходимость схемы (3) для задачи Коши проведем покажем с помощью численного эксперимента. Выберем значения управляющих параметров следующими:  и   Найдем максимальную по абсолютной величине ошибку между численным и точным решениями в зависимости от шага , а так же рассчитаем экспериментальный порядок сходимости численного решения к точному. Результаты эксперимента приведены в следующей табл. 3.

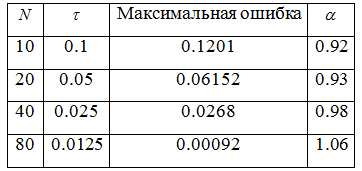
Таблица 3. Сходимость схемы (3) к точному решению

Из табл.3. можно сделать вывод, что при уменьшении шага   расчетной сетки максимальная ошибка уменьшается, а значения экспериментального порядка сходимости   близки к единице. Поэтому мы можем сделать вывод, что схема (3) сходится к точному решению с первым порядком (рис. 2).

Рис. 2. Расчетные кривые: 1- точное решение, 2- численное решение

Заключение

Как показали численные эксперименты, конечно-разностная схема (3) является устойчивой по правой части и начальным данным, а также сходится к точному решению с первым порядком. Конечно, если не известно точное решение, а как правило это справедливо для нелинейных уравнений, то анализ конечно-разностных схем усложняется. Однако всегда можно построить схему более высокого порядка точности, например, используя метод двойного счета или Ричардсона [11].

Литература

1. Тарасов В.Е. Модели теоретической физики с интегро-дифференцированием дробного порядка. М.–Ижевск: Ижевский институт компьютерных исследований, 2011. 567 c.
2. Вольтерра В. Теория функционалов, интегральных и интегро-дифференциальных уравнений. М.: Наука, 1982. 304 с.
3. Учайкин В.В. Метод дробных производных. Ульяновск: Артишок, 2008. 510 с.
4. Самко С.Г., Килбас А.А., Марычев О.И. Интегралы и производные дробного порядка и некоторые их приложения. Минск: Наука и техника, 1987. 688 с.
5. Нахушев А.М. Дробное исчисление и его приложения. М.: Физматлит, 2003. 272 с
6. Паровик Р.И. Математическое моделирование эредитарного осциллятора // Компьютерные исследования и моделирование. 2015. Т. 7., №5. С. 1001-1021.
7. Паровик Р.И. Конечно-разностные схемы для фрактального осциллятора с переменными дробными порядками // Вестник КРАУНЦ. Физико-математические науки. 2015. 2(11). С. 88-95. DOI: 10.18454/2079-6641-2015-11-2-88-95.
8. Паровик Р.И. О численном решении уравнения фрактального осциллятора с производной дробного переменного порядка от времени // Вестник КРАУНЦ. Физико-математические науки. 2014. 1(8). С. 60-65. DOI: 10.18454/2079-6641-2014-8-1-60-65.
9. Самарский А.А. Теория разностных схем. М.: Наука, 1977. 656 с.
10. Паровик Р.И. Математическое моделирование линейных эредитарных осцилляторов. Петропавловск-Камчатский: КамГУ им. Витуса Беринга, 2015. 178 с.
11. Петров И.Б., Лобанов А.И. Лекции по вычислительной математике. М.: БИНОМ, 2006. 523 с.

References

1. Tarasov V.E. Modeli teoreticheskoj fiziki s integro-differencirovaniem drobnogo porjadka. M.–Izhevsk: Izhevskij institut komp'juternyh issledovanij, 2011. 567 c.
2. Vol'terra V. Teorija funkcionalov, integral'nyh i integro-differencial'nyh uravnenij. M.: Nauka, 1982. 304 s.
3. Uchajkin V.V. Metod drobnyh proizvodnyh. Ul'janovsk: Artishok, 2008. 510 s.
4. Samko S.G., Kilbas A.A., Marychev O.I. Integraly i proizvodnye drobnogo porjadka i nekotorye ih prilozhenija. Minsk: Nauka i tehnika, 1987. 688 s.
5. Nahushev A.M. Drobnoe ischislenie i ego prilozhenija. M.: Fizmatlit, 2003. 272 s
6. Parovik R.I. Matematicheskoe modelirovanie jereditarnogo oscilljatora // Komp'juternye issledovanija i modelirovanie. 2015. T. 7., №5. S. 1001-1021.
7. Parovik R.I. Konechno-raznostnye shemy dlja fraktal'nogo oscilljatora s peremennymi drobnymi porjadkami // Vestnik KRAUNC. Fiziko-matematicheskie nauki. 2015. 2(11). S. 88-95. DOI: 10.18454/2079-6641-2015-11-2-88-95.
8. Parovik R.I. O chislennom reshenii uravnenija fraktal'nogo oscilljatora s proizvodnoj drobnogo peremennogo porjadka ot vremeni // Vestnik KRAUNC. Fiziko-matematicheskie nauki. 2014. 1(8). S. 60-65. DOI: 10.18454/2079-6641-2014-8-1-60-65.
9. Samarskij A.A. Teorija raznostnyh shem. M.: Nauka, 1977. 656 s.
10. Parovik R.I. Matematicheskoe modelirovanie linejnyh jereditarnyh oscilljatorov. Petropavlovsk-Kamchatskij: KamGU im. Vitusa Beringa, 2015. 178 s.
11. Petrov I.B., Lobanov A.I. Lekcii po vychislitel'noj matematike. M.: BINOM, 2006. 523 s.