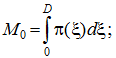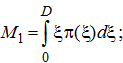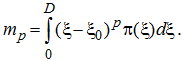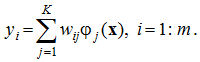NEURAL NETWORK SCHEME FOR AERIAL TARGET RECOGNITION BY RADAR RANGE PROFILES

Фам Фыонг Кыонг

Стажер, Московский технологический университет (МИРЭА)

НЕЙРОСЕТЕВАЯ СХЕМА РАСПОЗНАВАНИЯ ВОЗДУШНЫХ ЦЕЛЕЙ ПО РАДИОЛОКАЦИОННЫМ ДАЛЬНОСТНЫМ ПОРТРЕТАМ

Аннотация

Обсуждается проблема автоматического распознавания воздушных целей на основе анализа их радиолокационных дальностных портретов. Процедура радиолокационного распознавания включает последовательное решение двух задач. Первая задача состоит в формировании классификационных признаков воздушных целей по дальностным портретам, позволяющих отличать друг от друга. Вторая задача – нейросетевая идентификация дальностных портретов  по совокупности полученных признаков. Рассматривается метод классификации на основе радиальных базисных сетей.

Ключевые слова: радиолокация, распознавание воздушных целей, радиолокационные дальностные портреты, морфологические и геометрические информативные признаки, нейросетевые алгоритмы идентификации, радиальая базисная сеть.

Pham Phuong Cuong

Apprentice, Moscow Technological University

NEURAL NETWORK SCHEME FOR AERIAL TARGET RECOGNITION BY RADAR RANGE PROFILES

Abstract

This article discusses the problem of automatic aerial target recognition based on analysis of radar range profiles and questions of informative signature formation. The procedure of radar recognition includes sequential two tasks. The first task is to build classification signatures of aerial targets using range profiles, which allow to distinguish targets from each other. The second task – neural network identification of range profiles by gather of obtained signatures. Classification method based on radial basis neural networks are examined.

Keywords: radar, aerial taget recognition, radar range profiles, morphological, geometric informative signatures, neural network algorithm for indentify, radial basis neural network.

Радиолокация - это область радиоэлектроники, занимающаяся обнаружением объектов (целей), определением их пространственных координат, параметров движения и физических характеристик с помощью радиотехнических средств и методов [1]. Перечисленные задачи решаются в процессе радиолокационного наблюдения, а устройства, предназначенные для этого, называются радиолокационными станциями (РЛС).

Необходимую для распознавания протяженных воздушных целей (ВЦ) информацию могут давать радиолокационные дальностные портреты (ДП), называемых в англоязычной литературе «range profile» [2–4]. В настоящей статье исследуются вопросы построения систем автоматического распознавания ВЦ на основе анализа их ДП.

В выполненных исследованиях использовалась программа моделирования ДП воздушных целей «Radar Target Back Scattering Simulation» (BSS), разработанная Я.Д.Ширманом и его коллегами [5].

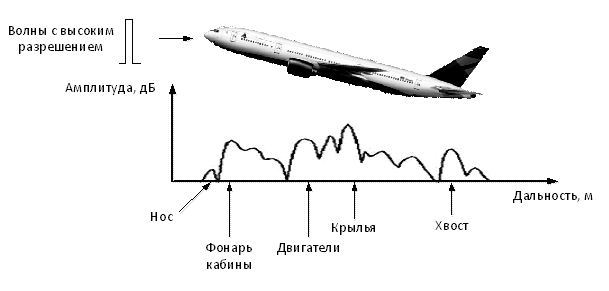
Рис.1 -  Дальностный портрет ЛА

Радиолокационные дальностные портреты

Дальностный портрет (дальностный профиль) является одномерной характеристикой радиолокационных целей. Это отклик объекта наблюдения при облучении широкополосным импульсом во временной области. Рис. 1 иллюстрирует принцип формирования радиолокационного дальностного портрета летательных аппаратов (ЛА) [2].

На каждом дальностном отсчете амплитуда полученного сигнала дает силу отраженного сигнала. На рис. 1 показаны основные части самолета, которые создают ДП.

Отметим, что видимая длина объектов на ДП может отличаться от его физической длины из-за двух эффектов. Сигнал, отражающийся в строну РЛС, может далее подвергаться отражению от других рассеивателей цели, вследствие чего повышается временная задержка, которая и появляется в структуре ДП. Второй эффект обусловлен сокрытием одних частей самолета другими: некоторая часть самолета может быть скрыта его большой частью, которая находится между первой и РЛС. В итоге уменьшается энергия радиоволн, которые дойдут до цели и будут отражены обратно к РЛС. Например, фюзеляж или крылья самолета могут скрывать его хвост.

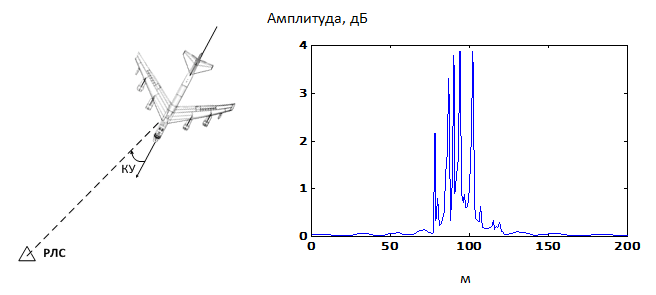
На рис. 2 в качестве примера приведен ДП бомбардировщика B-52.

Рис. 2 - Дальностный портрет бомбардировщика B-52

Эффект отражения радиоволн от ВЦ в сторону РЛС зависит от курсового угла (КУ) - угла между продольной осью ЛА и направлением на наблюдателя в плоскости истинного горизонта последнего, отсчитываемый по ходу часовой стрелки. Отметим, что ДП на рис. 2 отвечает КУ=20°.

Далее дальностные портреты рассматриваются как одномерные функции:

A=π(ξ).

где ξ  - дальность отсчета (м), A - амплитуда отклика (дБ).

Процедура распознавания ВЦ на основе анализа их дальностных портретов предполагает решение двух подзадач:

• формирование комплекса информативных признаков ВЦ по ее ДП;
• классификацию ВЦ на основе полученных информативных признаков.

Схема распознавания воздушных целей

Введем обозначения:

• Ω - множество наблюдаемых ВЦ;
• ω∈Ω - объекты наблюдения;
• AC - алфавит классов ВЦ:

;

•  - классы;
• Θ - алфавит меток (имен) классов ВЦ:

;

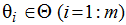• - метки классов;
• П - множество дальностных портретов ВЦ;
• π∈П - дальностные портреты.
• X - признаковое пространство ВЦ.

Пространство  определяется выбором информативных признаков . При этом объекты наблюдения представляются кортежем

.                                                  (1)

Каждая ВЦ относится к некоторому классу и, следовательно, ей априори соответствует определенная метка класса:

ω → θ.

Алгоритм классификации осуществляет функциональное преобразование

x → y,

т.е. для каждого входного образа x∈X вычисляет соответствующую метку класса y∈Θ, которая и присваивается наблюдаемой ВЦ.

В случае правильной классификации

y=θ.

Надежность процедуры распознавания в значительной мере зависит от выбора системы информативных признаков. В настоящей работе для идентификации ДП ВЦ предлагается применять следующие группы признаков:

• морфологические;
• геометрические.

Морфологические информативные признаки

Самым простым морфологическим признаком ДП является число пиков  в его структуре. Следует учитывать лишь доминирующие пики, которые значительно превышают по амплитуде шумы и помехи.

Другая характеристика ДП основана на ранжировании составляющих его пиков по амплитуде. Набор применяемых информативных признаков должен быть инвариантным по отношению к действию данных факторов. Поэтому для анализа ДП неприемлемо прямое применение амплитудных значений пиков в силу их зависимости от ряда не учитываемых возмущающих и искажающих факторов в принимаемом эхо-сигнале. Предлагается вместо амплитудных значений пиков применять их ранги. Таким образом, речь идет о структурной идентификации ДП посредством использования ранговых шкал.

Ранги пиков определяются следующим образом. Положим, в ДП выделены m пиков с амплитудами . Из этих величин составляется вариационный ряд в порядке убывания. Далее элементы ряда нумеруются от 1 до m. Наконец, порядковый номер каждого элемента в вариационном ряду определяет его ранг:

.

В итоге получаем наборы рангов пиков

.

Так для ДП, представленного на рис. 4, 

Геометрические информативные признаки

Геометрические признаки представляют глубину D и моментные характеристики ДП.

Определим глубину ДП D как расстояние между крайними отчетами в отраженном радиосигнале. Данные отсчеты необходимо выделять на фоне помех.

Другие геометрические характеристики ДП:

а) начальный момент нулевого порядка:

б) начальный момент первого порядка:

в) положение центра тяжести ДП:

г) центральный момент p-го порядка :

Определенные выгоды при анализе ДП могут давать безразмерные величины, построенные по данным показателям. В частности, сюда относятся

д) относительное положение центра тяжести ДП:

е) центральные нормированные моменты:

Данные показатели инвариантны к мощности принимаемого сигнала.

К примеру, для ДП самолета В-52, представленного на рис. 2, , .

Исследования показывают, что морфологических и геометрических характеристик ДП достаточно для эффективного распознавания ВЦ.

Динамический аспект радиолокационного наблюдения

Форма и метрические характеристики ДП зависят от курсового угла движения ВЦ. В связи с этим далее будем его рассматривать как двумерную функцию:

где γ - курсовой угол (°), ξ - дальность отсчета, A - амплитуда отклика.

Совокупность всех информативных признаков ВЦ представим кортежем:

                                                      (2)

где  - соответственно кортежи морфологических и геометрических признаков:

                            (3)

Надежность и качество распознавания в значительной мере зависят от выбора системы информативных признаков для рассматриваемых классов объектов наблюдения. Поскольку необходимая для обработки радиолокационная информация получается в процессе радиолокационного слежения за движущейся ВЦ, то последняя порождает динамический образ в рассматриваемом классе задач распознавания. С учетом этого для решения задачи динамического распознавания ВЦ предлагается применять механизм агрегирования радиолокационной информации, полученной в различные последовательные моменты времени наблюдения.

Пусть в процессе радиолокационного наблюдения фиксируется состояние ВЦ в моменты времени

причем им отвечают курсовые углы

Тогда на выходе приемника РЛС мы получаем семейство ДП:

                                             (4)

Далее T  - множество моментов времени съема радиолокационной информации:

Блок-схема системы динамического распознавания ВЦ

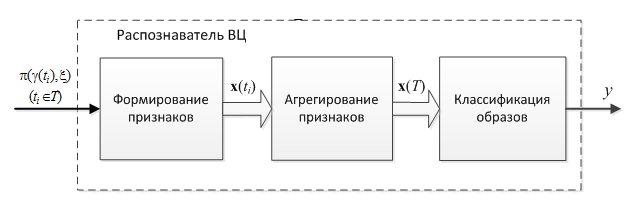
Предлагаемую концепцию динамического распознавания ВЦ представляет блок-схема на рис. 3.

Рис. 3 - Схема распознавания ВЦ

Здесь для каждого ДП в (4) в соответствии с (1)–(3) формируется вектор признаков  которые далее объединяются в один супервектор (посредством конкатенации векторов):

                                      (5)

Теперь мы имеем дело с расширенным пространством признаков  - декартовой степенью исходного пространства признаков:

где

Именно вектор (5) и является динамическим образом ВЦ.

Классификация ВЦ на основе радиальных базисных сетей

Решения задачи классификации динамических образов можно основывать на технологиях искусственных нейронных сетей (НС). В работе исследовались функциональные возможности радиально-базисных (RBF - Radial Basis Functions) НС.

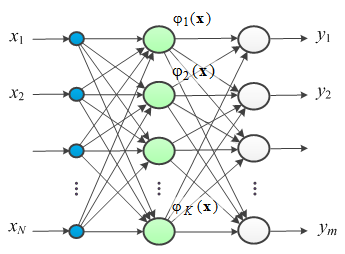
RBF-сети относится к классу сетей прямого распространения. Архитектура сети представляется двумя слоями нейронов (рис. 4), без учёта входного слоя, выполняющего роль распределителя входных сигналов. Скрытые нейроны реализуют радиальные базисные функции активации.

Рис. 4 - Архитектура сети RBF

Радиально-базисные функции имеют вид

где c - центр функции, причем двойные прямые скобки  обозначают норму вектора. Предполагается, что функция монотонно убывает с удалением от центра c. Ее можно интерпретировать как потенциал.

Наиболее распространённым видом радиальных функций активации является функция Гаусса [6]:

где σ - параметр, определяющий размер активной области функции.

В сети функция активации j-го нейрона  определяется его центром . Выход сети формируется выходным слоем линейных нейронов:

Таким образом, он определяется матрицей весовых коэффициентов .

Роль скрытых нейронов заключается в группировке входных векторов на K классов, причем каждый класс отграничен в пространстве входных векторов некоторой изопотенциальной поверхностью

охватывающей центр класса .

В процессе обучения происходит кластеризация обучающей выборки (ОВ) с выделением K классов, область локализации которых определяется соответствующей радиальной функцией . Процесс кластеризации на каждой итерации предполагает выделение радиального нейрона, вектор весов которого в наименьшей степени отличается от входного вектора x, и смещение вектора весов данного нейрона в сторону этого вектора. При этом применяются различные меры близости векторов, из которых наиболее часто встречается эвклидова.

По завершению разделения входного пространства происходит настройка весовой матрицы W выходного слоя. Задача его обучения сводится к минимизации расхождения фактической реакции сети и желаемой.

Раздельное обучение предполагает вначале разделение входного пространства на кластеры в радиальном слое, а затем обучение с учителем выходного линейного слоя.

Процесс обучения сети RBF сводится:

• к подбору центров  и параметров σ_j  формы базисных функций;
• к подбору весов нейронов выходного слоя.

Частным случаем RBF-сетей являются вероятностные нейронные сети (PNN - Probabilistic Neuron Networks) [7]. В структуре сетей PNN второй слой в отличие от сетей RBF представлен нейронами конкурирующего типа, которые подсчитывают условную вероятность принадлежности входного вектора к одному из выходных классов. При этом активируется только нейрон, суммарное значение входных сигналов которого наибольшее. Поэтому в качестве функции активации выходных нейронов применяется пороговая.

Характерной чертой PNN является то, что количество нейронов скрытого слоя берётся равным числу элементов обучающей выборки. Таким образом, учитывается влияние каждого примера из ОВ, а роль второго слоя сводится к объединению в заданные классы групп входных векторов из ОВ.

Результаты вычислительных экспериментов

В вычислительных экспериментах использовалась программа BSS, позволяющая генерировать эталонные ДП воздушных целей 10-и типов.

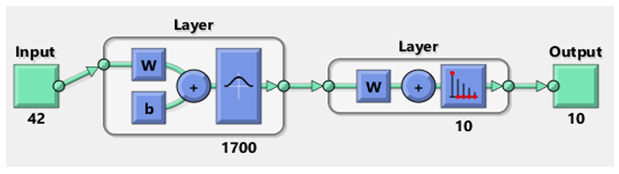
В принятой схеме распознавания (рис. 3) осуществлялось агрегирование входных данных для трех последовательных моментов времени, т.е. d=3. Поскольку размерность вектора признаков равна n=14, то используемая в классификаторе сеть PNN имеют N=42 входа. Число выходов равно m=10.

Обучающая выборка состояла из 2000 примеров, причем для каждого из 10 типов ВЦ использовалось 200 образцов ДП. Выборка была поделена на две части: большая часть (1700 примеров) предназначалась для настройки НС, а меньшая часть (300 примеров) - для тестирования НС. Вследствие этого в радиальный базисный слой сети включал K=1700 нейронов.

Моделирование НС осуществлялось в среде системы MATLAB - использовался пакет Neural Network Toolbox [8]. Архитектуру моделируемой НС демонстрирует рис. 5.

Рис. 5 - Архитектура сети PNN

Отметим, что, несмотря на большое количество нейронов, сеть PNN очень быстро обучается. Результаты тестирования НС подтверждают ее безошибочную работу.

Литература

1. Бакулев П.А. Радиолокационные системы. – М. : Радиотехника, 2007. - 376 с.
2. Tait P. Introduction to radar target recognition. – London: Institution of Electrical Engineers, 2005. IET radar series no. 18. - 396 p.
3. Лещенко С.П. Развитие теории и техники радиолокационного распознавания воздушных целей // Прикладная радиоэлектроника. 2009. Т. 8, № 4. - C. 490-496.
4. Тоцкий А.В., Молчанов П.А., Поспелов Б.Б. Распознавание летательных аппаратов по радиолокационным дальностным профилям // Авиационно-космическая техника и технология. 2010. № 5 (72). – С. 77–82.
5. Ширман Я.Д., Горшков С.А., Лещенко С.П., Братченко Г.Д., Орленко В.М. Методы радиолокационного распознавания и их моделирование // Зарубежная радиоэлектроника. 1996. № 11. – C. 3–63.
6. Хайкин С. Нейронные сети: полный курс. – М.: Изд. дом «Вильямс». 2006. – 1104 c.
7. Wasserman P.D. Advanced methods in neural computing. – New York: Van Nostrand Reinhold, 1993. – P. 35–55.
8. Медведев B.C., Потемкин В.Г. Нейронные сети. MATLAB 6. – М.: ДИАЛОГ-МИФИ. 2010. – 496 с.

References

1. Bakulev P.A. Radiolokacionnye sistemy (Radar systems). M. : Radiotekhnika, 2007. - 376 s.
2. Tait P. Introduction to radar target recognition. London: Institution of Electrical Engineers, 2005. IET radar series no. 18. - 396 p.
3. Leshchenko S.P. Razvitie teorii i tekhniki radiolokacionnogo raspoznavaniya vozdushnyh celej (Development of the theory and technology of aerial taget radar recognition) // Prikladnaya radioehlektronika. 2009. T. 8, № 4. - C. 490-496.
4. Tockij A.V., Molchanov P.A., Pospelov B.B. Raspoznavanie letatel'nyh apparatov po radiolokacionnym dal'nostnym profilyam (Aircraft recognition using radar range profiles) // Aviacionno-kosmicheskaya tekhnika i tekhnologiya. 2010. № 5 (72). - S. 77-82.
5. D. Shirman, S.A. Gorshkov, S.P. Leshchenko, G.D. Bratchenko, V.M. Orlenko Metody radiolokacionnogo raspoznavaniya i ih modelirovanie (Methods of radar recognition and simulation) // Zarubezhnaya radioehlektronika. 1996. № 11. - C. 3-63.
6. Hajkin S. Nejronnye seti: polnyj kurs (Neural networks: complete course) – M.: Izd. dom «Vil'jams». – 1104 c.
7. Wasserman P.D. Advanced methods in neural computing. – New York: Van Nostrand Reinhold, 1993. – P. 35–55.
8. Medvedev B.C., Potemkin V.G. Nejronnye seti. MATLAB 6 (Neural networks. MATLAB 6) – M.: DIALOG-MIFI. 2010. – 496 s.