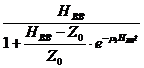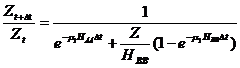MODELLING OF CHANGE OF LEVEL OF GROUND WATERS AT CONTINUOUS WATER RETURN
Василенков В.Ф.1, Дёмина О.Н.2, Аксёнов Я.А.3
1 доктор технических наук, 2 кандидат технических наук, 3 аспирант, ФГБОУ ВО Брянский государственный аграрный университет
МОДЕЛИРОВАНИЕ ИЗМЕНЕНИЯ УРОВНЯ ГРУНТОВЫХ ВОД ПРИ ПОСТОЯННОЙ ВОДООТДАЧЕ
Аннотация
В статье предложена модель, которая позволяет получить достоверную информацию об изменения уровня грунтовых вод и предложить обоснование интенсивности водных мелиораций агроландшафтов, оптимизации расчётов сельскохозяйственного дренажа и корректировки управления водным режимом сельскохозяйственных угодий. Схематично представлены изменения в системе грунтовые воды - внешняя среда за счет взаимодействия двух обобщенных кинетических единиц - грунтового потока и осушенной зоны. Схематизация отекания грунтовых вод с водосбора позволяет наглядно прийти к уравнению баланса. Дана методика и пример определения параметров модели изменения уровня грунтовых вод. Согласие результатов расчёта и эксперимента даёт все основы для практического использования модели.
Ключевые слова: уровень грунтовых вод, коэффициент водоотдачи, осушенная зона.
Vasilenkov V.F.1, Demina O.N.2, Aksyonov Y.A.3
1 PhD in Engineering, 2 PhD in Engineering, 3 Postgraduate student, FSBEI HE Bryansk State Agrarian University
MODELLING OF CHANGE OF LEVEL OF GROUND WATERS AT CONTINUOUS WATER RETURN
Abstract
There is proposed a model that allows you to obtain reliable information on the changes in the groundwater level and offer justification for the intensification of water reclamation of agricultural landscapes, optimizing agricultural drainage calculations and adjustments manage of the water regime of agricultural land. It is schematically shown the changes in the system of groundwater - the external environment due to the interaction of two generalized kinetic units - ground flow and drainage area. Schematization of the swelling groundwater from catchment allows visually to come to the equation of balance. There is given the technique and an example of determining of the parameters of the model of groundwater level changes. The agreement of results of calculation and experiment gives all the basics for the practical use of the model.
Keywords: groundwater level, water loss rate, drained area.
Основной задачей в вопросах устойчивого развития агропромышленного комплекса является достижение нормативной урожайности и высокого качества продукции, значительной экономии трудовых, энергетических ресурсов и охрана окружающей среды в Брянской области [1-3], в том числе и за счёт решения проблем обоснования необходимости и интенсивности водных мелиораций агроландшафтов, оптимизации расчётов сельскохозяйственного дренажа и управления водным режимом сельскохозяйственных угодий. Вышеуказанные проблемы возможно проработать, осуществив моделирование изменения уровня грунтовых вод: сложных взаимоотношений водного тела, системы водосбора и окружающей среды [4].
Предположим, что все изменения в системе грунтовые воды - внешняя среда происходят в результате взаимодействия только двух обобщенных кинетических единиц - грунтового потока и осушенной зоны [5]:
Z + Н → Z + Z ( 1.1)
где Z, Н - толщина осушенной зоны и грунтового потока в створе наблюдательной скважины в см.
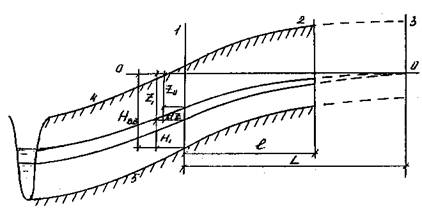
Кривые уровней вдоль плановой линии тока на водосборе в разные моменты времени гипотетически продолжаются до точки пересечения (точка "О"), через которую проводится горизонтальная линия 0-0 - ось отсчета мощности осушенной зоны "Z" (см. рисунок 1). Положительное направление вертикальной оси OZ принято вниз. Используя уравнение баланса и закон Дарси, принимая поверхность грунтовых вод плоской, скорость изменения уровней по схеме (рис. 1) можно описать уравнением:
Рис. 1. Схематизация отекания грунтовых вод с водосбора
1 - створ наблюдательной скважины; 2- створ границы водосбора (водораздел).
где φ - характеризует форму кривой депрессии, находится из пропорции; δ - коэффициент водоотдачи; ![]() - расстояние по линии тока от створа наблюдательной скважины до водораздела (см. рис. 1);
- расстояние по линии тока от створа наблюдательной скважины до водораздела (см. рис. 1);
L - расстояние от створа наблюдательной скважины до гипотетической точки пересечения депрессионных кривых (см. рис. 1);
Z/L- изменяющийся во времени уклон поверхности грунтового потока;
k - коэффициент фильтрации грунта; в - ширина потока;
Интегрируя уравнение (1.3) при начальных значениях t=0, Z=Zо получаем:
Полученное выражение (1.4), описывающее закон снижения уровня грунтовых вод во времени, дает кинетические кривые близкие по форме S – образным кривым. Для экспериментальной проверки математической модели использованы измерений, проведенных в наблюдательных скважинах метеостанций Сухиничи Калужской области, Чернь и Узловая Тульской области, Ряжск Рязанской области и др. С точки зрения кинетики изменения уровней экспериментальных данных, полученных разными метеостанциями, практически не отличаются.
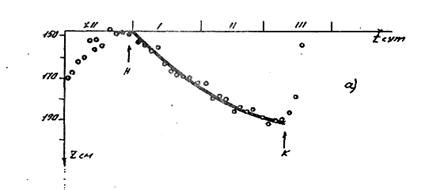
Рисунок 1. Депрессионная кривая, МС Ряжск, скв. 142, 1990 г.
На S – образных кинетических кривых можно выделить четыре периода: начальный и период инерции, период регулярного снижения уровней, равновесие или стационарная фаза и период подъема уровней. Деление кинетической кривой не означает, что предполагаются какие-то особые законы движения воды в каждый период. В начальном периоде происходит перестройка в системе, вызванная сменой направления движения воды от подъема к спаду. Период регулярного снижения уровней можно охарактеризовать как протекание последовательных переходов грунтовых вод в капиллярную кайму и от капиллярной каймы к осушенному грунту с влажностью, близкой к ППВ, причем в установившемся режиме. Прогрессивно возрастающее замедление снижения уровня приводит к стабилизации уровня на определенной отметке. Однако, при анализе экспериментальных данных выявлен факт установления фазы стационарного состояния на разных по годам отметках, который не объясняется наличием водообмена между водоносными пластами. По-видимому, существуют другие причины, лимитирующие снижение уровня, в зависимости от меняющихся ежегодно условий.
Для определения параметров модели на основании полученных в эксперименте данных целесообразно уравнение (1.4) преобразовать, приведя к удобному для анализа линейному виду. Разделим левую и правую части уравнения (1.3) на Z получаем:
Из уравнения (1.5) следует, что относительная (логарифмическая) скорость снижения уровня
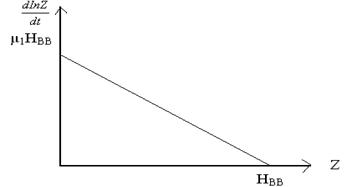
в отличие от абсолютной dZ/dt является линейной убывающей функцией все увеличивающейся в процессе стекания грунтового потока мощности осушенной зоны. Это значит, что S - образные кривые описываемые уравнением (1.4) могут быть преобразованы в прямую линию при представлении результатов в координатах ![]() . При экстраполяции такой прямой до пересечения ее с осью ординат, где Z=0 отсекается отрезок численно равный μ1 НВВ; при экстраполяции прямой до пересечения с осью абсцисс, где
. При экстраполяции такой прямой до пересечения ее с осью ординат, где Z=0 отсекается отрезок численно равный μ1 НВВ; при экстраполяции прямой до пересечения с осью абсцисс, где ![]() , отсекается отрезок равный Нвв (рис. 2).
, отсекается отрезок равный Нвв (рис. 2).
Рис.2. Изменение логарифмической скорости снижения уровней.
Если полученная на основании данных эксперимента зависимость
линейна, то это значит, что процесс снижения уровней от начала до конца действительно зависит только от тех свойств, которые при построении модели рассматривались как существенные и характеризуется константами μ1; Нвв. Это свидетельствует также о том, что условия стекания влияющие на величину параметров кинетики, за весь период стекания существенно не менялись.
Необходимую для определения параметров μ1Нвв и Нвв зависимость ![]() можно получить графически, продифференцировав депрессионную кривую, отражающую изменение уровней во времени.
можно получить графически, продифференцировав депрессионную кривую, отражающую изменение уровней во времени.
Необходимую для определения параметров μ1Нвв и Нвв зависимость ![]() можно получить графически продифференцировав депрессионную кривую, отражающую изменение уровней во времени. Для этого вместо значений мгновенной скорости
можно получить графически продифференцировав депрессионную кривую, отражающую изменение уровней во времени. Для этого вместо значений мгновенной скорости ![]() или
или ![]() приходится рассчитывать величину средней (для какого-то конечного промежутка времени) скорости
приходится рассчитывать величину средней (для какого-то конечного промежутка времени) скорости ![]() или
или ![]() .
.
Переход от бесконечно малых к конечным величинам в ряде случаев сопровождается значительным искажениям реально существующей зависимости. Искажение исследуемой зависимости бывает тем сильнее, чем больше интервал времени между определениями положения уровня.
Преобразовав выражение (1.4.) подстановкой Ztи Zt+∆t, получим:
Отсюда, зная величину ∆t, можно найти значения параметров μ1Нвв и НВВ. Определение параметров μ1Нвв и НВВ таким способом не накладывает никаких ограничений на величину интервала времени между измерениями уровня, требуется лишь, чтобы он был одинаковым на протяжении всего периода измерений. Если ∆t будет постоянно, то уравнение является линейным. Следовательно, при представлении экспериментальных данных в виде зависимости величины φ от Z прямая на оси абсцисс будет отсекать отрезок, численно равный Нвв, а на оси ординат – отрезок ![]() (см. рис.3).
(см. рис.3).
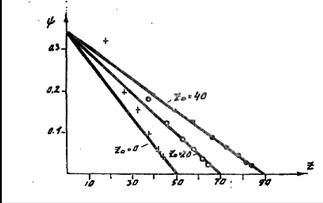
Примеры определения параметров μ1Нвв; НВВ; Zо по экспериментальным данным приведены на рис. 3. Чтобы исключить влияние испарения и инфильтрационного питания, для расчета взяты зимние безоттепельные периоды.
Рис. 3. Зависимость φ= ![]() от Z . Линеаризация, депрессионной кривой при ∆t = 10 сут, Zо = 40 см, φ= 0.34.
от Z . Линеаризация, депрессионной кривой при ∆t = 10 сут, Zо = 40 см, φ= 0.34.
Достигнуть большей мощности осушенного слоя Нвв при одном и том же Нвв можно оптимизацией тех условий стекания, от которых зависит величина коэффициента полноты осушения. Величина коэффициента полноты осушения является наиболее адекватным критерием степени удаленности условий стекания грунтовых вод от оптимума.
Согласие результатов расчёта и эксперимента даёт все основы для практического использования модели. Предложенная модель позволяет получить достоверную информацию об изменения уровня грунтовых вод и предлагать интенсивность водных мелиораций агроландшафтов, оптимизировать расчёты сельскохозяйственного дренажа и управлять водным режимом сельскохозяйственных угодий.
Литература
- Бельченко С.А.Развитие АПК Брянской области/ Бельченко С.А., Белоус И.Н., Наумова М.П. Вестник Брянской государственной сельскохозяйственной академии. 2015. № 2-1 (2015). С. 32-36.
- Концепция «Обеспечение устойчивого развития агропромышленного производства в условиях техногенеза»/ Романенко Г.А., Фисинин В.И., Иванов А.Л., Жученко А.А., Кормановский Л.П., Сизенко Е.И., Ушачев И.Г. и др.- РАСХН.– М., 2003. – 66 c.
- Белоус, Н. М. Озимые зерновые культуры: биология и технологии возделывания: монография / Н. М. Белоус, В. Е. Ториков, Н. С. Шпилёв, О. В. Мельникова, Г. П. Малявко, М. П. Наумова, О. М. Нестеренко, О. М. Михайлов. – Брянск, 2010. – 138 с.
- Харкевич Л.П. Воздействие агротехнических и агрохимических мероприятий на урожайность многолетних трав и плодородие почвы/ Харкевич Л.П., Белоус Н.М., Смольский Е.В., Чесалин С.Ф. Плодородие. 2013. № 4 (73). С. 25-27.
- Роде А.А. Основы учения о почвенной влаге. Гидрометеоиздат, 1965.
References
- Belchenko S.A.Razvity agrarian and industrial complexes of Bryansk area / Belchenko C. And., Belous I.N., Naumova M.P. Bulletin of Bryansk state agricultural academy. 2015. No. 2-1 (2015). P. 32-36.
- Concept "Providing a sustainable development of agro-industrial production in the conditions of a tekhnogenez" / Romanenko G. A., Fisinin V. I., Ivanov A.L., Zhuchenko A.A., Kormanovsky L.P., Sizenko E.I., Ushachev I.G., etc. Moscow, 2003.-66 pages.
- Belous, N. M. Winter grain crops: biology and technologies of cultivation: monograph / N. M. Belous, V. E. Torikov, N. S. Shpilyov, O. V. Melnikova, G. P. Malyavko, M. P. Naumova, O. M. Nesterenko, O. M. Mikhaylov. – Bryansk, 2010. – 138 pages.
- Harkevich L.P. Impact of agrotechnical and agrochemical actions on productivity of long-term herbs and fertility Soil / Harkevich L.P., Belous N. M., Smolsky E.V., Chesalin S.F. Fertility. 2013. No. 4 (73). Page 25-27.
- Sort A.A. Doctrine bases about soil moisture. Gidrometeoizdat, 1965.