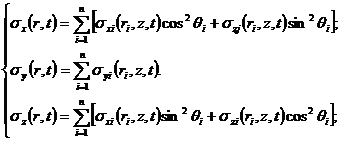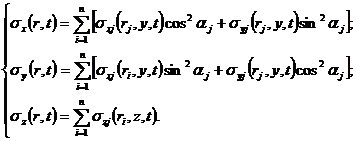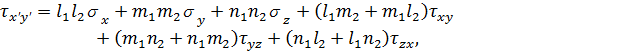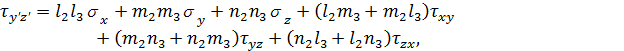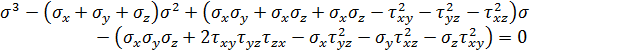CALCULATION OF WAVE FIELD STRENGTHIN THE EXPLOSION OF BLASTHOLE CHARGES GIVEN THE DIRECTION OF EXPLISIVE ACTION

Парамонов Г.П.¹, Должиков В.В.²

¹ Доктор технических наук, профессор, Национальный минерально-сырьевой университет «Горный», ² Аспирант, Национальный минерально-сырьевой университет «Горный»

МЕТОДИКА РАСЧЕТА ВОЛНОВОГО ПОЛЯ НАПРЯЖЕНИЯ ПРИ ВЗРЫВЕ СКВАЖИННЫХ ЗАРЯДОВ С УЧЕТОМ НАПРАВЛЕННОСТИ ДЕЙСТВИЯ ВЗРЫВА

Аннотация

В работе приводятся результаты теоретического исследования формирования волнового поля напряжения при взрыве системы скважинных зарядов. Предложена методика расчета волнового поля напряжений. Установлено влияние интервала замедления между рядами скважин и направлением инициирования на параметры волн напряжений.

Ключевые слова: дробление, волновой фактор взрыва, схема инициирования, поле напряжений, направление действия взрыва, интервал замедления.

Paramonov G.P.¹, Dolzhikov V.V.²

¹ PhD in Engineering, professor, National Mineral Resources University (Mining University), ² Postgraduate student, National Mineral Resources University (Mining University)

CALCULATION OF WAVE FIELD STRENGTHIN THE EXPLOSION OF BLASTHOLE CHARGES GIVEN THE DIRECTION OF EXPLISIVE ACTION

Abstract

The paper presents the results of theoretical studies of formation of the wave field system voltage in the explosion of blasthole charges. The method of calculation of wave stress field.The effect of slowing down the interval between the rows of holes and direction of the initiation of the parameters of stress waves.

Keywords: crushing, the wave of the explosion factor, initiating the scheme, the stress field, the direction of action of the explosion, the deceleration interval.

Одна из основных задач при производстве взрывных работ – получить горную массу определенного гранулометрического состава. Решение этой задачи возможно на основе полного изучения механизма разрушения среды при приложении импульсивных нагрузок, который позволяет определить оптимальные параметры импульса в конкретных горнотехнических условиях. Важную роль в механизме разрушения горных пород взрывом играют волны напряжения.

Методика расчета параметров волн напряжения была разработана авторами работ [1,2]. Данная методика cсовершенствовалась в работах [3,4,5].

Рассмотренные алгоритмы и программы были сильно ориентированы на типы вычислительной техники и были не очень приспособлены к проведению большого объема расчётов.

Автор работы [3] попытался учесть скорость детонации и реальную длину заряда. Он рассчитал геометрические параметры волнового фронта, возникающего вокруг заряда цилиндрической симметрии, ввёл и экспериментально определил скорость уменьшения конического участка волнового фронта. Однако, на этапе определения влияния конструктивных параметров заряда цилиндрической симметрии на формирование поля напряжений в безграничной среде, он не учёл такой важный параметр как диаметр заряда. В результате, предложенный им расчёт даёт возможность лишь качественно оценить форму волнового фронта, в зависимости от длины заряда и скорости детонации.

Автором работы [4] были устранены эти недостатки, но рассматривала процесс формирования поля напряжений от 1 удлинённого заряда, что недостаточно полно описывает реальную картину влияния напряжений на разрушение горного массива, т.к. в практике используется групповое взрывание скважинных зарядов.

В работе [5] предложена методика численного расчета параметров волнового поля напряжений от четырех скважинных зарядов. Однако, это методика не учитывала такие важные параметры БВР, как направление инициирования, количество точек инициирования. Кроме того, рассчитывались только радиальные напряжения или составляющие волны напряжений по координатным осям, что затрудняло анализ по всему расчётному полю.

В связи с изложенным, нами предлагается методика, позволяющая не только считать напряженное состояние среды от взрыва скважинного заряда или простейших систем скважинных зарядов, но и численно считать главные напряжения с учетом расположения точек инициирования, последовательности инициирования, интервала замедления между зарядами, неограниченного числа скважин, различных ВВ, конструкций, в разных точках плоскости.

Алгоритм расчёта полей напряжения достаточно прост и состоит из следующих шагов.

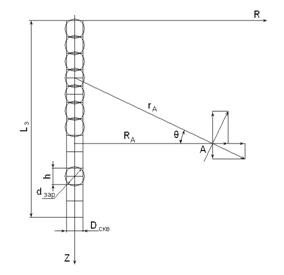
Шаг 1. Для некоторой интересующей нас точки наблюдения рассчитываем зависимости напряжения от времени для единичного скважинного заряда k₁ в координатах (R_k1,φ) (рис.1). Напряжения от каждого элементарного заряда рассчитываютсяпо методике, представленной в работе [1] и далее они пересчитываются в системе координат (R_k1,N,Z) по формулам:

  

Рис. 1. - Схема расчета поля напряжений, взрывом скважинного заряда

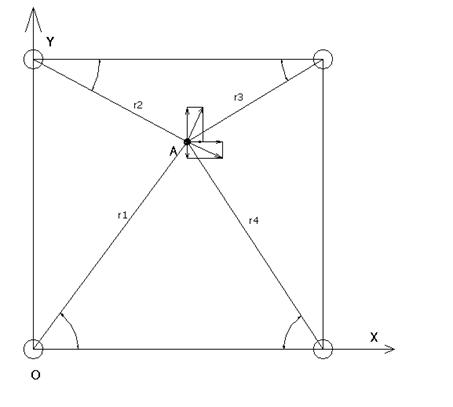
Шаг 2. Аналогично рассчитываем поле напряжений, создаваемое каждым из скважинных зарядов k_i в своих координатах (R_ki, φ, Z) с учётом времени замедления, точек инициирования и других особенностей i-го заряда. Затем пересчитываем напряжения от каждого из скважинных зарядов в единой системе координат (X,Y,Z) – (рис.2) и находим суммарные напряжения в этой системе координат.

Рис. 2 - Единая система координат для четырех зарядов

Шаг 3. После этого находим главные напряжения

В предыдущих методиках рассчитывались проекции напряжений на координатные оси. В данной методике был сделан переход к главным напряжениям, для более точной оценки влияния параметров поля напряжения на массив горных пород. Это позволяет напрямую оценивать зону разрушения по критерию максимальных растягивающих напряжений.

В трех мерном случае уравнения, отвечающие за преобразование координатных осей, будут иметь вид [5]:

где: x, y, z – первоначальные координатные оси, x', y', z'- новые координатные оси, l, m, n - направляющие косинусы между осями.

Для напряженного состояния существуют три взаимно перпендикулярные главные площадки, для которых составляющие нормального напряжения имеют стационарное значение (максимум, минимум или минимакс); компоненты же касательного напряжения в этих площадках равны нулю. Такие нормальные напряжения будут главными напряжениями.

Эти уравнения позволяют определить направляющие косинусы l, m, n для главных площадок. В силу равенства  величины l, m, n не могут одновременно обратиться в ноль. Уравнения являются однородными линейными уравнениями относительно l, m, n и дают решения, отличные от нуля в том случае, ели детерминант этих уравнений равен нулю. Вычисляя этот детерминант и приравнивая его к нулю, приходим к следующему кубическому уравнению относительно:

Данное уравнение решается методом половинного деления. Три корня этого уравнения дают значения трех главных напряжений.

Таким образом, получаем зависимости главных напряжений от времени для некоторой расчётной точки.

Шаг 4. Выбираем максимальные значения главных напряжений для этой точки иповторяем расчёт для точек в некотором выбранном сечении. Далее при выполнении всех расчетов, получаем распределение максимальных главных напряжений в выбранном сечении горного массива. Иными словами, сразу получаем картину разрушения породы в выбранном сечении по критерию максимальных растягивающих и сжимающих напряжений.

Разработанная методика реализована в программной среде PASCAL.

Исходные данные, необходимые для расчёта: длина заряда, м; теплота взрывчатого превращения ВВ, Дж; скорость детонации, м/с; координата верхнего конца заряда по оси Z, м; длина заряда, м; диаметр заряда, м; скорость продольной волны, м/с; скорость поперечной волны, м/с; плотность горной породы, кг/м³; координаты точки наблюдения А, количество зарядов, шт.; количество точек инициирования, шт.; координаты точек инициирования; время замедления при инициировании между зарядами и по заряду;

После проведения всех расчетов получаем численные данные формирования поля напряжения при заданных параметрах БВР.

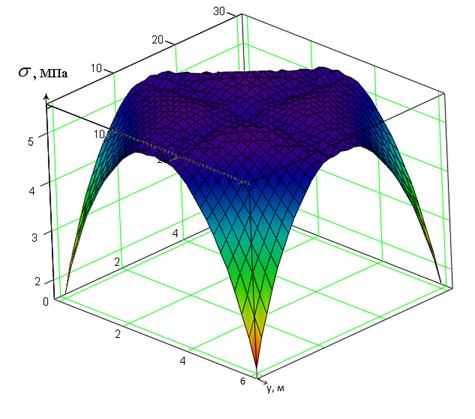
На рис. 3 представлено волновое поле напряжений при взрыве системы скважинных зарядов для условий карьера «Прудянский» месторождения Пруды-Моховое-Яскинское.

Рис. 3 - Волновое поле напряжений при взрыве скважинных зарядов.

Выводы:

1. Разработана методика расчета параметров волн напряжений, позволяющая численно смоделировать напряженное состояние массива от взрыва системы скважинных зарядов с учетом последовательности их инициирования.
2. Предложенная методика позволяет оценить влияние каждого из параметров БВР на формирование поля напряжений.
3. Данная методика прошла апробацию при производстве буровзрывных работ на карьере «Прудянский» месторождения Пруды-Моховое-Яскинское и результаты расчета  и опытных взрывов показали удовлетворительную сходимость.

Литература

1. Боровиков В.А., Ванягин И.Ф. К расчету параметров волны напряжения при взрыве удлиненного заряда в горных породах. Взрывное дело, Сб. 76/33, М., Недра, 1976.
2. Боровиков В.А., Ванягин И.Ф., Менжулин М.Г., Цирель С.В.. Волны напряжений в обводненном трещиноватом массиве./ Учебное пособие/Ленинград, 1989.
3. Ермолаев И.Ю. Автореферат на соискание уч. ст. к.т.н. дис., СПб, СПбГГИ (ТУ), 1992 г.
4. Стоянова Т.В., Управление интенсивностью процесса разрушения при отбойке гранита на щебень, Дис. К.т.н., СПб., СПГГИ, 1998 г.
5. Ван Цзи-де. Прикладная теория упругости. М., 1959 г.

References

1. Borovikov V.A.Vanyagin I.F. K raschetu parametrov volni napryajeniya pri vzrive udlinennogo zaryada v gornih porodah. Vzrivnoe delo SPb. 76/33 M. Nedra_ 1976.
2. Borovikov V.A. Vanyagin I.F. Menjulin M.G. Cirel S.V. Volni napryajenii v obvodnennom treschinovatom massive./Uchebnoe posobie/Leningrad 1989.
3. Ermolaev I.Y. Avtoreferat n asoiskanie uch. st.k.t.n. dis. SPb SPbGGI(TU), 1992 g.
4. Stoyanova T.V.Upravlenie intensivnostyu processa razrusheniya pri otboike granite na scheben Dis. K.t.n. SPb. SPGGI 1998 g.
5. Van Czi de.Prikladnaya teoriya uprugosti. M. 1959 g.