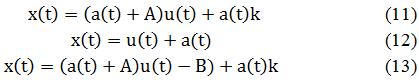METHODOLOGY AND ALGORITHM OF MATHEMATICAL ANALYSIS MULTIFACTOR MODELS OPTIMAL CONFIGURATION OF RENEWABLE ENERGY SOURCES

Гапоненко А.М.¹, Каграманова А.А.²

¹ Доктор технических наук, профессор, ² ORCID: 0000-0003-4069-4767, аспирант, Кубанский государственный технологический университет

МЕТОДИКА И АЛГОРИТМ МАТЕМАТИЧЕСКОГО АНАЛИЗА МНОГОФАКТОРНОЙ МОДЕЛИ ОПТИМАЛЬНОЙ КОНФИГУРАЦИИ НЕТРАДИЦИОННЫХ ВОЗОБНОВЛЯЕМЫХ ИСТОЧНИКОВ ЭНЕРГИИ

Аннотация

Рассмотрена имитационная модель гибридного кластера НВИЭ и определена структура функционала для показателей его эффективности. Предложен «пошаговый» подход к решению задачи нахождения экстремума функции отклика нелинейной модели полного факторного эксперимента.

Описан алгоритм математического анализа многофакторной модели для НВИЭ с учетом случайного характера динамических характеристик.

Предложен метод описания климатических процессов, учитывающий нестационарность их статистических свойств. Суть метода состоит в исключении из исследуемого процесса закономерностей и последующей оценке параметров случайной компоненты. Применение моделей нестационарных случайных процессов на практике позволит снизить неопределенность учета внешних факторов в задачах обоснования схем энергоснабжения на основе ВИЭ и повысить достоверность принимаемых решений.

Ключевые слова: возобновляемые источники энергии, гибридный энергетический кластер, многофакторная модель, математический анализ.

Gaponenko A.M.¹, Kagramanova A.A.²

¹PhD in Engineering, ²ORCID: 0000-0003-4069-4767, Postgraduate student, Kuban State Technological University

METHODOLOGY AND ALGORITHM OF MATHEMATICAL ANALYSIS MULTIFACTOR MODELS OPTIMAL CONFIGURATION OF RENEWABLE ENERGY SOURCES

Abstract

We consider the simulation model of hybrid renewable energy cluster, and determined the structure of functional for the performance of its effectiveness. Is offered a "step by step" approach to solving the problem of finding the extremum of the response function of the non-linear model of full factorial experiment. The algorithm of mathematical analysis multivariate model for renewable energy taking into account the random nature of the dynamic characteristics. The method of describing climatic processes, taking into account the nonstationarity of their statistical properties. The method consists in the elimination of investigational process regularities and subsequent measurement of parameters the random component. The use of models of nonstationary random processes in practice will reduce the uncertainty taking into account external factors in the problem of energy supply circuits based on renewable energy sources and improve the reliability of decisions.

Keywords: renewable sources of energy, hybrid energy cluster, multifactor model mathematical analysis.

Определим понятие гибридного кластера, как совокупность нетрадиционных возобновляемых источников энергии (НВИЭ).

Рассмотрим имитационную модель такого  кластера, следуя [1].  В самом общем виде ее можно представить функциональной зависимостью следующего вида [2]

,                                    (1)

где G_кл − показатель эффективности гибридного кластера; v − совокупность факторов воздействия внешней среды: скорость ветра (ВЭУ), инсоляция (ФЭП, СК), напор, расход (мГЭС), температура НПИ (ТН), режим метангенерации (БГУ); А, Е, S, М, F − тип кластера в зависимости от доли замещаемой мощности (кластеры: А − микро; Е − мини; S − малый; М − средний; F − полный); d, h, r, p, s, sp − тип кластера в зависимости от вида НВИЭ в системе:

• d − двойной гибрид (ДГ+ВЭУ или ДГ+ФЭП или ДГ+мГЭС и т.п.);
• h − трио-кластер (ДГ+ВЭУ+ФЭП или ДГ+ВЭУ+мГЭС);
• k − квадро-кластер (ДГ+ВЭУ+ФЭП+мГЭС);
• p − пента-кластер (ДГ+ВЭУ+ФЭП+мГЭС+ТН+БГУ);
• s − сикстет-кластер (ДГ+ВЭУ+ФЭП+мГЭС+ТН+БГУ);
• sp − септ-кластер (ДГ+ВЭУ+ФЭП+мГЭС+ТН+БГУ+СК);

СС_j − себестоимость производства 1 кВт∙ч разными видами НВИЭ;

U_j − стоимость кВт установленной мощности вида НВИЭ.

В общем виде объект исследования можно представить в виде структурной схемы, показанной на рис. 1.

Рассмотрение объекта в виде такой схемы основано на принципе «черного ящика», который имеет следующие группы параметров:

• Х_i − управляющие (входные), которые называются факторами;
• Y_i − выходные параметры, которые называются параметрами состояния;
• W_i − возмущающие воздействия.

 

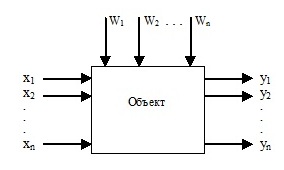
Рис. 1 – Структурная схема объекта исследования

Необходимо учесть, что возмущающие воздействия W_i не поддаются контролю, следовательно, являются случайными или меняющимися во времени (скорость ветра, инсоляция, температура воздуха, грунта, теплоносителя), из-за множества случайных возмущений, и задача идентификации для сложных объектов требует статистических методов для определения динамических характеристик.

Традиционно, для анализа технико-экономических характеристик НВИЭ, оценивающих влияние внешних климатических факторов применяют методы описательной статистики, которые сводятся к комбинированию двух основных подходов: 1) усреднения в пределах длительных интервалов времени, например, среднемесячные и среднегодовые значения; 2) использования статистических распределений, параметры которых также получены усреднением по времени, например, описание ветровых режимов распределением Вейбулла. Наряду с этим реальные геофизические процессы подвержены циклическим колебаниям как кратковременного (суточные циклы), так и долговременного характера (годовые циклы). Как правило, климатические данные представлены выборками небольшого объема. Эффективной заменой традиционных методов при малом времени реализации и наличии априорной информации о процессе могут служить параметрические методы, применяемые в радиофизике, экономических и социальных исследованиях [3-11].

Каждый фактор х_i имеет область определения, которая должна быть установлена до проведения эксперимента. Сочетание представленных факторов можно представить как точку в многомерном пространстве, описывающую состояние системы.

В реальных условиях цель многофакторного эксперимента заключается в установлении зависимости

                             (2)

описывающей поведение объекта. Как правило, функция (2) строится в виде полинома n-го порядка:

                            (3)

где х_i, x_k, x_ik − управляющие параметры, а_i, a_k, a_ik − соответствующие коэффициенты, описывающие вклад каждого управляющего параметра.

Построение зависимостей (2) в виде (3) при минимальном количестве измерений значений управляющих параметров, обеспечивающих достоверность описания является целью многофакторного эксперимента.

Известно, что оборудование на любом объекте, обеспечивающее его энергоэффективность имеет динамические характеристики. Следовательно, входные факторы и параметры объекта зависят от времени, что усложняет задачу, делая ее нестационарной.

Главная практическая задача заключается в определении оптимальных условий для исследуемого объекта. Как правило, при многофакторном эксперименте необходимо найти значения факторов х_i, х_k, х_i,k таких, при которых отклик системы принимает значения у_max или y_min. Таким образом, построенная целевая функция отклика (3) исследуется на экстремум  и задача оптимизации сводится к определению множества {х_{i опт}, х_{k опт}, х_{i,k опт}} управляющих параметров, обеспечивающих экстремум целевого функционала.

При этом на значения факторов накладываются дополнительные ограничения, диктуемые условиями эксплуатации гибридного кластера

                                  (4)

Таким образом, задачей оптимизации является нахождение экстремума функции отклика при условии, что сама функция априори неизвестна. Один из возможных вариантов: экстремум будет означать минимальную стоимость оборудования, входящего в рассматриваемый кластер НВИЭ, при минимальном сроке окупаемости комплекса при условии, что функционирование кластера обеспечивает необходимую потребляемую энергию.      В качестве критерия эффективности проектного решения можно принять критерий минимального разброса стоимости одного кВт∙ч отпускаемой кластером электроэнергии при заданном простом сроке окупаемости.

Эта задача может быть решена многими способами:

1. Посредством полного факторного эксперимента строится нелинейная модель функции отклика, и затем у этой функции находится экстремум. Такая модель может оказаться сложной и потребовать большого количества опытов, так как требования нахождения ее экстремума создают необходимость проведения полного факторного эксперимента в широком диапазоне варьирования и при большом числе опытов.
2. Наиболее практически приемлемым оказывается «пошаговый» подход к решению задачи нахождения экстремума. При этом эксперимент проводится в ограниченной области, то есть используется конкретный набор возмущающих воздействий W_i (скорость ветра, инсоляция). Определяется направление роста функции отклика (при нахождении максимума) или направление падения функции отклика (при нахождении минимума). Далее эксперимент проводится в следующей области и т.д. Таким образом, проводится последовательный поиск экстремума функции отклика. В этом случае задача оптимизации может быть решена без полного описания функции отклика во всей области варьирования факторов. Пошаговое движение происходит до падения функции в частный оптимум (экстремум функции в выбранном направлении).

В итоге пошагового движения обоими методами определяем квазистационарную область, близкую к точке оптимума. Эта область априори не может быть описана гиперплоскостью и требует описания в виде нелинейной модели (гиперболоида, параболоида и т.д.)

Определить оптимальную конфигурацию кластера НВИЭ для различных мощностей позволяет использование многофакторной модели.

Рассмотрим частный случай, когда один из источников энергии не зависит от случайных возмущений (например, работу дизеля). Назовем такой источник гарантированным. Работа оставшихся источников НВИЭ подвержена случайным возмущениям (например, использование ветровой и солнечной энергии). Такие источники назовем стахостическими.

Обозначим: a − количество электроэнергии, вырабатываемое кластером (в единицу времени); b − допустимый уровень средней стоимости 1 кВт∙ч, вырабатываемого кластером; r₀ − стоимость эксплуатации гарантированного источника за единицу времени (содержится как стоимость оборудования, так и стоимость обслуживания); r_k − стоимость эксплуатации в течение часа  k-типа оборудования из остальных стахостических источников; g₀ − доля (от a), вырабатываемая гарантированного источником; g_k − доля (от a), вырабатываемая k- стахостическим источником.

Измеряемые случайные величины: Z_k − количество энергии, вырабатываемой за единицу времени k- стахостическим источником.

Пусть для каждой из случайных величин  Z_k имеется выборка из N наблюдений.

Вычисляемые (по выборке для Z_k) случайные величины:

                                (5)

где Y_k − стоимость энергии, произведенного k- стахостическим источником в единицу времени.

Далее получим для каждой из случайных величин Y_k выборку, также состоящую из N наблюдений:

                          (6)

где Y/a − стоимость энергии, вырабатываемой кластером за единицу времени (это случайная величина, тогда как первое слагаемое в правой части − неслучайно).

Находим для Y_k по выборкам: m_k − средняя стоимость энергии, вырабатываемой k-источником за единицу времени (выборочное среднее по Y_k); m₂ − средняя стоимость 1 кВт∙ч, вырабатываемого солнцем (выборочное среднее по Y₂);

                          (7)

где m − средняя стоимость энергии, вырабатываемой кластером за единицу времени; b − допустимый уровень средней стоимости 1 кВт∙ч, вырабатываемого кластером (b<r₀).

Для объективного учета возмущающих воздействий, основным свойством которых является нестационарный случайный характер необходимо применять методы анализа нестационарных случайных процессов [12].

Следовательно, детерминирующую составляющую таких процессов можно описать функцией

                                             (8)

где Ф(t) − периодическая последовательность суточных колебаний; М, Ω, ? − амплитуда, частота и фазовый угол годовых колебаний.

Воздействие детерминированных факторов на случайный процесс в общем виде можно описать комбинацией аддитивной (9) и мультипликативной (10) моделей:

                                    (9)

                                                                                                                                                                                                            (10)

где u(t) − реализация стационарного случайного процесса; a(t) − детерминированная функция.

Исключив детерминированную составляющую, оставшуюся часть можно считать случайной компонентой. Статистические свойства случайной составляющей процесса можно оценить, используя традиционно применяемые методы теории вероятности и математической статистики.

После определения закономерностей их можно исключить из исследуемых процессов. На этом этапе необходимо выбрать параметры модели, комбинируя зависимости (8) и (9). Эффективность мультипликативной и аддитивной моделей в исследуемом случайном процессе можно оценить по косвенным признакам, характерным для этих двух типов моделей [4]. В результате были получены формулы (11, 12, 13), выражающие соотношения детерминированной и случайной компонент для процессов изменения интенсивности солнечного излучения, температуры наружного воздуха и скорости ветра соответственно.

где A, B, k − параметры моделей, определяющие соотношение детерминированной и случайной компоненты.

Остатки процессов изменения температуры наружного воздуха и интенсивности солнечного излучения хорошо описываются нормальным распределением. Распределение случайной компоненты изменений скорости ветра имеет асимметричную форму и с приемлемой точностью описывается функцией Вейбулла.

Выводы:

1. Рассмотрена имитационная модель гибридного кластера НВИЭ и определена структура функционала для показателей его эффективности.
2. Предложен «пошаговый» подход к решению задачи нахождения экстремума функции отклика нелинейной модели полного факторного эксперимента.
3. Описан алгоритм математического анализа многофакторной модели для НВИЭ с учетом случайного характера динамических характеристик.
4. Предложен метод описания климатических процессов, учитывающий нестационарность их статистических свойств. Суть метода состоит в исключении из исследуемого процесса закономерностей и последующей оценке параметров случайной компоненты. Применение моделей нестационарных случайных процессов на практике позволит снизить неопределенность учета внешних факторов в задачах обоснования схем энергоснабжения на основе ВИЭ и повысить достоверность принимаемых решений.

Литература

1. Велькин В.И., Логинов М. И. Выбор оптимального состава оборудования в кластере возобновляемых источников энергии на основе регрессионного анализа // Международный научный журнал «Альтернативная энергетика и экология». №03 (107). 2012. С. 100-104.
2. Гапоненко А. М., Каграманова А. А. Оптимизация состава комплекса возобновляемых источников энергии с использованием кластерного подхода и теории случайных процессов / Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета (Научный журнал КубГАУ) [Электронный ресурс]. – Краснодар: КубГАУ, 2016. – №02(116). С. 94 – 109. – IDA [article ID]: 1161602005. – Режим доступа: http://goo.gl/IfkmOL
3. Андерсон Т. Статический анализ временных рядов. М.: Мир, 1976.
4. Бендат Дж., Пирсол А. Прикладной анализ случайных данных: Пер. с англ. М.: Мир, 1989.
5. Бендат Дж., Пирсол А. Применение корреляционного анализа и спектрального анализа: Пер. с англ. М.: Мир, 1983.
6. Бокс ДЖ., Дженкинс Г. Анализ временных рядов. Прогноз и управление. М.: Мир, 1974.
7. Вентцель Е.С. Теория случайных процессов и ее инженерные приложения. Учеб. Пособие для втузов. 2-у изд., стер. М.: Высш. Шк., 2000.
8. Евланов Л.Г., Константинов В.М. Системы со случайными параметрами. М.: Наука, 1976.
9. Рытов С.М. Введение в статическую радиофизику. Ч.1. Случайные процессы. М.: Наука, 1976.
10. Рытов С.М. Модулированные колебания и волны // Труды Физ. Института АН СССР. 1940. Т. 2, вып. 1.
11. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере / Под ред. В.Э. Фигурнова. 3-е изд., перераб. И доп. М.: ИНФРА-М, 2003.
12. Щеклеин С.Е., Власов В.В. Моделирование нестационарных случайных процессов в задачах обоснования возобновляемых источников энергии // Международный научный журнал «Альтернативная энергетика и экология». №03 (107). 2012. С. 67-71.

References

1. Vel'kin V.I., Loginov M. I. Vybor optimal'nogo sostava oborudovanija v klastere vozobnovljaemyh istochnikov jenergii na osnove regressionnogo analiza // Mezhdunarodnyj nauchnyj zhurnal «Al'ternativnaja jenergetika i jekologija». №03 (107). 2012. S. 100-104.
2. Gaponenko A. M., Kagramanova A. A. Optimizacija sostava kompleksa vozobnovljaemyh istochnikov jenergii s ispol'zovaniem klasternogo podhoda i teorii sluchajnyh processov / Politematicheskij setevoj jelektronnyj nauchnyj zhurnal Kubanskogo gosudarstvennogo agrarnogo universiteta (Nauchnyj zhurnal KubGAU) [Jelektronnyj resurs]. – Krasnodar: KubGAU, 2016. – №02(116). S. 94 – 109. – IDA [article ID]: 1161602005. – Rezhim dostupa: http://goo.gl/IfkmOL
3. Anderson T. Staticheskij analiz vremennyh rjadov. M.: Mir, 1976.
4. Bendat Dzh., Pirsol A. Prikladnoj analiz sluchajnyh dannyh: Per. s angl. M.: Mir, 1989.
5. Bendat Dzh., Pirsol A. Primenenie korreljacionnogo analiza i spektral'nogo analiza: Per. s angl. M.: Mir, 1983.
6. Boks DZh., Dzhenkins G. Analiz vremennyh rjadov. Prognoz i upravlenie. M.: Mir, 1974.
7. Ventcel' E.S. Teorija sluchajnyh processov i ee inzhenernye prilozhenija. Ucheb. Posobie dlja vtuzov. 2-u izd., ster. M.: Vyssh. Shk., 2000.
8. Evlanov L.G., Konstantinov V.M. Sistemy so sluchajnymi parametrami. M.: Nauka, 1976.
9. Rytov S.M. Vvedenie v staticheskuju radiofiziku. Ch.1. Sluchajnye processy. M.: Nauka, 1976.
10. Rytov S.M. Modulirovannye kolebanija i volny // Trudy Fiz. Instituta AN SSSR. 1940. T. 2, vyp. 1.
11. Tjurin Ju.N., Makarov A.A. Analiz dannyh na komp'jutere / Pod red. V.Je. Figurnova. 3-e izd., pererab. I dop. M.: INFRA-M, 2003.
12. Shheklein S.E., Vlasov V.V. Modelirovanie nestacionarnyh sluchajnyh processov v zadachah obosnovanija vozobnovljaemyh istochnikov jenergii // Mezhdunarodnyj nauchnyj zhurnal «Al'ternativnaja jenergetika i jekologija». №03 (107). 2012. S. 67-71.