The power of the Charlier criterion for detecting outliers in construction work measurements

В строительной отрасли при выполнении различных работ осуществляется множество разнообразных измерений, направленных на контроль качества строительных процессов, характеристик качества строительных материалов, конструкций и изделий. Внедрение новых технологий, строительных материалов и изделий требует значительного повышения точности проводимых измерений и повышенных требований к обработке получаемых результатов. В этой связи большое значение имеет своевременное выявление грубых погрешностей или так называемых выбросов в данных, полученных при измерениях

Избежать появление промахов в процессе измерений можно в результате четкой организации измерений, качественной подготовкой операторов, настройки и своевременной поверки средств измерений. Однако, все это не гарантирует на 100 % отсутствие выбросов. Таким образом, основной задачей статистической обработки полученных результатов измерений является выявление и исключение выбросов из серии измерений.

Для выявления грубых погрешностей разработано достаточно большое количество критериев, позволяющих производить отсев аномальных измерений из серии проведенных измерений искомой величины. Эффективность таких критериев зависит от объема выборки

Грубые погрешности выявляют в самом начале статистической обработки измерений, на первом этапе. В зависимости от количества измерений используют такие статистические критерии как критерий Граббса

Мощность таких критериев и их сравнительный анализ достаточно хорошо описаны в открытой печати, например, в работе

В связи с этим возникла необходимость проверки эффективности критерия Шарлье в выборках большого и малого объема, что и является целью данной работы.

Проверка мощности критерия осуществлялась на основе методики, изложенной в работе

Эксперимент проводился на выборках с количеством измерений 5, 10, 20, 30, 40.

Суть методики

Вначале создается генеральная совокупность много большего объема, чем проверяемые выборки. При этом элементы такой «эталонной» генеральной совокупности подчиняются строго нормальному закону с вероятностью, равной 1. На рис. 1 представлена гистограмма такого распределения с математическим ожиданием mx= 25 и стандартным отклонением σ = 1.

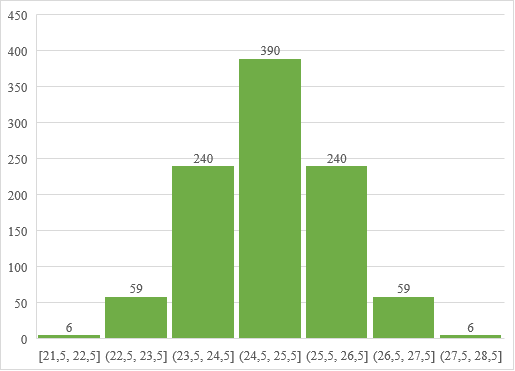
Рисунок 1 - Гистограмма генеральной совокупности

DOI:10.60797/IRJ.2025.154.27.1

Принимая во внимание правило 3-х сигм, можно полагать, что все значения случайной величины, имеющей нормальное распределение, будут находиться в границах (mx - 3σ, mx + 3σ) с вероятностью 99,7%, т.е. практически с доверительной вероятностью, равной 1. Необходимо отметить, что нужно отличать правило «трех сигм» и критерий «трех сигм», что не одно и то же. В первом случае задаются границы, внутри которых должна находиться случайная величина, используя параметры генеральной совокупности, т.е. математическое ожидание и стандартное отклонение. Во втором случае, когда речь идет о критерии «трех сигм», рассматривается интервал в границах (), полученный в результате статистической обработки выборок ограниченного объема. Если полученное при измерении значение измеряемой величины находится за границами (mx - 3 σ, mx + 3 σ), то с вероятностью 99,7% можно утверждать, что это – промах. Однако аналогичный вывод в отношении вероятности будет неправомерен в случае, если результат измерения выходит за границы интервала . Это связано с тем, что точечные оценки ограниченной выборки  и параметры mx, σ генеральной совокупности это – не одно и то же.

Далее из созданной «эталонной» генеральной совокупности извлекаются выборки определенного объема. При проведении теоретического эксперимента для извлечения выборок использовался online-генератор случайных чисел. Для каждого исследуемого объема выборок использовалось по 50 выборочных совокупностей. При этом изначально каждая случайная выборка была свободна от выбросов. Затем производится постепенное увеличение максимального значения в каждой выборке и одновременно выполняется проверка этого значения на выброс по критерию Шарлье. Для удобства проверки очередного значения измеряемой величины на промах методикой предусмотрено формирование нормированного отклонения xнорм = (xmax - mx)/ σ, т.е. если xнорм ≥ 3, то xmax будут являться промахами.

Условие xнорм = 3 будет являться граничным при единичной проверке мощности критерия Шарлье при выявлении выброса. Это значит, что, если при xнорм ≥ 3, критерий обнаружил промах, а при xнорм < 3 проверяемое значение не является промахом, то единичная проверка является успешной.

И наоборот, если при h ≥ 3 критерий Шарлье не обнаружит выброс, то единичная проверка не будет считаться успешной, а будет трактоваться, как ошибка второго рода, при этом количество успешных проверок будет являться характеристикой мощности критерия. Если проверяемое значение xmax < 3, то критерий определяет xmaxкак промах и это уже будет ошибкой первого рода.

При определении мощности критерия Шарлье был проведен статистический эксперимент, который заключался в моделировании измерений, не используя экспериментальные данные. Исследовались выборки объема при n = 5; 10; 20, 30, 40.

В соответствии с методикой

Далее на следующем этапе методики из генеральной совокупности извлекались выборки объемом n = 5. Извлечение производилось случайным образом с помощью online-генератора случайных чисел. Количество выборок определялось из условия обеспечения достаточной точности результатов дальнейших вычислений. В данной работе использовалось по пятьдесят выборочных совокупностей для каждого исследуемого объема выборки. Выборки производились в диапазоне (mx - 2σ, mx + 2σ), в котором находится более 95% значений генеральной совокупности. Максимальное значение выборки xmax принималось равным 27 (нормированное отклонение xнорм = 2) и проверялось на промах по критерию Шарлье. Выбросом в этом случае считается то значение измеряемой величины, для которого выполняется следующее неравенство

где, xк – проверяемое значение, – среднее арифметическое значение измеряемой величины, Sx – стандартное отклонение.

При нормированном отклонении h = 2 в пятидесяти выборках при проверке выбросов не было обнаружено, все единичные проверки были успешными при всех уровнях значимости. Таким образом, мощность критерия

(1)

где F(xнором) – количество успешных единичных проверок, N(xнорм) – общее количество единичных проверок.

Затем xmax увеличивалось до 27,2, в этом случае нормированное отклонение xнорм равнялось 2,2. После извлечения случайным образом выборки из генеральной совокупности производилась проверка максимального значения xmax = 27,2 на выброс, которая показала отсутствие промаха. Таким же образом проводились аналогичные проверки на выбросы в оставшихся сорока девяти выборках, извлекаемых также случайным образом из генеральной совокупности. После того как были проведены все единичные проверки на промах при нормированном отклонении xнорм = 2,2, подсчитывалось количество успешных проверок и определялась мощность критерия по формуле (1), которая составила 30%.

Аналогичным образом проводились проверки на выброс максимальных значений xmax, равных 27,4; 27,8; 27,9 т. е. при нормированных отклонениях xнорм, равных соответственно 2,4; 2,8; 2,9. Для максимальных значений, равных двадцати восьми и более, т. е. при xнорм ≥ 3, шаг изменения был увеличен до 1.

Для каждого значения нормированного отклонения xнорм подсчитывалось общее количество N (xнорм) единичных проверок и количество F (xнорм) удачных единичных проверок и определялась мощность критерия.

В таблицу 1 занесены полученные значения мощности критерия Шарлье P(xнорм) в зависимости от величины нормированного отклонения xнорм и объема выборки, а также данные, полученные из открытых источников

При графической интерпретации полученных результатов статистического эксперимента принимался во внимание тот факт, что точка xнорм = 3 при графическом изображении зависимостей P(xнорм ) является точкой разрыва. В этом случае точка xнорм = 3 для диапазона xнорм < 3 рассматривалась как 2,99.

Анализируя полученные результаты теоретического эксперимента, было произведено сравнение мощности критерия Шарлье с данными работ

Установлено, что на всем участке xнорм < 3 в выборках n= 5, 10, 20 мощность критерия Шарлье значительно меньше мощности критериев Романовского и Диксона (рис.2) при всех уровнях значимости (данных по мощности критерия Диксона при n = 30 и 40 в открытых источниках не было обнаружено, а критерий Романовского при числе измерений больше 20 не используется).

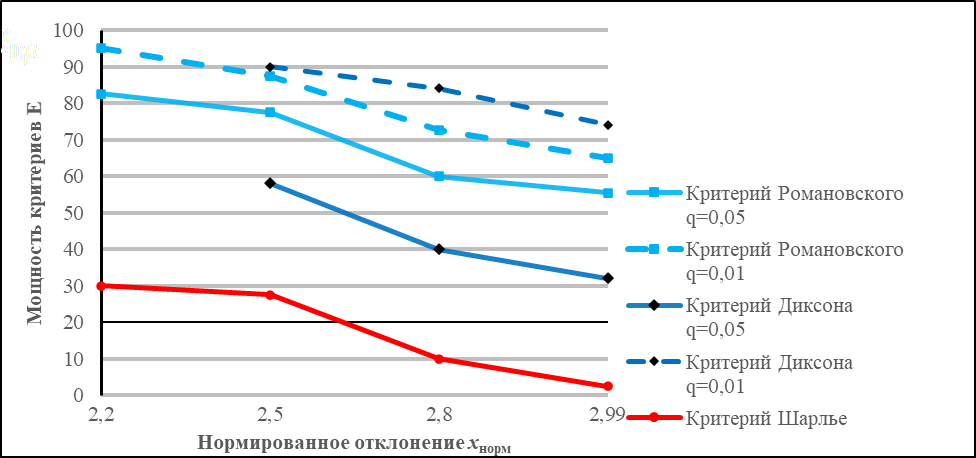
Рисунок 2 - Зависимость мощности критерия Шарлье от нормированного отклонения при n = 5

DOI:10.60797/IRJ.2025.154.27.3

На рис. 3 представлена зависимость критерия Шарлье от объема выборки при нормированном отклонении xнорм = 2,5.

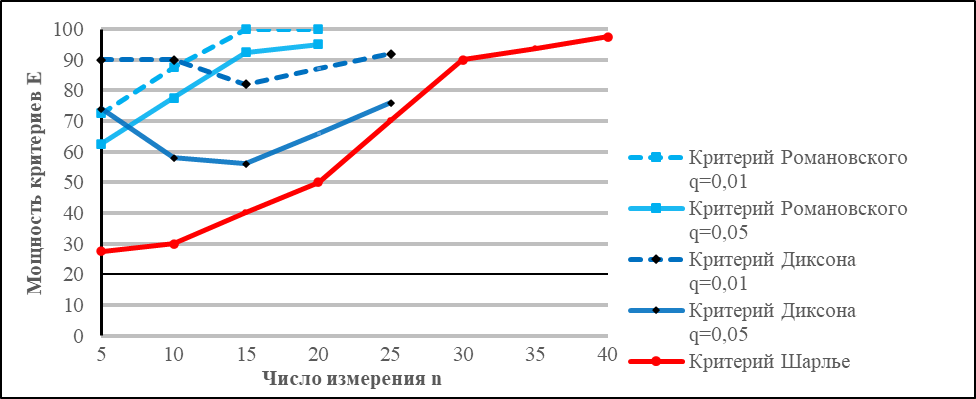
Рисунок 3 - Зависимость мощности критерия Шарлье от числа измерений n при нормированном отклонении xнорм = 2,5

DOI:10.60797/IRJ.2025.154.27.4

При нормированном отклонении в области h ≥ 3 мощность критерия Шарлье превышает P(xнорм, q) критериев Романовского и Диксона при всех объемах выборок и достигает 100% в выборках n = 30 и 40 уже при нормированном значении xнорм = 3,2, а в выборках n = 5, 10, 20 – при xнорм = 3,4. Это свидетельствует о том, что при использовании критерия Шарлье возникновение ошибки второго рода менее вероятно, чем при использовании критериев Романовского и Диксона. При этом ошибка второго рода (принятие ошибочной нулевой гипотезы, т.е. пропуск промаха) более опасна, чем ошибка первого рода (признание промахом наблюдение, которое промахом не является).

В области xнорм < 3 эффективность критерия Шарлье в выборках малого объема n = 5, 10, 20 не велика и составляет 30-40%, что значительно ниже мощности критериев Романовского и Диксона.

Таким образом, анализ полученных результатов теоретического эксперимента показывает, что критерий Шарлье обладает достаточной мощностью при выявлении выбросов только в выборках объемом более 20. А в выборках малого объема он надежен только при нормированном значении xнорм > 3, т.е. позволяет эффективно выявлять ошибки второго рода.

Проведенные исследования, выполненные в рамках теоретического эксперимента, позволили установить, что критерий Шарлье надежен во всех диапазонах нормированных значений в выборках с числом измерений, больше 20. При числе измерений 20 и менее данный критерий эффективен при выявлении ошибок второго рода, т.е. при нормированных значениях xнорм > 3, а при xнорм < 3 его мощность невысока и составляет 30-40%. В этом случае вероятность признания промахом наблюдения, которое промахом не является, очень высока, что не позволяет рекомендовать его к использованию на практике для выявления выбросов в данном диапазоне.

Таким образом, критерий Шарлье может быть использован при выявлении выбросов в выборках объемом более 20 наблюдений. В выборках малого объема (n≤ 20) он может быть рекомендован к совместному использованию с критериями Романовского и Диксона для выявления выбросов в диапазоне xнорм > 3, т.е. только для обнаружения ошибок второго рода.