A STUDY OF THE PROCESSES OF MOVING AND LONGITUDINAL MANOEUVRING OF A QUANTOMOBILE
A STUDY OF THE PROCESSES OF MOVING AND LONGITUDINAL MANOEUVRING OF A QUANTOMOBILE
Abstract
The aim of the computational study was to evaluate the dynamics and stability of the quantomobile at the stages of moving and longitudinal manoeuvring. Quantomobile is defined as a ground vehicle with a hypothetical quantum engine (QE) providing the crew with a tractive force (thrust) directly applied to its body. Methods include examining the balance of forces and moments and forming a dynamic Simulink model of the longitudinal motion of the quantomobile. The model takes into account the influence on the longitudinal stability of the position of the centre of application of the QE trust to the car body, the size of the trust and its inclination, rolling resistance of the support wheels, rest friction factors of the support wheels, aerodynamics of the car body, and others.
The results of the calculations made it possible to evaluate the speed dynamics of the crew together with the dynamics of changes in longitudinal overturning and stabilizing compensating moments at the stages of moving and longitudinal manoeuvring of the crew. The identified regularities formed the basis for design recommendations.
The longitudinal unbalance of a quantomobile and a conventional car in the moving and manoeuvring phases are significantly different. Placement of the trust over the supporting surface results in pitching moments that manifest themselves differently under different conditions. To neutralize the overturning moments in moving and manoeuvring modes, additional trasters are required, which are covered by a single control system with the main QE. The model as a whole can serve both as a means of working out design schemes of quantomobiles and as an operational solver of additional stabilizing trusters on board of a quantomobile. Due to the lack of information about similar conceptual studies of a hypothetical quantomobile, the novelty of the work can be deemed significant.
1. Введение
Начиная с Дирака , в физике развиваются идеи извлечения энергии из физического вакуума (ФВ) , , , . На базе этих идей рассматриваются концепции квантовых двигателей (КД) , . И хотя получаемые импульсы траста (тяги) КД пока малы, надежда на практическую реализацию названых идей становится все более существенной .
Предположение, что физики задачу извлечения энергии ФВ решат успешно, а инженеры создадут конструкции КД, инициирует необходимость рассмотрения особенностей использования этого траста для движения транспортного средства (ТС).
КД по схеме воздействия на экипаж напоминает реактивный двигатель (РД). Однако в случае РД траст создается как реакция на импульс отбрасываемой массы отработавших газов, получая эту массу газов в качестве опоры. В случае же КД траст создается за счет деформации поля ФВ (пронизывающего и рабочую камеру КД, и окружающую окрестность и составляющего единое целое). Опора трасту обеспечивается наружной частью фрагмента поля, что представлено в трудах Леонова В.С. , . Функционал рабочей камеры КД заключается в создании деформации пространства-времени, обеспечивающего за счет появляющегося градиента сил возникновение направленного траста.
Поскольку ориентированный траст КД непосредственно движет экипажем, трансмиссия становится ненужной, совокупность колес экипажа теряет функцию движителя – они остаются лишь опорными, ведомыми; трансмиссию можно изъять из конструкции ТС . Вывешенный над опорной поверхностью (ОП) траст меняет схему сил и моментов, используемую для традиционного автомобиля. Точки возникновения сил тяги в пятнах контакта ведущих колес автомобилей переносятся в точки приложения вектора тяги КД к корпусу ТС , , , .
При возможности переводить вектор траста в наклонное положение можно за счет вертикальной составляющей этого вектора осуществлять прижим экипажа к ОП, либо его вывешивание (вплоть до отлета от ОП). Это видоизменяет схему сил и моментов традиционных наземных ТС .
Вывешивание (лифт) может привести к реализации режимов летательного аппарата (ЛА). Реализация прижимающей силы (антилифт) при входе экипажа в воду может позволить даже реализацию режима подводной лодки (ПЛ). Это приводит к идее всесредного мультимодального квантомобиля (ВМК) , . Часть из режимов ВМК отражена в работе . Однако требуется значительная работа по заполнению совокупности априорных пока знаний по затрагиваемой проблеме.
Разница в величинах динамических нагрузок на колеса передней и задней осей экипажа, с точки зрения сохранения продольной устойчивости, для автомобиля имеет второстепенное значение – поскольку на его эксплуатационных режимах названые нагрузки воспринимаются встречными нормальными реакциями твердой ОП. В случае квантомобиля, однако, во-первых, при векторе траста, вывешенном над ОП, следует ожидать формирования значительного опрокидывающего момента (ОМ). Во-вторых, каким бы ни был этот ОМ, в отсутствие твердой опоры экипаж подвергнется вращательному движению в плоскости тангажа , , .
Оперативная нейтрализация ОМ для квантомобиля становится актуальной.
Эта актуальность заостряется на ОП с высоким сопротивлением качению (ОПВСК), особенно на режимах трогания и маневрирования ТС с КД.
Несмотря на второстепенность учета аэродинамических сил в формировании ОМ при троганиях и маневрах (по причине низких скоростей квантомобиля Vq в этих фазах), все же используем современный подход с привлечением статистики испытаний плохообтекаемых тел (ПОТ) (bluff bodies) , . В качестве эталонного тела, ввиду предпочтительности рассмотрения движения по ОПВСК, выбран ПОТ 1-Box, соответствующий автомобилю КамАЗ-4326 , (рис. 1). В расчетах использованы конструктивные данные именно по этому грузовику.
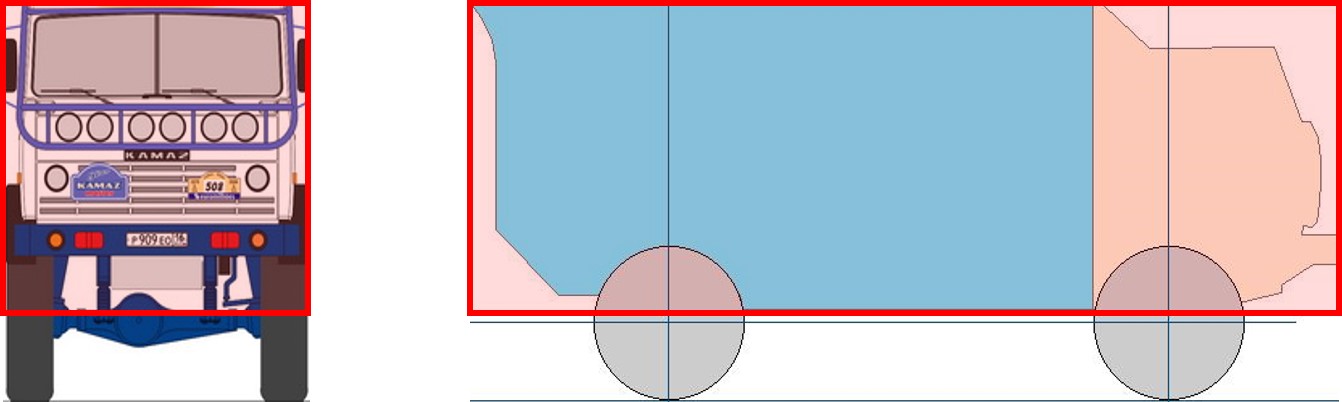
Рисунок 1 - Профили грузовика КамАЗ-4326 и ПОТ 1-Box
ПОТ 1-Box,вместе с тем, может корреспондировать с множеством наземных машин: других грузовиков, мобильных контейнеров, строительно-дорожных машин, других средств, для которых главным является взаимодействие с ОПВСК. И поскольку вопросы эргономики (с неясными пока экологическими свойствами КД) здесь не стоят, допустим в качестве объекта исследования беспилотное ТС – дающее возможность установки КД (и основного, и дополнительных, корректирующих) в любом месте пространства этого ТС.
2. Методы и принципы исследования
2.1. Цель и задачи исследования
Целью расчетного исследования явилась оценка динамики и устойчивости квантомобиля на этапах его трогания и продольного маневрирования, главным образом, на ОПВСК.
Устранение трансмиссии, перенос движительных функций с опорных колес на траст КД, способность вектора траста действовать в плоскости тангажа, появление возможности осуществлять лифт и антилифт квантомобиля – всё это, в отсутствие признанных теоретических основ движения квантомобиля и эмпирических данных, вызывает необходимость использовать подход с опорой на программное имитационное моделирование (ПИМ).
Задачами по достижению цели являются:
1) формирование математической модели продольного движения квантомобиля (МПДК) под поставленную цель;
2) построение Simulink-модели движения квантомобиля с детализацией трения покоя опорных колес, с отработкой интерфейса взаимодействия с моделью и вывода данных;
3) на базе Simulink-модели проведение ПИМ с экспериментами, охватывающими обоснованное множество вариантов движения;
4) обсуждение и обобщение результатов расчетов;
5) формирование рекомендаций и выводов.
2.2. Вектор траста и особенности его использования в МПДК
В рамках продольного движения экипажа в плоскости развёртывания угла тангажа β (см. рис. 2) вектор траста FT раскладывается на две ортогональные компоненты FTx и FTz , :
В скалярной записи это:
Угол наклона вектора FT
На рис. 2 квадрант I условно соответствует положительному направлению продольной тяговой силы, а квадрант II – отрицательному.
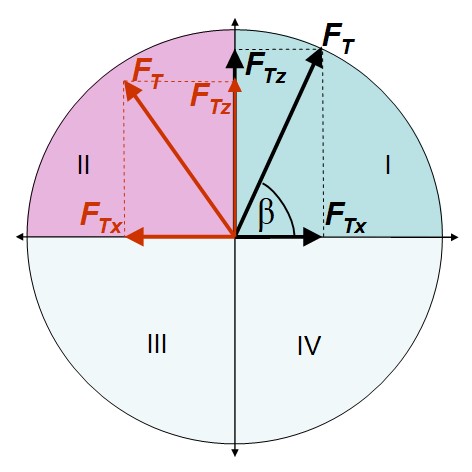
Рисунок 2 - Разложение вектора траста FT на горизонтальную FTx и вертикальную FTz компоненты
Примечание: β – угол наклона вектора FT относительно горизонта
2.3. Силовой баланс квантомобиля
В качестве основы модели движения экипажа по горизонтальной ОП выбран следующий вариант уравнения баланса горизонтальных сил квантомобиля :
где FTx – продольная сила тяги КвД (траст), Н;
Fr – сила сопротивления качению ведомых опорных колес, Н;
Fwx – сила сопротивления воздуха продольному движению (drag), Н;
Fa – сила инерции, противодействующая ускорению экипажа, Н;
Gq' – сила давления экипажа на ОП с учетом общего лифта, Н;
fk0 – коэффициент сопротивления качению колес при нулевой скорости;
fkv – скоростной коэффициент сопротивления качению колес, с2/м2;
cd – коэффициент аэродинамического сопротивления, безразмерный;
ρw – плотность воздуха, Н ×с2/м4;
Sfr – лобовая площадь экипажа, м2;
Gq – исходный вес (сила тяжести) квантомобиля, Н;
g – ускорение свободного падения, м/с2;
a – продольное ускорение экипажа, м/с2;
δwh – коэффициент инерции вращения опорных (ведомых) колес экипажа.
Сила Gq' = Gq – FTz – Fwz. Для квантомобиля приведенная масса m’ = Gq(1+δwh)/g учитывает вращение только опорных колес, поскольку вращающиеся детали традиционного силового привода отсутствуют.
Отметим, что Fr = Fk0 + Frv, где Fk0 = fk0 · Gq', а Frv = fk0 · frv ·Vq2· Gq'.
График прикладываемых к экипажу сил отображен на рис. 3. Обозначены: Vq – вектор скорости движения квантомобиля; V∞ – скорость невозмущенного набегающего потока воздуха (|Vq| = |V∞| в отсутствие ветра); Cg – центр тяжести (ЦТ) экипажа; Gq – сила тяжести экипажа; Fa – приведенная сила инерции экипажа; CFT – точка приложения траста КД к корпусу экипажа; FT, FTx и FTz, – сила тяги КвД (траст) и ее покоординатные компоненты; Cw – центр давления (ЦД) аэродинамических сил; Fw, Fwx и Fwz – сила воздействия воздуха и ее покоординатные компоненты; Ff1 и Ff2 – силы сопротивления качению передних и задних колес, соответственно; Tf1 и Tf2 – моменты сопротивления качению колес; hFwx, hFTx, hg – расстояния векторов соответствующих сил Fwx, FTx, Fa от ОП; lFwz, lFTz – расстояния векторов соответствующих сил Fwz, FTz до вертикали от оси задних колес; l0 – расстояние вектора силы Fwz до вертикали центра колесной базы; Lwb, L1 и L2 – расстояния базовое и от осей колес до проекции центра тяжести на ОП; A и B – центральные точки пятен контакта колес с ОП; Rz1 и Rz2 – нормальные реакции ОП.
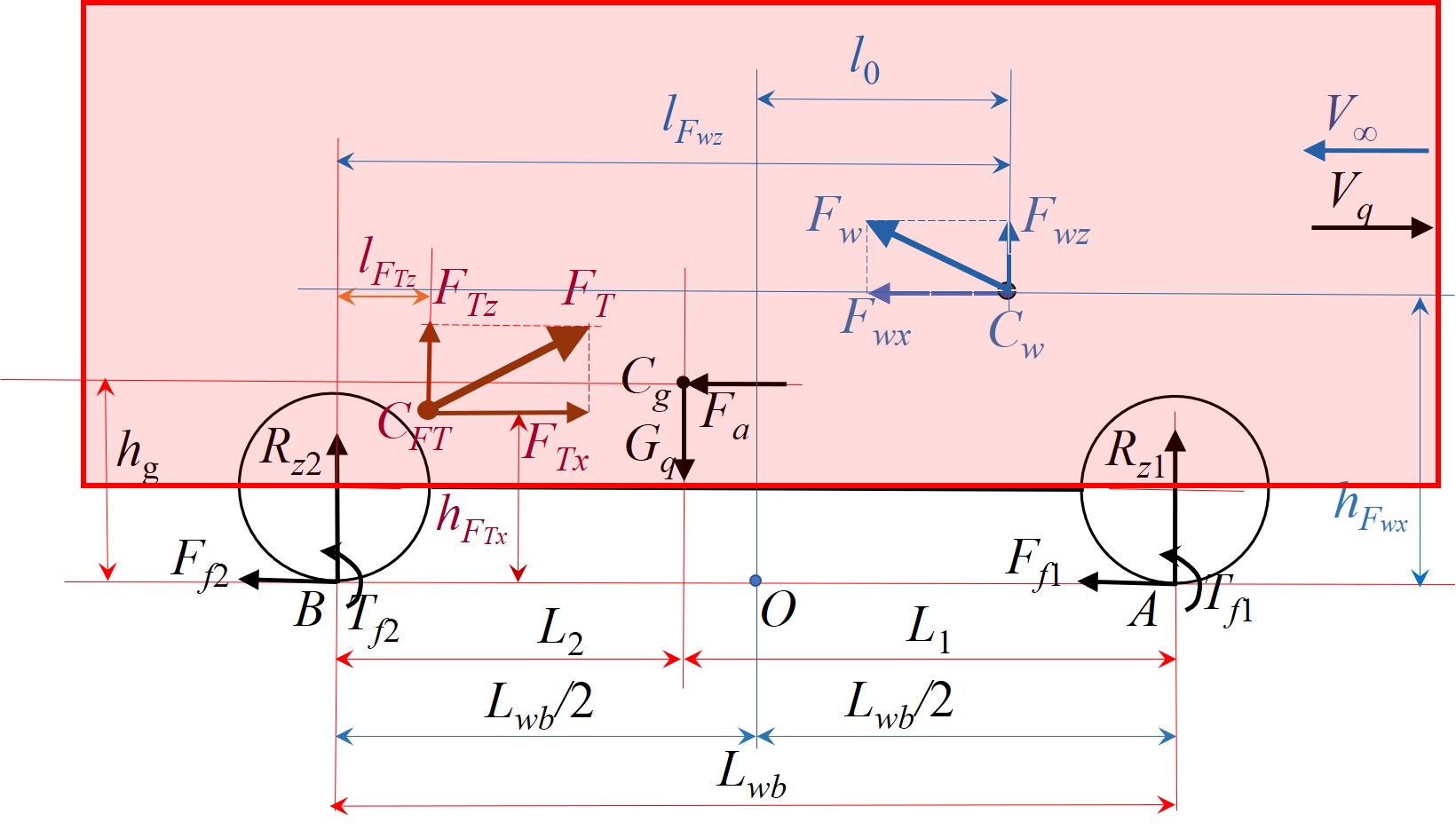
Рисунок 3 - Схема сил, действующих на квантомобиль
Примечание: форма кузова –1-Box [17], [18]
Силы воздействия воздуха Fwx и Fwz определяются с привлечением коэффициентов драга (cd) и лифта (cl) , .
2.4. Баланс моментов сил, действующих на квантомобиль
Баланс моментов сил детально рассмотрен в работе . Приведем главное. Если начало связанной плоской системы координат разместить в точке B (назовем её СКB – c осью x по направлению к передку экипажа, осью z вверх; положительными моментами – против часовой стрелки), то сумма всех моментов относительно точки B [13] (см. рис. 3):
Отметим, что сумма моментов (относительно точки B) определяет величину аэродинамического питч-момента (АПМ) и определенным образом связана с эмпирическим коэффициентом АПМ cm (определяемым экспериментально на базе баланса моментов относительно точки O (см. рис. 3)). Этому уделено внимание в авторских работах , , и ввиду малых скоростей рассматриваемых фаз движения детализация связи может быть обойдена (например, путем зануления в исходных данных коэффициентов cl и сm).
Из уравнения (5) можно найти нормальную реакцию ОП Rz1.
Подобное уравнение относительно точки A позволяет найти реакцию Rz2. Опрокидывающий питч-момент MΣpm = Lwb(Rz1–Rz2)/2. В статической постановке, если принять Rz2 = – Rz1, можно записать MΣpm = LwbRz1.
Требуемый стабилизирующий момент (ТСМ) тогда равен Mst = –MΣpm. Для оценки значимости АПМ MFw = MFwx + MFwz относительно ТСМ Mst введен коэффициент .
2.5. Трение покоя колес при трогании и смене направления продольного возвратно-поступательного движения экипажа
Процесс трогания ведомого колеса подобен картине сухого трения . Рассматриваем процесс без учета упругости и податливости элементов квантомобиля и ОП, а также скольжения колес – это позволяет линеаризовать модель трогания.
Чтобы вызвать качение ведомого колеса, к нему должно быть приложено толкающее усилие Fkx, необходимое для преодоления силы сопротивления сдвига покоящегося колеса. Для всех колес суммарно это: . Пока не достигнута эта величина – экипаж стоит (подвеска – условно жесткая). С другой стороны, в конце замедления ТС значение Fr в момент остановки сбрасывается с величины Fk0 до нуля.
Если экипаж меняет направление продольного движения на противоположное (и скорость проходит точку Vx = 0), то в момент остановки значение Fr сбрасывается до нуля, а затем наращивается до силы другого знака: –Fk0. Темп наращивания этой силы, а также момент страгивания колес зависит от величины тяговой силы FTx в этот период: при |FTx| ≥ |Fk0| движение колес (и экипажа) с наращиванием скорости начинается сразу, а при |FTx| < |Fk0| движение колес отсутствует до момента выполнения равенства |FTx| = |Fk0|. В алгоритме реализовано задействование сил Fr, Fk0 и FTx в условиях асинхронного изменения знака скорости.
2.6. Simulink-модель приземного движения квантомобиля (МПДК)
Структура имитационной системы состоит из четырех подсистем: Scenario – для формирования сценария исследования; расчета показателей динамики движения экипажа; расчета показателей энергетики; расчета нормальных реакций. Две базовые подсистемы МПДК: продольной динамики экипажа (Vehicle Dynamics), а также расчета нормальных реакций и питч-моментов (NormReactions) – представлены в авторских работах , .
Подсистемы оснащены множеством блоков визуализации. В подсистеме NormReactions, например, выходная информация собирается на 18-канальный осциллограф (распечатку выхода с него, например, см. ниже на рис. 4а и 7а).
3. Основные результаты
3.1. Подготовка и план расчетов
С целью количественной оценки динамики и продольной устойчивости квантомобиля посредством МПДК план расчетов охватил трогания и возвратно-поступательное маневрирование ТС, главным образом на ОПВСК.
Опорными значениями параметров выбраны данные автомобиля-прототипа КамАЗ-5326. При этом виртуально удалили из конструкции элементы трансмиссии и загладили днище – чем обеспечили снижение веса экипажа с 10 т до 8,8 т, а также условно обеспечили уровень cd = 0,32 (соответствующий выкладкам работы [18] для 1-Box). Задаваемые опорные параметры модели (см. ( 4)): Gq = 88000 Н; Lwb = 4,25 м; Sfr = 8,415 м2; hFTx = 1 м; lFTz=0,5 м; δwh = 0,04; fk0 = 0,3; fkv = 0,00037 с2/м2; cd = 0,32; cl = 0; cm= 0; ρw = 1,225 Н×с2/м4; g = 9,81 м/с2; β = 0º. Максимальное значение траста FT = 90000 Н: при угле β = 77,9º (максимальном в серии проведенных экспериментов ПИМ) оно обеспечивает полное вывешивание экипажа весом 88000 Н, оставляя FTx = 18865 Н на обеспечение горизонтального движения (в соответствии с (2) и (3), см. также детализированное обоснование в работах , ).
3.2. Трогание экипажа
Серия расчетов охватила перебор значений параметров: hFTx, lFTz, fk0, β – каждый, как правило, на 6 уровнях. Базовыми значениями явились hFTx = 1 м; lFTz = 0,5 м; fk0 = 0,3; сd = 0.32; β = 0º. На рис. 4a приведена распечатка результатов по базовому варианту максимально интенсивного трогания. Первая секунда затрачивается на рост FTx до значения 90000 Н, на второй секунде он остается на этом уровне. На рис. 4б – динамика изменения силы сопротивления качению Fr при различных углах наклона β вектора траста FT.
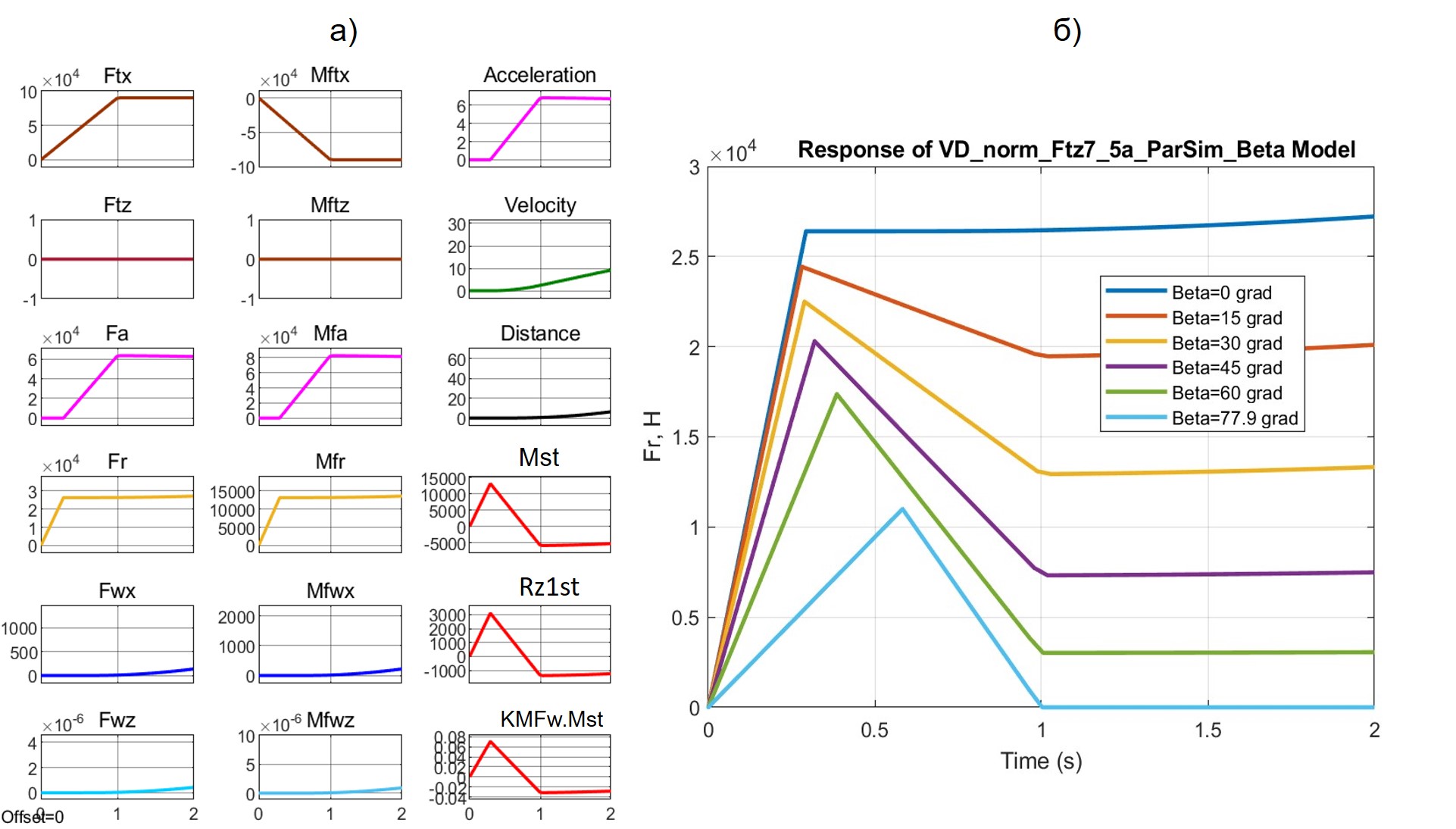
Рисунок 4 - Динамика изменения сил и моментов при трогании квантомобиля:
a) графики изменения показателей движения (при базовых значениях параметров); б) изменения силы Fr при различных углах β вектора траста FT
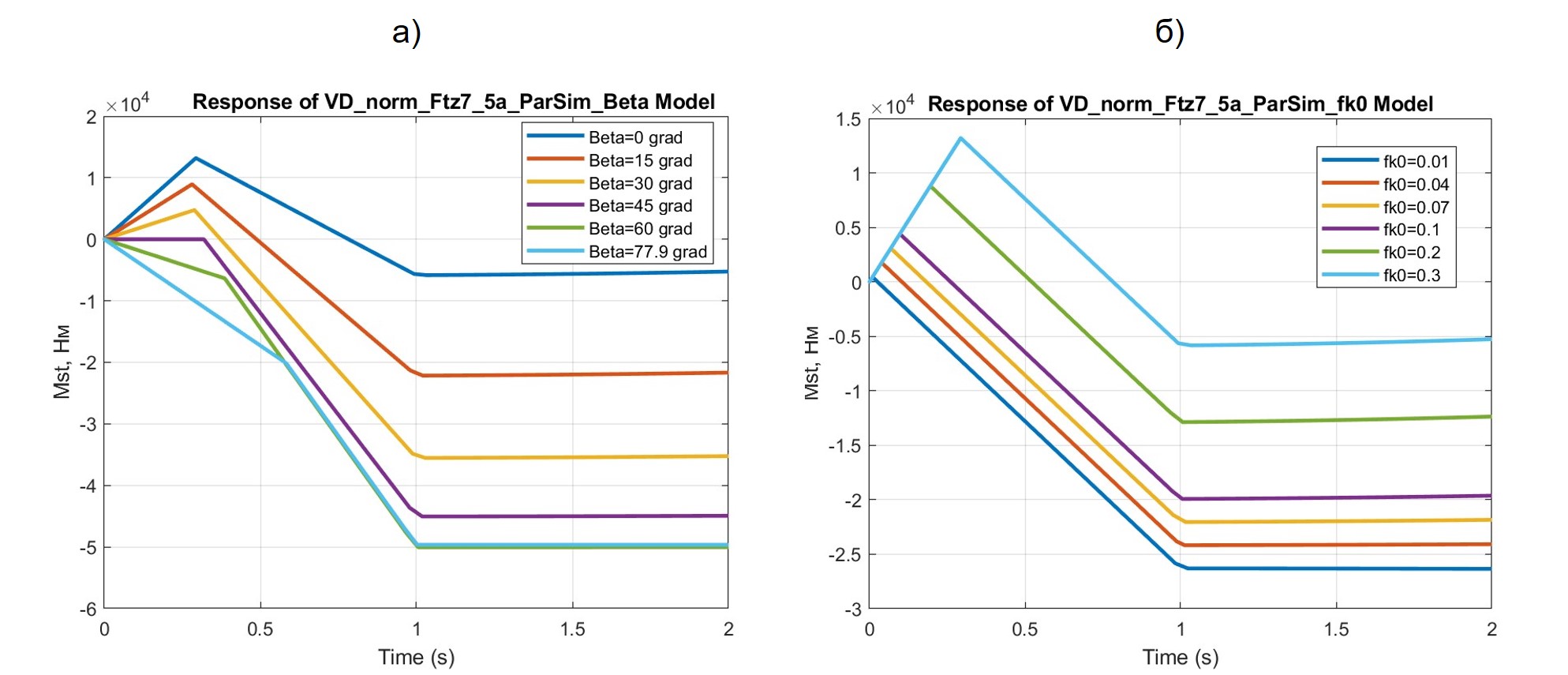
Рисунок 5 - Результаты расчетов процесса изменения ТСМ Mst при различных значениях β (а) и значениях fk0 (б)
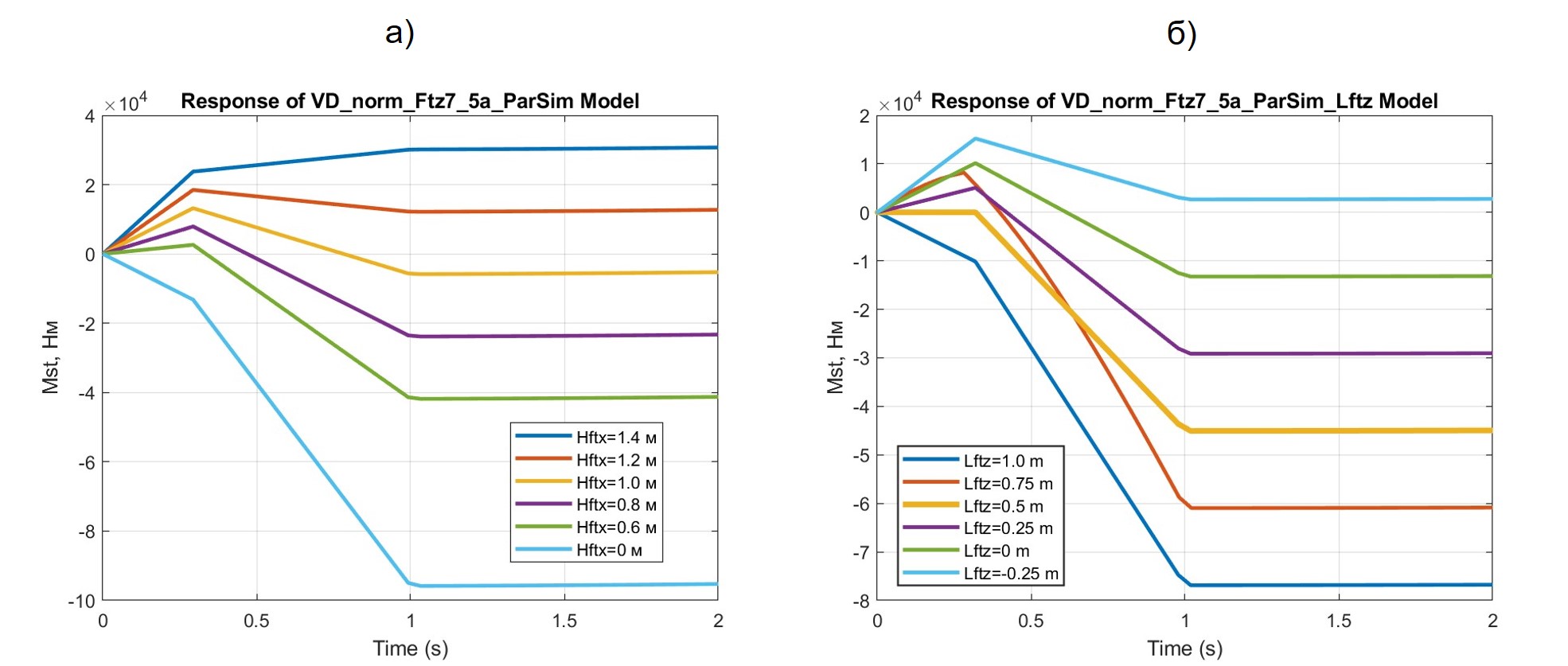
Рисунок 6 - Результаты расчетов процесса изменения ТСМ Mst при различных значениях hFTx (а) и lFTz (б)
Продольное маневрирование – здесь возвратно-поступательное движение экипажа путем знакопеременной смены направления компоненты FTx задающего вектора траста.
Воспользуемся для анализа возможностями графического вывода пакета МПДК. Отметим разницу в задании темпа изменения траста FTx: если в случае исследования троганий (рис. 4÷6) темп был максимальный (90 кН/с), то при исследовании маневров (рис. 7–9) темп составлял 90/17,5 = 5,14 кН/с.
На рис. 7а отражено изменение сил и моментов при изменении значений горизонтального траста FTx (при базовых значениях hFTx, lFTz, fk0, сd, β). На рис. 7б приведены графики изменения ТСМ Mst при маневрировании квантомобиля для разных значений коэффициента сопротивления качению колес fk0 (при остальных – базовых).
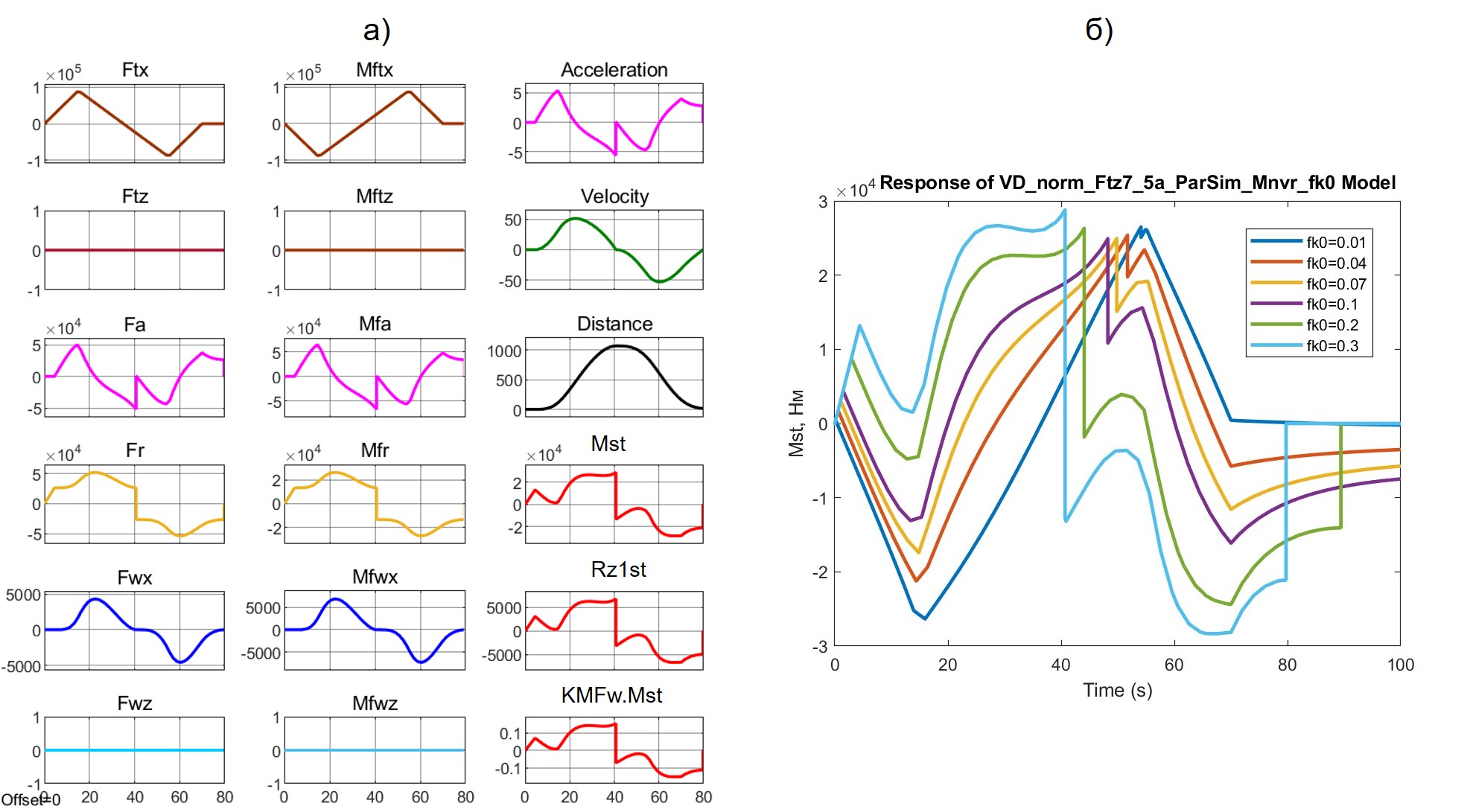
Рисунок 7 - Динамика сил и моментов при маневрировании:
а) распечатка продольного маневра на ОП с fk0 = 0,3; б) изменение Mst в серии маневров на ОП с различными fk0
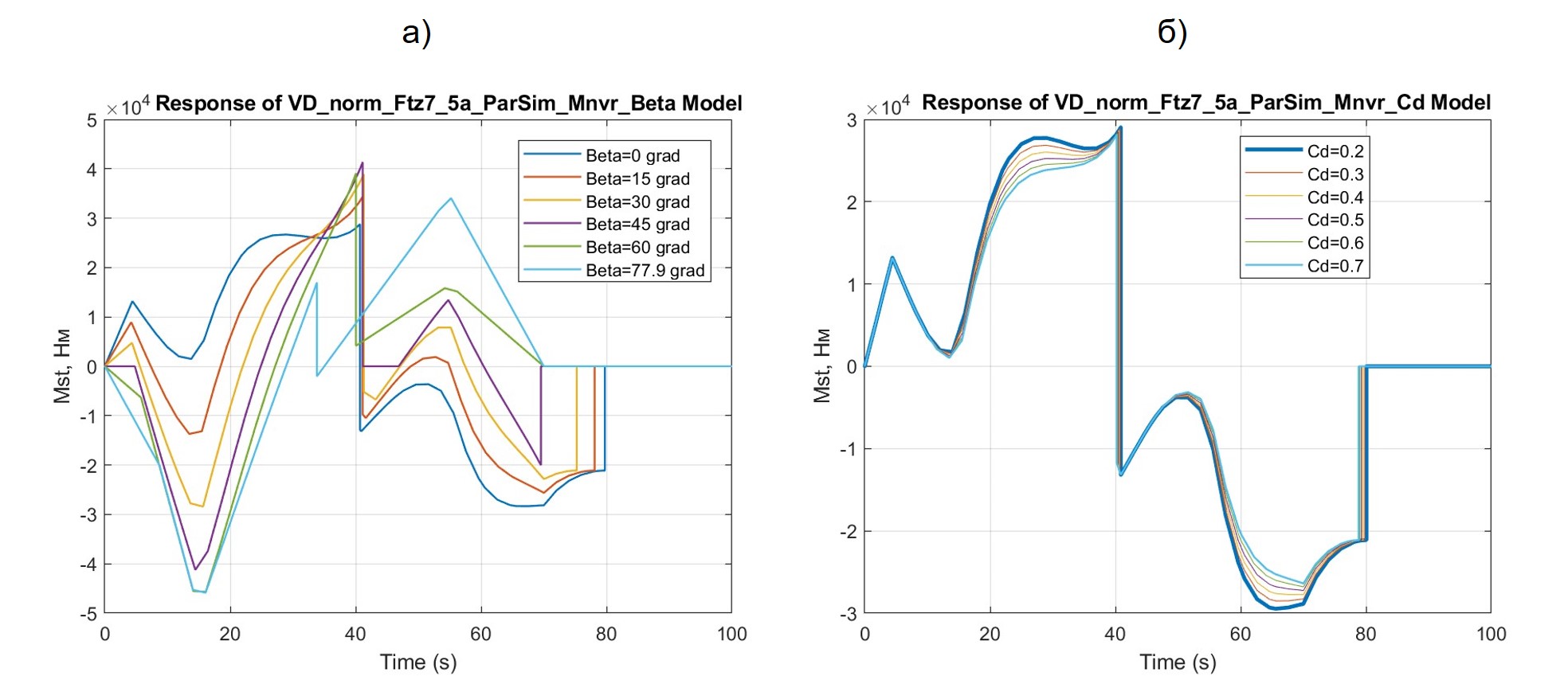
Рисунок 8 - Результаты расчетов процесса изменения ТСМ Mst при различных значениях угла β (а) и коэффициента драга cd (б)
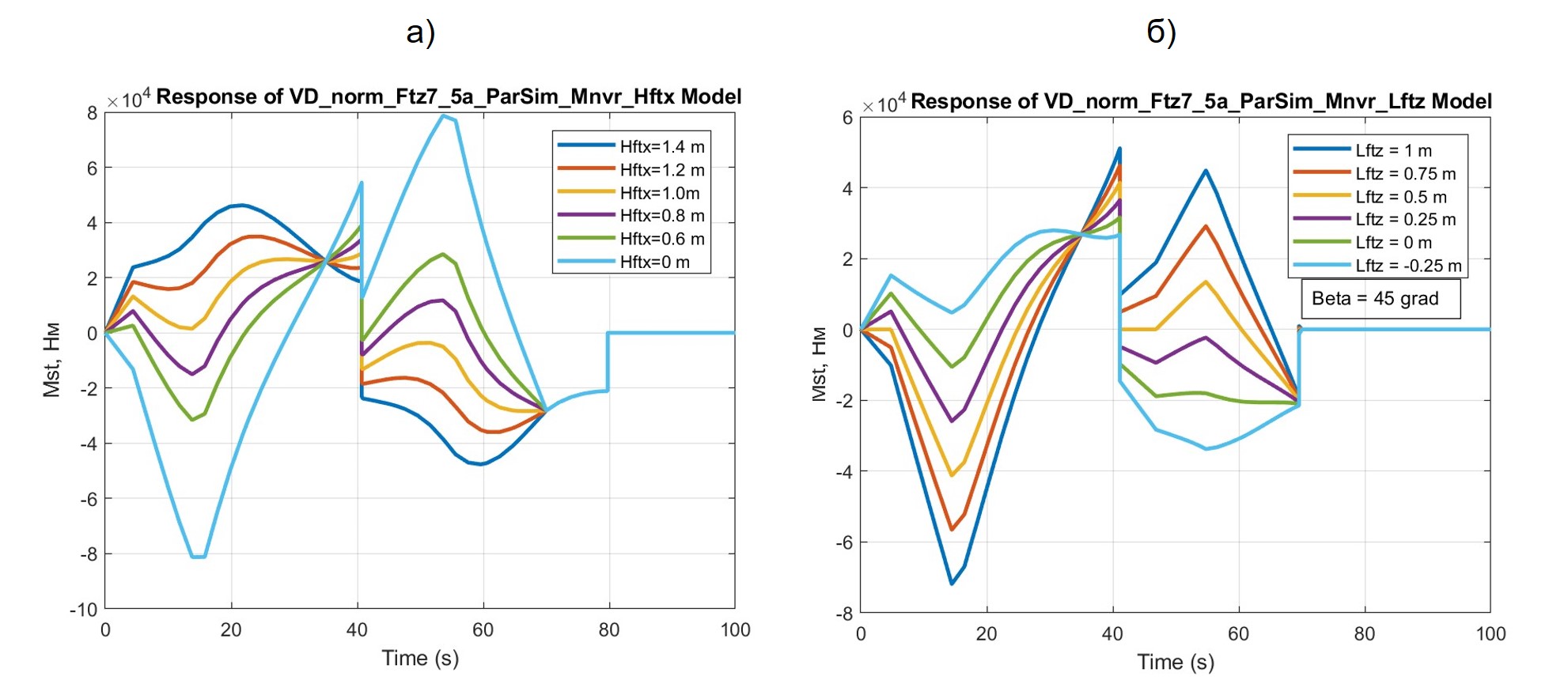
Рисунок 9 - Результаты расчетов процесса изменения ТСМ Mst при различных значениях hFTx (а) и lFTz (б)
4. Обсуждение
Обсудим несколько ситуаций. Естественно ожидать наибольшей потери устойчивости в крайних точках конструкционных особенностей, тяжелых условиях движения, резкой смены режимов движения.
Начнем с трогания колес и экипажа. Рассматриваем трогание в крайне тяжелых дорожных условиях (fk0 = 0,3). Было задано изменение траста FTx: первая секунда – рост до 90000 Н (см. FTx на рис. 4a).
Видим, что при β = 0 (FTz= 0) для Fr0 = fk0·(Gq–FTz) = 0,3·88000 = 26400 Н трогание колес происходит в момент времени t = 0,3 с – по достижении FTx = Fr = 26400 Н (см. также на рис. 4б кривую для β = 0). В промежутке 0 < t ≤ 0,3 c. Fr(t) = FTx(t), Fw(t) = 0, Fa(t) = 0 – и скорость, и ускорение равны нулю. Растущая сила FTx(t) целиком идет на накопление силы страгивания колес. Возникающий отрицательный динамический опрокидывающий момент запрашивает положительный реактивный момент со стороны ОП Mst(t) вплоть до 13000 Нм, соответственно реакция ОП на колеса передней оси Rz1st(t) растет до 3000 Н (экипаж «клюет»).
В интервале 0,3 c < t < 1 c FTx растет до максимума 90000 Н. Fr растет медленно. Растут ускорение и скорость – благодаря увеличивающейся разнице сил (FTx – Fr). Величины момента Mst(t) и силы Rz1st(t) падают (из-за больших ускорений экипажа, приводящих при росте момента MFa к подъему передка экипажа); при t = 0,8 с Mst(t) и Rz1st(t) переходят в отрицательную область.
При росте угла β вектора траста (см. рис. 4б) растет FTz, что приводит к снижению Fk0 (см. пики кривых на рис. 4б), а рост FTz(t) в пределах t <1c способствует снижению величины Fr. Эта особенность отражается и на характере кривых Mst = f (β) (см. рис. 5а).
Смена значений коэффициента fk0 приводит к пропорциональному изменению Fr0 и Fr(t), а также – к соответствующему характеру кривых Mst = f(fk0) (см. рис. 5б).
Направленность зависимости частного опрокидывающего момента (ОМ) от высоты действия горизонтального вектора траста hFTx очевидна – с уменьшением высоты и частный ОМ падает. Во взаимосвязи с другими составляющими общего ОМ создается ТСМ Mst, характер которого отражен на рис. 6а. Напомним, что уровень hFTx = 0 конструктивно нереален для квантомобиля, но, однако, соответствует схеме создания тяги традиционного автомобиля. Видим, что Mst квантомобиля существенно отличается от Mst автомобиля, и может приобретать даже другую направленность (см. hFTx > 1,2 м на рис. 6а).
Анализируя рис. 6а, отмечаем, что при hFTx > 1 м во всей фазе трогания наблюдается «клевок» экипажа (и Mst > 0), а при hFTx < 1 м передок напротив –приподнимается (и Mst < 0). При hFTx = 0 (напомним, это условный уровень действия траста, соответствующий уровню возникновения тяговой силы ведущих колес классического автомобиля) требуемый момент для устранения опрокидывания экипажа назад достигает величины Mst = –97000 Нм.
Направленность частного ОМ зависит от того, где находится точка пересечения линии действия наклонного вектора траста FT с ОП: спереди или сзади точки B на ОП (см. расположение точки CFT на рис. 3). Это объясняет топологическое расслоение семейства кривых Mst = f(lFTz) на рис. 6б на 2 группы: (в данном случае lFTz до 0,5 м и после).
Перейдем к маневрам. На рис. 7а видим трогание колес при значении Fr = FTx = 26400 Н. Отмечаем, что несмотря на достижение трастом нулевого значения на 35-ой секунде, выход скорости на нуль происходит на 40-й секунде – при этом наблюдается переброс Fr от 26400 Н до –26400 Н. Этим объясняется ступенчатое изменение ускорения, силы Fa, а также Mst и Rz1st. Экипаж, пройдя вперед 1050 м, вернулся к концу маневра на нулевую позицию.
Семейство кривых Mst = f(fk0,t) (рис.7б) отражает ожидаемую зависимость – с ростом fk0 растут и абсолютные значения ОМ. Рис. 7б также позволяет отметить отсутствие «зеркальности», как в характере (профиле), так и абсолютных значениях Mst на прямой и обратной ветвях маневра (объясняется отставанием динамики изменения скорости экипажа от динамики изменения задающего вектора FTx(t)).
Семейство кривых Mst = f(β,t) на рис. 8а свидетельствует, во-первых, о возможности большого разброса ОМ и МСТ в зависимости от угла β, а во-вторых, отсутствии «зеркальности» Mst на прямой и возвратной ветвях маневра.
Семейство кривых Mst = f(cd,t) на рис. 8б свидетельствует о том, что при существенной разнице привлеченных значений cd (от 0,2 до 0,7) разброс Mst наблюдался небольшим. Это объясняется тем, что в формирование Mst преобладающую долю вносит большое дорожное сопротивление (fk0 = 0,3), на фоне которых аэродинамические флюктуации малозначимы.
Особенности, проявившиеся на маневрах с изменением высоты действия траста hFTx:
1) с приближением к hFTx = 0 («автомобильный» вариант) передок экипажа (по ходу движения) все больше задирается (ТСМ Mst должен быть направлен на его сдерживание);
2) в момент перекладки направления траста FTx (рис. 9а) ТСМ Mst – ощутим (25000 Нм): из-за действующих в движении сопротивлений Fr и Fa;
3) в момент перекладки направления скорости (см. t = 40 с на рис. 7а) наблюдается резкая смена знака и величины Mst;
4) из-за инерционности и диссипативных потерь движущегося ТС «зеркальности» графиков на ветвях маневра не наблюдается.
Утверждение о влиянии точки пересечения линии действия наклонного траста FT с ОП (спереди или сзади точки B) на направленность частного ОМ остается в силе и для случая маневрирования. Однако заметим, что в силу непрерывности зависимости частного ОМ от lFTz поверхность Mst = f(lFTz,t) в пределах однонаправленной части маневра будет непрерывной (рис. 9а). При перекладке направления скорости движения, естественно, будет наблюдаться функциональный разрыв, как и во всех случаях с привлеченными здесь параметрами.
Совокупность проведенных расчетных экспериментов позволяет сделать следующие количественные выводы:
А. При троганиях и возвратно-поступательных маневрах квантомобиля можно ожидать значительных абсолютных ОМ MΣpm: для ТС с данными КамАЗ-4326 при троганиях в пределах –60 кНм < MΣpm <15 кНм; при маневрах –40кНм < MΣpm <40 кНм. С учетом того, что MΣpm /Lwb = Rz1, можно записать: для троганий –14 кН < Rz1 < 3,5 кН; а для маневров –9,5 кН < Rz1 < 9,5 кН. Если выразить эти неравенства в долях величины приложенного траста, т.е. Rz1/FT = ρz1, то получим (при FT = 90 кН): для троганий: –0,15 < ρz1 < 0,04; для маневров: –0,1 < ρz1 < 0,1.
Б. Для возвратно-поступательных маневров перепад значений MΣpm при перекладке направления траста и скорости движения достигает ∆MΣpm = 40 кНм, это соответствует броску ρz1 силовой нагрузки ∆Rz1 = 9,5 кН, что в долях к приложенному трасту составляет ∆ρz1 ≈ 0,1.
На значения величин Rz1, ∆Rz1, ρz1 и ∆ρz1 должны ориентироваться разработчики при установке стабилизирующих трастеров в зоне оси передних колес. При установке в других зонах ТС, естественно, нужно заменять Lwb другими величинами. Также естественно, что численные рекомендации будут иными при других конструктивных параметрах экипажа.
5. Заключение
Основными факторами, усугубляющими проблему устойчивости квантомобиля, в сравнении с классическим автомобилем, являются возникновение и реализация тяговой силы (траста) над опорной поверхностью (ОП), а также возможность вывешивания экипажа над ОП, что усиливает динамику движения в плоскости тангажа и увеличивает опасность опрокидывания. Многофакторные расчеты позволили оценить значимость этой проблемы.
Simulink-модель приземного движения квантомобиля (МПДК), созданная на базе рассмотрения схемы сил и моментов, действующих на ТС с квантовым двигателем (КД), привлечения математических моделей трогания и движения экипажа, позволила провести расчетное исследование динамики продольного движения квантомобиля при троганиях и продольных маневрах с фиксацией опрокидывающих моментов (ОМ) и требуемых стабилизирующих моментов (ТСМ) для нейтрализации ОМ.
Для нейтрализации опрокидывающих моментов на режимах трогания и маневрирования необходимы дополнительные трастеры, охватываемые единой системой управления с основным КД.
Сформированные на базе программы МПДК методические положения оценки продольной устойчивости квантомобиля могут послужить основой расчетной оптимизации компоновок этого вида ТС, расположения силовых модулей (трастеров) и их задействования в процессе движения.
Модель в целом может послужить как средством выработки конструктивных схем квантомобилей, так и оперативным решателем задействования дополнительных стабилизирующих трастеров на борту квантомобиля.
МПДК можно рассматривать как важную компоненту структуры дальнейших исследований функционирования квантомобиля средствами Matlab-Simulink и подобных пакетов прикладных программ.
