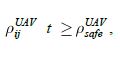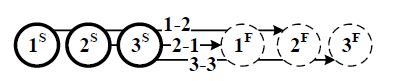SOLVING THE PROBLEM OF OPTIMAL REALIZABLE ASSIGNMENTS OF THE TARGET POSITIONS OF THE UAV AND DETERMINING THE ORDER OF MOVEMENT IN THE FORMATION PROBLEM WITH ENSURING TRAJECTORY SAFETY

Research article

Titkov I.P.

Karpunin A.A.

DOI:

https://doi.org/10.23670/IRJ.2022.118.4.016

Issue: № 4 (118), 2022

Published:

2022/04/18

PDF

DOI: https://doi.org/10.23670/IRJ.2022.118.4.016

РЕШЕНИЕ ЗАДАЧИ ОБ ОПТИМАЛЬНЫХ РЕАЛИЗУЕМЫХ НАЗНАЧЕНИЯХ ЦЕЛЕВЫХ ПОЛОЖЕНИЙ БПЛА И ОПРЕДЕЛЕНИИ ОЧЕРЕДНОСТИ ДВИЖЕНИЯ В ЗАДАЧЕ ФОРМАЦИИ С ОБЕСПЕЧЕНИЕМ ТРАЕКТОРНОЙ БЕЗОПАСНОСТИ

Научная статья

Титков И.П.¹, Карпунин А.А.^2,*

¹ORCID: 0000-0001-5023-7266;

²ORCID: 0000-0002-4117-5021;

^1,2 Московский государственный технический университет им. Н.Э. Баумана, Москва, Россия

^* Корреспондирующий автор (karpunin[at]bmstu.ru)

Аннотация

Рассматривается задача об оптимальных по критерию стоимости реализуемых назначениях целевых положений беспилотных летательных аппаратов (БПЛА) и определении очередности движения в задаче формации с обеспечением траекторной безопасности. Задача формации заключается в переводе БПЛА из начальной пространственной конфигурации в заданную конечную с поддержанием безопасного расстояния между БПЛА. Выявляется проблематика применения классической задачи о назначениях при перестроении строя с обеспечением траекторной безопасности. На модельном примере показывается наличие нескольких оптимальных назначений целевых положений БПЛА, часть которых оказывается нереализуемой. Ставится и решается задача об оптимальных реализуемых назначения целевых положений БПЛА в формации с определением очередности движения. Для этого классическая задача о назначениях дополняется ограничениями в виде условия реализуемости. Условие реализуемости требует существования очередности движения БПЛА из начальных положений в конечные, не допускающей нахождение переместившегося БПЛА на траектории еще не переместившегося. Предлагается алгоритм решения задачи об оптимальных реализуемых назначениях и алгоритм проверки реализуемости назначений и определения очередности движения. Приводятся примеры определения очередности движения и проверки реализуемости назначений. Исследуется производительность реализации предложенных алгоритмов и оценивается длительность вычислений.

Ключевые слова: беспилотный летательный аппарат, формация БПЛА, полет строем, задача о назначениях, траекторная безопасность.

SOLVING THE PROBLEM OF OPTIMAL REALIZABLE ASSIGNMENTS OF THE TARGET POSITIONS OF THE UAV AND DETERMINING THE ORDER OF MOVEMENT IN THE FORMATION PROBLEM WITH ENSURING TRAJECTORY SAFETY

Research article

Titkov I.P.¹, Karpunin A.A.^2,*

¹ ORCID: 0000-0001-5023-7266,

² ORCID: 0000-0002-4117-5021,

^1,2 Bauman Moscow State Technical University, Moscow, Russia

^* Corresponding author (karpunin[at]bmstu.ru)

Abstract

The current study examines the problem of optimal assignments of target positions of unmanned aerial vehicles (UAVs) according to the cost criterion and determining the order of movement in the formation problem with ensuring trajectory safety. The task of the formation is to transfer a UAV from the initial spatial configuration to a given final configuration with maintaining a safe distance between the UAVs. The study determines the problems of the application of the classical assignment problem in the reconstruction of the system with the provision of trajectory safety. The model example shows the presence of several optimal assignments of the target positions of the UAV, some of which turn out to be unrealizable. Also, the study poses and solves the problem of optimal realizable assignments of the target positions of the UAV in the formation with the determination of the sequence of movement. To do this, the classical assignment problem is supplemented by constraints in the form of a realizability condition. The feasibility condition requires the existence of a sequence of UAV movement from the initial positions to the final ones, which does not allow the UAV to be moved on the trajectory of the one that has not yet moved. The authors propose an algorithm for solving the problem of optimal implementable assignments and an algorithm for checking the feasibility of assignments and determining the order of movement; they also provide examples of determining the order of movement and checking the feasibility of assignments. The article investigates the performance of the implementation of the proposed algorithms and estimates the duration of calculations.

Keywords: unmanned aerial vehicle, UAV formation, formation flight, assignment task, trajectory safety.

Введение

В связи с ростом научно-прикладного интереса к тематике группового применения беспилотных летательных аппаратов (БПЛА) мультироторного типа увеличивается потребность в получении и использовании простых и эффективных способов планирования и управления движением группы БПЛА.

Среди задач управления группой БПЛА возможно выделить задачу построения заданного строя или формации (англ. formationtask) [1], [2]. В различных источниках задача построения и перестроения формации может называться по-разному, например, задача формирования строя группой БПЛА [3], [5], строевая задача [4].

Задача формации заключается в переводе БПЛА из начальной пространственной конфигурации в заданную конечную с поддержанием безопасного расстояния между БПЛА. Предполагается, что множество конечных положений в пространственной конфигурации известно, и их необходимо назначить конкретным БПЛА.

За последние годы опубликовано значительное количество работ, посвященных планированию и назначению траекторий движения групп БПЛА на основе различных подходов. Среди них можно выделить следующие.

Работа [13] основана на использовании теории графов: начальная и конечная формации описываются с помощью графов, переход из начального в конечное состояние осуществляется путем последовательных незначительных изменений весов ребер графа. После получения обновленного состояния графа решается задача о назначениях целевых положений для перевода группы в это состояние. Этот подход используется в [7] для перевода группы БПЛА из начальной формации в заданную. Предполагается, что за счет незначительных изменений текущего состояния формации, не произойдет столкновений и блокировок движения БПЛА.

В [18] выполняется синтез траекторий для отдельных БПЛА группы с последующим оптимальным назначением целевых положений на основе функции стоимости. Работы [16], [17], [19] отличаются используемыми критериями в целевой функции и подходами к планированию безопасных траекторий во времени.

В работе [3] для назначения БПЛА целевых положений в конечной формации используется метод итерационного улучшения плана, который не учитывает очередность движения БПЛА и требует выполнения итераций до достижения желаемого улучшения плана. В работах [6], [8] централизованный подход к выбору целевых положений в формации по критерию близости желаемых положений показывает более высокое быстродействие и лучшую сходимость по сравнению с децентрализованным подходом на основе роения. В работе [9] используется мультиагентный подход с составлением дискретного расписания движения для устранения коллизий. В [19] используется децентрализованный подход на основе аукциона. В [10] предлагается решение задачи определения самих желаемых положений в формации по заданному описанию этих положений. В [11] решается классическая задача о назначениях для двудольного графа, сформированного по расстояниям между начальными и конечными положениями на сфере.

В работе [14] сравниваются различные алгоритмы решения классической задачи о назначениях [12], [14], [15].

В большинстве из указанных работ важное место занимает приоритизация и планирование очередности движения для обеспечения траекторной безопасности. Несмотря на важность этих задач, они решаются на последних этапах при планировании траекторий движения во времени уже после решения задачи о назначениях. В настоящей работе показана необходимость выполнения приоритизации и первичного планирования очередности движения совместно с решением задачи о назначениях для предотвращения ситуаций, связанных с блокировками траекторий движения одними БПЛА других и приводящих к невозможности реализации формации.

Цель работы – получение способа назначения оптимальных реализуемых целевых положений БПЛА и определения очередности движения в задаче формации с обеспечением траекторной безопасности.

Данная работа может быть полезна для специалистов в различных областях при разработке не только систем управления группой БПЛА, способных к зависанию, но и мобильными робототехническими системами.

Постановка задачи

Задача об оптимальных реализуемых назначениях целевых положений БПЛА и определении очередности движения в задаче формации с обеспечением траекторной безопасности является комплексной. Для ее решения выполняется декомпозиция на отдельные задачи, которые ставятся и решаются в данной работе.

Постановка задачи формации группы БПЛА

Под состоянием группы БПЛА в данной работе понимается множество состояний БПЛА группы: положение и скорость центра масс (ЦМ) БПЛА, ориентация и угловая скорость БПЛА. Под формацией в данной работе понимается множество положений БПЛА группы.

Постановка задачи обеспечения траекторной безопасности группы БПЛА в задаче формации

В простейшем случае под траекторной безопасностью понимается отсутствие столкновений между БПЛА, БПЛА с препятствиями и положительная высота полета относительно подстилающей поверхности на всем интервале функционирования системы.

Отсутствие столкновений между БПЛА осуществляется за счет выполнения требований к безопасному расстоянию между БПЛА:

Проблематика классической задачи о назначениях в задаче формации с обеспечением траекторной безопасности

Фундаментальная задача о назначениях – задача о поиске минимальной суммы дуг во взвешенном двудольном графе, широко применяется для распределения заданий между БПЛА. При этом несмотря на эффективность ее применения возникают ситуации, в которых одного решения этой задачи недостаточно для назначения желаемых положений БПЛА.

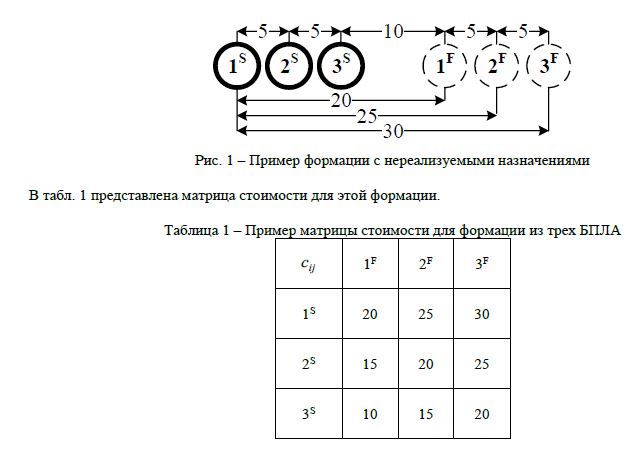
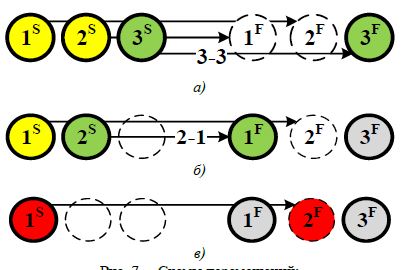
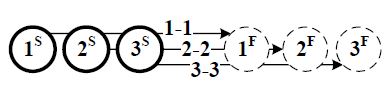
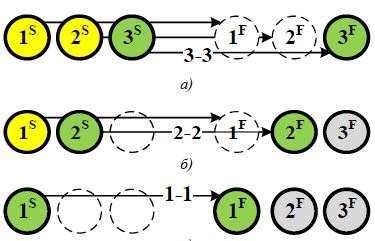
На рис. 1а представлен пример формации без пересечения траекторий движения БПЛА в целевые точки. На рис. 1б представлен пример формации с пересечением траекторий БПЛА. Для примеров, представленных на рис.1а и рис. 1б решение задачи о назначениях позволяет получить оптимальные назначения. На рис.1в представлен пример формации, для которой существует несколько оптимальных решений с одинаковой стоимостью, но при этом существуют назначения, не позволяющие остальным БПЛА достичь желаемых положений: если третий БПЛА займет первое положение в формации, то остальные окажутся заблокированными и не смогут достичь желаемых положений.

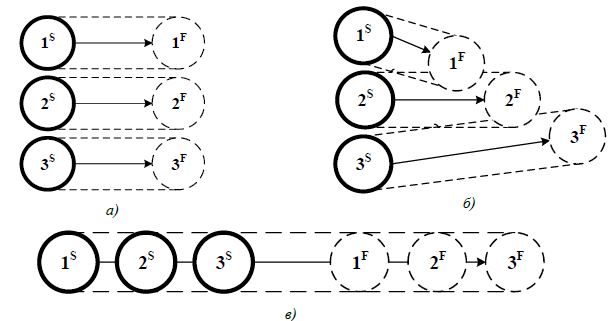Рис. 1 – Примеры формаций: а) без пересечения траекторий; б) с пересечением траекторий; в) с вложенными траекториями На рис. 1 показан пример формация для трех БПЛА со стоимостями перелета c11 20 , 12 c 25 , 13 c 30 , 21 c 15, 22 c 20, 23 c 25, 31 c 10, 32 c 15 , 33 c 20 из начальных положений S i в конечные положения F i , где i 1,2,3.

При решении классической задачи о назначениях существует несколько оптимальных решений с одинаковыми значениями функции стоимости: например, При этом единственное реализуемое назначение В остальных назначениях происходит блокировка одними БПЛА других.

Таким образом, использование для решения задачи формации только лишь классической задачи о назначениях является недостаточным по причине возможности получения оптимального решения в виде нереализуемых назначений. Возникает необходимость в получении оптимальных реализуемых назначений и определении очередности движении.

Постановка задачи об оптимальных реализуемых назначениях целевых положений БПЛА в формации с определением очередности движения

В широком смысле под формацией из точек понимается множество координат этих точек, а под формацией группы из N_UAV БПЛА – множество координат БПЛА. Целевая формация – множество координат, которые должны занять БПЛА группы.

В случае, если желаемые положения для каждого БПЛА в формации не назначены, то возникает необходимость в назначении каждому БПЛА такого положения.

В отличие от классической задачи о назначениях – поиске минимальной суммы дуг во взвешенном двудольном графе, в задаче об оптимальных реализуемых назначениях добавляется условие реализуемости назначений.

Условие реализуемости: должна существовать очередность движения БПЛА

Условие (3) имеет следующий смысл: -ый БПЛА с большим приоритетом перемещается из -го положения в начальной формации в ‑ое целевое положение в конечной формации раньше, чем БПЛА с меньшим приоритетом, и занимаемое им конечное положение не должно располагаться на траекториях -ых БПЛА с меньшим приоритетом .

Таким образом, формализованным решением задачи об оптимальных реализуемых назначениях целевых положений БПЛА и очередности движения в задаче формации будут назначенные БПЛА целевые положения и приоритеты такие, что суммарная стоимость перемещения в конечную формацию минимальная и назначение реализуемо.

Поставленная задача относится к классу задач нелинейного целочисленного программирования – в ее состав входят классическая задача о назначениях (задача линейного дискретного программирования) и задача определения очередности движения через целочисленные значения приоритетов и нелинейные условия реализуемости.

Решение задачи об оптимальных реализуемых назначениях целевых положений БПЛА в формации с определением очередности движения

Для решения задачи об оптимальных реализуемых назначениях целевых положений БПЛА в формации с определением очередности разработаны описанные ниже алгоритмы.

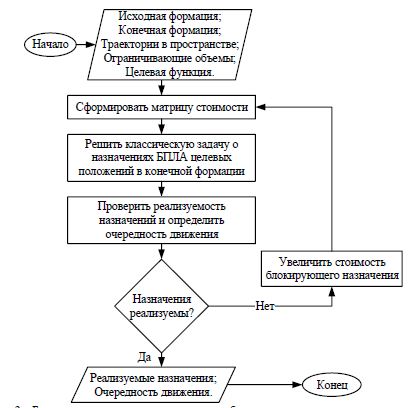
Алгоритм решения задачи об оптимальных реализуемых назначениях целевых положений БПЛА в формации с определением очередности движения

Входными данными алгоритма являются начальная и конечная формации, траектории в пространстве между точками начальной и конечной формаций, заданные ограничивающие объемы и их параметры (например, радиусы сфер) для проверки требований к безопасному расстоянию; целевая функция для решения классической задачи о назначениях. Выходными данными алгоритма являются оптимальные реализуемые назначения и очередность движения БПЛА.

По входным данным формируется исходная матрица стоимости. Для полученной матрицы стоимости решается классическая задача о назначениях любым известным способом. Проверяется реализуемость назначений. Если назначения нереализуемы, то стоимость блокирующего назначения (нахождение переместившегося БПЛА на траектории еще не переместившегося) принимается бесконечной и повторяются предыдущие шаги по решению классической задачи о назначениях для полученной матрицы стоимости до тех пор, пока не будут получены реализуемые назначения и очередность движения. На рис. 3 представлена блок-схема этого алгоритма.

Описание проверки реализуемости назначений с определением очередности движения представлено далее.

Рис. 3 – Блок-схема алгоритма решения задачи об оптимальных реализуемых назначениях и определении очередности движения

Предложенный алгоритм позволяет получить оптимальные реализуемые назначения БПЛА целевых положений в формации и определить безопасную очередность движения.

Алгоритм проверки реализуемости назначений и определения очередности движения

Для проверки реализуемости назначений и определения очередности движения разработан следующий алгоритм.

Входными данными являются текущие положения БПЛА, положения точек начальной и конечной формаций в пространстве и соединяющие их траектории и проверяемые назначения. Выходными данными являются реализуемость назначений и очередность движения, реализующая это назначение.

На подготовительном этапе формируются: три очереди – очередь хода, очередь ожидания, очередь движения (очередность движения); флаги переносов БПЛА из очереди движения в очередь хода (флаг «переноса» БПЛА). Очередь хода может быть заполнена произвольно индексами БПЛА группы или, например, в соответствии с назначениями, очередь ожидания – пустая, очередь движения – пустая.

Основной этап заключается в пошаговом выполнении действий:

если очередь хода не пустая, то необходимо выбрать первый БПЛА из очереди и принять решение о выполнении одного из четырех действий:
1. переместить выбранный БПЛА в конечное положение, соответствующее назначению, и перенести выбранный БПЛА из очереди хода в конец очереди движения, если на траектории движения отсутствуют конечные положения, занятые другими БПЛА;
2. перенести выбранный БПЛА из очереди хода в конец очереди ожидания, если на траектории движения выбранного БПЛА присутствует БПЛА, занимающий исходное положение;
3. оставить выбранный БПЛА в начале очереди хода, если на траектории движения выбранного БПЛА присутствует БПЛА, занявший конечное положение («блокирующий» БПЛА), и перенести «блокирующий» БПЛА из очереди движения в конец очереди хода, если флаг «переноса» «блокирующего» БПЛА не поднят;
4. завершить основной этап по причине блокировки траектории движения последним БПЛА из очереди движения, если на траектории движения выбранного БПЛА присутствует другой БПЛА, занявший целевое положение («блокирующий» БПЛА) и флаг «переноса» «блокирующего» БПЛА поднят.
если очередь ожидания не пустая, то БПЛА перемещаются из очереди ожидания в очередь хода и повторяются действия из предыдущего пункта; флаги «переносов» БПЛА сбрасываются.
если очередь ожидания и очередь хода пустые, то завершить основной этап по причине реализуемости назначений с полученной очередью движения (очередностью движения).

В результате выполнения описанных выше действий проверяется реализуемость назначений и определяется очередность движения БПЛА. Положение БПЛА в очереди движения соответствует его приоритету – БПЛА в начале очереди имеет больший приоритет и должен перемещаться раньше остальных.

Формализация условий принятия решений по перемещению (действие 1а), ожиданию (действие 1б) или выявления блокировки (действие 1г) для определения реализуемости и определения очередности движения представлена далее.

Формализация условий для определения очередности движения в задаче формации

Для определения очередности движения в задаче о реализуемых назначениях целевых положений БПЛА в конечной формации используются следующие три формальных условия:

Условия имеют следующий смысл: условие перемещения – БПЛА может переместиться, если на его траектории отсутствуют другие БПЛА; условие ожидания – БПЛА ожидает, если на его траектории находится БПЛА в начальном положении; БПЛА заблокирован, если на его траектории находится БПЛА в конечном положении. Проверки по этим условиям выполняются в статике, перемещение считается мгновенным.

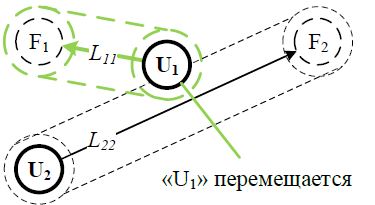
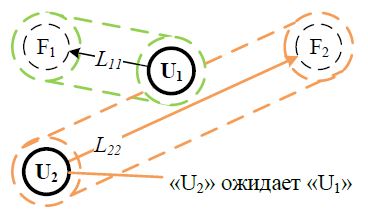
На рис. 4 показан пример выполнения условия перемещения – БПЛА «U₁» может переместиться из начального положения «S₁» в конечное положение «F₁», т.к. на его траектории отсутствуют другие БПЛА с большим приоритетом и его перемещение не заблокирует возможность перемещения БПЛА «U₂».

Рис. 4 – Иллюстрация условия перемещения БПЛА

На рис. 5 показан пример выполнения условия ожидания – БПЛА «U₂» ожидает перемещение БПЛА «U₁,» т.к. на его траектории находится БПЛА «U₁» с меньшим приоритетом в начальном положении «S₁»

Рис. 5 – Иллюстрация условия ожидания БПЛА

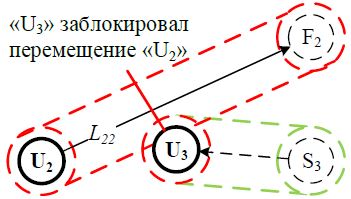
На рис. 6 показан пример выполнения условия блокировки – БПЛА «U₃» заблокировал перемещение БПЛА «U₂», т.к. занял конечное положение «F₃» на траектории еще не переместившегося БПЛА «U₂» с большим приоритетом.

Рис. 6 – Иллюстрация условия блокировки БПЛА

Описанные условия используются для проверки реализуемости назначений и определении очередности движения БПЛА.

Примеры проверки реализуемости назначений и определения очередности движения

Для пояснения работы описанных алгоритмов далее приводятся примеры проверки реализуемости назначений и определения очередности движения для формаций с нереализуемыми и реализуемыми назначениями.

Пример проверки нереализуемых назначений

На рис. 7 представлен пример нереализуемых назначений для формации из трех БПЛА с матрицей стоимости табл. 1. Очевидно, эти назначения нереализуемы причине блокировки вторым БПЛА, занявшим первое положение в формации, траектории движения первого БПЛА во второе положение в формации.

Рис. 7 – Пример нереализуемых назначений для формации из трех БПЛА

В табл. 2 приведена последовательность действий, выполненных для проверки реализуемости нереализуемых назначений (рис. 7).

Таблица 2 – Пример проверки нереализуемых назначений

№	Очередь хода	Очередь ожидания	Действие	Очередность движения
1	1, 2, 3	-	«U₁» ожидает «U₂»	-
2	2, 3	1	«U₂» ожидает «U₃»	-
3	3	1, 2	«U₃» занимает «3^F»	-
4	-	1, 2	Перенести очередь ожидания в очередь хода.	3
5	1, 2	-	«U₁» ожидает «U₂»	3
6	2	1	«U₂» занимает «1^F»	3
7	-	1	Перенести очередь ожидания в очередь хода и сбросить флаги «переноса»	3, 2
8	1, 2	-	Перенести «U₂» в конец очереди хода и поднять флаг «переноса» «U₂»	3
9	2	1	«U₁» ожидает «U₂»	3
11	1	-	Провал: перемещение «U₂» в «1^F» заблокировало путь «U₁» в «2^F» и флаг «переноса» «U₂» поднят.	3, 2

На рис. 8а‑8в представлена иллюстрация выполненных действий для проверки реализуемости назначений. На рис. 8а показано ожидание первым и вторым БПЛА перемещения третьего БПЛА и перемещение третьего БПЛА в третье целевое положение в формации. На рис. 8б показано перемещение второго БПЛА в первое целевое положение. На рис. 8в показана невозможность перемещения первого БПЛА во второе целевое положение по причине блокировки траектории движения БПЛА, занявшим второе целевое положение.

Рис. 8 – Схемы перемещений: а) «U₃» перемещается из «3^S» в «3^F», «U₁» и «U₂» ожидают перемещения «U₃»; б) «U₂» перемещается из «2^S» в «1^F»; «U₁» ожидает перемещение «U₂»; в) Перемещение «U₁» из «1^S» в «2^F» заблокировано «U₂», который занял конечное положение «1^F»

Из анализа результатов пошагового моделирования, представленных в табл. 2 и на рис. 8 следует, что назначения нереализуемы.

Пример проверки реализуемых назначений

На рис. 9 представлен пример реализуемых назначений для формации из трех БПЛА с матрицей стоимости табл. 1. Очевидно, эти назначения реализуемы – все аппараты двигаются друг за другом.

Рис. 9– Пример реализуемых назначений для формации из трех БПЛА

В табл. 3 приведена последовательность действий, выполненных для проверки реализуемости реализуемых назначений (рис. 9)

Таблица 3– Пример проверки реализуемых назначений

№	Очередь хода	Очередь ожидания	Действие	Очередность
1	1; 2; 3	-	«U₁» ожидает «U₂»	-
2	2; 3	1	«U₂» ожидает «U₃»	-
3	3	1; 2	«U₃» занимает «3^F»	-
4	-	1; 2	Перенести очередь ожидания в очередь хода	3
5	1; 2	-	«U₁» ожидает «U₂»	3
6	2	1	«U₂» занимает «2^F»	3,2
7	-	1	Перенести очередь ожидания в очередь хода
8	1	-	«U₁» занимает «1^F»	3; 2
9	-	-	Успех.	3; 2; 1

На рис. 10а-10в представлено пояснение выполненных действий для проверки реализуемости назначений. На рис. 10а показано ожидание первым и вторым БПЛА перемещения третьего БПЛА и перемещение третьего БПЛА в третье целевое положение в формации. На рис. 10б показано ожидание первым БПЛА второго и перемещение второго БПЛА во второе целевое положение. На рис. 10в показано перемещение первого БПЛА в первое целевое положение.

Рис. 10 – Схемы перемещений: а) «U₃» перемещается из «3^S» в «3^F», «U₁» и «U₂» ожидают перемещения «U₃»; б) «U₂» перемещается из «2^S» в «2^F»; «U₁» ожидает перемещение «U₂»; в) «U₁» перемещается из «1^S» в «1^F»

Из анализа результатов пошагового моделирования, представленных в табл. 3 и на рис. 10 следует, что назначения реализуемы.

Анализ решения задачи об оптимальных реализуемых назначениях желаемых положений БПЛА в конечной формации и определение очередности движения

Для решения задачи об оптимальных реализуемых назначениях последовательно решаются следующие частные задачи: планирование траекторий в пространстве между положениями в начальной и конечной формациях для формирования исходной матрицы стоимости и последующей проверки условия реализуемости (считаются известными); решение классической задачи о назначениях; проверка реализуемости назначений и определение очередности движения. Для анализа решения задачи проводятся вычислительные эксперимент по оценке длительности решения классической задачи о назначениях, вычислительные эксперименты по исследованию задачи об оптимальных реализуемых назначениях и определению очередности движения при отсутствии и при наличии нереализуемых назначений, оцениваются длительности решения.

Вычислительный эксперимент по оценке длительности решения классической задачи о назначениях

Для решения классической задачи о назначениях существует множество способов с различной вычислительной сложностью. Вычислительный эксперимент для оценки длительности решения классической задачи о назначениях проводится с применением венгерского алгоритма со сложностью . В табл. 4 представлены результаты: длительность решения одной классической задачи о назначениях и количество задач, которые возможно решить за одну секунду, в зависимости от количества положений в формации.

Таблица 4 – Длительность решения классической задачи о назначениях

Количество положений в формации	Длительность решения задачи, с	Количество решений за секунду
32	0,000152	6583
64	0,000191	5245
128	0,000829	1206
256	0,003922	254
512	0,025496	39
1024	0,164922	6
2048	1,165064	0
4096	7,849589	0

Экстраполирующая функция длительности решения классической задачи о назначениях для табл. 4 имеет вид .

Оценка длительности решения задачи об оптимальных реализуемых назначениях и определения очередности движения

Длительность проверки реализуемости назначений и определения очередности движения зависят от начальной очередности движения и класса траекторий, для которых проверяются условия.

Для проверки условий перемещения, ожидания и блокировки необходимо выполнить не более проверок принадлежности начальных и конечных точек формаций, траекториям, соединяющим все начальные точки формации со всеми конечными, где – количество точек в формации.

В простейшем случае для прямолинейных траекторий проверка этих условий сводится к вычислению не более расстояний между точкой и отрезком. В случае ломаных траекторий – не более вычислений, где – количество точек в формации, – общее количество звеньев ломаных.

Оценка длительности вычислений для случая прямолинейных траекторий может быть использована как оценка снизу, т.к. вычисление для остальных классов траекторий займет не меньше времени.

Определение очередности движения занимает не более трех проверок условий и перемещения между списками, каждый цикл проверок выполняется для уменьшающегося количества БПЛА от до 1. Наибольшее количество проверок может быть найдено как произведение количества типов проверок и суммы арифметической прогрессии количества БПЛА и составит не более проверок, где – количество БПЛА. Выполнение этих проверок возможно ускорить за счет распараллеливания. При проведении проверок ранее вычисленные значения расстояний возможно использовать повторно за счет кэширования.

Вычислительный эксперимент по исследованию задачи об оптимальных реализуемых назначениях и определению очередности движения при отсутствии нереализуемых назначений

Цель вычислительного эксперимента – оценка длительности решения задачи об оптимальных реализуемых назначениях и определению очередности движения при отсутствии нереализуемых назначений в зависимости от количества БПЛА в формации.

Исходные данные для вычислительного эксперимента – топология исходной и конечной формаций, количество БПЛА, требование к безопасному расстоянию. Топология исходной и конечной формаций представлены на рис. 11, формации расположены симметрично, расстояние между положениями в формациях одинаковое и больше безопасного, траектории – отрезки. В такой формации отсутствуют нереализуемые назначений.

Рис. 11 – Топология исходной и конечной формаций без нереализуемых назначений

Для заданной топологии исходной и конечной формаций варьируется количество БПЛА и решается задача о реализуемых назначениях и определяется очередность движения. В процессе решения определяются общее время решения задачи, время решения классической задачи о назначениях и время проверки реализуемости и определения очередности движения.

Методика оценки результатов вычислительного эксперимента:

1) оценивается процентная доля временных затрат на этапах решения;

2) экстраполируется зависимость общего времени решения в зависимости от количества БПЛА.

Оформление результатов проведения вычислительного эксперимента:

1) экстраполирующая функция и график зависимости общей длительности решения от количества БПЛА;

2) график зависимости временных затрат на этапах решения от количества БПЛА;

3) график зависимости долей временных затрат на этапах решения от количества БПЛА.

Результаты проведения вычислительного эксперимента

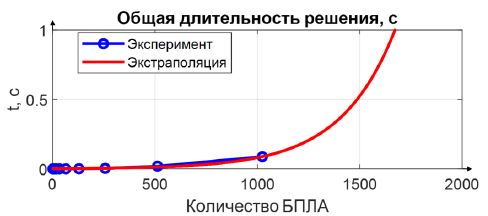
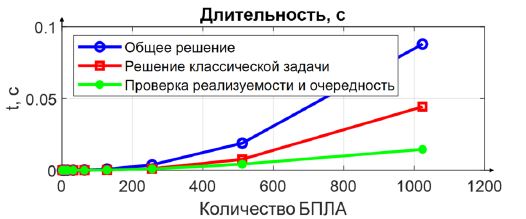
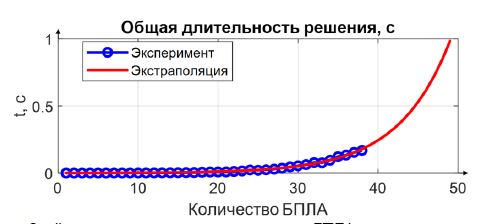
На рис. 12 показана зависимость общей длительности решения от количества БПЛА с экстраполирующей функцией .

Рис. 12 – Зависимость общей длительности решения от количества БПЛА без нереализуемых назначений

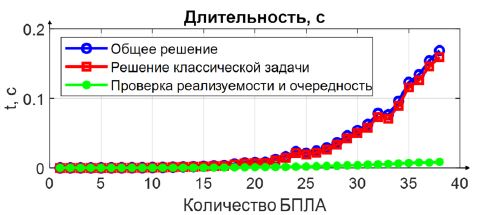
На рис. 13 показана зависимость длительности этапов решения общей задачи от количества БПЛА. Наибольшее количество времени уходит на решение классической задачи о назначениях, с увеличением количества БПЛА длительность ее решения растет быстрее, чем длительность проверки реализуемости назначений и определения очередности движения.

Рис. 13 – Зависимость длительности этапов решения общей задачи от количества БПЛА

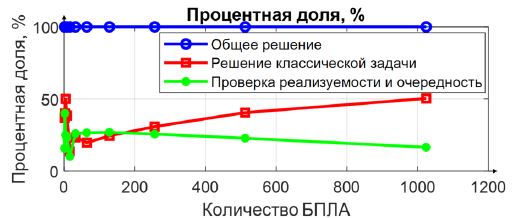
На рис. 14 показана зависимость процентных долей этапов решения общей задачи от количества БПЛА. С ростом количества БПЛА доля решения классической задачи о назначениях увеличивается.

Рис. 14 – Зависимость процентной доли этапов решения общей задачи от количества БПЛА

Из анализа представленных результатов следует, что при решении задачи об оптимальных реализуемых назначениях и определения очередности движения длительность проверки реализуемости и определения очередности не превосходит длительность решения классической задачи о назначениях.

Вычислительный эксперимент по исследованию задачи об оптимальных реализуемых назначениях и определению очередности движения при наличии нереализуемых назначений

Цель вычислительного эксперимента – оценка длительности решения задачи о нереализуемых назначениях и определению очередности движения при наличии нереализуемых назначениях и оценка количества нереализуемых назначений в зависимости от количества БПЛА в формации.

Исходные данные для вычислительного эксперимента – топология исходной и конечной формаций, количество БПЛА, требование к безопасному расстоянию. Топология исходной и конечной формаций представлены на рис. 15, формации расположены симметрично, расстояние между положениями в формациях одинаковое и больше безопасного, траектории – отрезки. Частный случай формации для трех БПЛА рассматривался выше – в такой формации присутствует несколько нереализуемых назначений.

Рис. 15 – Топология исходной и конечной формаций с нереализуемыми назначениями

Для заданной топологии исходной и конечной формаций варьируется количество БПЛА и решается задача о реализуемых назначениях и определяется очередность движения. В процессе решения считается количество нереализуемых назначений, определяются общее время решения задачи, время решения классической задачи о назначениях и время проверки реализуемости и определения очередности движения.

Методика оценки результатов вычислительного эксперимента

1) оценивается процентная доля временных затрат на этапах решения;

2) экстраполируется зависимость общего времени решения в зависимости от количества БПЛА.

Оформление результатов проведения вычислительного эксперимента:

1) экстраполирующая функция и график зависимости количества нереализуемых назначений от количества БПЛА;

2) экстраполирующая функция и график зависимости общей длительности решения от количества БПЛА;

3) график зависимости временных затрат на этапах решения от количества БПЛА; 4) график зависимости долей временных затрат на этапах решения от количества БПЛА.

Результаты проведения вычислительного эксперимента.

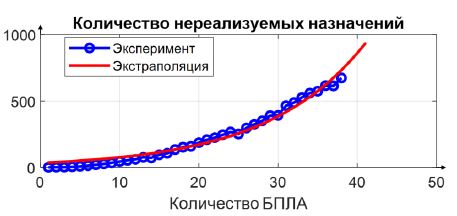
На рис. 16 показана зависимость количества нереализуемых назначений от количества БПЛА с экстраполирующей функцией . Зависимость нелинейная, количество нереализуемых назначений может в несколько раз превосходить количество БПЛА в формации.

Рис. 16 – Зависимость количества нереализуемых назначений от количества БПЛА

На рис. 17 показана зависимость общей длительности решения от количества БПЛА с экстраполирующей функцией .

Рис. 17 – Зависимость общей длительности решения от количества БПЛА при наличии нереализуемых назначений

На рис. 18 показана зависимость длительности этапов решения общей задачи от количества БПЛА. Наибольшее количество времени уходит на решение классической задачи о назначениях, проверка реализуемости и определение очередности движения с увеличением количества нереализуемых назначений имеет незначительную длительность.

Рис. 18 – Зависимость длительности этапов решения общей задачи от количества БПЛА при наличии нереализуемых назначений

На рис. 19 показана зависимость процентных долей этапов решения общей задачи от количества БПЛА. С ростом количества БПЛА увеличивается количество нереализуемых назначений и длительность решения общей задачи, при этом доля проверки реализуемости и определения очередности движения уменьшается.

Рис. 19 – Зависимость процентной доли этапов решения общей задачи от количества БПЛА

Из анализа представленных результатов следует, что длительность решения задачи об оптимальных реализуемых назначениях и определения очередности движения может оказаться узким местом при решении задачи формации при наличии множества нереализуемых назначений из-за повторяющегося решения классической задачи о назначениях. Для уменьшения влияния этого узкого места вместо повторного решения классической задачи о назначениях при выявлении нереализуемого назначения возможно выполнить его замену на назначение, не приводящее к изменению функции стоимости задачи.

Существенной особенностью, которую необходимо учитывать при решении задачи о назначениях целевых положений БПЛА в формации, является количество нереализуемых назначений, которое может в несколько раз превосходить количество БПЛА и нелинейно увеличивать длительность решения.

Управление группой БПЛА в задаче формации с обеспечением траекторной безопасности в виде последовательности перемещений

На основе полученного решения задачи о реализуемых назначениях целевых положений БПЛА и определении очередности движения в задаче формации с обеспечением траекторной безопасности возможно синтезировать простейший способ управления в виде последовательности перемещений. Суть способа сводится к последовательному перемещению каждого БПЛА из положения в начальной формации в назначенное целевое положение в конечной формации в соответствии с полученной очередностью движения – перемещение каждого последующего БПЛА начинается после завершения перемещения предыдущего с заданными требованиями к отклонению состояния БПЛА в целевом положении (например, заданные допустимые отклонения по скорости и по расстоянию от конечного положения). При применении этого способа общая длительность реализации формации складывается из длительностей перемещений каждого БПЛА по отдельности.

Заключение

В работе получены результаты исследования задачи об оптимальных реализуемых назначениях целевых положений БПЛА и определении очередности движения в задаче формации с обеспечением траекторной безопасности. Выявлена проблематика классической задачи о назначениях в задаче формации с обеспечением траекторной безопасности – оптимальные назначения, полученные в результате решения классической задачи, могут быть нереализуемыми. Для устранения выявленной проблемы сформированы условие реализуемости, предложена постановка и решена задача об оптимальных реализуемых назначениях целевых положения БПЛА в формации с определением очередности движения. Предложен алгоритм проверки реализуемости назначений и определения очередности движения. Выявлена необходимость учета возможного наличия нереализуемых назначений, количество которых может в несколько раз превосходить количество БПЛА в формации и нелинейно увеличивать длительность решения задачи. Предложен простейший способ управление группой БПЛА в задаче формации с обеспечением траекторной безопасности в виде последовательности перемещений на основе полученной очередности движения. Полученные результаты вычислительных экспериментов подтверждают необходимость в проверке реализуемости назначений и эффективность предложенного решения задачи об оптимальных реализуемых назначениях – в модельном примере с нереализуемыми назначениями и прямолинейными траекториями для группы с численностью до 32 БПЛА решение возможно получить менее чем за одну секунду, при отсутствии нереализуемых столкновений – до 1024 БПЛА.

Конфликт интересов	Conflict of Interest
Не указан.	None declared.

Список литературы / References

1. Видов К.С. Программно-алгоритмическое обеспечение режима группового самолетовождения. /К.С.Видов, Д.И. Гусев // Электронный журнал «Труды МАИ». – 2011. – № – 14 с.
2. Гусев Д.И. Решение задачи автоматизации полета группы самолетов. / Д. И. Гусев. // Электронный журнал «Труды МАИ». –2012. – №51. – 21 с.
3. Дьяченко А.А. Задача формирования строя в группе БПЛА / А.А. Дьяченко // Известия Южного федерального университета. Технические науки. – 2012. – Т. 128, № 3. – С.22‑30.
4. Иванов Д.Я. Решение строевой задачи в группе беспилотных квадрокоптеров / Д.Я. Иванов // Известия Южного федерального университета. Технические науки. – 2014. – Т. 157, № 8. – С. 138-147.
5. Иванов Д.Я. Формирование строя группой беспилотных летательных аппаратов при решении задач мониторинга / Д.Я. Иванов // Известия ЮФУ. Техническиенауки. – 2012. – Т. 129, № 4. – С. 219-224.
6. Image and animation display with multiple mobile robots./ J.Alonso-Mora, A.Breitenmoser, M. Rufli et al. // The International Journal of Robotics Research. – 2012. – Vol. 31(6). –pp. 753–773. DOI:10.1177/0278364912442095.
7. Fernando M.Formation Control and Navigation of a Quadrotor Swarm. / M.Fernando, L. Liu // 2019 International Conference on Unmanned Aircraft Systems (ICUAS). – 2019.– P. 284–291, DOI:10.1109/ICUAS.2019.8798352.
8. Multi-Robot Formation Control via a Real-Time Drawing Interface. Field and Service Robotics / S.Hauri, J.Alonso-Mora, A.Breitenmoser et al.// Springer Tracts in Advanced Robotics. –2014. – Vol. 92. – P. 175– DOI: 10.1007/978-3-642-40686-7_12.
9. Trajectory Planning for Quadrotor Swarms / W.Hoenig, Aр.J. Preiss, T. K. S.Kumar et al.// IEEE Transactions on Robotics. –2018. – Vol. 34, No. 4.– P. 856– DOI: 10.1109/TRO.2018.2853613.
10. Ivanov D.Formation Task in a Group of Quadrotors. / Ivanov D., Kalyaev I., Kapustyan S. // Advances in Intelligent Systems and Computing.– 2015. – Vol. 345.– pp. 183–191. DOI:10.1007/978-3-319-16841-8_18.
11. Khachumov M.The model of UAV formation based on the uniform allocation of points on the sphere /M.Khachumov, V. Khachumov // MATEC Web Conf. – Vol. 161, Art.ID: 03022, 2018. – P. 1-4. DOI:10.1051/matecconf/201816103022.
12. Kuhn H.W. The hungarian method for the assignment problem / H.W. Kuhn // Naval Research Logistics Quarterly. – 1955. – Vol. 2 (1-2). – P. 83–97.
13. Liu L. Multi-Robot Formation Morphing through a Graph Matching Problem / L.Liu, D.A. Shell // Springer Tracts in Advanced Robotics.– 2014. – Vol 104. – P. 291–306. DOI:1007/978-3-642-55146-8_21.
14. Dell'AmicoM.Algorithms and codes for dense assignment problems: the state of the art / . M. Dell'Amico, P. Toth. // Discrete Applied Mathematics. – 2000.– Vol. 100, No. 1–2. – P. 17– DOI: 10.1016/S0166-218X(99)00172-9.
15. Munkres J. Algorithms for the assignment and transportation problems / J. Munkres// Journal of Society for Industrial and Applied Mathematics. –1957. – Vol. 5(1).– P. 32–38.
16. Turpin M. Capt: Concurrent assignment and planning of trajectories for multiple robots / M.Turpin, N.Michael, Kumar // The International Journal of Robotics Research. 2014. – Vol. 33. – P. 98–112.
17. Turpin M. Trajectory Planning and Assignment in Multirobot Systems/ M.Turpin, N.Michael, V. Kumar // Springer Tracts in Advanced Robotics. –2013. – Vol. 86. – pp. 175-190. DOI:10.1007/978-3-642-36279-8_11.
18. Goal assignment and trajectory planning for large teams of interchangeable robots / M.Turpin, N.Michael, V. Kumar et al. // Autonomous Robots. – 2014. – Vol. 37(4). – P. 401–415. DOI:10.1007/s10514-014-9412-1.
19. Collision-aware Task Assignment for Multi-Robot Systems. / F. Wu et al. // International Symposium on Multi-Robot and Multi-Agent Systems (MRS) (2019). – 2019. – P. 30–36. DOI:10.1109/MRS.2019.8901059.

Список литературы на английском языке / References in English

Vidov K.S. Programmno-algoritmicheskoe obespechenie rezhima gruppovogo samoletovozhdenija [Software-algorithmic support of the group piloting mode] / K.S.Vidov, D.I. Gusev // Jelektronnyj zhurnal «Trudy MAI». 2011, № 14 p. [in Russian]
Gusev D.I. Reshenie zadachi avtomatizacii poleta gruppy samoletov [Solving the problem of automating the flight of a group of aircraft] / D.I. Gusev // Jelektronnyj zhurnal «Trudy MAI». № 51, 2012. 21 p. [in Russian]
D'jachenko A.A. Zadacha formirovanija stroja v gruppe BPLA [The task of forming structure in group of UAVs] / A. D'jachenko // Izvestija Juzhnogo federal'nogo universiteta. Tehnicheskie nauki. 2012. V. 128, № 3. P. 22–30. [in Russian]
Ivanov D.Ja. Reshenie stroevoj zadachi v gruppe bespilotnyh kvadrokopterov [Solving of a formation task in a group of unmanned quadrotors] /D.Ja. Ivanov // Izvestija Juzhnogo federal'nogo universiteta. Tehnicheskie nauki. 2014. V. 157, № 8. P. 138–147. [in Russian]
Ivanov D.Ja. Formirovanie stroja gruppoj bespilotnyh letatel'nyh apparatov pri reshenii zadach monitoring [Formation of structure by group of unmanned aerial vehicles in tasks of monitoring] // Izvestija JuFU. Tehnicheskie nauki. 2012. V. 129, № 4. P. 219-224. [in Russian]
Image and animation display with multiple mobile robots./ J.Alonso-Mora, A.Breitenmoser, M. Rufli et al. // The International Journal of Robotics Research. – 2012. – Vol. 31(6). –pp. 753–773. DOI:10.1177/0278364912442095.
Fernando M.Formation Control and Navigation of a Quadrotor Swarm. / M.Fernando, L. Liu // 2019 International Conference on Unmanned Aircraft Systems (ICUAS). – 2019.– P. 284–291, DOI:10.1109/ICUAS.2019.8798352.
Multi-Robot Formation Control via a Real-Time Drawing Interface. Field and Service Robotics / S.Hauri, J.Alonso-Mora, A.Breitenmoser et al. // Springer Tracts in Advanced Robotics. – 2014. – Vol. 92. – P. 175– DOI: 10.1007/978-3-642-40686-7_12.
Trajectory Planning for Quadrotor Swarms / W.Hoenig, Aр.J. Preiss, T. K. S.Kumar et al. // IEEE Transactions on Robotics. – 2018. – Vol. 34, No. 4.– P. 856– DOI: 10.1109/TRO.2018.2853613.
Ivanov D.Formation Task in a Group of Quadrotors. / Ivanov D., Kalyaev I., Kapustyan S. // Advances in Intelligent Systems and Computing.– 2015. – Vol. 345.– pp. 183–191. DOI:10.1007/978-3-319-16841-8_18.
Khachumov M.The model of UAV formation based on the uniform allocation of points on the sphere /M.Khachumov, V. Khachumov // MATEC Web Conf. – Vol. 161, Art.ID: 03022, 2018. – P. 1-4. DOI:10.1051/matecconf/201816103022.
Kuhn H.W. The hungarian method for the assignment problem / H.W. Kuhn // Naval Research Logistics Quarterly. – 1955. – Vol. 2 (1-2). – P. 83–97.
Liu L. Multi-Robot Formation Morphing through a Graph Matching Problem / L.Liu, D.A. Shell // Springer Tracts in Advanced Robotics.– 2014. – Vol 104. – P. 291–306. DOI:1007/978-3-642-55146-8_21.
Dell'AmicoM. Algorithms and codes for dense assignment problems: the state of the art / . M. Dell'Amico, P. Toth. // Discrete Applied Mathematics. – 2000.– Vol. 100, No. 1–2. – P. 17– DOI: 10.1016/S0166-218X(99)00172-9.
Munkres J. Algorithms for the assignment and transportation problems / J. Munkres// Journal of Society for Industrial and Applied Mathematics. –1957. – Vol. 5(1).– P. 32–38.
Turpin M. Capt: Concurrent assignment and planning of trajectories for multiple robots / M.Turpin, N.Michael, Kumar // The International Journal of Robotics Research. 2014. – Vol. 33. – P. 98–112.
Turpin M. Trajectory Planning and Assignment in Multirobot Systems/ M.Turpin, N.Michael, V. Kumar // Springer Tracts in Advanced Robotics. –2013. – Vol. 86. – pp. 175-190. DOI:10.1007/978-3-642-36279-8_11.
Goal assignment and trajectory planning for large teams of interchangeable robots / M.Turpin, N.Michael, V. Kumar et al. // Autonomous Robots. – 2014. – Vol. 37(4). – P. 401–415. DOI:10.1007/s10514-014-9412-1.
Collision-aware Task Assignment for Multi-Robot Systems. / F. Wu et al. // International Symposium on Multi-Robot and Multi-Agent Systems (MRS) (2019). – 2019. – P. 30–36. DOI:10.1109/MRS.2019.8901059.