CALCULATION OF CO 2 TRANSFER IN THE ATMOSPHERE BASED ON THE GENERAL ATMOSPHERIC CIRCULATION MODEL

НАУКИ О ЗЕМЛЕ / SCIENCE ABOUT THE EARTH

DOI: https://doi.org/10.23670/IRJ.2022.118.4.072

РАСЧЕТ ПЕРЕНОСА CO₂ В АТМОСФЕРЕ НА БАЗЕ МОДЕЛИ ОБЩЕЙ ЦИРКУЛЯЦИИ АТМОСФЕРЫ

Научная статья

Пархоменко В.П.^*

ORCID: 0000-0002-9963-0496,

Федеральный исследовательский центр «Информатика и управление» Российской Академии, Москва, Россия

^* Корреспондирующий автор (vparhom[at]yandex.ru)

Аннотация

Целью данной работы является изучение подходов к построению совместной модели, включающей взаимодействующие глобальные модель климата и модель цикла углерода, описывающую продукционный процесс в масштабе планеты. Основной задачей этого этапа исследования была отработка методики расчета переноса и вертикального перемешивания CO₂ в атмосфере на базе модели общей циркуляции атмосферы и оценка влияния этих процессов на его концентрацию в атмосфере. Для описания продукционных процессов применена модель с 7 типами растительности и упрощенным описанием фотосинтеза. Приведены результаты численных экспериментов с применением этого комплекса моделей.

Ключевые слова: цикл СО₂, модель общей циркуляции атмосферы, численные эксперименты.

CALCULATION OF CO ₂ TRANSFER IN THE ATMOSPHERE BASED ON THE GENERAL ATMOSPHERIC CIRCULATION MODEL

Research article

Parkhomenko V.P.^*

ORCID: 0000-0002-9963-0496,

Federal Research Center «Informatics and Management» of the Russian Academy of Sciences, Moscow, Russia

^* Corresponding author (vparhom[at]yandex.ru)

Abstract

The current article aims to examine approaches to the construction of a joint model that includes an interacting global climate model and a carbon cycle model that describes the production process on a global scale. The main task of this stage of the study was to develop a methodology for calculating the transport and vertical mixing of CO ₂ in the atmosphere based on a model of the general circulation of the atmosphere and to assess the impact of these processes on its concentration in the atmosphere. To describe the production processes, the study uses a model with 7 types of vegetation and a simplified description of photosynthesis. The article also presents the results of numerical experiments using this set of models.

Keywords: CO ₂ cycle, general atmospheric circulation model, numerical experiments.

Введение

Особое место при анализе биогеохимических циклов имеет круговорот (цикл) углерода. Сухое органическое вещество примерно наполовину состоит из углерода. Углерод в атмосфере находится в основном в виде парникового газа - двуокиси углерода, а значит, влияет на климат планеты [1].

Продуктом фотосинтеза является органическое вещество растений и кислород, который поступает в атмосферу и затем используется в процессе дыхания всеми живыми организмами, в том числе и самими растениями.

Практически вся биомасса сосредоточена на суше - суммарное количество углерода в живом органическом веществе суши примерно такое же, как и количество углерода в атмосфере (соответственно, 1000 млрд. т и 700 млрд. т.) Количество углерода в живом веществе океана почти в 15 тыс. раз меньше, чем углерода в растительности на суше.

Закономерности распределения растительности на суше определяются в основном климатическими факторами - наличием тепла и влаги. Максимальное значение массы растительности на единицу площади наблюдается в тропическом поясе (наиболее обеспеченном теплом) в лесах. Недостаток влаги в этом же поясе сопровождается резким обеднением жизни в тропических пустынях. Недостаток тепла в высоких широтах определяет малую биомассу растительности в Арктике.

Целью данной работы является изучение подходов к построению совместной модели, включающей взаимодействующие глобальные модель климата и модель цикла углерода, описывающую продукционный процесс в масштабе планеты. Антропогенные выбросы могут быть эффективно учтены сценарным образом. Отработана методика расчета переноса и вертикального перемешивания CO₂ в атмосфере на базе модели общей циркуляции атмосферы. Проведена оценка влияния этих процессов на концентрацию этого газа в атмосфере. В настоящее время представляется актуальным и практически значимым, в частности, для прогнозирования климатических изменений, разработка комплекса глобальных моделей, описывающих совместное функционирование климата и биосферы. Частью этого исследования является настоящая работа.

Описание комплекса моделей и основные результаты

Для описания глобальных продукционных процессов применена упрощенная модель с 7 типами растительности (тундра, лес, полупустыня, степи, мелколесье, пустыня, континентальный лед) и упрощенным описанием фотосинтеза.

Цикл углерода для каждого типа поверхности описывается дифференциальным уравнением [2], [3], [4]:

где P_min - минимальные осадки, при которых начинается фотосинтез (фиксируется своё значение для каждого из 7 экотипов).

Функция f(I) определяет зависимость фотосинтеза от типа поверхности I.

В простейшем случае дыхание поддержания можно считать пропорциональным фотосинтезу. Член  имеет сложный вид зависимости от осадков, температуры и количества гумуса в ячейке. В данном случае  не учитываем, т.к. не влияет на характерный вид кривой годичной продукции.

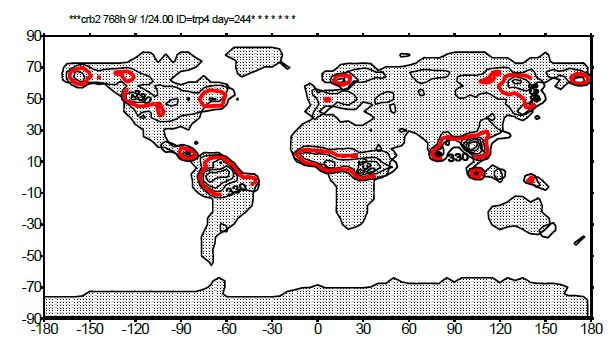
Начальное распределение CO₂ в атмосфере предполагается равномерным с концентрацией 360 ppm. На рисунке 1 показано установившееся распределение концентрации CO₂ на нижнем расчетном уровне для августа месяца при отсутствии пространственного переноса углекислого газа. Области пониженной концентрации (330 ppm и менее) выделены жирными изолиниями и определяют области интенсивного. На верхнем расчетном уровне, как и следовало ожидать, концентрация остается неизменной.

Рис. 1 – Распределение концентрации CO₂ на нижнем расчетном уровне для августа месяца при отсутствии пространственного переноса

Из полученных результатов следует, что модель качественно верно воспроизводит относительную величину сезонных колебаний, а также распределение CO₂ в атмосфере. Кроме того, воспроизводится общая тенденция к снижению амплитуды сезонных колебаний продукции в атмосфере по мере приближения к экватору.

Модель общей циркуляции атмосферы [5], [6], описывает тропосферу, расположенную ниже предполагаемого уровня изобарической тропопаузы (200 мбар). Система трехмерных дифференциальных уравнений модели атмосферы, так называемая система примитивных уравнений [6], [7], включает в себя уравнение, описывающее гидростатическое приближение по вертикали, прогностическое уравнение, описывающее закон сохранения массы сухого воздуха, прогностическое уравнение для сохранения влагосодержания в атмосфере, динамические прогностические уравнения для горизонтальных компонент скорости и термодинамическое уравнение сохранения энергии. Уравнения дополняются соответствующими граничными условиями и, таким образом, получается замкнутая динамическая система.

Для определения источников водяного пара и тепла применяются модели, описывающие гидрологический цикл и процессы распространения теплового и солнечного излучения [8]. Испарение, конденсация и конвекция зависят от термического состояния атмосферы, которое в свою очередь является функцией обмена теплом, имеющим место в этих процессах. На каждом шаге модифицируется термическое состояние атмосферы, новые значения температуры используются на следующем шаге.

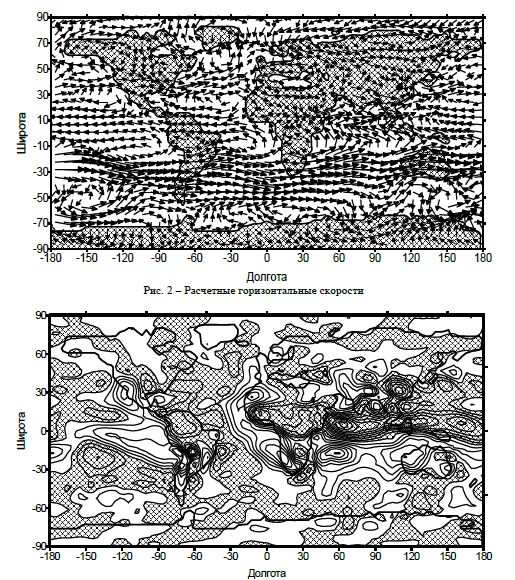
Рис. 3 – Изолинии поля вертикальной скорости

На рисунке 2 показаны результаты расчетов поля горизонтальных скоростей воздуха на уровне 800 Мбар, позволяющие использовать их для расчета дальнего переноса атмосферного CO₂. На рисунке 3 приведены изолинии вертикальных потоков воздуха. Заштрихованные области определяют направленный вверх перенос, остальные – направленный вниз. Их анализ позволяет судить о поведении примесей в атмосфере.

Рассчитанные и осредненные за сутки скорость ветра, приземная температура, осадки, нагревание поверхности в каждой расчетной ячейке используются в модели биогеохимического цикла. В свою очередь, характеристики растительного покрова и концентрация CO₂ определяются в модели биогеохимического цикла и оказывают влияние на климатические характеристики через парниковый эффект

Для описания процессов переноса CO₂ в атмосфере используется уравнение переноса примеси в атмосфере [5], [9]. Оно имеет следующий вид:

где π – определяется давлением воздуха, σ – вертикальная координата, t – время, c – концентрация CO₂ в атмосфере,  - источники или стоки CO₂ на подстилающей поверхности, определяющиеся продукционными процессами. Скорости V в данном уравнении определяются в модели атмосферы. Концентрация вычисляется на двух основных расчетных уровнях по вертикали.

Уравнение переноса решается с шагом по времени, совпадающим с шагом решения уравнений циркуляции атмосферы [10]. Правая часть уравнения вычисляется один раз в сутки из модели продукционного процесса.

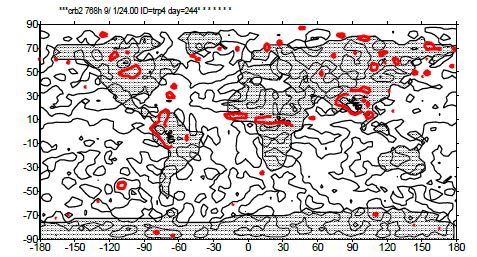
На рисунке 4 показаны результаты расчета распределения концентрации CO₂ с учетом переноса для нижнего расчетного уровня. Области пониженной концентрации существенно уменьшились и несколько сместились в результате переноса и перемешивания на нижнем уровне. На верхнем уровне развивается слабая неравномерность распределения, что связано с отсутствием источников CO₂ в атмосфере и наличием вертикальных потоков.

Рис. 4 – Распределение концентрации CO₂ на нижнем расчетном уровне с учетом переноса для августа месяца

Заключение

Учет в модели суточного и сезонного переноса СО₂ в атмосфере позволил описать динамику изменения концентрации СО₂ для всей атмосферы. Отработана методика расчета переноса и вертикального перемешивания CO₂ в атмосфере на базе модели общей циркуляции атмосферы. Проведена оценка влияния этих процессов на концентрацию этого газа в атмосфере. Учет этих процессов приводит к сглаживанию горизонтальных неоднородностей распределения СО₂.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. IPCC, 2014: Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Core Writing Team, R.K. Pachauri and L.A. Meyer (eds.)]. IPCC, Geneva, Switzerland, 151 p.
2. Тарко А.М. Математические модели глобальных и региональных процессов в биосфере / А.М. Тарко // Общая и прикладная ценология. № 6, 2007, С. 44-47.
3. Тарко А.М. Антропогенные изменения глобальных биосферных процессов. Математическое моделирование: монография / А.М. Тарко. - М.: Физматлит, 2005. - 232 с.
4. Пархоменко В.П. Глобальная климатическая модель с учетом биогеохимического углеродного цикла растительности суши / В.П. Пархоменко // Математическое моделирование и численные методы, 2021, № 2, с. 38–53.
5. Пархоменко В.П. Организация численных экспериментов на модели общей циркуляции атмосферы и глобальной модели океана / В.П. Пархоменко // Журнал вычислительной математики и математической физики 2021, Vol. 61, No. 10, pp. 1693–1703.
6. Толстых М.А. Модели глобальной атмосферы и мирового океана: алгоритмы и суперкомпьютерные технологии / М.А. Толстых, Р.А. Ибраев и др. М: Изд-во МГУ, 2013. 144 с.
7. Педлоски Дж. Геофизическая гидродинамика, том1 / Дж. Педлоски. - М.: Мир, 1984. - 398 с.
8. Пархоменко В. П. Применение глобальных климатических моделей для исследования климата Земли / В.П. Пархоменко // Труды Института системного анализа Российской академии наук (Труды ИСА РАН). – 2018. – Т. 68, №2. – C. 38–41.
9. Parkhomenko V.P. Modeling of global and regional climate response to solar radiation management / V.P. Parkhomenko // IOP Journal of Physics: Conference Series. – 2018 – V.1141, 012057. – P. 1-5. DOI:10.1088/1742-6596/1141/1/012057
10. Shepherd J. G. Overcoming the CFL time-step limitation: a stable iterative implicit numerical scheme for slowly evolving advection-diffusion systems / J. G. Shepherd // Ocean Modelling. 2002. V.4. P. 17-28.

Список литературы на английском языке / References in English

1. IPCC, 2014: Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Core Writing Team, R.K. Pachauri and L.A. Meyer (eds.)]. IPCC, Geneva, Switzerland, 151 p.
2. Tarko A.M. Matematicheskie modeli global'nyh i regional'nyh processov v biosfere [Mathematical Models of Global and Regional Processes in the Biosphere]. / A.M. Tarko // Obshhaja i prikladnaja cenologija [General and Applied Biocenology]. № 6, 2007, pp. 44-47. [in Russian]
3. Tarko A.M. Antropogennye izmenenija global'nyh biosfernyh processov. Matematicheskoe modelirovanie: monografija [Anthropogenic Changes in Global Biospheric Processes. Mathematical Modeling: Monograph] / A.M. Tarko - M.: Fizmatlit, 2005. - p. 232 [in Russian]
4. Parhomenko V.P. Global'naja klimaticheskaja model' s uchetom biogeohimicheskogo uglerodnogo cikla rastitel'nosti sushi [Global Climate Model Taking Into Account the Biogeochemical Carbon Cycle of Land Vegetation]. / V.P. Parhomenko // Matematicheskoe modelirovanie i chislennye metody [Mathematical Modeling and Numerical Methods], 2021, № 2, 38–53. [in Russian]
5. Parhomenko V.P. Organizacija chislennyh jeksperimentov na modeli obshhej cirkuljacii atmosfery i global'noj modeli okeana [Organization of Numerical Experiments on the General Atmospheric Circulation Model and the Global Ocean Model]. / V.P. Parhomenko // Zhurnal vychislitel'noj matematiki i matematicheskoj fiziki [Journal of Computational Mathematics and Mathematical Physics] 2021, Vol. 61, No. 10, pp. 1693–1703. [in Russian]
6. Tolstyh M.A. Modeli global'noj atmosfery i mirovogo okeana: algoritmy i superkomp'juternye tehnologii [Models of the Global Atmosphere and the World Ocean: Algorithms and Supercomputer Technologies]. / M.A. Tolstyh, R.A. Ibraev et al. - M: Publishing house MGU, 2013. p. 144 [in Russian]
7. Pedloski Dzh. Geofizicheskaja gidrodinamika [Geophysical Hydrodynamics], Vol.1 / Dzh. Pedloski. - M.: Mir, 1984. - p. 398 [in Russian]
8. Parhomenko V. P. Primenenie global'nyh klimaticheskih modelej dlja issledovanija klimata Zemli [Application of Global Climate Models for the Study of the Earth’s Climate]. / V.P. Parhomenko // Trudy Instituta sistemnogo analiza Rossijskoj akademii nauk (Trudy ISA RAN) [Proceedings of the Institute of System Analysis of the Russian Academy of Sciences]. – 2018. – Vol. 68, №2. – pp. 38–41. [in Russian]
9. P. Parkhomenko Modeling of global and regional climate response to solar radiation management/ Parkhomenko V.P. // IOP Journal of Physics: Conference Series. – 2018 – V.1141, 012057. – P. 1-5. DOI:10.1088/1742-6596/1141/1/012057
10. Shepherd J. G. Overcoming the CFL time-step limitation: a stable iterative implicit numerical scheme for slowly evolving advection-diffusion systems // Ocean Modelling. 2002. V.4. P. 17-28.