GENERATION OF MAGNETIC FIELD IN THE ROTATING METALLIC CONDUCTOR
Сокол-Кутыловский О.Л.
Доктор технических наук, Институт геофизики Уральского отделения Российской Академии наук
ГЕНЕРАЦИЯ МАГНИТНОГО ПОЛЯ ВО ВРАЩАЮЩЕМСЯ МЕТАЛЛИЧЕСКОМ ПРОВОДНИКЕ
Аннотация
Показано, что вращающийся во внешнем магнитном поле металлический немагнитный проводник (в форме полого цилиндра) генерирует вторичное мультипольное магнитное поле, величина которого пропорциональна скорости вращения и величине первичного магнитного поля, а также зависит от удельного электрического сопротивления вращающегося проводника, его формы и размеров.
Ключевые слова: магнитное поле, сила Лоренца, генерация мультипольного магнитного поля.
Sokol-Kutylovskii O.L.
PhD in Engineering, Institute of Geophysics of Ural Branch of the Russian Academy of Sciences
GENERATION OF MAGNETIC FIELD IN THE ROTATING METALLIC CONDUCTOR
Abstract
It is shown that the non-magnetic metallic conductor (in the form of a hollow cylinder) which rotatates in external magnetic field generates a secondary multipole magnetic field which is proportional to the rotation speed and magnitude of the primary magnetic field, and also depends on the electrical resistivity of the rotating conductor of its shape and size.
Keywords: magnetic field, Lorentz force, the generation of the multipole magnetic field.
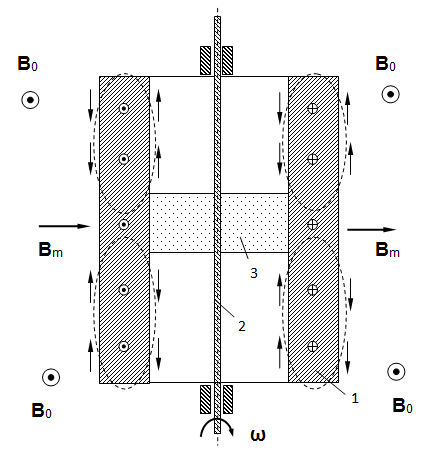
Известно, что постоянное магнитное поле возникает вокруг равномерно движущихся электрически заряженных частиц, например, вокруг проводника с электрическим током, а также создается ферро- и ферримагнетиками, в которых макроскопический магнитный момент обусловлен внутриатомными токами. А может ли возникнуть постоянное магнитное поле в немагнитном металлическом проводнике, через который не пропускают электрический ток? Простой эксперимент с вращением полого металлического немагнитного цилиндра во внешнем магнитном поле показывает, что в нем может возникнуть вторичное магнитное поле [1]. При скорости вращения алюминиевого полого цилиндра 60 радиан в секунду в постоянном магнитном поле ~1.6·10-4 Тл создается вторичное магнитное поле, ортогональное внешнему магнитному полю (Рис. 1). Вторичное поле по величине достигает ~10-4 Тл в центральной части цилиндра на расстоянии 5÷10 мм от его поверхности. Вращающийся алюминиевый цилиндр имел внешний диаметр 200 мм, длину 200 мм и толщину стенок 20 мм.
За эффект генерации вторичного магнитного поля ответственна сила Лоренца, действующая на электроны вращающегося проводника. Она вызывает в проводнике замкнутые циркулирующие электронные токи, генерирующие вторичное магнитное поле. В сечении цилиндра генерируемое вторичное магнитное поле является мультипольным, а вторичное магнитное поле всего проводника в целом – дипольное. Мультипольная структура генерируемого магнитного поля, наблюдаемая в поперечном сечении проводника, обусловлена его геометрической формой, определяющей пути течения электрических токов, создаваемых движением электронов под действием силы Лоренца, и распределением электрических потенциалов внутри проводника. В связи с такой структурой, генерируемое магнитное поле убывает с расстоянием от проводника значительно быстрее, чем поле классического магнитного диполя.
В общем случае величину максимальной магнитной индукции и направление максимального магнитного момента, генерируемого при вращении металлического немагнитного проводника во внешнем магнитном поле, можно оценить по формуле:
где Bm – максимальная магнитная индукция, генерируемая вращающимся проводником, km(σ, d) – коэффициент, зависящий от проводимости, формы и размеров проводника; B0 – внешнее постоянное магнитное поле и ω – вектор угловой скорости вращения проводника. Коэффициент km(σ,d) пропорционален проводимости, толщине и радиусу вращения проводника.
Рис. 1. Сечение вращающегося полого алюминиевого цилиндра 1, закрепленного на оси 2 через неметаллическую опору 3. B0 – внешнее постоянное магнитное поле, ω – вектор угловой скорости вращения, Bm – генерируемое суммарное магнитное поле. Стрелками показано направление магнитной индукции, генерируемой локальными токовыми диполями проводника. Мелкими кружками с точками и с крестами показано направление движения электронов при вращении проводника.
Величина генерируемой магнитной индукции, естественно, зависит от расстояния между вращающимся проводником и точкой измерения вторичной магнитной индукции. Разрезанный вдоль продольной оси полый металлический цилиндр сохраняет при вращении во внешнем магнитном поле способность к генерации вторичного магнитного поля.
Сплошной металлический цилиндрический проводник при вращении во внешнем магнитном поле также генерирует вторичное магнитное поле, но несколько меньшей величины, чем полый цилиндр. Полый проводящий цилиндр со стенками, навитыми из алюминиевой фольги, генерирует вторичное магнитное поле, величина которого прямо пропорциональна числу слоев фольги, то есть толщине проводника.
Таким образом, практически любой вращающийся во внешнем магнитном поле металлический немагнитный проводник генерирует вторичное магнитное поле, прямо пропорциональное внешнему постоянному магнитному полю и угловой скорости вращения. При этом сам вращающийся в магнитном поле (в том числе в магнитном поле Земли) проводник подобен униполярной электрической машине с короткозамкнутым ротором [2].
То, что эффект создается именно внешними, валентными электронами проводника следует из сильного влияния электронной проводимости материала вращающегося цилиндра на величину эффекта. Цилиндр из более проводящего металла создает большее по величине вторичное магнитное поле, чем цилиндр из менее проводящего металла или металлического сплава при прочих равных условиях (внешнее магнитное поле, частота вращения, размеры). По современным представлениям, электрическая проводимость пропорциональна средней длине свободного пробега электронов, которая в металлах и металлических сплавах превышает межатомные расстояния в тысячи раз. При этом считается, что на длине свободного пробега электроны ведут себя, подобно свободным частицам: они обладают инерцией, то есть стремятся сохранить имеющееся в данный момент состояние движения. На это прямо указывают опыты Стюарта и Толмена с торможением вращающихся катушек [3], а также инерционные свойства свободных электронов, проявляющиеся в электрическом токе самоиндукции [4]. На электроны могут оказывать влияние электромагнитные и гравитационные силы. Пример действия гравитационных сил – это работа униполярного индуктора, осуществляемая центробежной силой, действующей на внешние электроны вращающегося металлического проводника [3]. Эффект генерации вторичного магнитного поля в проводнике, вращающемся в магнитном поле, – это пример действия силы Лоренца на внешние электроны проводника, которые начинают перемещаться от одного атома к другому. Расстояние, проходимое электронами в непрерывном движении между атомами проводника соответствует длине свободного пробега, как если бы эти электроны были свободными. Большая длина свободного пробега электронов в проводниках –эффект, который наблюдается в металлах и металлических сплавах, когда их удельное электрическое сопротивление не превышает ~2×10-6 Ом×м [4]. При большем удельном электрическом сопротивлении проводника «длина свободного пробега» электронов равна расстоянию между соседними атомами, и в таком случае исчезает явление самоиндукции, прекращается работа униполярного генератора и генерация внутреннего магнитного поля вращающимся проводником.
Если внешнего магнитного поля нет, то и в этом случае вращающийся немагнитный проводник может генерировать собственное магнитное поле. В этом случае на свободные электроны проводника должна действовать другая, например, центробежная сила, как в униполярном индукторе. Для этого необходимо соединить центральный и периферийный участки быстро вращающегося проводника через токосъемные кольца. Другие силы инерции также способны привести электроны проводника в направленное движение и создать вокруг него магнитное поле. При торможении вращающихся проводников – это сила инерции вращательного движения (опыты Стюарта и Толмена), а при прямолинейном торможении – сила Ньютона.
Вторичное магнитное поле будет практически отсутствовать в тонком металлическом диске, ось которого совпадает с осью вращения, а вектор внешнего магнитного поля параллелен плоскости этого диска. При равномерном вращении такого наборного диска с изолированными элементами со скоростью до 200 оборотов в секунду величина вторичной магнитной индукции практически отсутствовала (с погрешностью ~10-6 от магнитной индукции внешнего поля) при ортогональном расположении оси вращения по отношению к вектору внешнего магнитного поля. Это показывает, что никаких других механизмов возбуждения вторичного магнитного поля, кроме как описанных выше, нет. В этом эксперименте действие силы Лоренца исключалась конструкцией вращающегося проводника. Вторичное магнитное поле также не возникает в разомкнутом (медном) соленоиде при его вращении вдоль продольной оси.
Наблюдаемая в этой простой динамической системе сложная структура магнитного поля может быть тем звеном, которое поможет понять причину возникновения макроскопического магнитного момента в магнетиках.
Литература
- Сокол-Кутыловский О.Л. Эффект генерации мультипольного магнитного поля. //Практика приборостроения 2003, № 3, С. 85-88.
- Тамм И.Е. Основы теории электричества. 9 изд., М.: Наука, 1976. 504 с.
- Зисман Г.А., Тодес О.М. Курс общей физики. М.: Наука, 1969, т. 2. 366 с.
- Сокол-Кутыловский О.Л. Об электродинамике проводящих сред. // Практика приборостроения. 2003. № 2, С. 85-90.
References
- Sokol-Kutylovskij O.L. Jeffekt generacii mul'tipol'nogo magnitnogo polja. //Praktika priborostroenija 2003, № 3, S. 85-88.
- Tamm I.E. Osnovy teorii jelektrichestva. 9 izd., M.: Nauka, 1976. 504 s.
- Zisman G.A., Todes O.M. Kurs obshhej fiziki. M.: Nauka, 1969, t. 2. 366 s.
- Sokol-Kutylovskij O.L. Ob jelektrodinamike provodjashhih sred. // Praktika priborostroenija. 2003. № 2, S. 85-90.